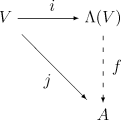Producto exterior
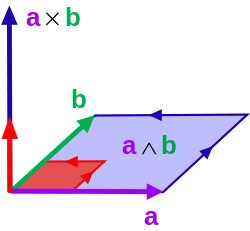
, que en tres dimensiones también se puede calcular usando el producto vectorial de los dos vectores.
Nótese que el coeficiente en esta última expresión es precisamente el determinante de la matriz [v w].
El hecho de que este coeficiente sea el área con signo no es algo accidental.
El producto cruzado u × v se puede interpretar como un vector que es perpendicular tanto a u como a v y cuya magnitud es igual al área del paralelogramo determinada por los dos vectores.
También se puede interpretar como el vector formado por el menor de la matriz con las columnas u y v.
El producto triple de u, v y w es un escalar con signo que representa un volumen con orientación geométrica.
Algebraicamente, es el determinante de la matriz con columnas u, v y w. El producto exterior en tres dimensiones permite interpretaciones similares: también se puede identificar con longitudes orientadas, áreas, volúmenes, etc., que están atravesados por uno, dos o más vectores.
El coeficiente binomial produce el resultado correcto, incluso en casos excepcionales; en particular, Λk(V) = { 0 } para k > n .
Cualquier elemento del álgebra exterior se puede escribir como una suma de k-vectores.
Por lo tanto, si ei es una base para V, entonces α se puede expresar únicamente como donde aij = −aji (la matriz de coeficientes es antisimétrica).
Las álgebras exteriores de fibrado vectorial se consideran con frecuencia en geometría y topología.
Esto se extiende por linealidad y homogeneidad a una operación, también denotada por Alt, en el álgebra tensorial completa T(V).
La discusión anterior se especializa en el caso de X = K, la base del campo.
Si V es de dimensión finita, entonces este último es naturalmente isomorfo a Λk( V∗).
Bajo esta identificación, el producto exterior toma una forma concreta: produce una nueva aplicación antisimétrica a partir de otras dos dadas.
Si V∗ denota el espacio dual al espacio vectorial V, entonces para cada α ∈ V∗, es posible definir una antiderivación en el álgebra Λ (V), Esta derivación se llama el producto interno con α, o algunas veces el operador de inserción, o la contracción por α. Supóngase que w ∈ ΛkV.
Entonces w es una aplicación multilineal de V∗ sobre K, por lo que está definido por sus valores en la k-hoja del producto cartesiano V∗ × V∗ × ... × V∗.
Esto luego se extiende bilinealmente (o sesquilinearmente en el caso complejo) a un producto interior no degenerado en ΛkV.
Esta definición del coproducto se eleva al espacio completo Λ(V) por homomorfismo (lineal).
Extendiéndose al espacio completo Λ (V), se tiene que El símbolo tensorial ⊗ utilizado en esta sección debe entenderse con cierta precaución: "no" es el mismo símbolo tensorial que se utiliza en la definición del producto alterno.
Se puede construir un producto alterno a partir de ⊗, entendiendo que funciona en un espacio diferente.
En términos del coproducto, el producto exterior en el espacio dual es solo el dual graduado del coproducto: donde el producto tensorial en el lado derecho es de aplicaciones lineales multilineales (extendido por cero en elementos de grado homogéneo incompatible: más precisamente, α ∧ β = ε ∘ (α ⊗ β) ∘ Δ, donde ε es el contador, como se define actualmente).
Entonces, por la propiedad universal, existe un homomorfismo único de álgebras graduadas tal que En particular, Λ(f) conserva el grado homogéneo.
Esto sugiere que el determinante se puede definir en términos del producto exterior de los vectores columna.
La derivada exterior conmuta con el regrediente en aplicaciones diferenciables entre múltiples, y por lo tanto, es un operador diferencial natural.
El álgebra exterior sobre los números complejos es el ejemplo arquetípico de una superálgebra, que juega un papel fundamental en las teorías físicas pertenecientes a los fermiones y la supersimetría.
Un solo elemento del álgebra exterior se llama supernúmero[22] o número de Grassmann.
Saint-Venant también publicó ideas similares de cálculo exterior por las que reclamó la prioridad sobre Grassmann.
Por lo tanto, era un cálculo, muy parecido a la lógica proposicional, excepto en que se enfocaba exclusivamente en la tarea del razonamiento formal en términos geométricos.
Poco tiempo después, Alfred North Whitehead, tomando prestadas las ideas de Peano y Grassmann, presentó su álgebra universal.