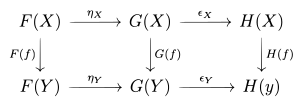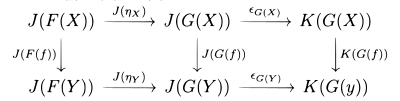Transformación natural
Por lo tanto, una transformación natural se puede considerar como un morfismo de funtores.
Si F y G son funtores (covariantes) entre las categorías C y D, entonces una transformación natural η de F a G asocia a cada objeto X en C un morfismo ηX : F(X) → G(X) en D, tal que para cada morfismo f : X → Y en C se tiene que Esta ecuación se puede expresar convenientemente por el diagrama conmutativo
Si η es una transformación natural de F a G, se escribe también η: F → G. Si, para cada objeto X en C, el morfismo ηX es un isomorfismo en D, entonces η se dice un isomorfismo natural (o a veces una equivalencia natural o isomorfismo de funtores).
Ahora se va a dar el significado exacto de esta declaración así como su demostración.
Si (G,*) es un grupo, se define su grupo opuesto (Gop, *op) como sigue: Gop es el mismo conjunto que G, y la operación *op es definida por a*opb = b*a.
, porque cualquier homomorfismo en un grupo abeliano elimina al subgrupo del conmutador.
Los functores y las transformaciones naturales abundan en topología algebraica, siendo los homomorfismos de Hurewicz un ejemplo.
debido a que el determinante está definido por la misma fórmula para cada anillo,
Estas aplicaciones son "naturales" en el siguiente sentido: la operación dual doble es un funtor, y las aplicaciones son los componentes de una transformación natural del funtor identidad al functor dual doble.
, que no debe confundirse con el funtor grupo opuesto trivial en
Además, cada par de funtores adjuntos viene equipado con dos transformaciones naturales (generalmente no isomorfismos) llamadas unidad y counidad.
De manera informal, una aplicación particular (especialmente un isomorfismo) entre objetos individuales (no categorías completas) se denomina isomorfismo natural, lo que significa implícitamente que en realidad está definido en toda la categoría y define una transformación natural de funtores.
Por el contrario, una aplicación particular entre objetos particulares puede denominarse isomorfismo antinatural (o "un isomorfismo que no es natural") si la aplicación no puede extenderse a una transformación natural en toda la categoría.
la prueba de antinaturalidad se muestra más fácilmente dando un automorfismo
con el isomorfismo dado por la proyección sobre los dos factores, fundamentalmente porque las aplicaciones en un espacio de productos son exactamente productos de las aplicaciones en los componentes, lo que constituye una declaración funtorial.
Sin embargo, el toro (que es abstractamente un producto de dos círculos) tiene un grupo fundamental isomorfo a
Sin embargo, si se da el toro como el producto
La naturalidad es una noción categórica y requiere ser muy preciso acerca de qué datos se dan exactamente: el toro como un espacio que resulta ser un producto (en la categoría de espacios y aplicaciones continuos) es diferente del toro presentado como un producto (en la categoría de productos de dos espacios y aplicaciones continuas entre los respectivos componentes).
[2] Sin embargo, las categorías relacionadas (con estructura adicional y restricciones en las aplicaciones) tienen un isomorfismo natural, como se describe a continuación.
Intuitivamente esto se debe a que requirió una elección, rigurosamente porque "cualquier" elección de isomorfismos no conmutará con, por ejemplo, la aplicación cero (consúltese (Mac Lane y Birkhoff, 1999, §VI.4) para una discusión detallada).
A partir de espacios vectoriales de dimensión finita (como objetos) y los funtores identidad y duales, se puede definir un isomorfismo natural, pero esto requiere primero agregar una estructura adicional y luego restringir las aplicaciones de "todos las aplicaciones lineales" a "aplicaciones lineales que respeten este estructura".
Explícitamente, para cada espacio vectorial, se requiere que venga con los datos de un isomorfismo a su dual,
En otras palabras, se toman como objetos espacios vectoriales con una forma bilineal no degenerada
Vista desde esta perspectiva, esta construcción (agregar transformaciones para cada objeto, restringir aplicaciones para conmutar con ellos) es completamente general y no depende de ninguna propiedad particular de los espacios vectoriales.
A menudo, por razones de interés geométrico, esto se especializa en una subcategoría, al requerir que las formas bilineales no degeneradas tengan propiedades adicionales, como ser simétricas (matriz ortogonal), simétricas y definidas positivas (espacio producto interior), sesquilineales simétricas (espacios hermíticos), o antisimétricas y totalmente isotrópicas (espacio vectorial simpléctico entre otras).
En todas estas categorías un espacio vectorial se identifica naturalmente con su dual, por la forma bilineal no degenerada.
con componentes Usando el bigoteo (véase más abajo), se puede escribir por eso Esta composición horizontal de transformaciones naturales también es asociativa con la identidad, que es a su vez la transformación natural de identidad sobre el funtor, es decir, la transformación natural que asocia a cada objeto su morfismo: para el objeto
) generalmente no es la identidad izquierda (respectivamente, derecha) de la composición horizontal
sin tener que analizar componentes y el diagrama conmutativo: Si
Cada límite y colímite proporciona un ejemplo de una transformación natural simple, ya que un cono equivale a una transformación natural con un funtor diagonal como dominio.