Integración
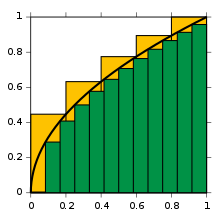
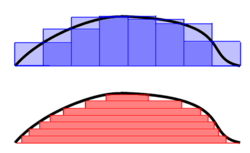
Los principios de la integración fueron formulados por Newton y Leibniz a finales del siglo XVII.Las integrales y las derivadas pasaron a ser herramientas básicas del cálculo, con numerosas aplicaciones en ciencia e ingeniería.Más tarde, Zu Chongzhi usó este método para encontrar el volumen de una esfera.En particular, el teorema fundamental del cálculo permite resolver una clase más amplia de problemas.También cabe destacar todo el marco estructural alrededor de la matemática que desarrollaron también Newton y Leibniz.El llamado cálculo infinitesimal permitió analizar, de forma precisa, funciones con dominios continuos.Posteriormente, este marco ha evolucionado hacia el cálculo moderno, cuya notación para las integrales procede directamente del trabajo de Leibniz.Es memorable la expresión del obispo Berkeley interpretando los infinitesimales como los «fantasmas de las cantidades que se desvanecen».[2][3] Para indicar summa (ſumma; en latín ‘suma’ o ‘total’), adaptó el símbolo integral, «∫», a partir de una letra S alargada porque consideraba a la integral como una suma infinita de addendas (‘sumandos’) infinitesimales.Tal como se puede inferir, el verdadero valor de la integral tendrá que ser más pequeño.Particionando la superficie en estudio, con trazos verticales, de tal manera que vamos obteniendo pequeños rectángulos, y reduciendo cada vez más el ancho de los rectángulos empleados para hacer la aproximación, se obtendrá un mejor resultado.Por ejemplo, dividamos el intervalo en cinco partes, empleando los puntos 0, 1⁄5, 2⁄5,3⁄5,4⁄5 y finalmente la abscisa 1.De este modo, el valor exacto del área bajo la curva se calcula formalmente como:La geometría diferencial, con su «cálculo de variedades», proporciona otra interpretación a esta notación familiar.Ahora f(x) y dx pasan a ser una forma diferencial, ω = f(x)dx, aparece un nuevo operador diferencial d, conocido como la derivada exterior, y el teorema fundamental pasa a ser el (más general) teorema de Stokes,Recientemente, los infinitesimales han reaparecido con rigor, a través de innovaciones modernas como el análisis no estándar.Se establecen diferencias para poder abordar casos especiales que no pueden ser integrables con otras definiciones, pero también en ocasiones por razones pedagógicas.La integral de Darboux está definida como el único número acotado entre las sumas inferior y superior, es decir,Este es el enfoque que toma Bourbaki[18] y cierto número de otros autores.Una integral impropia aparece cuando una o más de estas condiciones no se satisface.En general, una integral sobre un conjunto E de una función f se escribe: Aquí x no hace falta que sea necesariamente un número real, sino que puede ser cualquier otra cantidad apropiada, por ejemplo, un vector de R3.Así, las integrales de superficie tienen aplicaciones en la física, en particular en la teoría clásica del electromagnetismo.Muy a menudo, es necesario emplear una de las muchas técnicas que se han desarrollado para evaluar integrales.En muchos problemas de matemática, física, e ingeniería en los que participa la integración es deseable tener una fórmula explícita para la integral.Con el desarrollo de los ordenadores, muchos profesionales, educadores y estudiantes han recurrido a los sistemas de cálculo algebraico por ordenador, que han sido diseñados específicamente para desarrollar tareas tediosas o difíciles, entre las cuales se encuentra la integración.Por desgracia, resulta que las funciones con expresiones cerradas para sus primitivas son la excepción en vez de ser la regla.Algunas integrales no se pueden hallar con exactitud, otras necesitan de funciones especiales que son muy complicadas de calcular, y otras son tan complejas que encontrar la respuesta exacta es demasiado lento.Esto motiva el estudio y la aplicación de métodos numéricos para aproximar integrales.Si se quiere saber la distancia que ha recorrido el cuerpo durante un tiempo dado T se puede razonar (empleando análisis no estándar) que en torno a cada instante t la velocidad es constante salvo variaciones infinitesimales, por lo tanto el espacio recorrido en este instante durante un periodo de tiempo infinitesimal dt es v(t)dt, la suma de todos los espacios recorridos durante todos los instantes desde t=0 hasta t=T (el momento en que se quiere saber la distancia recorrida) y se calcula con la integral: El resultado de esta integral es: Otros ejemplos de campos de la física donde se aplican las integrales: El cálculo fraccional de conjuntos (Fractional Calculus of Sets (FCS)), mencionado por primera vez en el artículo titulado "Sets of Fractional Operators and Numerical Estimation of the Order of Convergence of a Family of Fractional Fixed-Point Methods",[7] es una metodología derivada del cálculo fraccional.En ese momento, Leibniz no pudo proporcionar una interpretación física o geométrica para esta pregunta, por lo que simplemente respondió a L’Hopital en una carta que "... es una aparente paradoja de la cual, algún día, se derivarán consecuencias útiles".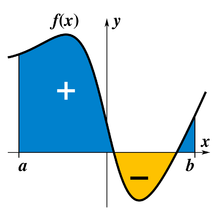




tiene intervalos no acotados tanto en el dominio como en el recorrido.

no está acotada internamente, pero ambos límites (por la derecha y por la izquierda) existen.








![{\displaystyle \int _{-1}^{1}{\frac {{\text{d}}x}{\sqrt[{3}]{x^{2}}}}=6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9cc2a98d964ffec675a749da1265f94b5596015)

