Intervalo (matemática)
[2] Es un conjunto medible y tiene la misma cardinalidad que la recta real.
que verifica la siguiente propiedad: Si
Existen dos notaciones principales: en un caso se utilizan corchetes y corchetes invertidos, en el otro corchetes y paréntesis; ambas notaciones están descritas en el estándar internacional ISO 31-11.
llamado intervalo abierto de extremo inferior
es el conjunto de números reales comprendidos entre
: este conjunto no contiene a ninguno de los extremos
es igual a su interior, su frontera es el conjunto
En notación conjuntista: Incluye únicamente uno de los extremos.
En notación conjuntista: En notación conjuntista: Los cuatro tipos de intervalos anteriores se llaman finitos; los expertos asignan como su longitud
Son muy útiles en el análisis matemático y en los temas de topología general, para el estudio de diferentes conceptos como clausura, interior, frontera, conexidad, etc.[7] Se usan en definición de funciones como la función máximo entero, o la función techo o función piso en matemáticas discretas y para la solución de ecuaciones que conllevan valor absoluto, la función signo, etc.[8] Los intervalos finitos tienen un centro de simetría que es
, no existe punto medio y el intervalo abierto es
[9] Este tipo de intervalos aparece cuando se conoce solo uno de los extremos y el otro es el infinito, es decir, un valor en términos absolutos mayor que cualquier otro, ya sea positivo o negativo.
Al no poderse incluir el infinito en el intervalo, estos se consideran siempre abiertos.
Incluye un extremo e infinito por la derecha.
es el conjunto de todos los números reales
es el conjunto de todos los números reales
sería: Un elemento está en la unión de dos o más conjuntos si y solo si está por lo menos en uno de ellos.
Se nota de la siguiente manera:
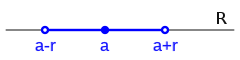
Partiendo del concepto de intervalo, podemos definir el entorno de un punto como el espacio que rodea a ese punto.
se representa: Un entorno reducido de centro
se representa: Un entorno reducido de un punto
Se pueden clasificar los intervalos según sus características topológicas (intervalos abiertos, cerrados, semiabiertos) o según sus características métricas (longitud: nula, finita no nula, infinita).
La siguiente tabla resume los 11 casos posibles, con
perteneciente al intervalo: [11] El número real
es el interior del intervalo cerrado de extremos
; y estos puntos son los únicos que están en la frontera del intervalo cerrado
; este es un conjunto cerrado y compacto con la topología usual de la recta .
a + c ≤ x + y ≤ b + d
usual los intervalos son las bolas abiertas y cerradas.
, al conjunto de puntos cuya distancia a