Logaritmo

Función matemática, inversa de una función exponencial

Gráficos de funciones logarítmicas, con tres bases de uso común. Los puntos especiales log _b  b = 1 se indican con líneas de puntos y todas las curvas se cruzan en log _b  1 = 0 .

En matemáticas , el logaritmo es la función inversa a la exponenciación . Eso significa que el logaritmo de un número  x en base  b es el exponente al que se debe elevar b para producir x . Por ejemplo, dado que 1000 = 10 ³ , el logaritmo en base  10 de 1000 es 3 , o log ₁₀  (1000) = 3 . El logaritmo de x en base  b se denota como log _b  ( x ) , o sin paréntesis, log _b  x , o incluso sin la base explícita, log  x , cuando no es posible confusión, o cuando la base no importa, como en notación O grande .

El logaritmo en base 10 se llama logaritmo decimal o común y se usa comúnmente en ciencia e ingeniería. El logaritmo natural tiene como base el número  e ≈ 2,718 ; su uso está muy extendido en matemáticas y física , debido a su derivada muy simple . El logaritmo binario utiliza base 2 y se utiliza con frecuencia en informática .

Los logaritmos fueron introducidos por John Napier en 1614 como medio para simplificar los cálculos. ^[1] Fueron adoptados rápidamente por navegantes, científicos, ingenieros, topógrafos y otros para realizar cálculos de alta precisión con mayor facilidad. Usando tablas de logaritmos , los tediosos pasos de multiplicación de varios dígitos se pueden reemplazar por búsquedas en tablas y sumas más simples. Esto es posible porque el logaritmo de un producto es la suma de los logaritmos de los factores:

$${\displaystyle \log _{b}(xy)=\log _{b}x+\log _{b}y,}$$

bxyb ≠ 1regla de cálculoLeonhard Eulerfunción exponenciale^[2]

Las escalas logarítmicas reducen cantidades amplias a ámbitos más pequeños. Por ejemplo, el decibelio (dB) es una unidad utilizada para expresar proporciones como logaritmos , principalmente para la potencia y amplitud de la señal (de las cuales la presión sonora es un ejemplo común). En química, el pH es una medida logarítmica de la acidez de una solución acuosa . Los logaritmos son comunes en fórmulas científicas y en mediciones de la complejidad de algoritmos y de objetos geométricos llamados fractales . Ayudan a describir proporciones de frecuencia de intervalos musicales , aparecen en fórmulas que cuentan números primos o aproximan factoriales , informan algunos modelos en psicofísica y pueden ayudar en la contabilidad forense .

El concepto de logaritmo como inverso de la exponenciación se extiende también a otras estructuras matemáticas. Sin embargo, en entornos generales, el logaritmo tiende a ser una función de múltiples valores. Por ejemplo, el logaritmo complejo es la inversa multivaluada de la función exponencial compleja. De manera similar, el logaritmo discreto es el inverso multivaluado de la función exponencial en grupos finitos; tiene usos en criptografía de clave pública .

Motivación

La gráfica del logaritmo en base 2 cruza el eje x en x = 1 y pasa por los puntos (2, 1) , (4, 2) y (8, 3) , representando, por ejemplo, log ₂ (8) = 3 y 2 ³ = 8 . La gráfica se acerca arbitrariamente al eje y , pero no lo alcanza .

La suma , la multiplicación y la exponenciación son tres de las operaciones aritméticas más fundamentales. La inversa de la suma es la resta y la inversa de la multiplicación es la división . De manera similar, un logaritmo es la operación inversa de la exponenciación . La exponenciación es cuando un número b , la base , se eleva a cierta potencia y , el exponente , para dar un valor x ; esto se denota

$${\displaystyle b^{y}=x.}$$

238 ${\displaystyle 2^{3}=8.}$

El logaritmo de base b es la operación inversa, que proporciona la salida y a partir de la entrada x . Es decir, equivale a si b es un número real positivo . (Si b no es un número real positivo, se pueden definir tanto la exponenciación como el logaritmo, pero pueden tomar varios valores, lo que hace que las definiciones sean mucho más complicadas). ${\displaystyle y=\log _{b}x}$ ${\displaystyle x=b^{y}}$

Una de las principales motivaciones históricas para la introducción de logaritmos es la fórmula

$${\displaystyle \log _{b}(xy)=\log _{b}x+\log _{b}y,}$$

las tablas de logaritmos

Definición

Dado un número real positivo b tal que b ≠ 1 , el logaritmo de un número real positivo x con respecto a la base  b ^{[nb 1]} es el exponente por el cual b debe elevarse para obtener x . En otras palabras, el logaritmo de x en base  b es el único número real  y tal que . ^[3] ${\displaystyle b^{y}=x}$

El logaritmo se denota " log _b  x " (pronunciado como "el logaritmo de x en base  b ", "el logaritmo en base b de x ", o más comúnmente "el log, en base  b , de x ").

Una definición equivalente y más sucinta es que la función log _b es la función inversa a la función . ${\displaystyle x\mapsto b^{x}}$

Ejemplos

• Iniciar sesión ₂  16 = 4 , ya que 2 ⁴ = 2 × 2 × 2 × 2 = 16 .
• Los logaritmos también pueden ser negativos: ya que ${\textstyle \log _{2}\!{\frac {1}{2}}=-1}$ ${\textstyle 2^{-1}={\frac {1}{2^{1}}}={\frac {1}{2}}.}$
• log ₁₀  150 es aproximadamente 2,176, que se encuentra entre 2 y 3, así como 150 se encuentra entre 10 ² = 100 y 10 ³ = 1000 .
• Para cualquier base  b , log _b  b = 1 y log _b  1 = 0 , ya que b ¹ = b y b ⁰ = 1 , respectivamente.

Identidades logarítmicas

Varias fórmulas importantes, a veces llamadas identidades logarítmicas o leyes logarítmicas , relacionan los logaritmos entre sí. ^[4]

Producto, cociente, potencia y raíz.

El logaritmo de un producto es la suma de los logaritmos de los números que se multiplican; el logaritmo de la razón de dos números es la diferencia de los logaritmos. El logaritmo de la p -ésima potencia de un número es p  multiplicado por el logaritmo del número mismo; el logaritmo de una raíz p -ésima es el logaritmo del número dividido por p . La siguiente tabla enumera estas identidades con ejemplos. Cada una de las identidades se puede derivar después de sustituir las definiciones de logaritmos o en el lado izquierdo. ${\displaystyle x=b^{\,\log _{b}x}}$ ${\displaystyle y=b^{\,\log _{b}y}}$

Cambio de base

El logaritmo log _b  x se puede calcular a partir de los logaritmos de x y b con respecto a una base arbitraria  k usando la siguiente fórmula: ^{[nb 2]}

$${\displaystyle \log _{b}x={\frac {\log _{k}x}{\log _{k}b}}.}$$

Las calculadoras científicas típicas calculan los logaritmos en bases 10 y e . ^[5] Los logaritmos con respecto a cualquier base  b se pueden determinar utilizando cualquiera de estos dos logaritmos mediante la fórmula anterior:

$${\displaystyle \log _{b}x={\frac {\log _{10}x}{\log _{10}b}}={\frac {\log _{e}x}{\log _{e}b}}.}$$

Dado un número x y su logaritmo y = log _b  x con una base desconocida  b , la base viene dada por:

$${\displaystyle b=x^{\frac {1}{y}},}$$

lo cual se puede ver al llevar la ecuación definitoria a la potencia de ${\displaystyle x=b^{\,\log _{b}x}=b^{y}}$ ${\displaystyle {\tfrac {1}{y}}.}$

bases particulares

Gráficas superpuestas del logaritmo de bases. 1 /2, 2 y mi

Entre todas las opciones para la base, tres son particularmente comunes. Estos son b = 10 , b = e (la constante matemática irracional e ≈ 2,71828183 ) y b = 2 (el logaritmo binario ). En el análisis matemático , el logaritmo en base e está muy extendido debido a las propiedades analíticas que se explican a continuación. Por otro lado, los logaritmos de base 10 (el logaritmo común ) son fáciles de usar para cálculos manuales en el sistema numérico decimal : ^[6]

$${\displaystyle \ \log _{10}(\ 10\ x\ )\ =\ \log _{10}10\ +\ \log _{10}x\ =\ 1\ +\ \log _{10}x~.}$$

Por lo tanto, log ₁₀  ( x ) está relacionado con el número de dígitos decimales de un entero positivo x : El número de dígitos es el entero más pequeño estrictamente mayor que log ₁₀  ( x ) . ^[7] Por ejemplo, log ₁₀ (5986) es aproximadamente 3,78. El siguiente número entero encima es 4, que es el número de dígitos de 5986. Tanto el logaritmo natural como el logaritmo binario se utilizan en teoría de la información , correspondiendo al uso de nats o bits como unidades fundamentales de información, respectivamente. ^[8] Los logaritmos binarios también se utilizan en informática , donde el sistema binario es ubicuo; en teoría musical , donde una proporción de tono de dos (la octava ) es omnipresente y el número de centavos entre dos tonos cualesquiera es una versión escalada del logaritmo binario, o log 2 veces 1200, de la proporción de tono (es decir, 100 centavos por semitono en temperamento igual convencional ), o equivalentemente la base logarítmica 2 ^1/1200  ; y en fotografía los logaritmos de base 2 reescalados se utilizan para medir valores de exposición , niveles de luz , tiempos de exposición , aperturas de lentes y velocidades de película en "stops". ^[9]

Muchas disciplinas escriben log  x como abreviatura de log _b x cuando la base prevista se puede inferir en función del contexto o la disciplina (o cuando la base es indeterminada o inmaterial). En informática, log generalmente se refiere a log ₂ , y en matemáticas log generalmente se refiere a log _e . ^[10] En otros contextos, log a menudo significa log ₁₀ . ^[11] La siguiente tabla enumera notaciones comunes para logaritmos en estas bases y los campos donde se utilizan. La columna "Notación ISO" enumera las designaciones sugeridas por la Organización Internacional de Normalización . ^[12]  

Historia

La historia de los logaritmos en la Europa del siglo XVII vio el descubrimiento de una nueva función que extendió el ámbito del análisis más allá del alcance de los métodos algebraicos. El método de los logaritmos fue propuesto públicamente por John Napier en 1614, en un libro titulado Mirifici Logarithmorum Canonis Descriptio ( Descripción del maravilloso canon de los logaritmos ). ^{[19] [20]} Antes de la invención de Napier, habían existido otras técnicas de alcance similar, como la prosthaféresis o el uso de tablas de progresiones, ampliamente desarrolladas por Jost Bürgi alrededor de 1600. ^{[21] [22]} Napier acuñó el término para logaritmo en latín medio, "logaritmo", derivado del griego, que literalmente significa "relación-número", de logos "proporción, relación, palabra" + arithmos "número".

El logaritmo común de un número es el índice de la potencia de diez que es igual al número. ^[23] Hablar de que un número requiere tantas cifras es una alusión aproximada al logaritmo común, y Arquímedes se refirió a él como el "orden de un número". ^[24] Los primeros logaritmos reales fueron métodos heurísticos para convertir la multiplicación en suma, facilitando así el cálculo rápido. Algunos de estos métodos utilizaron tablas derivadas de identidades trigonométricas. ^[25] Estos métodos se denominan prosthaféresis .

La invención de la función ahora conocida como logaritmo natural comenzó como un intento de realizar una cuadratura de una hipérbola rectangular por parte de Grégoire de Saint-Vincent , un jesuita belga que residía en Praga. Arquímedes había escrito La cuadratura de la parábola en el siglo III a. C., pero una cuadratura de la hipérbola eludió todos los esfuerzos hasta que Saint-Vincent publicó sus resultados en 1647. La relación que proporciona el logaritmo entre una progresión geométrica en su argumento y una progresión aritmética de valores, impulsó a AA de Sarasa a relacionar la cuadratura de Saint-Vincent y la tradición de los logaritmos en la prostaféresis , dando lugar al término "logaritmo hiperbólico", sinónimo de logaritmo natural. Pronto la nueva función fue apreciada por Christiaan Huygens y James Gregory . La notación Log y fue adoptada por Leibniz en 1675, ^[26] y al año siguiente la conectó a la integral ${\textstyle \int {\frac {dy}{y}}.}$

Antes de que Euler desarrollara su concepción moderna de los logaritmos naturales complejos, Roger Cotes obtuvo un resultado casi equivalente cuando demostró en 1714 que ^[27]

$${\displaystyle \log(\cos \theta +i\sin \theta )=i\theta .}$$

Tablas de logaritmos, reglas de cálculo y aplicaciones históricas.

La explicación de los logaritmos de la Encyclopædia Britannica de 1797

Al simplificar cálculos difíciles antes de que estuvieran disponibles las calculadoras y las computadoras, los logaritmos contribuyeron al avance de la ciencia, especialmente de la astronomía . Fueron fundamentales para los avances en topografía , navegación celeste y otros dominios. Pierre-Simon Laplace llamó logaritmos

"...[un] artificio admirable que, al reducir a unos pocos días el trabajo de muchos meses, duplica la vida del astrónomo y le ahorra los errores y disgustos inseparables de los largos cálculos." ^[28]

Como la función f ( x ) = b ^x es la función inversa de log _b  x , se la ha llamado antilogaritmo . ^[29] Hoy en día, esta función se denomina más comúnmente función exponencial .

Tablas de registro

Una herramienta clave que permitió el uso práctico de los logaritmos fue la tabla de logaritmos . ^[30] La primera tabla de este tipo fue compilada por Henry Briggs en 1617, inmediatamente después de la invención de Napier pero con la innovación de utilizar 10 como base. La primera tabla de Briggs contenía los logaritmos comunes de todos los números enteros en el rango de 1 a 1000, con una precisión de 14 dígitos. Posteriormente se redactaron tablas de alcance creciente. Estas tablas enumeraban los valores de log ₁₀  x para cualquier número  x en un rango determinado, con cierta precisión. Los logaritmos de base 10 se utilizaron universalmente para el cálculo, de ahí el nombre de logaritmo común, ya que los números que difieren en factores de 10 tienen logaritmos que difieren en números enteros. El logaritmo común de x se puede separar en una parte entera y una parte fraccionaria , conocida como característica y mantisa . Las tablas de logaritmos solo necesitan incluir la mantisa, ya que la característica se puede determinar fácilmente contando dígitos desde el punto decimal. ^[31] La característica de 10 · x es uno más la característica de x , y sus mantisas son iguales. Así, utilizando una tabla logarítmica de tres dígitos, el logaritmo de 3542 se aproxima por

$${\displaystyle \log _{10}3542=\log _{10}(1000\cdot 3.542)=3+\log _{10}3.542\approx 3+\log _{10}3.54}$$

Se puede obtener una mayor precisión mediante la interpolación :

$${\displaystyle \log _{10}3542\approx 3+\log _{10}3.54+0.2(\log _{10}3.55-\log _{10}3.54)}$$

El valor de 10 ^x se puede determinar mediante búsqueda inversa en la misma tabla, ya que el logaritmo es una función monótona .

Cálculos

El producto y el cociente de dos números positivos cyd se calculaban habitualmente como la suma y la diferencia de sus logaritmos. El producto  cd o cociente  c / d surgió de buscar el antilogaritmo de la suma o diferencia, mediante la misma tabla:

$${\displaystyle cd=10^{\,\log _{10}c}\,10^{\,\log _{10}d}=10^{\,\log _{10}c\,+\,\log _{10}d}}$$

$${\displaystyle {\frac {c}{d}}=cd^{-1}=10^{\,\log _{10}c\,-\,\log _{10}d}.}$$

Para cálculos manuales que exigen una precisión apreciable, realizar las búsquedas de los dos logaritmos, calcular su suma o diferencia y buscar el antilogaritmo es mucho más rápido que realizar la multiplicación mediante métodos anteriores como la prostaféresis , que se basa en identidades trigonométricas .

Los cálculos de potencias y raíces se reducen a multiplicaciones o divisiones y búsquedas por

$${\displaystyle c^{d}=\left(10^{\,\log _{10}c}\right)^{d}=10^{\,d\log _{10}c}}$$

y

$${\displaystyle {\sqrt[{d}]{c}}=c^{\frac {1}{d}}=10^{{\frac {1}{d}}\log _{10}c}.}$$

Los cálculos trigonométricos fueron facilitados por tablas que contenían los logaritmos comunes de las funciones trigonométricas .

Las reglas de cálculo

Otra aplicación crítica fue la regla de cálculo , un par de escalas divididas logarítmicamente que se utilizan para el cálculo. La escala logarítmica no móvil, la regla de Gunter , se inventó poco después de la invención de Napier. William Oughtred la mejoró para crear la regla de cálculo: un par de escalas logarítmicas que se pueden mover entre sí. Los números se colocan en escalas móviles a distancias proporcionales a las diferencias entre sus logaritmos. Deslizar la escala superior de manera apropiada equivale a sumar logaritmos mecánicamente, como se ilustra aquí:

Representación esquemática de una regla de cálculo. Comenzando desde 2 en la escala inferior, suma la distancia hasta 3 en la escala superior para llegar al producto 6. La regla de cálculo funciona porque está marcada de manera que la distancia de 1 a x es proporcional al logaritmo de x .

Por ejemplo, sumando la distancia de 1 a 2 en la escala inferior a la distancia de 1 a 3 en la escala superior se obtiene un producto de 6, que se lee en la parte inferior. La regla de cálculo fue una herramienta de cálculo esencial para ingenieros y científicos hasta la década de 1970, porque permite, a expensas de la precisión, un cálculo mucho más rápido que las técnicas basadas en tablas. ^[32]

Propiedades analíticas

Un estudio más profundo de los logaritmos requiere el concepto de función . Una función es una regla que, dado un número, produce otro número. ^[33] Un ejemplo es la función que produce la x -ésima potencia de b a partir de cualquier número real  x , donde la base  b es un número fijo. Esta función se escribe como f ( x ) = b ^x . Cuando b es positivo y desigual a 1, mostramos a continuación que f es invertible cuando se considera una función de los reales a los reales positivos.

Existencia

Sea b un número real positivo distinto de 1 y sea f ( x ) = b ^x .

Es un resultado estándar en el análisis real que cualquier función continua estrictamente monótona es biyectiva entre su dominio y rango. Este hecho se deriva del teorema del valor intermedio . ^[34] Ahora, f es estrictamente creciente (para b > 1 ), o estrictamente decreciente (para 0 < b < 1 ), ^[35] es continua, tiene dominio y rango . Por tanto, f es una biyección de a . En otras palabras, por cada número real positivo y , hay exactamente un número real x tal que . ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} _{>0}}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} _{>0}}$ ${\displaystyle b^{x}=y}$

Denotemos la inversa de f . Es decir, log _b y es el único número real x tal que . Esta función se llama función logarítmica en base b o función logarítmica (o simplemente logaritmo ). ${\displaystyle \log _{b}\colon \mathbb {R} _{>0}\to \mathbb {R} }$  ${\displaystyle b^{x}=y}$

Caracterización por la fórmula del producto.

La función log _b  x también se puede caracterizar esencialmente mediante la fórmula del producto

$${\displaystyle \log _{b}(xy)=\log _{b}x+\log _{b}y.}$$

b > 1función creciente ff ( b ) = 1^[36]

$${\displaystyle f(xy)=f(x)+f(y).}$$

Gráfica de la función logaritmo

La gráfica de la función logaritmo log _b  ( x ) (azul) se obtiene reflejando la gráfica de la función b ^x (roja) en la línea diagonal ( x = y ).

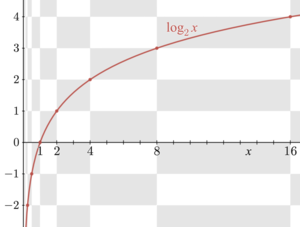
Como se analizó anteriormente, la función log _b es la inversa de la función exponencial . Por lo tanto, sus gráficas se corresponden entre sí al intercambiar las coordenadas x e y (o al reflexionar en la línea diagonal x = y ), como se muestra a la derecha: un punto ( t , u = b ^t ) en la gráfica de f produce un punto ( u , t = log _b u ) en la gráfica del logaritmo y viceversa. Como consecuencia, log _b  ( x ) diverge hasta el infinito (se hace más grande que cualquier número dado) si x crece hasta el infinito, siempre que b sea mayor que uno. En ese caso, log _b ( x ) es una función creciente . Para b < 1 , log _b  ( x ) tiende a menos infinito. Cuando x se acerca a cero, log _b x va a menos infinito para b > 1 (más infinito para b < 1 , respectivamente). ${\displaystyle x\mapsto b^{x}}$   

Derivada y antiderivada

La gráfica del logaritmo natural (verde) y su tangente en x = 1,5 (negro)

Las propiedades analíticas de las funciones pasan a sus inversas. ^[34] Por lo tanto, como f ( x ) = b x ^es una función continua y diferenciable , también lo es log _by  . En términos generales, una función continua es derivable si su gráfica no tiene "esquinas" agudas. Además, como la derivada de f ( x ) se evalúa como ln( b ) b ^x según las propiedades de la función exponencial , la regla de la cadena implica que la derivada de log _b  x viene dada por ^{[35] [37]}

$${\displaystyle {\frac {d}{dx}}\log _{b}x={\frac {1}{x\ln b}}.}$$

pendientetangenteen base b( x , log _b  ( x ))1/( x  ln( b ))

La derivada de ln( x ) es 1/ x ; esto implica que ln( x ) es la antiderivada única de 1/ x que tiene el valor 0 para x = 1 . Es esta fórmula tan sencilla la que motivó a calificar como “natural” al logaritmo neperiano; Esta es también una de las principales razones de la importancia de la constante  e .

La derivada con un argumento funcional generalizado f ( x ) es

$${\displaystyle {\frac {d}{dx}}\ln f(x)={\frac {f'(x)}{f(x)}}.}$$

derivada logarítmicaff' ( x )ln( f ( x ))diferenciación logarítmica^[38]logaritmo natural ln( x )^[39]

$${\displaystyle \int \ln(x)\,dx=x\ln(x)-x+C.}$$

A partir de esta ecuación se pueden derivar fórmulas relacionadas^[40]

Representación integral del logaritmo natural.

El logaritmo natural de t es el área sombreada debajo de la gráfica de la función f ( x ) = 1/ x (recíproco de x ).

El logaritmo natural de t se puede definir como la integral definida :

$${\displaystyle \ln t=\int _{1}^{t}{\frac {1}{x}}\,dx.}$$

ln( t )x1/ xx = 1x = tteorema fundamental del cálculoln( x )1/ x^[41]ln( tu ) = ln( t ) + ln( u )

$${\displaystyle \ln(tu)=\int _{1}^{tu}{\frac {1}{x}}\,dx\ {\stackrel {(1)}{=}}\int _{1}^{t}{\frac {1}{x}}\,dx+\int _{t}^{tu}{\frac {1}{x}}\,dx\ {\stackrel {(2)}{=}}\ln(t)+\int _{1}^{u}{\frac {1}{w}}\,dw=\ln(t)+\ln(u).}$$

La igualdad (1) divide la integral en dos partes, mientras que la igualdad (2) es un cambio de variable ( w = x / t ). En la siguiente ilustración, la división corresponde a dividir el área en las partes amarilla y azul. Cambiar la escala del área azul de la izquierda verticalmente por el factor  t y reducirla horizontalmente por el mismo factor no cambia su tamaño. Moviéndolo adecuadamente, el área se ajusta nuevamente a la gráfica de la función f ( x ) = 1/ x . Por lo tanto, el área azul de la izquierda, que es la integral de f ( x ) de t a tu, es la misma que la integral de 1 a u . Esto justifica la igualdad (2) con una demostración más geométrica.

Una prueba visual de la fórmula del producto del logaritmo natural.

La fórmula de potencia ln( t ^r ) = r ln( t ) se puede derivar de manera similar:

$${\displaystyle \ln(t^{r})=\int _{1}^{t^{r}}{\frac {1}{x}}dx=\int _{1}^{t}{\frac {1}{w^{r}}}\left(rw^{r-1}\,dw\right)=r\int _{1}^{t}{\frac {1}{w}}\,dw=r\ln(t).}$$

integración por sustituciónw = x ^{1/ r}

La suma de los recíprocos de los números naturales,

$${\displaystyle 1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}},}$$

serie armónicalogaritmo naturalninfinito

$${\displaystyle \sum _{k=1}^{n}{\frac {1}{k}}-\ln(n),}$$

convergeconstante de Euler-Mascheroni γ = 0,5772...Quicksort^[42]

Trascendencia del logaritmo

Los números reales que no son algebraicos se llaman trascendentales ; ^[43] por ejemplo, π y e son tales números, pero no lo son. Casi todos los números reales son trascendentales. El logaritmo es un ejemplo de función trascendental . El teorema de Gelfond-Schneider afirma que los logaritmos suelen tomar valores trascendentales, es decir, "difíciles". ^[44] ${\displaystyle {\sqrt {2-{\sqrt {3}}}}}$

Cálculo

Las teclas de logaritmo (LOG para base 10 y LN para base  e ) en una calculadora gráfica TI-83 Plus

Los logaritmos son fáciles de calcular en algunos casos, como log ₁₀  (1000) = 3 . En general, los logaritmos se pueden calcular utilizando series de potencias o la media aritmético-geométrica , o recuperarse de una tabla de logaritmos precalculada que proporciona una precisión fija. ^{[45] [46]} El método de Newton , un método iterativo para resolver ecuaciones de forma aproximada, también se puede utilizar para calcular el logaritmo, porque su función inversa, la función exponencial, se puede calcular de manera eficiente. ^[47] Usando tablas de búsqueda, se pueden usar métodos similares a CORDIC para calcular logaritmos usando solo las operaciones de suma y desplazamiento de bits . ^{[48] ​​[49]} Además, el algoritmo del logaritmo binario calcula lb( x ) de forma recursiva , basándose en elevaciones al cuadrado repetidas de x , aprovechando la relación

$${\displaystyle \log _{2}\left(x^{2}\right)=2\log _{2}|x|.}$$

Serie de potencia

serie de taylor

La serie de Taylor de ln( z ) centrada en z = 1 . La animación muestra las primeras 10 aproximaciones junto con la 99.ª y la 100.ª. Las aproximaciones no convergen más allá de una distancia de 1 del centro.

Para cualquier número real z que satisfaga 0 < z ≤ 2 , se cumple la siguiente fórmula: ^{[nb 5] [50]}

$${\displaystyle {\begin{aligned}\ln(z)&={\frac {(z-1)^{1}}{1}}-{\frac {(z-1)^{2}}{2}}+{\frac {(z-1)^{3}}{3}}-{\frac {(z-1)^{4}}{4}}+\cdots \\&=\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {(z-1)^{k}}{k}}.\end{aligned}}}$$

Equiparar la función ln( z ) con esta suma infinita ( serie ) es una abreviatura de decir que la función se puede aproximar a un valor cada vez más preciso mediante las siguientes expresiones (conocidas como sumas parciales ):

$${\displaystyle (z-1),\ \ (z-1)-{\frac {(z-1)^{2}}{2}},\ \ (z-1)-{\frac {(z-1)^{2}}{2}}+{\frac {(z-1)^{3}}{3}},\ \ldots }$$

Por ejemplo, con z = 1,5, la tercera aproximación produce 0,4167 , que es aproximadamente 0,011 mayor que ln(1,5) = 0,405465 , y la novena aproximación produce 0,40553 , que es sólo aproximadamente 0,0001 mayor. La n- ésima suma parcial puede aproximarse a ln( z ) con precisión arbitraria, siempre que el número de sumandos n sea lo suficientemente grande.

En cálculo elemental, se dice que la serie converge a la función ln( z ) , y la función es el límite de la serie. Es la serie de Taylor del logaritmo natural en z = 1 . La serie de Taylor de ln( z ) proporciona una aproximación particularmente útil a ln(1 + z ) cuando z es pequeño, | z | < 1 , desde entonces

$${\displaystyle \ln(1+z)=z-{\frac {z^{2}}{2}}+{\frac {z^{3}}{3}}-\cdots \approx z.}$$

Por ejemplo, con z = 0,1, la aproximación de primer orden da ln(1,1) ≈ 0,1 , que es menos del 5 % del valor correcto 0,0953 .

Tangente hiperbólica inversa

Otra serie se basa en la función tangente hiperbólica inversa :

$${\displaystyle \ln(z)=2\cdot \operatorname {artanh} \,{\frac {z-1}{z+1}}=2\left({\frac {z-1}{z+1}}+{\frac {1}{3}}{\left({\frac {z-1}{z+1}}\right)}^{3}+{\frac {1}{5}}{\left({\frac {z-1}{z+1}}\right)}^{5}+\cdots \right),}$$

z > 0^{[nb 6] [50]}notación sigma

$${\displaystyle \ln(z)=2\sum _{k=0}^{\infty }{\frac {1}{2k+1}}\left({\frac {z-1}{z+1}}\right)^{2k+1}.}$$

zz = 1,5a ln(1,5)3 × 10-6^​zy ≈ ln( z )

$${\displaystyle A={\frac {z}{\exp(y)}},}$$

z

$${\displaystyle \ln(z)=y+\ln(A).}$$

yAAserie exponencialyzzz = a · 10 ^bln( z ) = ln( a ) + b · ln(10)

Se puede utilizar un método estrechamente relacionado para calcular el logaritmo de números enteros. Poniendo en la serie anterior, se deduce que: ${\displaystyle \textstyle z={\frac {n+1}{n}}}$

$${\displaystyle \ln(n+1)=\ln(n)+2\sum _{k=0}^{\infty }{\frac {1}{2k+1}}\left({\frac {1}{2n+1}}\right)^{2k+1}.}$$

n , entonces esta serie produce una serie rápidamente convergente para log( n +1)tasa de convergencia ${\textstyle \left({\frac {1}{2n+1}}\right)^{2}}$

Aproximación de la media aritmético-geométrica

La media aritmético-geométrica produce aproximaciones de alta precisión del logaritmo natural . Sasaki y Kanada demostraron en 1982 que era particularmente rápido para precisiones entre 400 y 1000 decimales, mientras que los métodos de series de Taylor eran típicamente más rápidos cuando se necesitaba menos precisión. En su trabajo, ln( x ) se aproxima a una precisión de 2 ^{− p} (o p  bits precisos) mediante la siguiente fórmula (debida a Carl Friedrich Gauss ): ^{[51] [52]}

$${\displaystyle \ln(x)\approx {\frac {\pi }{2\,\mathrm {M} \!\left(1,2^{2-m}/x\right)}}-m\ln(2).}$$

Aquí M( x , y ) denota la media aritmético -geométrica de xey . Se obtiene calculando repetidamente el promedio ( x + y )/2 ( media aritmética ) y ( media geométrica ) de xey y luego permita que esos dos números se conviertan en los siguientes xey . Los dos números convergen rápidamente a un límite común que es el valor de M( x , y ) . m se elige tal que ${\textstyle {\sqrt {xy}}}$

$${\displaystyle x\,2^{m}>2^{p/2}.\,}$$

para asegurar la precisión requerida. Una m más grande hace que el cálculo de M( x , y ) tome más pasos (las x e y iniciales están más separadas, por lo que se necesitan más pasos para converger), pero brinda más precisión. Las constantes π y ln(2) se pueden calcular con series rápidamente convergentes.

algoritmo de feynman

Mientras trabajaba en el Laboratorio Nacional de Los Álamos en el Proyecto Manhattan , Richard Feynman desarrolló un algoritmo de procesamiento de bits para calcular el logaritmo que es similar a la división larga y que luego se utilizó en la Máquina de Conexión . El algoritmo se basa en el hecho de que todo número real x donde 1 < x < 2 puede representarse como un producto de distintos factores de la forma 1 + 2 ^{− k} . El algoritmo construye secuencialmente ese producto  P , comenzando con P = 1 y k = 1 : si P · (1 + 2 ^{− k} ) < x , entonces cambia P a P · (1 + 2 ^{− k} ) . Luego aumenta en uno independientemente. El algoritmo se detiene cuando k es lo suficientemente grande como para dar la precisión deseada. Debido a que log( x ) es la suma de los términos de la forma log(1 + 2 ^{− k} ) correspondientes a aquellos k para los cuales el factor 1 + 2 ^{− k} se incluyó en el producto  P , log( x ) puede calcularse mediante suma simple, usando una tabla de log(1 + 2 ^{− k} ) para todo k . Se puede utilizar cualquier base para la tabla de logaritmos. ^[53] ${\displaystyle k}$

Aplicaciones

Una concha de nautilo que muestra una espiral logarítmica.

Los logaritmos tienen muchas aplicaciones dentro y fuera de las matemáticas. Algunas de estas ocurrencias están relacionadas con la noción de invariancia de escala . Por ejemplo, cada cámara del caparazón de un nautilo es una copia aproximada de la siguiente, escalada por un factor constante. Esto da lugar a una espiral logarítmica . ^[54] La ley de Benford sobre la distribución de los dígitos principales también puede explicarse por la invariancia de escala. ^[55] Los logaritmos también están vinculados a la autosimilitud . Por ejemplo, los logaritmos aparecen en el análisis de algoritmos que resuelven un problema dividiéndolo en dos problemas más pequeños similares y parcheando sus soluciones. ^[56] Las dimensiones de formas geométricas autosemejantes, es decir, formas cuyas partes se parecen a la imagen general, también se basan en logaritmos. Las escalas logarítmicas son útiles para cuantificar el cambio relativo de un valor en comparación con su diferencia absoluta. Además, debido a que la función logarítmica log( x ) crece muy lentamente para x grandes , se utilizan escalas logarítmicas para comprimir datos científicos a gran escala. Los logaritmos también aparecen en numerosas fórmulas científicas, como la ecuación del cohete de Tsiolkovsky , la ecuación de Fenske o la ecuación de Nernst .

Escala logarítmica

Un gráfico logarítmico que representa el valor de un marco de oro en marcos de papel durante la hiperinflación alemana en la década de 1920.

Las cantidades científicas suelen expresarse como logaritmos de otras cantidades, utilizando una escala logarítmica . Por ejemplo, el decibelio es una unidad de medida asociada a cantidades en escala logarítmica . Se basa en el logaritmo común de relaciones : 10 veces el logaritmo común de una relación de potencia o 20 veces el logaritmo común de una relación de voltaje . Se utiliza para cuantificar la pérdida de niveles de voltaje en la transmisión de señales eléctricas, ^{[ cita necesaria ]} para describir los niveles de potencia de los sonidos en acústica , ^[57] y la absorbancia de la luz en los campos de la espectrometría y la óptica . La relación señal-ruido que describe la cantidad de ruido no deseado en relación con una señal (significativa) también se mide en decibelios. ^[58] De manera similar, la relación señal-ruido máxima se usa comúnmente para evaluar la calidad del sonido y los métodos de compresión de imágenes utilizando el logaritmo. ^[59]

La fuerza de un terremoto se mide tomando el logaritmo común de la energía emitida durante el terremoto. Esta se utiliza en la escala de magnitud de momento o escala de magnitud de Richter . Por ejemplo, un terremoto de 5,0 libera 32 veces (10 ^1,5 ) y uno de 6,0 libera 1000 veces (10 ³ ) la energía de un 4,0. ^[60] La magnitud aparente mide el brillo de las estrellas de forma logarítmica. ^[61] En química el negativo del logaritmo decimal, el decimalcologaritmo , se indica con la letra p.^[62]Por ejemplo,el pHes el cologaritmo decimal de laactividaddehidronio(la formaioneshidrógeno H ⁺
tomar agua). ^[63] La actividad de los iones hidronio en agua neutra es 10 ⁻⁷  mol·L ⁻¹ , por lo tanto un pH de 7. El vinagre normalmente tiene un pH de aproximadamente 3. La diferencia de 4 corresponde a una proporción de 10 ⁴ de la actividad , es decir, la actividad del ion hidronio del vinagre es de aproximadamente 10 ⁻³ mol·L ⁻¹ .

Los gráficos semilogarítmicos (log-lineales) utilizan el concepto de escala logarítmica para la visualización: un eje, normalmente el vertical, tiene una escala logarítmica. Por ejemplo, el gráfico de la derecha comprime el fuerte aumento de 1 millón a 1 billón en el mismo espacio (en el eje vertical) que el aumento de 1 a 1 millón. En tales gráficos, las funciones exponenciales de la forma f ( x ) = a · b ^x aparecen como líneas rectas con pendiente igual al logaritmo de b . Los gráficos log-log escalan ambos ejes logarítmicamente, lo que hace que las funciones de la forma f ( x ) = a · x ^k se representen como líneas rectas con pendiente igual al exponente  k . Esto se aplica en la visualización y análisis de leyes de potencia . ^[64]

Psicología

Los logaritmos aparecen en varias leyes que describen la percepción humana : ^{[65] [66]} La ley de Hick propone una relación logarítmica entre el tiempo que los individuos tardan en elegir una alternativa y el número de opciones que tienen. ^[67] La ​​ley de Fitts predice que el tiempo necesario para moverse rápidamente a un área objetivo es una función logarítmica de la distancia y el tamaño del objetivo. ^[68] En psicofísica , la ley de Weber-Fechner propone una relación logarítmica entre estímulo y sensación , como el peso real versus el percibido de un objeto que lleva una persona. ^[69] (Esta "ley", sin embargo, es menos realista que los modelos más recientes, como la ley de potencia de Stevens . ^[70] )

Los estudios psicológicos encontraron que las personas con poca educación matemática tienden a estimar cantidades logarítmicamente, es decir, colocan un número en una línea sin marcar según su logaritmo, de modo que 10 se ubica tan cerca de 100 como 100 lo está de 1000. El aumento de la educación cambia esto a una estimación lineal (colocando 1000 10 veces más lejos) en algunas circunstancias, mientras que los logaritmos se utilizan cuando los números que se van a representar son difíciles de trazar linealmente. ^{[71] [72]}

Teoría de probabilidad y estadística.

Tres funciones de densidad de probabilidad (PDF) de variables aleatorias con distribuciones log-normales. El parámetro de ubicación  μ , que es cero para las tres PDF mostradas, es la media del logaritmo de la variable aleatoria, no la media de la variable en sí.

Distribución de primeros dígitos (en %, barras rojas) en la población de los 237 países del mundo. Los puntos negros indican la distribución predicha por la ley de Benford.

Los logaritmos surgen en la teoría de la probabilidad : la ley de los grandes números dicta que, para una moneda justa , a medida que el número de lanzamientos aumenta hasta el infinito, la proporción observada de caras se acerca a la mitad . Las fluctuaciones de esta proporción alrededor de la mitad se describen mediante la ley del logaritmo iterado . ^[73]

Los logaritmos también ocurren en distribuciones log-normales . Cuando el logaritmo de una variable aleatoria tiene una distribución normal , se dice que la variable tiene una distribución log-normal. ^[74] Las distribuciones log-normales se encuentran en muchos campos, siempre que una variable se forma como producto de muchas variables aleatorias positivas independientes, por ejemplo en el estudio de la turbulencia. ^[75]

Los logaritmos se utilizan para la estimación de máxima verosimilitud de modelos estadísticos paramétricos . Para tal modelo, la función de verosimilitud depende de al menos un parámetro que debe estimarse. Un máximo de la función de verosimilitud ocurre en el mismo valor de parámetro que un máximo del logaritmo de la verosimilitud (el " logaritmo de verosimilitud "), porque el logaritmo es una función creciente. La probabilidad logarítmica es más fácil de maximizar, especialmente para las probabilidades multiplicadas de variables aleatorias independientes . ^[76]

La ley de Benford describe la aparición de dígitos en muchos conjuntos de datos , como las alturas de los edificios. Según la ley de Benford, la probabilidad de que el primer dígito decimal de un elemento en la muestra de datos sea d (de 1 a 9) es igual a log ₁₀  ( d + 1) − log ₁₀  ( d ) , independientemente de la unidad de medida. ^[77] Por lo tanto, se puede esperar que alrededor del 30% de los datos tengan 1 como primer dígito, el 18% comiencen con 2, etc. Los auditores examinan las desviaciones de la ley de Benford para detectar contabilidad fraudulenta. ^[78]

La transformación logarítmica es un tipo de transformación de datos que se utiliza para acercar la distribución empírica a la supuesta.

Complejidad computacional

El análisis de algoritmos es una rama de la informática que estudia el rendimiento de los algoritmos (programas informáticos que resuelven un determinado problema). ^[79] Los logaritmos son valiosos para describir algoritmos que dividen un problema en otros más pequeños y unen las soluciones de los subproblemas. ^[80]

Por ejemplo, para encontrar un número en una lista ordenada, el algoritmo de búsqueda binaria comprueba la entrada del medio y continúa con la mitad antes o después de la entrada del medio si aún no se encuentra el número. Este algoritmo requiere, en promedio, comparaciones log ₂  ( N ) , donde N es la longitud de la lista. ^[81] De manera similar, el algoritmo de ordenación por combinación ordena una lista sin ordenar dividiendo la lista en mitades y ordenándolas primero antes de fusionar los resultados. Los algoritmos de ordenación por fusión normalmente requieren un tiempo aproximadamente proporcional a N ·log( N ) . ^[82] La base del logaritmo no se especifica aquí, porque el resultado sólo cambia en un factor constante cuando se utiliza otra base. Un factor constante generalmente no se tiene en cuenta en el análisis de algoritmos según el modelo de costo uniforme estándar . ^[83]

Se dice que una función  f ( x ) crece logarítmicamente si f ( x ) es (exacta o aproximadamente) proporcional al logaritmo de x . (Sin embargo, las descripciones biológicas del crecimiento de los organismos utilizan este término para una función exponencial. ^[84] ) Por ejemplo, cualquier número natural  N puede representarse en forma binaria en no más de log ₂  N + 1  bits . En otras palabras, la cantidad de memoria necesaria para almacenar N crece logarítmicamente con N.

Entropía y caos

Billar sobre una mesa de billar ovalada . Dos partículas, que comienzan en el centro con un ángulo que difiere en un grado, toman caminos que divergen caóticamente debido a reflexiones en el límite.

La entropía es, en términos generales, una medida del desorden de algún sistema. En termodinámica estadística , la entropía  S de algún sistema físico se define como

$${\displaystyle S=-k\sum _{i}p_{i}\ln(p_{i}).\,}$$

ip _iikconstante de Boltzmannla entropía en la teoría de la informaciónlos Nlog ₂  N^[85]

Los exponentes de Lyapunov utilizan logaritmos para medir el grado de caticidad de un sistema dinámico . Por ejemplo, para una partícula que se mueve sobre una mesa de billar ovalada, incluso pequeños cambios en las condiciones iniciales dan como resultado trayectorias muy diferentes de la partícula. Estos sistemas son caóticos en un sentido determinista , porque pequeños errores de medición del estado inicial conducen, como era de esperar, a estados finales muy diferentes. ^[86] Al menos un exponente de Lyapunov de un sistema deterministamente caótico es positivo.

Fractales

El triángulo de Sierpinski (a la derecha) se construye reemplazando repetidamente triángulos equiláteros por tres más pequeños.

Los logaritmos aparecen en las definiciones de la dimensión de los fractales . ^[87] Los fractales son objetos geométricos que son autosemejantes en el sentido de que pequeñas partes reproducen, al menos aproximadamente, toda la estructura global. El triángulo de Sierpinski (en la foto) puede estar cubierto por tres copias de sí mismo, cada una de las cuales tiene lados la mitad de la longitud original. Esto hace que la dimensión de Hausdorff de esta estructura sea ln(3)/ln(2) ≈ 1,58 . Otra noción de dimensión basada en logaritmos se obtiene contando el número de casillas necesarias para cubrir el fractal en cuestión.

Música

Cuatro octavas diferentes mostradas en una escala lineal y luego en una escala logarítmica (a medida que el oído las escucha)

Los logaritmos están relacionados con los tonos e intervalos musicales . En temperamento igual , la relación de frecuencia depende sólo del intervalo entre dos tonos, no de la frecuencia específica o tono de los tonos individuales. Por ejemplo, la nota  La tiene una frecuencia de 440  Hz y la nota Si bemol tiene una frecuencia de 466 Hz. El intervalo entre La y Si bemol es un semitono , al igual que el que existe entre Si bemol y Si (frecuencia 493 Hz). En consecuencia, las relaciones de frecuencia coinciden:

$${\displaystyle {\frac {466}{440}}\approx {\frac {493}{466}}\approx 1.059\approx {\sqrt[{12}]{2}}.}$$

de base 2 ^1/12de frecuenciade base 2 ^1/1200centavos.^[88]

Teoría de los números

Los logaritmos naturales están muy ligados al conteo de números primos (2, 3, 5, 7, 11,...), un tema importante en la teoría de números . Para cualquier número entero  x , la cantidad de números primos menores o iguales a x se denota por π ( x ) . El teorema de los números primos afirma que π ( x ) está dado aproximadamente por

$${\displaystyle {\frac {x}{\ln(x)}},}$$

π ( x )x^[89]xproporcionalxπ ( x )integral logarítmica compensada Li( x )

$${\displaystyle \mathrm {Li} (x)=\int _{2}^{x}{\frac {1}{\ln(t)}}\,dt.}$$

hipótesis de Riemann , una de las conjeturasπ ( x )Li( x )^[90]teorema de Erdős-Kacfactores primoslogaritmo natural

El logaritmo de n factorial , n ! = 1 · 2 · ... · n , viene dado por

$${\displaystyle \ln(n!)=\ln(1)+\ln(2)+\cdots +\ln(n).}$$

la fórmula de Stirlingn !n^[91]

Generalizaciones

logaritmo complejo

Forma polar de z = x + iy . Tanto φ como φ' son argumentos de z .

Todos los números complejos que resuelven la ecuación.

$${\displaystyle e^{a}=z}$$

se llaman logaritmos complejos de z , cuando z es (considerado como) un número complejo. Un número complejo se representa comúnmente como z = x + iy , donde xey son números reales e i es una unidad imaginaria , cuyo cuadrado es −1. Un número así puede visualizarse mediante un punto en el plano complejo , como se muestra a la derecha. La forma polar codifica un número complejo distinto de cero  z por su valor absoluto , es decir, la distancia (positiva, real)  r al origen , y un ángulo entre el eje real ( x ) Re y la línea que pasa por el origen. y z . Este ángulo se llama argumento de z . 

El valor absoluto r de z está dado por

$${\displaystyle \textstyle r={\sqrt {x^{2}+y^{2}}}.}$$

Usando la interpretación geométrica del seno y el coseno y su periodicidad en 2 π , cualquier número complejo  z puede denotarse como

$${\displaystyle z=x+iy=r(\cos \varphi +i\sin \varphi )=r(\cos(\varphi +2k\pi )+i\sin(\varphi +2k\pi )),}$$

para cualquier número entero  k . Evidentemente el argumento de z no está especificado de forma única: tanto φ como φ' = φ + 2 k π son argumentos válidos de z para todos los enteros  k , porque sumar 2 k π  radianes o k ⋅360° ^{[nb 7]} a φ corresponde a "enrollándose" alrededor del origen en el sentido contrario a las agujas del reloj k  vueltas . El número complejo resultante es siempre z , como se ilustra a la derecha para k = 1 . Se puede seleccionar exactamente uno de los posibles argumentos de z como el llamado argumento principal , denotado Arg( z ) , con A mayúscula  , exigiendo que φ pertenezca a un giro convenientemente seleccionado, por ejemplo − π < φ ≤ π ^{[ 92]} o 0 ≤ φ < 2 π . ^[93] Estas regiones, donde el argumento de z está determinado de forma única, se denominan ramas de la función del argumento.

La rama principal (- π , π ) del logaritmo complejo, Log( z ) . El punto negro en z = 1 corresponde al valor absoluto cero y los colores más brillantes se refieren a valores absolutos mayores. El tono del color codifica el argumento de Log( z ) .

La fórmula de Euler conecta las funciones trigonométricas seno y coseno con la exponencial compleja :

$${\displaystyle e^{i\varphi }=\cos \varphi +i\sin \varphi .}$$

Usando esta fórmula, y nuevamente la periodicidad, se mantienen las siguientes identidades: ^[94]

$${\displaystyle {\begin{array}{lll}z&=&r\left(\cos \varphi +i\sin \varphi \right)\\&=&r\left(\cos(\varphi +2k\pi )+i\sin(\varphi +2k\pi )\right)\\&=&re^{i(\varphi +2k\pi )}\\&=&e^{\ln(r)}e^{i(\varphi +2k\pi )}\\&=&e^{\ln(r)+i(\varphi +2k\pi )}=e^{a_{k}},\end{array}}}$$

donde ln( r ) es el único logaritmo natural real, a _k denota los logaritmos complejos de z y k es un número entero arbitrario. Por lo tanto, los logaritmos complejos de z , que son todos aquellos valores complejos a _k para los cuales la k _-ésima  potencia de e es igual a z , son los infinitos valores

${\displaystyle a_{k}=\ln(r)+i(\varphi +2k\pi ),\quad }$para enteros arbitrarios  k .

Tomando k tal que φ + 2 k π está dentro del intervalo definido para los argumentos principales, entonces a _k se llama valor principal del logaritmo, denotado Log( z ) , nuevamente con L mayúscula  . El argumento principal de cualquier número real positivo  x es 0; por lo tanto, Log( x ) es un número real y es igual al logaritmo real (natural). Sin embargo, las fórmulas anteriores para logaritmos de productos y potencias no se generalizan al valor principal del logaritmo complejo. ^[95]

La ilustración de la derecha muestra Log( z ) , confinando los argumentos de z al intervalo (−π, π] . De esta manera, la rama correspondiente del logaritmo complejo tiene discontinuidades a lo largo del eje x real negativo  , que se puede ver en el salto en el tono allí Esta discontinuidad surge al saltar al otro límite en la misma rama, al cruzar un límite, es decir, no cambiar al valor k correspondiente de la rama continuamente vecina. Tal lugar se llama corte de rama . Eliminar las restricciones de rango en el argumento convierte las relaciones "argumento de z ", y en consecuencia el "logaritmo de z ", en funciones multivaluadas .

Inversas de otras funciones exponenciales

La exponenciación ocurre en muchas áreas de las matemáticas y su función inversa a menudo se denomina logaritmo. Por ejemplo, el logaritmo de una matriz es la función inversa (multivaluada) de la matriz exponencial . ^[96] Otro ejemplo es el logaritmo p -ádico , la función inversa del exponencial p -ádico . Ambos se definen mediante series de Taylor análogas al caso real. ^[97] En el contexto de la geometría diferencial , el mapa exponencial mapea el espacio tangente en un punto de una variedad a una vecindad de ese punto. Su inversa también se llama aplicación logarítmica (o log). ^[98]

En el contexto de grupos finitos, la exponenciación se obtiene multiplicando repetidamente un elemento del grupo  b por sí mismo. El logaritmo discreto es el número entero  n resolviendo la ecuación

$${\displaystyle b^{n}=x,}$$

xla criptografía de clave públicaintercambio de claves Diffie-Hellmancriptográficas^[99] El logaritmo de Zechcampo finito^[100]

Otras funciones inversas similares a logaritmos incluyen el logaritmo doble  ln(ln( x )) , el superlogaritmo o hiperlogaritmo 4 (una ligera variación del cual se llama logaritmo iterado en informática), la función Lambert W y el logit . Son las funciones inversas de la función exponencial doble , tetración , de f ( w ) = we ^w , ^[101] y de la función logística , respectivamente. ^[102]

Conceptos relacionados

Desde la perspectiva de la teoría de grupos , la identidad log( cd ) = log( c ) + log( d ) expresa un isomorfismo de grupo entre reales positivos bajo multiplicación y reales bajo suma. Las funciones logarítmicas son los únicos isomorfismos continuos entre estos grupos. ^[103] Mediante ese isomorfismo, la medida de Haar ( medida de Lebesgue )  dx sobre los reales corresponde a la medida de Haar  dx / x sobre los reales positivos. ^[104] Los reales no negativos no sólo tienen una multiplicación, sino que también tienen una suma, y ​​forman un semianillo , llamado semianillo de probabilidad ; De hecho, esto es un semicampo . Luego, el logaritmo lleva la multiplicación a la suma (multiplicación logarítmica) y la suma a la suma logarítmica ( LogSumExp ), dando un isomorfismo de semirings entre el semiring de probabilidad y el semiring log .

Las formas logarítmicas uniformes  df / f aparecen en análisis complejos y geometría algebraica como formas diferenciales con polos logarítmicos . ^[105]

El polilogaritmo es la función definida por

$${\displaystyle \operatorname {Li} _{s}(z)=\sum _{k=1}^{\infty }{z^{k} \over k^{s}}.}$$

logaritmo naturalLi ₁  ( z ) = −ln(1 − z )Li _s  (1)función zeta de Riemann ζ( s )^[106]

Ver también

• Portal de matemáticas
• Portal aritmético
• Portal de química
• Portal de geografía
• Portal de ingeniería

• Exponente decimal (dex)
• Funcion exponencial
• Índice de artículos sobre logaritmos.

Notas

1. Las restricciones de x y b se explican en la sección "Propiedades analíticas".
2. Prueba: tomando el logaritmo en base k de la identidad definitoria que se obtiene. La fórmula sigue resolviendo para ${\textstyle x=b^{\log _{b}x},}$ ${\displaystyle \log _{k}x=\log _{k}\left(b^{\log _{b}x}\right)=\log _{b}x\cdot \log _{k}b.}$ ${\displaystyle \log _{b}x.}$
3. z Algunos matemáticos desaprueban esta notación. En su autobiografía de 1985, Paul Halmos criticó lo que consideraba la "notación infantil In " , que, según dijo, ningún matemático había utilizado jamás. ^[15] La notación fue inventada por el matemático del siglo XIX I. Stringham . ^{[16] [17]}
4. Por ejemplo C , Java , Haskell y BASIC .
5. La misma serie es válida para el valor principal del logaritmo complejo para números complejos z que satisfacen | z − 1| < 1 .
6. La misma serie es válida para el valor principal del logaritmo complejo para números complejos z con parte real positiva.
7. Consulte radianes para conocer la conversión entre 2 π y 360 grados .

Referencias

1. Hobson, Ernest William (1914), John Napier y la invención de los logaritmos, 1614; una conferencia, Bibliotecas de la Universidad de California, Cambridge: University Press
2. Remmert, Reinhold. (1991), Teoría de funciones complejas , Nueva York: Springer-Verlag, ISBN 0387971955, OCLC  21118309
3. Kate, SK; Bhapkar, HR (2009), Conceptos básicos de matemáticas , Pune: Publicaciones técnicas, ISBN 978-81-8431-755-8, Capítulo 1
4. Todas las declaraciones de esta sección se pueden encontrar en Douglas Downing 2003, p. 275 o Kate y Bhapkar 2009, pág. 1-1, por ejemplo.
5. Bernstein, Stephen; Bernstein, Ruth (1999), Esquema de la teoría y los problemas de los elementos de la estadística de Schaum. I, Estadística descriptiva y probabilidad, serie de esquemas de Schaum, Nueva York: McGraw-Hill , ISBN 978-0-07-005023-5, pag. 21
6. Derribado, Douglas (2003). Álgebra de forma fácil. Serie educativa de Barron. Hauppauge, Nueva York: Barron's. capítulo 17, pág. 275.ISBN​ 978-0-7641-1972-9.
7. Wegener, Ingo (2005). Teoría de la complejidad: exploración de los límites de los algoritmos eficientes . Berlín, DE / Nueva York, NY: Springer-Verlag . pag. 20.ISBN​ 978-3-540-21045-0.
8. van der Lubbe, enero CA (1997). Teoría de la información. Prensa de la Universidad de Cambridge. pag. 3.ISBN​ 978-0-521-46760-5.
9. Allen, Isabel; Triantaphillidou, Sophie (2011). El Manual de Fotografía. Taylor y Francisco. pag. 228.ISBN​ 978-0-240-52037-7.
10. Goodrich, Michael T .; Tamassia, Roberto (2002). Diseño de algoritmos: fundamentos, análisis y ejemplos de Internet . John Wiley e hijos. pag. 23. Uno de los aspectos interesantes y a veces incluso sorprendentes del análisis de estructuras de datos y algoritmos es la presencia ubicua de logaritmos... Como es costumbre en la literatura informática, omitimos escribir la base b del logaritmo cuando b = 2 .
11. Parkhurst, David F. (2007). Introducción a las matemáticas aplicadas a las ciencias ambientales (edición ilustrada). Medios de ciencia y negocios de Springer. pag. 288.ISBN​ 978-0-387-34228-3.
12. "Parte 2: Matemáticas". [título no citado] . Cantidades y unidades (Informe). Organización Internacional de Normalización . 2019. ISO 80000-2 :2019 / EN ISO 80000-2 .
    Véase también ISO 80000-2  .
13. Gullberg, enero (1997). Matemáticas: Del nacimiento de los números . Nueva York, Nueva York: WW Norton & Co. ISBN 978-0-393-04002-9.
14. Perl, Yehoshua; Reingold, Edward M. (diciembre de 1977). "Comprender la complejidad de la búsqueda por interpolación". Cartas de procesamiento de información . 6 (6): 219–222, nota al pie 1. doi :10.1016/0020-0190(77)90072-2.
15. Halmos, P. (1985). Quiero ser matemático: una automatografía . Berlín, DE / Nueva York, NY: Springer-Verlag. ISBN 978-0-387-96078-4.
16. Stringham, I. (1893). Álgebra uniplanar. La prensa de Berkeley. pag.  xiii . Ser parte I de una propedéutica del análisis matemático superior.
17. Freedman, Roy S. (2006). Introducción a la Tecnología Financiera. Ámsterdam: Prensa académica. pag. 59.ISBN​ 978-0-12-370478-8.
18. Rudin, Walter (1984). "Teorema 3.29". Principios de análisis matemático (3ª ed., edición para estudiantes internacionales). Auckland, Nueva Zelanda: McGraw-Hill International. ISBN 978-0-07-085613-4.
19. Napier, John (1614), Mirifici Logarithmorum Canonis Descriptio [ La descripción del maravilloso canon de logaritmos ] (en latín), Edimburgo, Escocia: Andrew Hart
    La secuela …Constructio fue publicada póstumamente:
    Napier, John (1619), Mirifici Logarithmorum Canonis Constructio [ La construcción de la maravillosa regla de los logaritmos ] (en latín), Edimburgo: Andrew Hart
    Ian Bruce ha realizado una traducción comentada de ambos libros (2012), disponible en 17centurymaths.com.
20. Hobson, Ernest William (1914), John Napier y la invención de los logaritmos, 1614, Cambridge: The University Press
21. Folkerts, Menso; Launert, Dieter; Thom, Andreas (2016), "Método de Jost Bürgi para calcular los senos", Historia Mathematica , 43 (2): 133–147, arXiv : 1510.03180 , doi :10.1016/j.hm.2016.03.001, MR  3489006, S2CID  119326088
22. O'Connor, John J.; Robertson, Edmund F. , "Jost Bürgi (1552 - 1632)", Archivo MacTutor de Historia de las Matemáticas , Universidad de St Andrews
23. William Gardner (1742) Tablas de logaritmos
24. Pierce, RC Jr. (enero de 1977), "Una breve historia de los logaritmos", The Two-Year College Mathematics Journal , 8 (1): 22–26, doi :10.2307/3026878, JSTOR  3026878
25. Enrique Gonzales-Velasco (2011) Viaje a través de las matemáticas - Episodios creativos en su historia , §2.4 Logaritmos hiperbólicos, p. 117, Springer ISBN 978-0-387-92153-2 
26. Florian Cajori (1913) "Historia de los conceptos exponencial y logaritmo", American Mathematical Monthly 20: 5, 35, 75, 107, 148, 173, 205.
27. Stillwell, J. (2010), Las matemáticas y su historia (3.ª ed.), Springer
28. Bryant, Walter W. (1907), Una historia de la astronomía, Londres: Methuen & Co, pag. 44
29. Abramowitz, Milton ; Stegun, Irene A. , eds. (1972), Manual de funciones matemáticas con fórmulas, gráficas y tablas matemáticas (10.ª ed.), Nueva York: Dover Publications , ISBN 978-0-486-61272-0, apartado 4.7., pág. 89
30. Campbell-Kelly, Martin (2003), La historia de las tablas matemáticas: de Sumer a las hojas de cálculo , beca de Oxford en línea, Oxford University Press , ISBN 978-0-19-850841-0, sección 2
31. Spiegel, Murray R.; Moyer, RE (2006), Esquema de álgebra universitaria de Schaum , Serie de esquemas de Schaum, Nueva York: McGraw-Hill , ISBN 978-0-07-145227-4, pag. 264
32. Maor, Eli (2009), E: La historia de un número , Princeton University Press , secciones 1, 13, ISBN 978-0-691-14134-3
33. Devlin, Keith (2004), Conjuntos, funciones y lógica: una introducción a las matemáticas abstractas, Matemáticas Chapman & Hall/CRC (3.ª ed.), Boca Raton, Florida: Chapman & Hall/CRC, ISBN 978-1-58488-449-1, o ver las referencias en función
34. Lang, Serge (1997), Análisis de pregrado , Textos de pregrado en matemáticas (2.a ed.), Berlín, Nueva York: Springer-Verlag , doi :10.1007/978-1-4757-2698-5, ISBN 978-0-387-94841-6, señor  1476913, sección III.3
35. Lang 1997, sección IV.2
36. Dieudonné, Jean (1969), Fundamentos del análisis moderno , vol. 1, Prensa académica, pág. 84punto (4.3.1)
37. "Cálculo de d/dx(Log(b,x))", Wolfram Alpha , Wolfram Research , consultado el 15 de marzo de 2011
38. Kline, Morris (1998), Cálculo: un enfoque físico e intuitivo , Libros de matemáticas de Dover, Nueva York: Publicaciones de Dover , ISBN 978-0-486-40453-0, pag. 386
39. "Cálculo de Integrate(ln(x))", Wolfram Alpha , Wolfram Research , consultado el 15 de marzo de 2011
40. Abramowitz y Stegun, eds. 1972, pág. 69
41. Courant, Richard (1988), Cálculo diferencial e integral. vol. I , Wiley Classics Library, Nueva York: John Wiley & Sons , ISBN 978-0-471-60842-4, señor  1009558, sección III.6
42. Havil, Julian (2003), Gamma: Explorando la constante de Euler , Princeton University Press , ISBN 978-0-691-09983-5, secciones 11.5 y 13.8
43. Nomizu, Katsumi (1996), Artículos seleccionados sobre teoría de números y geometría algebraica, vol. 172, Providence, RI: Librería AMS, pág. 21, ISBN 978-0-8218-0445-2
44. Baker, Alan (1975), Teoría de números trascendental , Cambridge University Press , ISBN 978-0-521-20461-3, pag. 10
45. Muller, Jean-Michel (2006), Funciones elementales (2ª ed.), Boston, MA: Birkhäuser Boston, ISBN 978-0-8176-4372-0, apartados 4.2.2 (pág. 72) y 5.5.2 (pág. 95)
46. Ciervo; Cheney; Lawson; et al. (1968), Aproximaciones informáticas , Serie SIAM en Matemáticas Aplicadas, Nueva York: John Wiley, sección 6.3, págs. 105-11
47. Zhang, M.; Delgado-Frías, JG; Vassiliadis, S. (1994), "Esquema de Newton impulsado por tabla para la generación de logaritmos de alta precisión", IEE Proceedings - Computers and Digital Techniques , 141 (5): 281–92, doi :10.1049/ip-cdt:19941268, ISSN  1350- 2387, sección 1 para una descripción general
48. Meggitt, JE (abril de 1962), "Procesos de pseudodivisión y pseudomultiplicación", IBM Journal of Research and Development , 6 (2): 210–26, doi :10.1147/rd.62.0210, S2CID  19387286
49. Kahan, W. (20 de mayo de 2001), Algoritmos de pseudodivisión para logaritmos y exponenciales de coma flotante
50. Abramowitz y Stegun, eds. 1972, pág. 68
51. Sasaki, T.; Kanada, Y. (1982), "Evaluación de precisión múltiple prácticamente rápida de log(x)", Journal of Information Processing , 5 (4): 247–50 , consultado el 30 de marzo de 2011
52. Ahrendt, Timm (1999), "Cálculos rápidos de la función exponencial", Stacs 99 , Apuntes de conferencias sobre informática, vol. 1564, Berlín, Nueva York: Springer, págs. 302–12, doi :10.1007/3-540-49116-3_28, ISBN 978-3-540-65691-3
53. Hillis, Danny (15 de enero de 1989), "Richard Feynman and The Connection Machine", Physics Today , 42 (2): 78, Bibcode :1989PhT....42b..78H, doi :10.1063/1.881196
54. Maor 2009, pag. 135
55. Frey, Bruce (2006), Hacks de estadísticas, Hacks Series, Sebastopol, CA: O'Reilly , ISBN 978-0-596-10164-0, capítulo 6, artículo 64
56. Ricciardi, Luigi M. (1990), Conferencias sobre informática y matemáticas aplicadas, Manchester: Manchester University Press, ISBN 978-0-7190-2671-3, pag. 21, sección 1.3.2
57. Maling, George C. (2007), "Noise", en Rossing, Thomas D. (ed.), Manual de acústica de Springer , Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-30446-5, sección 23.0.2
58. Tashev, Ivan Jelev (2009), Captura y procesamiento de sonido: enfoques prácticos, Nueva York: John Wiley & Sons , p. 98, ISBN 978-0-470-31983-3
59. Chui, CK (1997), Wavelets: una herramienta matemática para el procesamiento de señales, monografías de SIAM sobre computación y modelado matemático, Filadelfia: Sociedad de Matemáticas Industriales y Aplicadas , ISBN 978-0-89871-384-8
60. Crauder, Bruce; Evans, Benny; Noell, Alan (2008), Funciones y cambio: un enfoque de modelado para el álgebra universitaria (4ª ed.), Boston: Cengage Learning, ISBN 978-0-547-15669-9, sección 4.4.
61. Bradt, Hale (2004), Métodos astronómicos: un enfoque físico a las observaciones astronómicas , Cambridge Planetary Science, Cambridge University Press , ISBN 978-0-521-53551-9, sección 8.3, pág. 231
62. Norby, Jens (2000). "El origen y el significado de la minúscula p en pH". Tendencias en Ciencias Bioquímicas . 25 (1): 36–37. doi :10.1016/S0968-0004(99)01517-0. PMID  10637613.
63. IUPAC (1997), AD McNaught, A. Wilkinson (ed.), Compendio de terminología química ("Libro de oro") (2ª ed.), Oxford: Blackwell Scientific Publications, doi : 10.1351/goldbook , ISBN 978-0-9678550-9-7
64. Bird, JO (2001), Libro de bolsillo de matemáticas de ingeniería de Newnes (3.ª ed.), Oxford: Newnes, ISBN 978-0-7506-4992-6, artículo 34
65. Goldstein, E. Bruce (2009), Enciclopedia de la percepción, Thousand Oaks, CA: Sage, ISBN 978-1-4129-4081-8, págs. 355–56
66. Matthews, Gerald (2000), Desempeño humano: cognición, estrés y diferencias individuales, Hove: Psychology Press, ISBN 978-0-415-04406-6, pag. 48
67. Welford, AT (1968), Fundamentos de habilidad , Londres: Methuen, ISBN 978-0-416-03000-6, OCLC  219156, pag. 61
68. Paul M. Fitts (junio de 1954), "La capacidad de información del sistema motor humano para controlar la amplitud del movimiento", Journal of Experimental Psychology , 47 (6): 381–91, doi :10.1037/h0055392, PMID  13174710, S2CID  501599, reimpreso en Paul M. Fitts (1992), "La capacidad de información del sistema motor humano para controlar la amplitud del movimiento" (PDF) , Journal of Experimental Psychology: General , 121 (3): 262–69, doi :10.1037 /0096-3445.121.3.262, PMID  1402698 , consultado el 30 de marzo de 2011
69. Banerjee, JC (1994), Diccionario enciclopédico de términos psicológicos, Nueva Delhi: MD Publications, p. 304, ISBN 978-81-85880-28-0, OCLC  33860167
70. Nadel, Lynn (2005), Enciclopedia de ciencia cognitiva , Nueva York: John Wiley & Sons , ISBN 978-0-470-01619-0, lemas Psicofísica y percepción: visión general
71. Siegler, Robert S.; Opfer, John E. (2003), "El desarrollo de la estimación numérica. Evidencia de representaciones múltiples de cantidades numéricas" (PDF) , Psychology Science , 14 (3): 237–43, CiteSeerX 10.1.1.727.3696 , doi :10.1111 /1467-9280.02438, PMID  12741747, S2CID  9583202, archivado desde el original (PDF) el 17 de mayo de 2011 , consultado el 7 de enero de 2011 
72. Dehaene, Estanislao; Izard, Véronique; Spelke, Elizabeth; Pica, Pierre (2008), "¿Log o lineal? Intuiciones distintas de la escala numérica en las culturas indígenas occidentales y amazónicas", Science , 320 (5880): 1217–20, Bibcode :2008Sci...320.1217D, CiteSeerX 10.1.1.362 .2390 , doi : 10.1126/ciencia.1156540, PMC 2610411 , PMID  18511690  
73. Breiman, Leo (1992), Probabilidad , Clásicos de las matemáticas aplicadas, Filadelfia: Sociedad de Matemáticas Industriales y Aplicadas , ISBN 978-0-89871-296-4, sección 12.9
74. Aitchison, J.; Brown, JAC (1969), La distribución lognormal , Cambridge University Press , ISBN 978-0-521-04011-2, OCLC  301100935
75. Jean Mathieu y Julian Scott (2000), Introducción al flujo turbulento, Cambridge University Press, p. 50, ISBN 978-0-521-77538-0
76. Rosa, Colin; Smith, Murray D. (2002), Estadística matemática con Mathematica , Textos de estadística de Springer, Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-95234-5, sección 11.3
77. Tabachnikov, Serge (2005), Geometría y billar , Providence, RI: American Mathematical Society , págs. 36–40, ISBN 978-0-8218-3919-5, sección 2.1
78. Durtschi, Cindy; Hillison, William; Pacini, Carl (2004), "The Effective Use of Benford's Law in Detecting Fraud in Accounting Data" (PDF) , Journal of Forensic Accounting , V : 17–34, archivado desde el original (PDF) el 29 de agosto de 2017 , recuperado 28 mayo 2018
79. Wegener, Ingo (2005), Teoría de la complejidad: explorando los límites de los algoritmos eficientes , Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-21045-0, págs. 1-2
80. Harel, David; Feldman, Yishai A. (2004), Algorítmica: el espíritu de la informática , Nueva York: Addison-Wesley , ISBN 978-0-321-11784-7, pag. 143
81. Knuth, Donald (1998), El arte de la programación informática , Reading, MA: Addison-Wesley, ISBN 978-0-201-89685-5, sección 6.2.1, págs. 409–26
82. Donald Knuth 1998, sección 5.2.4, págs. 158–68
83. Wegener, Ingo (2005), Teoría de la complejidad: explorando los límites de los algoritmos eficientes , Berlín, Nueva York: Springer-Verlag , p. 20, ISBN 978-3-540-21045-0
84. Mohr, Hans; Schopfer, Peter (1995), Fisiología vegetal , Berlín, Nueva York: Springer-Verlag, ISBN 978-3-540-58016-4, capítulo 19, pág. 298
85. Eco, Umberto (1989), La obra abierta , Harvard University Press , ISBN 978-0-674-63976-8, sección III.I
86. Sprott, Julien Clinton (2010), "Caos elegante: flujos caóticos algebraicamente simples", Caos elegante: flujos caóticos algebraicamente simples. Editado por Sprott Julien Clinton. Publicado por World Scientific Publishing Co. Pte. Limitado. Ltd , Nueva Jersey: World Scientific , Bibcode : 2010ecas.book.....S, doi : 10.1142/7183, ISBN 978-981-283-881-0, sección 1.9
87. Helmberg, Gilbert (2007), Familiarizándose con los fractales , De Gruyter Textbook, Berlín, Nueva York: Walter de Gruyter, ISBN 978-3-11-019092-2
88. Wright, David (2009), Matemáticas y música , Providence, RI: Librería AMS, ISBN 978-0-8218-4873-9, Capítulo 5
89. Bateman, PT; Diamond, Harold G. (2004), Teoría analítica de números: un curso introductorio , Nueva Jersey: World Scientific , ISBN 978-981-256-080-3, OCLC  492669517, teorema 4.1
90. PT Bateman y Diamond 2004, teorema 8.15
91. Slomson, Alan B. (1991), Introducción a la combinatoria , Londres: CRC Press , ISBN 978-0-412-35370-3, Capítulo 4
92. Ganguly, S. (2005), Elementos de análisis complejo , Kolkata: Academic Publishers, ISBN 978-81-87504-86-3, Definición 1.6.3
93. Nevanlinna, Rolf Herman ; Paatero, Veikko (2007), "Introducción al análisis complejo", Londres: Hilger , Providence, RI: AMS Bookstore, Bibcode :1974aitc.book.....W, ISBN 978-0-8218-4399-4, sección 5.9
94. Moore, Theral Orvis; Hadlock, Edwin H. (1991), Análisis complejo , Singapur: World Scientific , ISBN 978-981-02-0246-0, sección 1.2
95. Wilde, Ivan Francis (2006), Apuntes de conferencias sobre análisis complejo, Londres: Imperial College Press, ISBN 978-1-86094-642-4, teorema 6.1.
96. Higham, Nicholas (2008), Funciones de matrices. Teoría y Computación , Filadelfia, PA: SIAM , ISBN 978-0-89871-646-7, Capítulo 11.
97. Neukirch, Jürgen (1999), Algebraische Zahlentheorie , Grundlehren der mathematischen Wissenschaften , vol. 322, Berlín: Springer-Verlag , ISBN 978-3-540-65399-8, SEÑOR  1697859, Zbl  0956.11021, sección II.5.
98. Hancock, Edwin R.; Martín, Ralph R.; Sabin, Malcolm A. (2009), Matemáticas de superficies XIII: 13ª Conferencia Internacional IMA York, Reino Unido, 7 al 9 de septiembre de 2009 Actas, Springer, p. 379, ISBN 978-3-642-03595-1
99. Stinson, Douglas Robert (2006), Criptografía: teoría y práctica (3.ª ed.), Londres: CRC Press , ISBN 978-1-58488-508-5
100. Lidl, Rudolf; Niederreiter, Harald (1997), Campos finitos , Cambridge University Press, ISBN 978-0-521-39231-0
101. Corless, R.; Gonnet, G.; Liebre, D.; Jeffrey, D.; Knuth, Donald (1996), "Sobre la función Lambert W" (PDF) , Avances en Matemática Computacional , 5 : 329–59, doi :10.1007/BF02124750, ISSN  1019-7168, S2CID  29028411, archivado desde el original (PDF) el 14 de diciembre de 2010 , consultado el 13 de febrero de 2011
102. Cherkassky, Vladimir; Cherkassky, Vladimir S.; Mulier, Filip (2007), Aprender a partir de datos: conceptos, teoría y métodos , serie de Wiley sobre sistemas adaptativos y de aprendizaje para procesamiento de señales, comunicaciones y control, Nueva York: John Wiley & Sons , ISBN 978-0-471-68182-3, pag. 357
103. Bourbaki, Nicolas (1998), Topología general. Capítulos 5 a 10 , Elementos de las matemáticas, Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-64563-4, señor  1726872, sección V.4.1
104. Ambartzumian, RV (1990), Cálculo de factorización y probabilidad geométrica , Cambridge University Press , ISBN 978-0-521-34535-4, sección 1.4
105. Esnault, Hélène; Viehweg, Eckart (1992), Conferencias sobre teoremas de fuga , Seminario DMV, vol. 20, Basilea, Boston: Birkhäuser Verlag, CiteSeerX 10.1.1.178.3227 , doi :10.1007/978-3-0348-8600-0, ISBN  978-3-7643-2822-1, señor  1193913, sección 2
106. Apostol, TM (2010), "Logaritmo", en Olver, Frank WJ ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), Manual de funciones matemáticas del NIST , Cambridge University Press, ISBN 978-0-521-19225-5, señor  2723248.

enlaces externos

• Medios relacionados con el logaritmo en Wikimedia Commons
• La definición del diccionario de logaritmo en Wikcionario
• Se puede encontrar una lección sobre logaritmos en Wikiversity.
• Weisstein, Eric W. , "Logaritmo", MathWorld
• Khan Academy: Logaritmos, microconferencias online gratuitas
• "Función logarítmica", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Colin Byfleet, Vídeo educativo sobre logaritmos , consultado el 12 de octubre de 2010.
• Edward Wright, Traducción del trabajo de Napier sobre logaritmos, archivado desde el original el 3 de diciembre de 2002 , recuperado 12 de octubre 2010{{citation}}: CS1 maint: unfit URL (link)
• Glaisher, James Whitbread Lee (1911), "Logaritmo"  , en Chisholm, Hugh (ed.), Encyclopædia Britannica , vol. 16 (11.ª ed.), Cambridge University Press, págs. 868–77