Ley de Fitts

Modelo predictivo del movimiento humano

Ley de Fitts: proyecto de tamaño objetivo W y distancia al objetivo D

La ley de Fitts (a menudo citada como ley de Fitts ) es un modelo predictivo del movimiento humano utilizado principalmente en la interacción hombre-ordenador y en la ergonomía . La ley predice que el tiempo necesario para moverse rápidamente hacia un área objetivo es una función de la relación entre la distancia al objetivo y el ancho del objetivo. ^[1] La ley de Fitts se utiliza para modelar el acto de señalar , ya sea tocando físicamente un objeto con una mano o un dedo, o virtualmente, apuntando a un objeto en un monitor de ordenador utilizando un dispositivo señalador . Fue desarrollada inicialmente por Paul Fitts .

Se ha demostrado que la ley de Fitts se aplica en una variedad de condiciones; con diferentes extremidades (manos, pies, ^[2] el labio inferior, ^[3] miras montadas en la cabeza ^[4] ), manipulanda (dispositivos de entrada), ^[5] entornos físicos (incluidos los submarinos ^[6] ) y poblaciones de usuarios (jóvenes, viejos, ^[7] necesidades educativas especiales, ^[8] y participantes drogados ^[9] ).

Formulación del modelo original

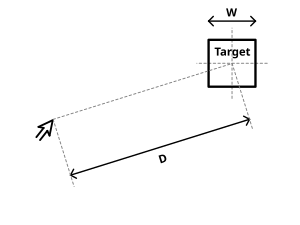
El artículo original de 1954 de Paul Morris Fitts propuso una métrica para cuantificar la dificultad de una tarea de selección de objetivos. La métrica se basaba en una analogía de información, donde la distancia al centro del objetivo ( D ) es como una señal y la tolerancia o ancho del objetivo ( W ) es como el ruido. La métrica es el índice de dificultad de Fitts ( ID , en bits):

$${\displaystyle {\text{ID}}=\log _{2}{\Bigg (}{\frac {2D}{W}}{\Bigg )}}$$

Tarea de Fitts del experimento original

Fitts también propuso un índice de rendimiento ( IP , en bits por segundo) como medida del rendimiento humano. La métrica combina el índice de dificultad de una tarea ( ID ) con el tiempo de movimiento ( MT , en segundos) en la selección del objetivo. En palabras de Fitts, "la tasa promedio de información generada por una serie de movimientos es la información promedio por movimiento dividida por el tiempo por movimiento". ^[1] Por lo tanto,

$${\displaystyle {\text{IP}}={\Bigg (}{\frac {\text{ID}}{\text{MT}}}{\Bigg )}}$$

En la actualidad, el IP se denomina más comúnmente rendimiento ( TP ). También es habitual incluir un ajuste de precisión en el cálculo.

Los investigadores posteriores a Fitts comenzaron a desarrollar ecuaciones de regresión lineal y a examinar la correlación ( r ) para determinar la bondad del ajuste. La ecuación expresa la relación entre MT y los parámetros de la tarea D y W :

$${\displaystyle {\text{MT}}=a+b\cdot {\text{ID}}=a+b\cdot \log _{2}{\Bigg (}{\frac {2D}{W}}{\Bigg )}}$$

Gráfica de la relación lineal de los parámetros de la ley de Fitts

dónde:

• MT es el tiempo promedio para completar el movimiento.
• a y b son constantes que dependen de la elección del dispositivo de entrada y suelen determinarse empíricamente mediante análisis de regresión . a define la intersección en el eje y y suele interpretarse como un retraso. El parámetro b es una pendiente y describe una aceleración. Ambos parámetros muestran la dependencia lineal en la ley de Fitts. ^[10]
• ID es el índice de dificultad.
• D es la distancia desde el punto de inicio hasta el centro del objetivo.
• W es el ancho del objetivo medido a lo largo del eje de movimiento. W también puede considerarse como la tolerancia de error permitida en la posición final, ya que el punto final del movimiento debe estar dentro de ± W ⁄ 2 del centro del objetivo.

Dado que para una tarea determinada es deseable contar con tiempos de movimiento más cortos, el valor del parámetro b se puede utilizar como métrica al comparar dispositivos señaladores de ordenador entre sí. La primera aplicación de la ley de Fitts en la interfaz hombre-ordenador fue obra de Card, English y Burr, ^[11] que utilizaron el índice de rendimiento ( IP ), interpretado como 1 ⁄ b , para comparar el rendimiento de diferentes dispositivos de entrada , siendo el ratón el mejor comparado con el joystick o las teclas de movimiento direccional. ^[11] Este trabajo temprano, según la biografía de Stuart Card , "fue un factor importante que condujo a la introducción comercial del ratón por parte de Xerox ". ^[12]

Muchos experimentos que prueban la ley de Fitts aplican el modelo a un conjunto de datos en el que se varía la distancia o el ancho, pero no ambos. El poder predictivo del modelo se deteriora cuando ambos varían en un rango significativo. ^[13] Nótese que debido a que el término ID depende solo de la relación entre la distancia y el ancho, el modelo implica que una combinación de distancia y ancho objetivo se puede reescalar arbitrariamente sin afectar el tiempo de movimiento, lo cual es imposible. A pesar de sus defectos, esta forma del modelo posee un poder predictivo notable en una variedad de modalidades de interfaz de computadora y tareas motoras, y ha proporcionado muchos conocimientos sobre los principios de diseño de interfaz de usuario.

Movimiento

Un movimiento durante una sola tarea de la ley de Fitts se puede dividir en dos fases: ^[10]

• Movimiento inicial . Un movimiento rápido pero impreciso hacia el objetivo.
• Movimiento final . Movimiento más lento pero más preciso para alcanzar el objetivo.

La primera fase se define por la distancia al objetivo. En esta fase, la distancia se puede acortar rápidamente sin perder precisión. El segundo movimiento intenta realizar un movimiento preciso, lento y controlado para alcanzar el objetivo. La duración de la tarea aumenta linealmente en relación con la dificultad. ^[10] Pero como diferentes tareas pueden tener la misma dificultad, se deduce que la distancia tiene un mayor impacto en el tiempo total de finalización de la tarea que el tamaño del objetivo.

A menudo se cita que la ley de Fitts se puede aplicar al seguimiento ocular . Este parece ser un tema al menos controvertido, como demostró Drewes. ^{[14] Durante} los movimientos sacádicos rápidos de los ojos , el usuario está ciego. Durante una tarea de la ley de Fitts, el usuario adquiere conscientemente su objetivo y puede verlo realmente, lo que hace que estos dos tipos de interacción no sean comparables.

Bits por segundo: innovaciones en modelos impulsadas por la teoría de la información

La formulación del índice de dificultad de Fitts que se utiliza con más frecuencia en la comunidad de interacción hombre-computadora se denomina formulación de Shannon:

$${\displaystyle {\text{ID}}=\log _{2}{\Bigg (}{\frac {D}{W}}+1{\Bigg )}}$$

Esta forma fue propuesta por Scott MacKenzie, ^[15] profesor de la Universidad de York , y recibió su nombre por su parecido con el teorema de Shannon-Hartley . ^[16] Describe la transmisión de información utilizando ancho de banda, intensidad de la señal y ruido. En la ley de Fitts, la distancia representa la intensidad de la señal, mientras que el ancho del objetivo es el ruido.

Utilizando esta forma del modelo, la dificultad de una tarea de señalar se equiparó a una cantidad de información transmitida (en unidades de bits) al realizar la tarea. Esto se justificó con la afirmación de que señalar se reduce a una tarea de procesamiento de información. Aunque no se estableció una conexión matemática formal entre la ley de Fitts y el teorema de Shannon-Hartley en el que se inspiró, la forma de Shannon de la ley se ha utilizado ampliamente, probablemente debido al atractivo de cuantificar las acciones motoras utilizando la teoría de la información. ^[17] En 2002 se publicó la ISO 9241 , que proporciona estándares para las pruebas de interfaz hombre-computadora, incluido el uso de la forma de Shannon de la ley de Fitts. Se ha demostrado que la información transmitida a través de pulsaciones de teclas en serie en un teclado y la información implícita en el ID para tal tarea no son consistentes. ^[18] La entropía de Shannon da como resultado un valor de información diferente al de la ley de Fitts. Los autores señalan, sin embargo, que el error es insignificante y sólo debe tenerse en cuenta en comparaciones de dispositivos con entropía conocida o en mediciones de las capacidades de procesamiento de información humana.

Ajuste de precisión: uso del ancho de objetivo efectivo

Crossman propuso una mejora importante de la ley de Fitts en 1956 (ver Welford, 1968, pp. 147-148) ^[19] y Fitts la utilizó en su artículo de 1964 con Peterson. ^[20] Con el ajuste, el ancho del objetivo ( W ) se reemplaza por un ancho de objetivo efectivo ( W _e ). W _e se calcula a partir de la desviación estándar en las coordenadas de selección recopiladas durante una secuencia de ensayos para una condición particular de DW . Si las selecciones se registran como coordenadas x a lo largo del eje de aproximación al objetivo, entonces

$${\displaystyle W_{e}=4.133\times SD_{x}}$$

Esto produce

$${\displaystyle {\text{ID}}_{e}=\log _{2}{\Bigg (}{\frac {D}{W_{e}}}+1{\Bigg )}}$$

y por lo tanto

$${\displaystyle {\text{IP}}={\Bigg (}{\frac {ID_{e}}{MT}}{\Bigg )}}$$

Si las coordenadas de selección se distribuyen normalmente, W _e abarca el 96% de la distribución. Si la tasa de error observada fue del 4% en la secuencia de ensayos, entonces W _e = W . Si la tasa de error fue mayor que el 4%, W _e > W , y si la tasa de error fue menor que el 4%, W _e < W . Al utilizar W _e , un modelo de la ley de Fitts refleja más fielmente lo que los usuarios hicieron realmente, en lugar de lo que se les pidió que hicieran.

La principal ventaja de calcular la IP como se ha indicado anteriormente es que la variabilidad espacial, o precisión, se incluye en la medición. Con el ajuste para la precisión, la ley de Fitts abarca más verdaderamente el equilibrio entre velocidad y precisión. Las ecuaciones anteriores aparecen en la norma ISO 9241-9 como el método recomendado para calcular el rendimiento .

El modelo de Welford: innovaciones impulsadas por el poder predictivo

Poco después de que se propusiera el modelo original, se propuso una variación de dos factores bajo la intuición de que la distancia y el ancho del objetivo tienen efectos separados en el tiempo de movimiento. El modelo de Welford, propuesto en 1968, separó la influencia de la distancia y el ancho del objetivo en términos separados y proporcionó un poder predictivo mejorado: ^[19]

$${\displaystyle MT=a+b_{1}\log _{2}(D)+b_{2}\log _{2}(W)}$$

Este modelo tiene un parámetro adicional, por lo que su precisión predictiva no se puede comparar directamente con las formas de un factor de la ley de Fitts. Sin embargo, una variación del modelo de Welford inspirada en la formulación de Shannon,

$${\displaystyle MT=a+b_{1}\log _{2}(D+W)+b_{2}\log _{2}(W)=a+b\log _{2}\left({\frac {D+W}{W^{k}}}\right)}$$

El parámetro adicional k permite la introducción de ángulos en el modelo. Ahora se puede tener en cuenta la posición del usuario. La influencia del ángulo se puede ponderar utilizando el exponente. Esta adición fue introducida por Kopper et al. en 2010. ^[21]

La fórmula se reduce a la forma de Shannon cuando k = 1. Por lo tanto, este modelo se puede comparar directamente con la forma de Shannon de la ley de Fitts utilizando la prueba F de modelos anidados. ^[22] Esta comparación revela que no solo la forma de Shannon del modelo de Welford predice mejor los tiempos de movimiento, sino que también es más robusta cuando se varía la ganancia de control-visualización (la relación entre, por ejemplo, el movimiento de la mano y el movimiento del cursor). En consecuencia, aunque el modelo de Shannon es ligeramente más complejo y menos intuitivo, es empíricamente el mejor modelo para usar en tareas de apuntado virtual.

Ampliación del modelo de 1D a 2D y otros matices

Extensiones a dos o más dimensiones

En su forma original, la ley de Fitts está pensada para aplicarse únicamente a tareas unidimensionales. Sin embargo, los experimentos originales requerían que los sujetos movieran un lápiz (en tres dimensiones) entre dos placas de metal sobre una mesa, lo que se denominaba tarea de golpeteo recíproco. ^[1] El ancho del objetivo perpendicular a la dirección del movimiento era muy amplio para evitar que tuviera una influencia significativa en el rendimiento. Una aplicación importante de la ley de Fitts son las tareas de apuntado virtual en 2D en pantallas de ordenador, en las que los objetivos tienen tamaños limitados en ambas dimensiones.

Tarea de toque recíproco en un contexto 2D

La ley de Fitts se ha extendido a tareas bidimensionales de dos maneras diferentes. Para navegar, por ejemplo, en menús desplegables jerárquicos, el usuario debe generar una trayectoria con el dispositivo señalador que esté limitada por la geometría del menú; para esta aplicación se derivó la ley de dirección de Accot-Zhai .

Para simplemente señalar objetivos en un espacio bidimensional, el modelo generalmente se mantiene tal como está pero requiere ajustes para capturar la geometría del objetivo y cuantificar los errores de orientación de una manera lógicamente consistente. ^{[23] [24]} Se han utilizado múltiples métodos para determinar el tamaño del objetivo: ^[25]

• status quo: ancho horizontal del objetivo
• modelo de suma: W es igual a alto + ancho
• Modelo de área: W es igual a altura * ancho
• menor del modelo: W menor valor de altura y ancho
• Modelo W: W es el ancho efectivo en la dirección del movimiento

Si bien el modelo W a veces se considera la medición de última generación, la representación verdaderamente correcta para objetivos no circulares es sustancialmente más compleja, ya que requiere calcular la convolución específica del ángulo entre la trayectoria del dispositivo apuntador y el objetivo ^[26].

Caracterización del desempeño

Dado que los parámetros a y b deben capturar los tiempos de movimiento en un rango potencialmente amplio de geometrías de tareas, pueden servir como una métrica de desempeño para una interfaz dada. Para ello, es necesario separar la variación entre usuarios de la variación entre interfaces. El parámetro a es típicamente positivo y cercano a cero, y a veces se ignora al caracterizar el desempeño promedio, como en el experimento original de Fitts. ^[18] Existen múltiples métodos para identificar parámetros a partir de datos experimentales, y la elección del método es objeto de un acalorado debate, ya que la variación del método puede resultar en diferencias de parámetros que abruman las diferencias de desempeño subyacentes. ^{[27] [28]}

Una cuestión adicional a la hora de caracterizar el rendimiento es la incorporación de la tasa de éxito: un usuario agresivo puede lograr tiempos de movimiento más cortos a costa de realizar pruebas experimentales en las que no alcance el objetivo. Si estas últimas no se incorporan al modelo, los tiempos de movimiento promedio pueden reducirse artificialmente.

Objetivos temporales

La ley de Fitts se ocupa únicamente de objetivos definidos en el espacio. Sin embargo, un objetivo puede definirse puramente en el eje del tiempo, lo que se denomina objetivo temporal. Un objetivo parpadeante o un objetivo que se mueve hacia un área de selección son ejemplos de objetivos temporales. De manera similar al espacio, la distancia al objetivo (es decir, la distancia temporal D _t ) y el ancho del objetivo (es decir, el ancho temporal W _t ) también se pueden definir para los objetivos temporales. La distancia temporal es la cantidad de tiempo que una persona debe esperar para que aparezca un objetivo. El ancho temporal es una duración corta desde el momento en que aparece el objetivo hasta que desaparece. Por ejemplo, para un objetivo parpadeante, D _t puede considerarse como el período de parpadeo y W _t como la duración del parpadeo. Al igual que con los objetivos en el espacio, cuanto mayor sea D _t o menor sea W _t , más difícil será seleccionar el objetivo.

La tarea de seleccionar el objetivo temporal se denomina apuntamiento temporal . El modelo para el apuntamiento temporal se presentó por primera vez en el campo de la interacción hombre-computadora en 2016. ^[29] El modelo predice la tasa de error, el desempeño humano en el apuntamiento temporal, como una función del índice temporal de dificultad ( ID _t ):

$${\displaystyle {\text{ID}}_{t}=\log _{2}{\Bigg (}{\frac {D_{t}}{W_{t}}}{\Bigg )}}$$

Implicaciones para el diseño de la interfaz de usuario

Rincones mágicos en Microsoft Windows

Menú radial

De las implicaciones de la ley de Fitts se pueden derivar múltiples pautas de diseño para GUI . En su forma básica, la ley de Fitts dice que los objetivos que un usuario debe alcanzar deben ser lo más grandes posible. Esto se deriva del parámetro W. Más específicamente, el tamaño efectivo del botón debe ser lo más grande posible, lo que significa que su forma debe optimizarse para la dirección del movimiento del usuario hacia el objetivo.

Los diseños también deben agrupar las funciones que se usan comúnmente entre sí. La optimización del parámetro D de esta manera permite tiempos de viaje más cortos.

La colocación de elementos de diseño en los cuatro bordes de la pantalla permite objetivos infinitamente grandes en una dimensión y, por lo tanto, presenta escenarios ideales. Dado que el puntero siempre se detendrá en el borde, el usuario puede mover el mouse con la mayor velocidad posible y aún así alcanzar el objetivo. El área del objetivo es efectivamente infinitamente larga a lo largo del eje de movimiento. Por lo tanto, esta directriz se llama "Regla de los bordes infinitos". El uso de esta regla se puede ver, por ejemplo, en MacOS , que siempre coloca la barra de menú en el borde superior izquierdo de la pantalla en lugar del marco de la ventana del programa actual. ^[30]

Este efecto se puede acentuar en las cuatro esquinas de la pantalla. En estos puntos, dos bordes chocan y forman un botón teóricamente infinitamente grande. Microsoft Windows (antes de Windows 11 ) coloca su botón de "Inicio" en la esquina inferior izquierda y Microsoft Office 2007 utiliza la esquina superior izquierda para su menú "Office". Estos cuatro puntos a veces se denominan "esquinas mágicas". ^[31] MacOS coloca el botón de cierre en el lado superior izquierdo de la ventana del programa y la barra de menú rellena la esquina mágica con otro botón.

Una interfaz de usuario que permite menús emergentes en lugar de menús desplegables fijos reduce los tiempos de desplazamiento del parámetro D. El usuario puede continuar la interacción desde la posición actual del ratón y no tiene que moverse a un área preestablecida diferente. Muchos sistemas operativos utilizan esto al mostrar menús contextuales con botón derecho. Como el menú comienza justo en el píxel en el que el usuario hizo clic, este píxel se conoce como el píxel "mágico" o "píxel principal". ^[25]

James Boritz et al. (1991) ^[32] compararon los diseños de menús radiales . En un menú radial, todos los elementos tienen la misma distancia del píxel principal. La investigación sugiere que en las implementaciones prácticas también se debe tener en cuenta la dirección en la que el usuario debe mover el mouse. Para los usuarios diestros, seleccionar el elemento del menú ubicado más a la izquierda fue significativamente más difícil que el del menú ubicado más a la derecha. No se encontraron diferencias en las transiciones de funciones superiores a inferiores y viceversa.

Véase también

• Ley de dirección de Accot-Zhai
• Ley de Hick
• Apuntar y hacer clic
• Interfaz basada en cruces

Referencias

1. Fitts, Paul M. (junio de 1954). "La capacidad de información del sistema motor humano para controlar la amplitud del movimiento". Revista de Psicología Experimental . 47 (6): 381–391. doi :10.1037/h0055392. PMID  13174710. S2CID  501599.
2. Hoffmann, Errol R. (1991). "Una comparación de los tiempos de movimiento de la mano y el pie". Ergonomía . 34 (4): 397–406. doi :10.1080/00140139108967324. PMID  1860460.
3. Jose, Marcelo Archajo; Lopes, Roleli (2015). "Interfaz hombre-computadora controlada por el labio". IEEE Journal of Biomedical and Health Informatics . 19 (1): 302–308. doi : 10.1109/JBHI.2014.2305103 . PMID  25561451.
4. Por lo tanto, RHY; Griffin, MJ (2000). "Efectos de la señal de dirección del movimiento del objetivo en el rendimiento del seguimiento de la cabeza". Ergonomía . 43 (3): 360–376. doi :10.1080/001401300184468. PMID  10755659. S2CID  40311484.
5. MacKenzie, I. Scott; Sellen, A.; Buxton, WAS (1991). "Una comparación de dispositivos de entrada en tareas de apuntar y arrastrar elementos". Actas de la Conferencia SIGCHI sobre factores humanos en sistemas informáticos - CHI '91 . págs. 161–166. doi :10.1145/108844.108868. ISBN 978-0897913836.S2CID 7637584  .
6. Kerr, R (1973). "Tiempo de movimiento en un entorno submarino". Journal of Motor Behavior . 5 (3): 175–178. doi :10.1080/00222895.1973.10734962. PMID  23961747.
7. Brogmus, G (1991). "Efectos de la edad y el sexo en la velocidad y precisión de los movimientos de la mano: y los refinamientos que sugieren para la ley de Fitts". Actas de la Reunión Anual de la Sociedad de Factores Humanos . 35 (3): 208–212. doi :10.1177/154193129103500311. S2CID  143675256.
8. Smits-Engelsman, BCM; Wilson, PH; Westenberg, Y.; Duysens, J. (2003). "Deficiencias motoras finas en niños con trastorno del desarrollo de la coordinación y discapacidades de aprendizaje: un déficit subyacente de control de circuito abierto". Human Movement Science . 22 (4–5): 495–513. doi :10.1016/j.humov.2003.09.006. PMID  14624830.
9. Kvålseth, TO (1977). "Efectos de la marihuana en el tiempo de reacción y el control motor humanos". Perceptual and Motor Skills . 45 (3): 935–939. doi :10.2466/pms.1977.45.3.935. PMID  600655. S2CID  39382776.
10. Graham, ED; MacKenzie, CL (1996). "Señalización física versus virtual". Actas de la Conferencia SIGCHI sobre factores humanos en sistemas informáticos : 292–299.
11. Card, Stuart K.; English, William K.; Burr, Betty J. (1978). "Evaluación de un ratón, un joystick isométrico controlado por velocidad, teclas de paso y teclas de texto para la selección de texto en un CRT" (PDF) . Ergonomía . 21 (8): 601–613. CiteSeerX 10.1.1.606.2223 . doi :10.1080/00140137808931762. S2CID  59725361. 
12. "Stuart Card". PARC . Archivado desde el original el 11 de julio de 2012.
13. Graham, Evan (1996). Señalar en una pantalla de ordenador (Ph.D.). Universidad Simon Fraser.
14. Drewes, H. (2011). "Disertación". Seguimiento de la mirada para la interacción persona-computadora . LMU München: Fakultät für Mathematik, Informatik und Statistik.
15. MacKenzie, I. Scott. "Página de inicio de Scott MacKenzie". www.yorku.ca .
16. MacKenzie, I. Scott (1992). "La ley de Fitts como herramienta de investigación y diseño en la interacción hombre-ordenador" (PDF) . Interacción hombre-ordenador . 7 : 91–139. doi :10.1207/s15327051hci0701_3. S2CID  14313454.
17. Drewes, Heiko (19 de abril de 2023). "La burbuja de filtros de la ley de Fitts". Resúmenes ampliados de la Conferencia CHI de 2023 sobre factores humanos en sistemas informáticos . ACM. págs. 1–5. doi :10.1145/3544549.3582739. ISBN 978-1-4503-9422-2. Número de identificación del sujeto  258217343.
18. Soukoreff, R. William; Zhao, Jian; Ren, Xiangshi (2011). "La entropía de un movimiento rápido y dirigido: índice de dificultad de Fitts frente a la entropía de Shannon". Interacción hombre-ordenador : 222–239.
19. Welford, AT (1968). Fundamentos de la habilidad . Methuen.
20. Fitts, Paul M.; Peterson, JR (1964). "Capacidad de información de respuestas motoras discretas". Revista de Psicología Experimental . 67 (2): 103–112. doi :10.1037/h0045689. PMID  14114905.
21. Kopper, R.; Bowman, DA; Silva, MG; MacMahan, RP (2010). "Un modelo de comportamiento motor humano para tareas de apuntamiento distal". Revista internacional de estudios humanos y computadores . 68 (10): 603–615. doi :10.1016/j.ijhcs.2010.05.001. S2CID  12530345.
22. Shoemaker, Garth; Tsukitani, Takayuki; Kitamura, Yoshifumi; Booth, Kellogg (diciembre de 2012). "Los modelos de dos partes capturan el impacto de la ganancia en el rendimiento de apuntado". ACM Transactions on Computer-Human Interaction . 19 (4): 1–34. doi : 10.1145/2395131.2395135 . S2CID  6201126.
23. Wobbrock, J.; Shinohara, K (2011). "Los efectos de la dimensionalidad de la tarea, la desviación del punto final, el cálculo del rendimiento y el diseño de experimentos en medidas y modelos de apuntamiento". Actas de la Conferencia SIGCHI sobre factores humanos en sistemas informáticos . Vancouver, Columbia Británica. págs. 1639–1648. CiteSeerX 10.1.1.409.2785 . doi :10.1145/1978942.1979181. ISBN .  9781450302289.S2CID18568166  .​{{cite book}}: Mantenimiento de CS1: falta la ubicación del editor ( enlace )
24. MacKenzie, I. Scott; Buxton, William AS (1992). "Extensión de la ley de Fitts a tareas bidimensionales". Actas de la conferencia SIGCHI sobre factores humanos en sistemas informáticos - CHI '92. págs. 219-226. doi :10.1145/142750.142794. ISBN 978-0897915137. Número de identificación del sujeto  358907.
25. Zhao, H. (2002). "Ley de Fitt: modelado del tiempo de movimiento en HCI". Teorías en interacción humano-computadora . S2CID  17219815.
26. Grossman, Tovi; Balakrishnan, Ravin (septiembre de 2005). "Un enfoque probabilístico para modelar el apuntamiento bidimensional". ACM Transactions on Computer-Human Interaction . 12 (3): 435–459. CiteSeerX 10.1.1.61.5707 . doi :10.1145/1096737.1096741. S2CID  8809382. {{cite journal}}: Mantenimiento CS1: fecha y año ( enlace )
27. Soukoreff, R. William; MacKenzie, I. Scott (2004). "Hacia un estándar para la evaluación de dispositivos señaladores, perspectivas sobre 27 años de investigación de la ley de Fitts en HCI" (PDF) . Revista internacional de estudios humanos-informáticos . 61 (6): 751–789. doi :10.1016/j.ijhcs.2004.09.001. S2CID  12224119.
28. Zhai, Shumin (2002). Sobre la validez del rendimiento como característica de la entrada de datos de la computadora (pdf) (informe técnico). San José, California: Almaden Research Center. RJ 10253.
29. Lee, Byungjoo; Oulasvirta, Antti (2016). "Tasas de error de modelado en el apuntamiento temporal". Actas de la Conferencia CHI de 2016 sobre factores humanos en sistemas informáticos . CHI '16. Nueva York, NY, EE. UU.: ACM. págs. 1857–1868. doi :10.1145/2858036.2858143. ISBN 9781450333627.S2CID 12949535  .
30. Hale, K (2007). "Visualización de la ley de Fitts". Particletree. Archivado desde el original el 8 de diciembre de 2019. Consultado el 8 de diciembre de 2019 .
31. Jensen, H. (2006). "Giving You Fitts". Microsoft Developer. Archivado desde el original el 8 de diciembre de 2019. Consultado el 8 de diciembre de 2019 .
32. Boritz, J; Cowan, WB (1991). "Estudios de la ley de Fitts sobre el movimiento direccional del ratón". Human Performance . 1 (6). S2CID  43676399.

Bibliografía

• Accot, Johnny; Zhai, Shumin (2002). "Más que poner los puntos sobre las íes: fundamentos para interfaces basadas en cruces". Actas de la Conferencia SIGCHI sobre factores humanos en sistemas informáticos . págs. 73–80. doi :10.1145/503376.503390. ISBN 978-1581134537.S2CID2344946  .​
• Accot, Johnny; Zhai, Shumin (2003). "Refinamiento de los modelos de la ley de Fitts para el apuntamiento bivariado". Actas de la Conferencia SIGCHI sobre factores humanos en sistemas informáticos . págs. 193–200. doi :10.1145/642611.642646. ISBN. 978-1581136302. Número de identificación del sujeto  5154061.
• Card, Stuart K.; Moran, Thomas P.; Newell, Allen (1983). La psicología de la interacción entre humanos y computadoras . Hillsdale, NJ: L. Erlbaum Associates. ISBN 978-0898592436.
• Fitts, Paul M.; Peterson, James R. (febrero de 1964). "Capacidad de información de respuestas motoras discretas". Revista de Psicología Experimental . 67 (2): 103–112. doi :10.1037/h0045689. PMID  14114905.

Enlaces externos

• Una visualización interactiva de la ley de Fitts con JavaScript y D3 por Simon Wallner
• La Ley de Fitts en el Departamento de Ciencias de la Computación. Proyecto de infraestructura educativa con apoyo de la NSF
• Ley de Fitts: modelado del tiempo de movimiento en HCI
• Bibliografía de la Ley de Fitts Investigación compilada por I. Scott MacKenzie
• Software de la Ley de Fitts: descarga gratuita de I. Scott MacKenzie
• Un cuestionario diseñado para hacerte reaccionar, por Bruce Tognazzini