Radián
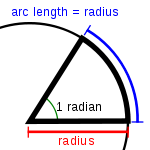
El radián mide el ángulo presentado como central a una circunferencia y su medida es igual a la razón entre la longitud del arco que comprende de dicha circunferencia y la longitud del radio, es decir, mide la cantidad de veces que la longitud del radio traza ese determinado arco en la circunferencia.
[2] Esta unidad se utiliza primordialmente en física, cálculo infinitesimal, trigonometría, goniometría, etc. Un radián es la unidad de medida de un ángulo con vértice en el centro de un círculo cuyos lados son cortados por el arco de la circunferencia, y que además dicho arco tiene una longitud igual a la del radio.
, que subtiende una circunferencia de radio r, medido en radianes, es: De forma más general, la magnitud en radianes de un ángulo subtendido es igual al cociente entre la longitud del arco y el radio del círculo; es decir,
, donde θ es el ángulo subtendido en radianes, s es la longitud del arco y r es el radio.
La relación 2π rad = 360° se puede derivar usando la fórmula para longitud de arco,
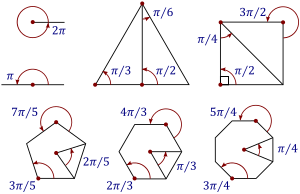
El radián es una unidad sumamente útil para medir ángulos, puesto que simplifica los cálculos, ya que los más comunes se expresan mediante sencillos múltiplos o divisores de π.
La Oficina Internacional de Pesas y Medidas[6] y la Organización Internacional de Normalización[7] especifican rad como símbolo del radián.
En la escritura matemática, a menudo se omite el símbolo "rad".
Por ejemplo, la función seno de un ángulo x expresado en radianes cumple: Análogamente los desarrollos Taylor de las funciones seno y coseno son: donde x se expresa en radianes.
El ángulo plano se define como θ = s/r, {donde θ es el ángulo subtendido en radianes, s es la longitud del arco, y r es el radio.
Un cálculo similar utilizando el área de un sector circular θ = 2A/r2 da 1 radián como 1 m2/m2.
[9] El hecho clave es que el radián es una unidad adimensional igual a 1.
[11][12] En 1993 la American Association of Physics Teachers Metric Committee especificó que el radián debía aparecer explícitamente en las cantidades sólo cuando se obtuvieran valores numéricos diferentes al utilizar otras medidas angulares, como en las cantidades de dida angular (rad), velocidad angular (rad/s), aceleración angular (rad/s2), y rigidez de torsión (N⋅m/rad), y no en las cantidades de par de torsión (N⋅m) y momento angular (kg⋅m2/s).
[13] Giacomo Prando afirma que "el estado actual de las cosas conduce inevitablemente a apariciones y desapariciones fantasmales del radián en el análisis dimensional de las ecuaciones físicas".
[14] Por ejemplo, un objeto colgado de una cuerda de una polea subirá o bajará y = rθ centímetros, donde r es el radio de la polea en centímetros y θ es el ángulo que gira la polea en radianes.
Al multiplicar r por θ la unidad de radianes desaparece del resultado.
Del mismo modo, en la fórmula para la velocidad angular de una rueda rodante, ω = v/r, los radianes aparecen en las unidades de ω pero no en el lado derecho.
[15] Anthony French llama a este fenómeno "un problema perenne en la enseñanza de la mecánica".
[16] Oberhofer dice que el consejo típico de ignorar los radianes durante el análisis dimensional y añadir o quitar radianes en las unidades según la convención y el conocimiento contextual es "pedagógicamente insatisfactorio".
La primera opción cambia la unidad de un radio a metros por radián, pero esto es incompatible con el análisis dimensional para el área del círculo, πr2.
Según Quincey, este enfoque es "lógicamente riguroso" en comparación con el SI, pero requiere "la modificación de muchas ecuaciones matemáticas y físicas familiares".
[21][22] Con este cambio, la fórmula para el ángulo subtendido en el centro de un círculo, s = rθ, se modifica para convertirse en s = ηrθ, y la serie de Taylor para el seno de un ángulo θ pasa a ser: [20][23]
si está claro que se refiere a la forma completa.
[20][25] El SI puede considerarse en relación con este marco como un sistema de unidades naturales en el que se supone que se cumple la ecuación η = 1, o de forma similar, 1 rad = 1.
Esta convención del radián permite omitir η en las fórmulas matemáticas.
[26] Una constante dimensional para el ángulo es "bastante extraña" y es probable que la dificultad de modificar las ecuaciones para añadir la constante dimensional impida su uso generalizado.
[20] Definir el radián como unidad base puede ser útil para el software, donde la desventaja de ecuaciones más largas es mínima.
La tabla muestra la conversión de los ángulos más comunes.
Análogamente, para pasar una cantidad y de rad/s a rpm tenemos que multiplicarla por 30/π:
Los grados y los radianes son dos diferentes sistemas para medir ángulos.