Momento angular

Esta magnitud desempeña respecto a las rotaciones un papel análogo al momento lineal en las traslaciones.Bajo ciertas condiciones de simetría rotacional de los sistemas es una magnitud física que se mantiene constante con el tiempo a medida que el sistema va cambiando, lo cual da lugar a la llamada ley de conservación del momento cinético.El momento cinético para un cuerpo rígido que rota respecto a un eje es la resistencia que ofrece dicho cuerpo a la variación de la velocidad angular.Sin embargo, eso no implica que sea una magnitud exclusiva de las rotaciones; por ejemplo, el momento cinético de una partícula que se mueve libremente con velocidad constante (en módulo y dirección) también se conserva.en el dibujo), definido este como la distancia del punto respecto al que se toma el momento a la recta que contiene la velocidad de la partícula.Al ser mucho más larga la llave inglesa que el radio de la tuerca, hacer un poco de fuerza en la llave obliga a la tuerca a hacer una fuerza mucho mayor para poder frenar su avance, lo cual implica que llaves más grandes permiten apretar tuercas a mayores presiones.Pero cada fuerza entre partículas tiene su reacción que es igual pero de dirección opuesta y colineal.Es decir, la suma de todos los momentos de origen interno es cero y no puede hacer cambiar el valor del momento cinético del conjunto.Donde: Ahora bien, normalmente para un sólido rígido el tensor de inerciaPor eso resulta más útil plantear las ecuaciones de movimiento en un sistema no inercial formado por los ejes principales de inercia del sólido, así se logra queQue resulta ser una ecuación no lineal en la velocidad angular.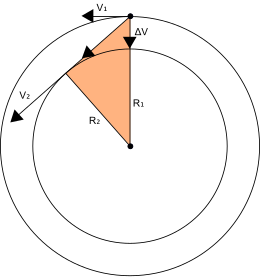Por ejemplo: En el dibujo de la derecha tenemos una masa que gira, tenida por un hilo de masa despreciable que pasa por un tubito fino.Suponemos el conjunto sin rozamientos y no tenemos en cuenta la gravedad.Si tiramos del hilo, el radio de giro disminuirá.En el dibujo siguiente aparece la masa que gira con un radioEl término correcto del "tirón" física es un impulso, es decir una fuerza aplicada durante un instante de tiempo.La dirección de esa nueva velocidad no es tangencial, sino entrante.Lo cual nos permite escribir: o sea: Y, si multiplicamos por la masa, obtenemos que el momento cinético se ha conservado, como lo esperábamos: Vemos como el momento cinético se ha conservado: Para reducir el radio de giro hay que comunicar una velocidad radial, la cual aumenta la velocidad total de la masa.Si se suelta el hilo, la masa sigue la tangente de la trayectoria y su momento cinético no cambia.Se puede hacer de manera continua, ya que la fuerza que se hace recobrando y soltando hilo puede descomponerse en una sucesión de pequeños impulsos.Una representación del momento cinético en la teoría especial de la relatividad es por tanto como cuadritensor antisimétrico:Puede verse que los 3 componentes espaciales forman el momento cinético de la mecánica newtonianadescriben el movimiento del centro de masas relativista.Y que además satisfacen las siguientes relaciones de conmutación canónicas:El momento cinético orbital, tal como el que tiene un sistema de dos partículas que gira una alrededor de la otra, se puede transformar a un operadorEn cambio en coordenadas angulares esféricas el cuadrado del momento cinético y la componente Z se expresan como:Tienen especial importancia por ser la componente angular de los orbitales atómicos.Es importante notar que si el hamiltoniano no depende de las variables angulares, como sucede por ejemplo en problemas con potencial de simetría esférica entonces todas las componentes del momento cinético conmutan con el hamiltoniano:Sin embargo, sí se pueden definir simultáneamente el cuadrado del momento cinético y una de sus componentes (habitualmente se elige la componente Z).