Función integral logarítmica

Función especial definida por una integral

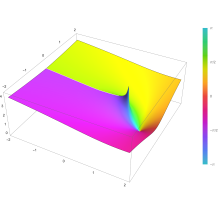
Gráfico de la función integral logarítmica li(z) en el plano complejo desde -2-2i hasta 2+2i con colores creado con la función ComplexPlot3D de Mathematica 13.1

En matemáticas , la función integral logarítmica o logaritmo integral li( x ) es una función especial . Es relevante en problemas de física y tiene importancia en la teoría de números . En particular, según el teorema de los números primos , es una muy buena aproximación a la función de conteo de primos , que se define como el número de números primos menores o iguales a un valor dado . ${\displaystyle x}$

Gráfica de función integral logarítmica

Representación integral

La integral logarítmica tiene una representación integral definida para todos los números reales positivos x  ≠ 1 por la integral definida

${\displaystyle \operatorname {li} (x)=\int _{0}^{x}{\frac {dt}{\ln t}}.}$

Aquí, ln denota el logaritmo natural . La función 1/(ln t ) tiene una singularidad en t = 1 , y la integral para x > 1 se interpreta como un valor principal de Cauchy .

${\displaystyle \operatorname {li} (x)=\lim _{\varepsilon \to 0+}\left(\int _{0}^{1-\varepsilon }{\frac {dt}{\ln t}}+\int _{1+\varepsilon }^{x}{\frac {dt}{\ln t}}\right).}$

Integral logarítmica desplazada

La integral logarítmica desfasada o integral logarítmica euleriana se define como

${\displaystyle \operatorname {Li} (x)=\int _{2}^{x}{\frac {dt}{\ln t}}=\operatorname {li} (x)-\operatorname {li} (2).}$

Como tal, la representación integral tiene la ventaja de evitar la singularidad en el dominio de la integración.

De manera equivalente,

${\displaystyle \operatorname {li} (x)=\int _{0}^{x}{\frac {dt}{\ln t}}=\operatorname {Li} (x)+\operatorname {li} (2).}$

Valores especiales

La función li( x ) tiene un único cero positivo; ocurre en x ≈ 1,45136 92348 83381 05028 39684 85892 02744 94930... OEIS : A070769 ; este número se conoce como la constante de Ramanujan-Soldner .

${\displaystyle {\text{li}}({\text{Li}}^{-1}(0))={\text{li}}(2)}$≈ 1,045163 780117 492784 844588 889194 613136 522615 578151... OEIS : A069284

Aquí es donde se encuentra la función gamma incompleta . Debe entenderse como el valor principal de Cauchy de la función. ${\displaystyle -(\Gamma \left(0,-\ln 2\right)+i\,\pi )}$ ${\displaystyle \Gamma \left(a,x\right)}$

Representación en serie

La función li( x ) está relacionada con la integral exponencial Ei( x ) a través de la ecuación

${\displaystyle {\hbox{li}}(x)={\hbox{Ei}}(\ln x),\,\!}$

que es válida para x  > 0. Esta identidad proporciona una representación en serie de li( x ) como

${\displaystyle \operatorname {li} (e^{u})={\hbox{Ei}}(u)=\gamma +\ln |u|+\sum _{n=1}^{\infty }{u^{n} \over n\cdot n!}\quad {\text{ for }}u\neq 0\;,}$

donde γ ≈ 0,57721 56649 01532 ... OEIS : A001620 es la constante de Euler-Mascheroni . Una serie de convergencia más rápida de Ramanujan ^[1] es

${\displaystyle \operatorname {li} (x)=\gamma +\ln |\ln x|+{\sqrt {x}}\sum _{n=1}^{\infty }\left({\frac {(-1)^{n-1}(\ln x)^{n}}{n!\,2^{n-1}}}\sum _{k=0}^{\lfloor (n-1)/2\rfloor }{\frac {1}{2k+1}}\right).}$

Expansión asintótica

El comportamiento asintótico para x  → ∞ es

${\displaystyle \operatorname {li} (x)=O\left({\frac {x}{\ln x}}\right).}$

donde está la notación O grande . La expansión asintótica completa es ${\displaystyle O}$

${\displaystyle \operatorname {li} (x)\sim {\frac {x}{\ln x}}\sum _{k=0}^{\infty }{\frac {k!}{(\ln x)^{k}}}}$

o

${\displaystyle {\frac {\operatorname {li} (x)}{x/\ln x}}\sim 1+{\frac {1}{\ln x}}+{\frac {2}{(\ln x)^{2}}}+{\frac {6}{(\ln x)^{3}}}+\cdots .}$

Esto da el siguiente comportamiento asintótico más preciso:

${\displaystyle \operatorname {li} (x)-{\frac {x}{\ln x}}=O\left({\frac {x}{(\ln x)^{2}}}\right).}$

Como desarrollo asintótico, esta serie no es convergente : es una aproximación razonable solo si la serie se trunca en un número finito de términos y solo se emplean valores grandes de x . Este desarrollo se deduce directamente del desarrollo asintótico para la integral exponencial .

Esto implica, por ejemplo, que podemos poner li entre paréntesis como:

${\displaystyle 1+{\frac {1}{\ln x}}<\operatorname {li} (x){\frac {\ln x}{x}}<1+{\frac {1}{\ln x}}+{\frac {3}{(\ln x)^{2}}}}$

Para todos . ${\displaystyle \ln x\geq 11}$

Importancia teórica de los números

La integral logarítmica es importante en la teoría de números , ya que aparece en las estimaciones de la cantidad de números primos menores que un valor dado. Por ejemplo, el teorema de los números primos establece que:

${\displaystyle \pi (x)\sim \operatorname {li} (x)}$

donde denota el número de primos menores o iguales a . ${\displaystyle \pi (x)}$ ${\displaystyle x}$

Suponiendo la hipótesis de Riemann , obtenemos una hipótesis aún más fuerte: ^[2]

${\displaystyle |\operatorname {li} (x)-\pi (x)|=O({\sqrt {x}}\log x)}$

De hecho, la hipótesis de Riemann es equivalente a la afirmación de que:

${\displaystyle |\operatorname {li} (x)-\pi (x)|=O(x^{1/2+a})}$Para cualquier . ${\displaystyle a>0}$

Para valores pequeños , pero la diferencia cambia de signo un número infinito de veces a medida que aumenta, y la primera vez que esto sucede es en algún lugar entre 10 ¹⁹ y 1,4×10 ³¹⁶ . ${\displaystyle x}$ ${\displaystyle \operatorname {li} (x)>\pi (x)}$ ${\displaystyle x}$

Véase también

• Gramática de Jørgen Pedersen
• Número de Skewes
• Lista de integrales de funciones logarítmicas

Referencias

1. Weisstein, Eric W. "Integral logarítmica". MathWorld .
2. Abramowitz y Stegun, pag. 230, 5.1.20

• Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [junio de 1964]. "Capítulo 5". Manual de funciones matemáticas con fórmulas, gráficos y tablas matemáticas . Serie de Matemáticas Aplicadas. Vol. 55 (Novena reimpresión con correcciones adicionales de la décima impresión original con correcciones (diciembre de 1972); primera ed.). Washington DC; Nueva York: Departamento de Comercio de los Estados Unidos, Oficina Nacional de Normas; Dover Publications. pág. 228. ISBN 978-0-486-61272-0. LCCN  64-60036. MR  0167642. LCCN  65-12253.
• Temme, NM (2010), "Integrales exponenciales, logarítmicas, seno y coseno", en Olver, Frank WJ ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), Manual del NIST de funciones matemáticas , Cambridge University Press, ISBN 978-0-521-19225-5, Sr.  2723248.