La ley de Hick , o ley de Hick-Hyman , llamada así por los psicólogos británicos y estadounidenses William Edmund Hick y Ray Hyman , describe el tiempo que tarda una persona en tomar una decisión como resultado de las opciones posibles: aumentar el número de opciones aumentará el tiempo de decisión logarítmicamente . La ley de Hick-Hyman evalúa la capacidad de información cognitiva en experimentos de reacción de elección. La cantidad de tiempo que se tarda en procesar una cierta cantidad de bits en la ley de Hick-Hyman se conoce como la "tasa de ganancia de información". La implicación en lenguaje sencillo del hallazgo es que aumentar el número de opciones no aumenta directamente el tiempo para elegir. En otras palabras, el doble de opciones no da como resultado el doble de tiempo para elegir. Además, debido a que la relación es logarítmica, el aumento en el tiempo que se tarda en elegir se vuelve cada vez menor a medida que aumenta el número de opciones.
En 1868, Franciscus Donders informó sobre la relación entre la presencia de múltiples estímulos y el tiempo de reacción ante una elección. En 1885, J. Merkel descubrió que el tiempo de respuesta es mayor cuando un estímulo pertenece a un conjunto mayor de estímulos. Los psicólogos comenzaron a ver similitudes entre este fenómeno y la teoría de la información . [ ¿ Quién? ]
Hick comenzó a experimentar con esta teoría en 1951. [1] En su primer experimento, había 10 lámparas dispuestas circularmente alrededor del sujeto. Había 10 teclas Morse para cada uno de sus dedos que correspondían a estas lámparas. Un rollo de cinta perforada activaba una lámpara aleatoria cada 5 segundos; 4 bolígrafos eléctricos registraban esta activación de la lámpara en un papel en movimiento en binario de 4 bits . Cuando el sujeto tocaba la tecla correspondiente, los 4 bolígrafos registraban la respuesta, utilizando el mismo sistema. Aunque Hicks señala que su diseño experimental que utiliza un proceso de registro binario de 4 bits era capaz de mostrar hasta 15 posiciones y "todo despejado", en su experimento requirió que el dispositivo diera un registro preciso del tiempo de reacción entre 10 opciones después de un estímulo para el experimento.
Hick realizó un segundo experimento utilizando la misma tarea, pero manteniendo el número de alternativas en 10. El participante realizó la tarea las dos primeras veces con la instrucción de realizarla con la mayor precisión posible. Para la última tarea, se le pidió al participante que realizara la tarea lo más rápido posible.
Mientras Hick afirmaba que la relación entre el tiempo de reacción y el número de opciones era logarítmica, Hyman quería entender mejor la relación entre el tiempo de reacción y el número medio de opciones. En el experimento de Hyman, tenía ocho luces diferentes dispuestas en una matriz de 6x6. [2] A cada una de estas luces diferentes se le dio un nombre, por lo que se cronometró el tiempo que tardaba el participante en decir el nombre de la luz después de que se encendió. Experimentos posteriores cambiaron el número de cada tipo diferente de luz. Hyman fue responsable de determinar una relación lineal entre el tiempo de reacción y la información transmitida.
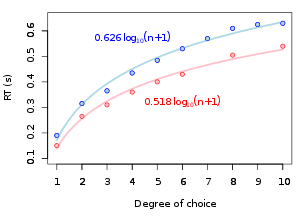
Dadas n opciones igualmente probables, el tiempo de reacción promedio T requerido para elegir entre las opciones es aproximadamente:
donde b es una constante que se puede determinar empíricamente ajustando una línea a los datos medidos. El logaritmo expresa la profundidad de la jerarquía del "árbol de elección"; log 2 indica que se realizó una búsqueda binaria . La adición de 1 a n tiene en cuenta la "incertidumbre sobre si responder o no, así como sobre qué respuesta dar". [3]
En el caso de elecciones con probabilidades desiguales, la ley se puede generalizar como:
donde H está fuertemente relacionada con la entropía teórica de la información de la decisión, definida como
donde p i se refiere a la probabilidad de que la i- ésima alternativa produzca la entropía teórica de la información.
La ley de Hick es similar en su forma a la ley de Fitts . La ley de Hick tiene una forma logarítmica porque las personas subdividen la colección total de opciones en categorías, eliminando aproximadamente la mitad de las opciones restantes en cada paso, en lugar de considerar todas y cada una de las opciones una por una, lo que requeriría un tiempo lineal.

E. Roth (1964) demostró una correlación entre el CI y la velocidad de procesamiento de la información, que es el recíproco de la pendiente de la función: [4]
donde n es el número de opciones. El tiempo que lleva tomar una decisión es:
proporcional a:
Se sabe que la compatibilidad estímulo-respuesta también afecta el tiempo de reacción ante una elección según la ley de Hick-Hyman. Esto significa que la respuesta debe ser similar al estímulo en sí (como girar el volante para hacer girar las ruedas del coche). La acción que realiza el usuario es similar a la respuesta que el conductor recibe del coche.

Estudios sugieren que la búsqueda de una palabra dentro de una lista ordenada aleatoriamente —en la que el tiempo de reacción aumenta linealmente según el número de elementos— no permite generalizar la ley científica , considerando que, en otras condiciones, el tiempo de reacción puede no estar asociado linealmente al logaritmo del número de elementos o incluso mostrar otras variaciones del plano básico.
Se han identificado excepciones a la ley de Hick en estudios de respuesta verbal a estímulos familiares, donde no hay relación o solo un aumento sutil en el tiempo de reacción asociado con un mayor número de elementos, [5] y respuestas sacádicas, donde se demostró que no hay relación, [6] o una disminución en el tiempo sacádico con el aumento del número de elementos, por lo tanto un efecto antagónico al postulado por la ley de Hick. [7]
La generalización de la ley de Hick también se puso a prueba en estudios sobre la predictibilidad de las transiciones asociadas con el tiempo de reacción de elementos que aparecieron en una secuencia estructurada. [8] [9] Este proceso se describió por primera vez como acorde con la ley de Hick, [10] pero más recientemente se demostró que la relación entre predictibilidad y tiempo de reacción es sigmoidea , no lineal, asociada con diferentes modos de acción. [11]
La ley de Hick se cita a veces para justificar las decisiones de diseño de menús . Por ejemplo, para encontrar una palabra dada (por ejemplo, el nombre de un comando) en una lista de palabras ordenadas aleatoriamente (por ejemplo, un menú), se requiere escanear cada palabra de la lista, lo que consume tiempo lineal, por lo que la ley de Hick no se aplica. Sin embargo, si la lista es alfabética y el usuario conoce el nombre del comando, puede utilizar una estrategia de subdivisión que funcione en tiempo logarítmico. [12]
{{cite book}}: CS1 maint: location missing publisher (link){{cite book}}: CS1 maint: location missing publisher (link){{cite book}}: CS1 maint: location missing publisher (link){{cite book}}: CS1 maint: location missing publisher (link)