Espacio de Hilbert

Tipo de espacio vectorial topológico

El estado de una cuerda vibrante se puede modelar como un punto en un espacio de Hilbert. La descomposición de una cuerda vibrante en sus vibraciones en distintos armónicos viene dada por la proyección del punto sobre los ejes de coordenadas en el espacio.

En matemáticas , los espacios de Hilbert (llamados así en honor a David Hilbert ) permiten generalizar los métodos de álgebra lineal y cálculo desde espacios vectoriales euclidianos (de dimensión finita) a espacios que pueden ser de dimensión infinita . Los espacios de Hilbert surgen de forma natural y frecuente en matemáticas y física , normalmente como espacios funcionales . Formalmente, un espacio de Hilbert es un espacio vectorial equipado con un producto interno que induce una función de distancia para la cual el espacio es un espacio métrico completo .

Los primeros espacios de Hilbert fueron estudiados desde este punto de vista en la primera década del siglo XX por David Hilbert , Erhard Schmidt y Frigyes Riesz . Son herramientas indispensables en las teorías de ecuaciones diferenciales parciales , mecánica cuántica , análisis de Fourier (que incluye aplicaciones al procesamiento de señales y transferencia de calor) y teoría ergódica (que constituye la base matemática de la termodinámica ). John von Neumann acuñó el término espacio de Hilbert para el concepto abstracto que subyace a muchas de estas diversas aplicaciones. El éxito de los métodos espaciales de Hilbert marcó el comienzo de una era muy fructífera para el análisis funcional . Además de los espacios vectoriales euclidianos clásicos, los ejemplos de espacios de Hilbert incluyen espacios de funciones integrables al cuadrado , espacios de secuencias , espacios de Sobolev que constan de funciones generalizadas y espacios de Hardy de funciones holomorfas .

La intuición geométrica juega un papel importante en muchos aspectos de la teoría espacial de Hilbert. Los análogos exactos del teorema de Pitágoras y la ley del paralelogramo se cumplen en un espacio de Hilbert. En un nivel más profundo, la proyección perpendicular sobre un subespacio lineal o un subespacio (el análogo de " reducir la altitud " de un triángulo ) juega un papel importante en los problemas de optimización y otros aspectos de la teoría. Un elemento de un espacio de Hilbert puede especificarse únicamente por sus coordenadas con respecto a una base ortonormal , en analogía con las coordenadas cartesianas en la geometría clásica. Cuando esta base es numerablemente infinita , permite identificar el espacio de Hilbert con el espacio de las sucesiones infinitas que son sumables al cuadrado . Este último espacio suele denominarse en la literatura más antigua espacio de Hilbert.

Definición e ilustración

Ejemplo motivador: espacio vectorial euclidiano

Uno de los ejemplos más familiares de un espacio de Hilbert es el espacio vectorial euclidiano que consta de vectores tridimensionales , denotados por R ³ y equipados con el producto escalar . El producto escalar toma dos vectores x e y y produce un número real x ⋅ y . Si xey están representados en coordenadas cartesianas , entonces el producto escalar se define por

$${\displaystyle {\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}\cdot {\begin{pmatrix}y_{1}\\y_{2}\\y_{3}\end{pmatrix}}=x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}\,.}$$

El producto escalar satisface las propiedades ^[1]

1. Es simétrico en x e y : x ⋅ y = y ⋅ x .
2. Es lineal en su primer argumento: ( a x ₁ + b x ₂ ) ⋅ y = a ( x ₁ ⋅ y ) + b ( x ₂ ⋅ y ) para cualesquiera escalares a , b y vectores x ₁ , x ₂ , y y .
3. Es definida positiva : para todos los vectores x , x ⋅ x ≥ 0 , con igualdad si y sólo si x = 0 .

Una operación sobre pares de vectores que, al igual que el producto escalar, satisface estas tres propiedades se conoce como producto interno (real) . Un espacio vectorial equipado con dicho producto interno se conoce como espacio de producto interno (real) . Todo espacio producto interior de dimensión finita es también un espacio de Hilbert. ^[2] La característica básica del producto escalar que lo conecta con la geometría euclidiana es que está relacionado tanto con la longitud (o norma ) de un vector, denotado ‖ x ‖ , como con el ángulo θ entre dos vectores x e y por medios de la fórmula

$${\displaystyle \mathbf {x} \cdot \mathbf {y} =\left\|\mathbf {x} \right\|\left\|\mathbf {y} \right\|\,\cos \theta \,.}$$

La integridad significa que si una partícula se mueve a lo largo de la trayectoria discontinua (en azul) recorriendo una distancia total finita, entonces la partícula tiene un desplazamiento neto bien definido (en naranja).

El cálculo multivariable en el espacio euclidiano se basa en la capacidad de calcular límites y de tener criterios útiles para concluir que existen límites. Una serie matemática

$${\displaystyle \sum _{n=0}^{\infty }\mathbf {x} _{n}}$$

R ³absolutamente convergente^[3]

$${\displaystyle \sum _{k=0}^{\infty }\|\mathbf {x} _{k}\|<\infty \,.}$$

Al igual que con una serie de escalares, una serie de vectores que converge absolutamente también converge a algún vector límite L en el espacio euclidiano, en el sentido de que

$${\displaystyle {\Biggl \|}\mathbf {L} -\sum _{k=0}^{N}\mathbf {x} _{k}{\Biggr \|}\to 0\quad {\text{as }}N\to \infty \,.}$$

Esta propiedad expresa la completitud del espacio euclidiano: que una serie que converge absolutamente también converge en el sentido ordinario.

Los espacios de Hilbert a menudo se ocupan de los números complejos . El plano complejo denotado por C está equipado con una noción de magnitud, el módulo complejo | z | , que se define como la raíz cuadrada del producto de z por su conjugado complejo :

$${\displaystyle |z|^{2}=z{\overline {z}}\,.}$$

Si z = x + iy es una descomposición de z en sus partes real e imaginaria, entonces el módulo es la longitud bidimensional euclidiana habitual:

$${\displaystyle |z|={\sqrt {x^{2}+y^{2}}}\,.}$$

El producto interno de un par de números complejos z y w es el producto de z con el conjugado complejo de w :

$${\displaystyle \langle z,w\rangle =z{\overline {w}}\,.}$$

Esto tiene un valor complejo. La parte real de ⟨ z , w ⟩ da el producto escalar euclidiano bidimensional habitual .

Un segundo ejemplo es el espacio C ² cuyos elementos son pares de números complejos z = ( z ₁ , z ₂ ) . Entonces el producto interno de z con otro vector similar w = ( w ₁ , w ₂ ) viene dado por

$${\displaystyle \langle z,w\rangle =z_{1}{\overline {w_{1}}}+z_{2}{\overline {w_{2}}}\,.}$$

La parte real de ⟨ z , w ⟩ es entonces el producto escalar euclidiano bidimensional. Este producto interno es simétrico hermitiano , lo que significa que el resultado de intercambiar z y w es el conjugado complejo:

$${\displaystyle \langle w,z\rangle ={\overline {\langle z,w\rangle }}\,.}$$

Definición

Un espacio de Hilbert es un espacio de producto interno real o complejo que también es un espacio métrico completo con respecto a la función de distancia inducida por el producto interno. ^[4]

Decir que un espacio vectorial complejo H es un espacio de producto interno complejo significa que existe un producto interno que asocia un número complejo a cada par de elementos de H que satisface las siguientes propiedades: ${\displaystyle \langle x,y\rangle }$ ${\displaystyle x,y}$

1. El producto interno es simétrico conjugado; es decir, el producto interno de un par de elementos es igual al conjugado complejo del producto interno de los elementos intercambiados:
   $${\displaystyle \langle y,x\rangle ={\overline {\langle x,y\rangle }}\,.}$$
   Es importante destacar que esto implica que es un número real. ${\displaystyle \langle x,x\rangle }$
2. El producto interno es lineal en su primer argumento ^{[nb 1]} . Para todos los números complejos y ${\displaystyle a}$ ${\displaystyle b,}$
   $${\displaystyle \langle ax_{1}+bx_{2},y\rangle =a\langle x_{1},y\rangle +b\langle x_{2},y\rangle \,.}$$
3. El producto interno de un elemento consigo mismo es definido positivo :
   $${\displaystyle {\begin{alignedat}{4}\langle x,x\rangle >0&\quad {\text{ if }}x\neq 0,\\\langle x,x\rangle =0&\quad {\text{ if }}x=0\,.\end{alignedat}}}$$

De las propiedades 1 y 2 se deduce que un producto interno complejo es antilineal , también llamado lineal conjugado , en su segundo argumento, lo que significa que

$${\displaystyle \langle x,ay_{1}+by_{2}\rangle ={\bar {a}}\langle x,y_{1}\rangle +{\bar {b}}\langle x,y_{2}\rangle \,.}$$

Un espacio producto interno real se define de la misma manera, excepto que H es un espacio vectorial real y el producto interno toma valores reales. Tal producto interno será un mapa bilineal y formará un sistema dual . ^[5] ${\displaystyle (H,H,\langle \cdot ,\cdot \rangle )}$

La norma es la función de valor real.

$${\displaystyle \|x\|={\sqrt {\langle x,x\rangle }}\,,}$$

H ${\displaystyle d}$ ${\displaystyle x,y}$

$${\displaystyle d(x,y)=\|x-y\|={\sqrt {\langle x-y,x-y\rangle }}\,.}$$

Que esta función sea una función de distancia significa, en primer lugar, que es simétrica en y en segundo lugar, que la distancia entre y ella misma es cero y, en caso contrario, la distancia entre y debe ser positiva y, por último, que se cumple la desigualdad del triángulo , lo que significa que la longitud de un cateto de un triángulo xyz no puede exceder la suma de las longitudes de los otros dos catetos: ${\displaystyle x}$ ${\displaystyle y,}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y}$

$${\displaystyle d(x,z)\leq d(x,y)+d(y,z)\,.}$$

Esta última propiedad es, en última instancia, una consecuencia de la desigualdad más fundamental de Cauchy-Schwarz , que afirma

$${\displaystyle \left|\langle x,y\rangle \right|\leq \|x\|\|y\|}$$

linealmente dependientes ${\displaystyle x}$ ${\displaystyle y}$

Con una función de distancia definida de esta manera, cualquier espacio producto interno es un espacio métrico y, a veces, se lo conoce como espacio de Hausdorff pre-Hilbert . ^[6] Cualquier espacio anterior a Hilbert que además sea también un espacio completo es un espacio de Hilbert. ^[7]

La completitud de H se expresa utilizando una forma del criterio de Cauchy para secuencias en H : un espacio H anterior a Hilbert es completo si cada secuencia de Cauchy converge con respecto a esta norma a un elemento en el espacio. La completitud se puede caracterizar por la siguiente condición equivalente: si una serie de vectores

$${\displaystyle \sum _{k=0}^{\infty }u_{k}}$$

converge absolutamente

$${\displaystyle \sum _{k=0}^{\infty }\|u_{k}\|<\infty \,,}$$

Hsumas parcialesH. ^[8]

Como espacio normado completo, los espacios de Hilbert son también, por definición, espacios de Banach . Como tales, son espacios vectoriales topológicos , en los que nociones topológicas como la apertura y el cierre de subconjuntos están bien definidas . De especial importancia es la noción de un subespacio lineal cerrado de un espacio de Hilbert que, con el producto interno inducido por la restricción , también es completo (siendo un conjunto cerrado en un espacio métrico completo) y por tanto un espacio de Hilbert por derecho propio.

Segundo ejemplo: espacios de secuencia

El espacio de secuencia l ² consta de todas las secuencias infinitas z = ( z ₁ , z ₂ ,…) de números complejos tales que la siguiente serie converge : ^[9]

$${\displaystyle \sum _{n=1}^{\infty }|z_{n}|^{2}}$$

El producto interior de l ² está definido por:

$${\displaystyle \langle \mathbf {z} ,\mathbf {w} \rangle =\sum _{n=1}^{\infty }z_{n}{\overline {w_{n}}}\,,}$$

Esta segunda serie converge como consecuencia de la desigualdad de Cauchy-Schwarz y la convergencia de la serie anterior.

La completitud del espacio se mantiene siempre que siempre que una serie de elementos de l ² converja absolutamente (en norma), entonces converge a un elemento de l ² . La demostración es básica en el análisis matemático y permite manipular series matemáticas de elementos del espacio con la misma facilidad que series de números complejos (o vectores en un espacio euclidiano de dimensión finita). ^[10]

Historia

David Hilbert

Antes del desarrollo de los espacios de Hilbert, los matemáticos y físicos conocían otras generalizaciones de los espacios euclidianos . En particular, la idea de un espacio lineal abstracto (espacio vectorial) había ganado cierta fuerza hacia finales del siglo XIX: ^[11] se trata de un espacio cuyos elementos se pueden sumar y multiplicar por escalares (como números reales o complejos) . ) sin identificar necesariamente estos elementos con vectores "geométricos" , como los vectores de posición y momento en los sistemas físicos. Otros objetos estudiados por los matemáticos a principios del siglo XX, en particular los espacios de secuencias (incluidas las series ) y los espacios de funciones, ^[12] pueden considerarse naturalmente como espacios lineales. Las funciones, por ejemplo, se pueden sumar o multiplicar por escalares constantes, y estas operaciones obedecen a las leyes algebraicas que se satisfacen mediante la suma y la multiplicación escalar de vectores espaciales.

En la primera década del siglo XX, desarrollos paralelos llevaron a la introducción de los espacios de Hilbert. La primera de ellas fue la observación, que surgió durante el estudio de las ecuaciones integrales de David Hilbert y Erhard Schmidt , ^[13] de que dos funciones f y g de valores reales integrables al cuadrado en un intervalo [ a , b ] tienen un producto interno

${\displaystyle \langle f,g\rangle =\int _{a}^{b}f(x)g(x)\,\mathrm {d} x}$

que tiene muchas de las propiedades familiares del producto escalar euclidiano. En particular, la idea de una familia ortogonal de funciones tiene significado. Schmidt aprovechó la similitud de este producto interno con el producto escalar habitual para demostrar un análogo de la descomposición espectral para un operador de la forma

${\displaystyle f(x)\mapsto \int _{a}^{b}K(x,y)f(y)\,\mathrm {d} y}$

donde K es una función continua simétrica en x e y . La expansión de función propia resultante expresa la función K como una serie de la forma

${\displaystyle K(x,y)=\sum _{n}\lambda _{n}\varphi _{n}(x)\varphi _{n}(y)}$

donde las funciones φ _n son ortogonales en el sentido de que ⟨ φ _n , φ _m ⟩ = 0 para todo n ≠ m . Los términos individuales de esta serie a veces se denominan soluciones de productos elementales. Sin embargo, hay expansiones de funciones propias que no logran converger en un sentido adecuado a una función integrable al cuadrado: el ingrediente faltante, que asegura la convergencia, es la integridad. ^[14]

El segundo desarrollo fue la integral de Lebesgue , una alternativa a la integral de Riemann introducida por Henri Lebesgue en 1904. ^[15] La integral de Lebesgue hizo posible integrar una clase mucho más amplia de funciones. En 1907, Frigyes Riesz y Ernst Sigismund Fischer demostraron de forma independiente que el espacio L ² de funciones cuadradas integrables de Lebesgue es un espacio métrico completo . ^[16] Como consecuencia de la interacción entre geometría y completitud, los resultados del siglo XIX de Joseph Fourier , Friedrich Bessel y Marc-Antoine Parseval sobre series trigonométricas se trasladaron fácilmente a estos espacios más generales, lo que dio como resultado un aparato geométrico y analítico que ahora suele conocido como teorema de Riesz-Fischer . ^[17]

A principios del siglo XX se demostraron más resultados básicos. Por ejemplo, el teorema de representación de Riesz fue establecido de forma independiente por Maurice Fréchet y Frigyes Riesz en 1907. ^[18] John von Neumann acuñó el término espacio abstracto de Hilbert en su trabajo sobre operadores hermitianos ilimitados . ^[19] Aunque otros matemáticos como Hermann Weyl y Norbert Wiener ya habían estudiado espacios particulares de Hilbert con gran detalle, a menudo desde un punto de vista motivado físicamente, von Neumann dio el primer tratamiento completo y axiomático de ellos. ^[20] Von Neumann los utilizó más tarde en su trabajo fundamental sobre los fundamentos de la mecánica cuántica, ^[21] y en su trabajo continuo con Eugene Wigner . El nombre "espacio de Hilbert" pronto fue adoptado por otros, por ejemplo por Hermann Weyl en su libro sobre la mecánica cuántica y la teoría de grupos. ^[22]

La importancia del concepto de espacio de Hilbert quedó subrayada al comprobar que ofrece una de las mejores formulaciones matemáticas de la mecánica cuántica . ^[23] En resumen, los estados de un sistema de mecánica cuántica son vectores en un determinado espacio de Hilbert, los observables son operadores hermitianos en ese espacio, las simetrías del sistema son operadores unitarios y las mediciones son proyecciones ortogonales . La relación entre las simetrías de la mecánica cuántica y los operadores unitarios proporcionó un impulso para el desarrollo de la teoría de la representación unitaria de grupos , iniciada en el trabajo de 1928 de Hermann Weyl. ^[22] Por otro lado, a principios de la década de 1930 quedó claro que la mecánica clásica puede describirse en términos del espacio de Hilbert ( mecánica clásica de Koopman-von Neumann ) y que ciertas propiedades de los sistemas dinámicos clásicos pueden analizarse utilizando técnicas del espacio de Hilbert en El marco de la teoría ergódica . ^[24]

El álgebra de observables en mecánica cuántica es naturalmente un álgebra de operadores definidos en un espacio de Hilbert, según la formulación de mecánica matricial de la teoría cuántica de Werner Heisenberg . ^[25] Von Neumann comenzó a investigar álgebras de operadores en la década de 1930, como anillos de operadores en un espacio de Hilbert. El tipo de álgebras estudiadas por von Neumann y sus contemporáneos se conocen ahora como álgebras de von Neumann . ^[26] En la década de 1940, Israel Gelfand , Mark Naimark e Irving Segal dieron una definición de un tipo de álgebras de operadores llamadas álgebras C* que, por un lado, no hacían referencia a un espacio de Hilbert subyacente y, por otro, extrapolaban muchos de los las características útiles de las álgebras de operadores que se habían estudiado previamente. El teorema espectral para operadores autoadjuntos en particular que subyace a gran parte de la teoría espacial de Hilbert existente se generalizó a C*-álgebras. ^[27] Estas técnicas son ahora básicas en el análisis armónico abstracto y la teoría de la representación.

Ejemplos

espacios de lebesgue

Los espacios de Lebesgue son espacios funcionales asociados a espacios de medida ( X , M , μ ) , donde X es un conjunto, M es una σ-álgebra de subconjuntos de X y μ es una medida aditiva contable en M. Sea L ² ( X , μ ) el espacio de aquellas funciones medibles de valores complejos en X para las cuales la integral de Lebesgue del cuadrado del valor absoluto de la función es finita, es decir, para una función f en L ² ( X , µ ) ,

$${\displaystyle \int _{X}|f|^{2}\mathrm {d} \mu <\infty \,,}$$

conjunto de medida cero

El producto interno de las funciones f y g en L ² ( X , μ ) se define entonces como

$${\displaystyle \langle f,g\rangle =\int _{X}f(t){\overline {g(t)}}\,\mathrm {d} \mu (t)}$$

$${\displaystyle \langle f,g\rangle =\int _{X}{\overline {f(t)}}g(t)\,\mathrm {d} \mu (t)\,,}$$

donde la segunda forma (conjugación del primer elemento) se encuentra comúnmente en la literatura de física teórica . Para f y g en L ² , la integral existe debido a la desigualdad de Cauchy-Schwarz y define un producto interno en el espacio. Equipado con este producto interior, el L ² está realmente completo. ^[28] La integral de Lebesgue es esencial para garantizar la integridad: en dominios de números reales, por ejemplo, no hay suficientes funciones que sean integrables con Riemann . ^[29]

Los espacios de Lebesgue aparecen en muchos entornos naturales. Los espacios L ² ( R ) y L ² ([0,1]) de funciones integrables al cuadrado con respecto a la medida de Lebesgue en la recta real y el intervalo unitario, respectivamente, son dominios naturales en los que definir la transformada de Fourier y la transformada de Fourier. serie. En otras situaciones, la medida puede ser algo distinto de la medida ordinaria de Lebesgue en la línea real. Por ejemplo, si w es cualquier función medible positiva, el espacio de todas las funciones medibles f en el intervalo [0, 1] que satisface

$${\displaystyle \int _{0}^{1}{\bigl |}f(t){\bigr |}^{2}w(t)\,\mathrm {d} t<\infty }$$

espacio L 2 ponderado L²
_semanas([0, 1])w

$${\displaystyle \langle f,g\rangle =\int _{0}^{1}f(t){\overline {g(t)}}w(t)\,\mathrm {d} t\,.}$$

El espacio ponderado L²
_semanas([0, 1]) es idéntico al espacio de Hilbert L ² ([0, 1], μ ) donde la medida μ de un conjunto A medible por Lebesgue está definida por

$${\displaystyle \mu (A)=\int _{A}w(t)\,\mathrm {d} t\,.}$$

Los espacios L ² ponderados como este se utilizan con frecuencia para estudiar polinomios ortogonales , porque diferentes familias de polinomios ortogonales son ortogonales con respecto a diferentes funciones de ponderación. ^[30]

espacios de sobolev

^{Los espacios de} Sobolev , denotados por Hs o Ws ^{, 2 , son espacios de} Hilbert. Se trata de un tipo especial de espacio funcional en el que se puede realizar la diferenciación , pero que (a diferencia de otros espacios de Banach como los espacios de Hölder ) sustentan la estructura de un producto interno. Como se permite la diferenciación, los espacios de Sobolev son un escenario conveniente para la teoría de ecuaciones diferenciales parciales . ^[31] También forman la base de la teoría de los métodos directos en el cálculo de variaciones . ^[32]

Para s un entero no negativo y Ω ⊂ R ⁿ , el espacio de Sobolev H ^s (Ω) contiene funciones L ² cuyas derivadas débiles de orden hasta s también son L ² . El producto interno en H ^s (Ω) es

$${\displaystyle \langle f,g\rangle =\int _{\Omega }f(x){\bar {g}}(x)\,\mathrm {d} x+\int _{\Omega }Df(x)\cdot D{\bar {g}}(x)\,\mathrm {d} x+\cdots +\int _{\Omega }D^{s}f(x)\cdot D^{s}{\bar {g}}(x)\,\mathrm {d} x}$$

s

Los espacios de Sobolev también se estudian desde el punto de vista de la teoría espectral, apoyándose más específicamente en la estructura espacial de Hilbert. Si Ω es un dominio adecuado, entonces se puede definir el espacio de Sobolev H ^s (Ω) como el espacio de potenciales de Bessel ; ^[33] aproximadamente,

$${\displaystyle H^{s}(\Omega )=\left\{(1-\Delta )^{-s/2}f\mathrel {\Big |} f\in L^{2}(\Omega )\right\}\,.}$$

Aquí Δ es el laplaciano y (1 − Δ) ^{− s  /2} se entiende en términos del teorema de mapeo espectral . Además de proporcionar una definición viable de espacios de Sobolev para números no enteros , esta definición también tiene propiedades particularmente deseables bajo la transformada de Fourier que la hacen ideal para el estudio de operadores pseudodiferenciales . Usando estos métodos en una variedad riemanniana compacta , se puede obtener, por ejemplo, la descomposición de Hodge , que es la base de la teoría de Hodge . ^[34]

Espacios de funciones holomorfas.

Espacios resistentes

Los espacios de Hardy son espacios funcionales, que surgen en el análisis complejo y el análisis armónico , cuyos elementos son ciertas funciones holomorfas en un dominio complejo. ^[35] Sea U el disco unitario en el plano complejo. Entonces el espacio de Hardy H ² ( U ) se define como el espacio de funciones holomorfas f en U tales que las medias

$${\displaystyle M_{r}(f)={\frac {1}{2\pi }}\int _{0}^{2\pi }\left|f{\bigl (}re^{i\theta }{\bigr )}\right|^{2}\,\mathrm {d} \theta }$$

permanecer acotado para r < 1 . La norma en este espacio de Hardy está definida por

$${\displaystyle \left\|f\right\|_{2}=\lim _{r\to 1}{\sqrt {M_{r}(f)}}\,.}$$

Los espacios de Hardy en el disco están relacionados con las series de Fourier. Una función f está en H ² ( U ) si y sólo si

$${\displaystyle f(z)=\sum _{n=0}^{\infty }a_{n}z^{n}}$$

$${\displaystyle \sum _{n=0}^{\infty }|a_{n}|^{2}<\infty \,.}$$

Así, H ² ( U ) consta de aquellas funciones que son L ² en el círculo y cuyos coeficientes de Fourier de frecuencia negativa desaparecen.

espacios de bergman

Los espacios de Bergman son otra familia de espacios de Hilbert de funciones holomorfas. ^[36] Sea D un conjunto abierto acotado en el plano complejo (o un espacio complejo de dimensiones superiores) y sea L ^{2, h} ( D ) el espacio de funciones holomorfas f en D que también están en L ² ( D ) en el sentido de que

$${\displaystyle \|f\|^{2}=\int _{D}|f(z)|^{2}\,\mathrm {d} \mu (z)<\infty \,,}$$

donde la integral se toma con respecto a la medida de Lebesgue en D. Claramente L ^{2, h} ( D ) es un subespacio de L ² ( D ) ; de hecho, es un subespacio cerrado y, por tanto, un espacio de Hilbert por derecho propio. Esto es una consecuencia de la estimación, válida en subconjuntos compactos K de D , que

$${\displaystyle \sup _{z\in K}\left|f(z)\right|\leq C_{K}\left\|f\right\|_{2}\,,}$$

la fórmula integral de CauchyL ² ( D )convergencia compactafDL ^{2, h} ( D )L ^{2, h} ( D )z ∈ Dη _z ∈ L ^{2, h} ( D )

$${\displaystyle f(z)=\int _{D}f(\zeta ){\overline {\eta _{z}(\zeta )}}\,\mathrm {d} \mu (\zeta )}$$

f ∈ L ^{2, h} ( D )

$${\displaystyle K(\zeta ,z)={\overline {\eta _{z}(\zeta )}}}$$

BergmanD. núcleo integral

$${\displaystyle f(z)=\int _{D}f(\zeta )K(\zeta ,z)\,\mathrm {d} \mu (\zeta )\,.}$$

Un espacio de Bergman es un ejemplo de un espacio de Hilbert con núcleo de reproducción , que es un espacio de funciones de Hilbert junto con un núcleo K ( ζ , z ) que verifica una propiedad de reproducción análoga a esta. El espacio Hardy H ² ( D ) también admite un núcleo reproductor, conocido como núcleo de Szegő . ^[37] La ​​reproducción de núcleos también es común en otras áreas de las matemáticas. Por ejemplo, en el análisis armónico , el núcleo de Poisson es un núcleo reproductor para el espacio de Hilbert de funciones armónicas integrables al cuadrado en la bola unitaria . Que este último sea un espacio de Hilbert es una consecuencia del teorema del valor medio para funciones armónicas.

Aplicaciones

Muchas de las aplicaciones de los espacios de Hilbert explotan el hecho de que los espacios de Hilbert admiten generalizaciones de conceptos geométricos simples como proyección y cambio de base desde su configuración habitual de dimensión finita. En particular, la teoría espectral de operadores lineales autoadjuntos continuos en un espacio de Hilbert generaliza la descomposición espectral habitual de una matriz , y esto a menudo juega un papel importante en las aplicaciones de la teoría a otras áreas de las matemáticas y la física.

Teoría de Sturm-Liouville

Los armónicos de una cuerda vibrante. Éstas son funciones propias de un problema asociado de Sturm-Liouville. Los valores propios 1,1/2,1/3, ... forman la serie armónica (musical) .

En la teoría de ecuaciones diferenciales ordinarias , se utilizan métodos espectrales en un espacio de Hilbert adecuado para estudiar el comportamiento de los valores propios y funciones propias de las ecuaciones diferenciales. Por ejemplo, el problema de Sturm-Liouville surge en el estudio de los armónicos de las ondas en una cuerda de violín o un tambor, y es un problema central en las ecuaciones diferenciales ordinarias . ^[38] El problema es una ecuación diferencial de la forma

$${\displaystyle -{\frac {\mathrm {d} }{\mathrm {d} x}}\left[p(x){\frac {\mathrm {d} y}{\mathrm {d} x}}\right]+q(x)y=\lambda w(x)y}$$

y[ a , b ]las condiciones generales homogéneas de frontera de Robin

$${\displaystyle {\begin{cases}\alpha y(a)+\alpha 'y'(a)&=0\\\beta y(b)+\beta 'y'(b)&=0\,.\end{cases}}}$$

pqwyλλoperadores compactosoperador integralfunción de Greenλ^{[39] [nota 2]}

Ecuaciones diferenciales parciales

Los espacios de Hilbert forman una herramienta básica en el estudio de ecuaciones diferenciales parciales . ^[31] Para muchas clases de ecuaciones diferenciales parciales, como las ecuaciones elípticas lineales , es posible considerar una solución generalizada (conocida como solución débil ) ampliando la clase de funciones. Muchas formulaciones débiles involucran la clase de funciones de Sobolev , que es un espacio de Hilbert. Una formulación débil adecuada se reduce a un problema geométrico, el problema analítico de encontrar una solución o, a menudo, lo que es más importante, mostrar que existe una solución y que es única para datos de límites dados. Para ecuaciones elípticas lineales, un resultado geométrico que garantiza una solución única para una gran clase de problemas es el teorema de Lax-Milgram . Esta estrategia forma el rudimento del método de Galerkin (un método de elementos finitos ) para la solución numérica de ecuaciones diferenciales parciales. ^[40]

Un ejemplo típico es la ecuación de Poisson −Δ u = g con condiciones de frontera de Dirichlet en un dominio acotado Ω en R ² . La formulación débil consiste en encontrar una función u tal que, para todas las funciones continuamente diferenciables v en Ω que desaparecen en la frontera:

$${\displaystyle \int _{\Omega }\nabla u\cdot \nabla v=\int _{\Omega }gv\,.}$$

Esto se puede reformular en términos del espacio de Hilbert H.¹
₀(Ω) que consta de funciones u tales que u , junto con sus derivadas parciales débiles, son integrables al cuadrado en Ω y desaparecen en la frontera. La pregunta entonces se reduce a encontrar u en este espacio tal que para todo v en este espacio

$${\displaystyle a(u,v)=b(v)}$$

donde a es una forma bilineal continua y b es un funcional lineal continuo , dado respectivamente por

$${\displaystyle a(u,v)=\int _{\Omega }\nabla u\cdot \nabla v,\quad b(v)=\int _{\Omega }gv\,.}$$

Dado que la ecuación de Poisson es elíptica , de la desigualdad de Poincaré se deduce que la forma bilineal a es coercitiva . El teorema de Lax-Milgram asegura la existencia y unicidad de las soluciones de esta ecuación. ^[41]

Los espacios de Hilbert permiten formular muchas ecuaciones diferenciales parciales elípticas de manera similar, y el teorema de Lax-Milgram es entonces una herramienta básica en su análisis. Con modificaciones adecuadas, se pueden aplicar técnicas similares a ecuaciones diferenciales parciales parabólicas y ciertas ecuaciones diferenciales parciales hiperbólicas . ^[42]

Teoría ergódica

La trayectoria de una bola de billar en el estadio Bunimovich se describe mediante un sistema dinámico ergódico .

El campo de la teoría ergódica es el estudio del comportamiento a largo plazo de los sistemas dinámicos caóticos . El caso protípico de un campo al que se aplica la teoría ergódica es la termodinámica , en la que, aunque el estado microscópico de un sistema es extremadamente complicado (es imposible comprender el conjunto de colisiones individuales entre partículas de materia), el comportamiento promedio durante un tiempo suficientemente largo intervalos de tiempo es manejable. Las leyes de la termodinámica son afirmaciones sobre ese comportamiento promedio. En particular, una formulación de la ley cero de la termodinámica afirma que en escalas de tiempo suficientemente largas, la única medición funcionalmente independiente que se puede hacer de un sistema termodinámico en equilibrio es su energía total, en forma de temperatura . ^[43]

Un sistema dinámico ergódico es aquel para el cual, aparte de la energía, medida por el hamiltoniano , no existen otras cantidades conservadas funcionalmente independientes en el espacio de fases . Más explícitamente, supongamos que la energía E es fija, y sea Ω _E el subconjunto del espacio de fases que consta de todos los estados de energía E (una superficie de energía), y sea T _t el operador de evolución en el espacio de fases. El sistema dinámico es ergódico si todas las funciones medibles invariantes en Ω _E son constantes en casi todas partes . ^[44] Una función invariante f es aquella para la cual

$${\displaystyle f(T_{t}w)=f(w)}$$

wΩ _EtEl teorema de Liouvillemedida μtraslación del tiempotransformación unitariaL ² (Ω _E , μ )Ω _E

$${\displaystyle \left\langle f,g\right\rangle _{L^{2}\left(\Omega _{E},\mu \right)}=\int _{E}f{\bar {g}}\,\mathrm {d} \mu \,.}$$

El teorema ergódico medio de von Neumann ^[24] establece lo siguiente:

• Si U _t es un semigrupo de operadores unitarios de un parámetro (fuertemente continuo) en un espacio de Hilbert H , y P es la proyección ortogonal sobre el espacio de puntos fijos comunes de U _t , { x ∈ H | U _t x = x , ∀ t > 0} , entonces
  $${\displaystyle Px=\lim _{T\to \infty }{\frac {1}{T}}\int _{0}^{T}U_{t}x\,\mathrm {d} t\,.}$$

Para un sistema ergódico, el conjunto fijo de la evolución temporal consta sólo de funciones constantes, por lo que el teorema ergódico implica lo siguiente: ^[45] para cualquier función f ∈ L ² (Ω _E , μ ) ,

$${\displaystyle {\underset {T\to \infty }{L^{2}-\lim }}{\frac {1}{T}}\int _{0}^{T}f(T_{t}w)\,\mathrm {d} t=\int _{\Omega _{E}}f(y)\,\mathrm {d} \mu (y)\,.}$$

Es decir, el promedio a largo plazo de una f observable es igual a su valor esperado sobre una superficie de energía.

análisis de Fourier

Superposición de funciones de base de onda sinusoidal (abajo) para formar una onda en diente de sierra (arriba)

Armónicos esféricos , una base ortonormal para el espacio de Hilbert de funciones integrables al cuadrado en la esfera, mostrados gráficamente a lo largo de la dirección radial

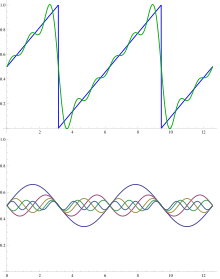
Uno de los objetivos básicos del análisis de Fourier es descomponer una función en una combinación lineal (posiblemente infinita) de funciones base dadas: la serie de Fourier asociada . La serie clásica de Fourier asociada a una función f definida en el intervalo [0, 1] es una serie de la forma

$${\displaystyle \sum _{n=-\infty }^{\infty }a_{n}e^{2\pi in\theta }}$$

$${\displaystyle a_{n}=\int _{0}^{1}f(\theta )\;\!e^{-2\pi in\theta }\,\mathrm {d} \theta \,.}$$

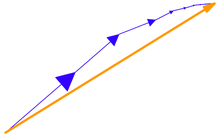
En la figura se muestra el ejemplo de sumar los primeros términos de una serie de Fourier para una función en diente de sierra. Las funciones básicas son ondas sinusoidales con longitudes de onda.λ/norte(para el número entero n ) más corto que la longitud de onda λ del propio diente de sierra (excepto para n = 1 , la onda fundamental ). Todas las funciones básicas tienen nodos en los nodos del diente de sierra, pero todas, excepto las fundamentales, tienen nodos adicionales. La oscilación de los términos sumados alrededor del diente de sierra se denomina fenómeno de Gibbs .

Un problema importante en las series de Fourier clásicas es en qué sentido la serie de Fourier converge, si es que converge, a la función f . Los métodos del espacio de Hilbert proporcionan una posible respuesta a esta pregunta. ^[46] Las funciones e _n ( θ ) = e ^{2π inθ} forman una base ortogonal del espacio de Hilbert L ² ([0, 1]) . En consecuencia, cualquier función integrable al cuadrado se puede expresar como una serie

$${\displaystyle f(\theta )=\sum _{n}a_{n}e_{n}(\theta )\,,\quad a_{n}=\langle f,e_{n}\rangle }$$

y, además, esta serie converge en el sentido del espacio de Hilbert (es decir, en la media L 2 ).

El problema también puede estudiarse desde el punto de vista abstracto: cada espacio de Hilbert tiene una base ortonormal , y cada elemento del espacio de Hilbert puede escribirse de forma única como una suma de múltiplos de estos elementos de base. Los coeficientes que aparecen sobre estos elementos básicos a veces se conocen de manera abstracta como coeficientes de Fourier del elemento del espacio. ^[47] La ​​abstracción es especialmente útil cuando es más natural utilizar diferentes funciones de base para un espacio como L ² ([0, 1]) . En muchas circunstancias, es deseable no descomponer una función en funciones trigonométricas, sino en polinomios ortogonales o wavelets , por ejemplo, ^[48] y en dimensiones superiores en armónicos esféricos . ^[49]

Por ejemplo, si e _n son funciones de base ortonormal de L ² [0, 1] , entonces una función dada en L ² [0, 1] puede aproximarse como una combinación lineal finita ^[50]

$${\displaystyle f(x)\approx f_{n}(x)=a_{1}e_{1}(x)+a_{2}e_{2}(x)+\cdots +a_{n}e_{n}(x)\,.}$$

Los coeficientes { a _j } se seleccionan para que la magnitud de la diferencia ‖ f − f _n ‖ ² sea lo más pequeña posible. Geométricamente, la mejor aproximación es la proyección ortogonal de f sobre el subespacio que consta de todas las combinaciones lineales de { e _j } , y puede calcularse mediante ^[51]

$${\displaystyle a_{j}=\int _{0}^{1}{\overline {e_{j}(x)}}f(x)\,\mathrm {d} x\,.}$$

Que esta fórmula minimice la diferencia ‖ f − f _n ‖ ² es consecuencia de la desigualdad de Bessel y la fórmula de Parseval.

En diversas aplicaciones a problemas físicos, una función se puede descomponer en funciones propias físicamente significativas de un operador diferencial (típicamente el operador de Laplace ): esto forma la base para el estudio espectral de funciones, en referencia al espectro del operador diferencial. ^[52] Una aplicación física concreta implica el problema de escuchar la forma de un tambor : dados los modos fundamentales de vibración que un parche es capaz de producir, ¿se puede inferir la forma del tambor en sí? ^[53] La formulación matemática de esta pregunta involucra los valores propios de Dirichlet de la ecuación de Laplace en el plano, que representan los modos fundamentales de vibración en analogía directa con los números enteros que representan los modos fundamentales de vibración de la cuerda del violín.

La teoría espectral también subyace a ciertos aspectos de la transformada de Fourier de una función. Mientras que el análisis de Fourier descompone una función definida en un conjunto compacto en el espectro discreto del laplaciano (que corresponde a las vibraciones de una cuerda de violín o un tambor), la transformada de Fourier de una función es la descomposición de una función definida en todo el espacio euclidiano. en sus componentes en el espectro continuo del Laplaciano. La transformación de Fourier es también geométrica, en un sentido precisado por el teorema de Plancherel , que afirma que es una isometría de un espacio de Hilbert (el "dominio del tiempo") con otro (el "dominio de la frecuencia"). Esta propiedad de isometría de la transformada de Fourier es un tema recurrente en el análisis armónico abstracto (ya que refleja la conservación de la energía para la transformada de Fourier continua), como lo demuestra, por ejemplo, el teorema de Plancherel para funciones esféricas que ocurren en el análisis armónico no conmutativo .

Mecánica cuántica

Los orbitales de un electrón en un átomo de hidrógeno son funciones propias de la energía .

En la formulación matemáticamente rigurosa de la mecánica cuántica , desarrollada por John von Neumann , ^[54] los estados posibles (más precisamente, los estados puros ) de un sistema mecánico cuántico están representados por vectores unitarios (llamados vectores de estado ) que residen en un complejo separable de Hilbert. espacio, conocido como espacio de estados , bien definido hasta un número complejo de norma 1 (el factor de fase ). En otras palabras, los estados posibles son puntos en la proyectivización de un espacio de Hilbert, habitualmente llamado espacio proyectivo complejo . La naturaleza exacta de este espacio de Hilbert depende del sistema; por ejemplo, los estados de posición y momento para una sola partícula de espín cero no relativista es el espacio de todas las funciones integrables al cuadrado , mientras que los estados para el espín de un solo protón son elementos unitarios del complejo bidimensional Espacio de espinores de Hilbert . Cada observable está representado por un operador lineal autoadjunto que actúa sobre el espacio de estados. Cada estado propio de un observable corresponde a un vector propio del operador, y el valor propio asociado corresponde al valor del observable en ese estado propio. ^[55]

El producto interno entre dos vectores de estado es un número complejo conocido como amplitud de probabilidad . Durante una medición ideal de un sistema de mecánica cuántica, la probabilidad de que un sistema colapse desde un estado inicial dado a un estado propio particular está dada por el cuadrado del valor absoluto de las amplitudes de probabilidad entre los estados inicial y final. ^[56] Los posibles resultados de una medición son los valores propios del operador, lo que explica la elección de operadores autoadjuntos, ya que todos los valores propios deben ser reales. La distribución de probabilidad de un observable en un estado determinado se puede encontrar calculando la descomposición espectral del operador correspondiente. ^[57]

Para un sistema general, los estados normalmente no son puros, sino que se representan como mezclas estadísticas de estados puros, o estados mixtos, dados por matrices de densidad : operadores autoadjuntos de traza uno en un espacio de Hilbert. ^[58] Además, para los sistemas de mecánica cuántica generales, los efectos de una sola medición pueden influir en otras partes de un sistema de una manera que se describe mediante una medida positiva valorada por el operador . Así, la estructura tanto de los estados como de los observables en la teoría general es considerablemente más complicada que la idealización de los estados puros. ^[59]

Teoría de probabilidad

En teoría de la probabilidad , los espacios de Hilbert también tienen diversas aplicaciones. Aquí, un espacio de Hilbert fundamental es el espacio de variables aleatorias en un espacio de probabilidad dado , que tiene clase (primer y segundo momento finitos ). Una operación común en estadística es la de centrar una variable aleatoria restándole su expectativa . Por tanto, si es una variable aleatoria, entonces es su centrado. En la vista del espacio de Hilbert, esta es la proyección ortogonal de sobre el núcleo del operador de expectativa, que es un funcional lineal continuo en el espacio de Hilbert (de hecho, el producto interno con la variable aleatoria constante 1), por lo que este núcleo es un subespacio cerrado. ${\displaystyle L^{2}}$ ${\displaystyle X}$ ${\displaystyle X-E(X)}$ ${\displaystyle X}$

La expectativa condicional tiene una interpretación natural en el espacio de Hilbert. ^[60] Supongamos que se da un espacio de probabilidad , donde es un álgebra sigma en el conjunto y es una medida de probabilidad en el espacio de medidas . Si es una subálgebra sigma de , entonces la expectativa condicional es la proyección ortogonal de sobre el subespacio de que consta de funciones medibles. Si la variable aleatoria in es independiente del álgebra sigma, entonces la expectativa condicional , es decir, su proyección sobre las funciones medibles es constante. De manera equivalente, la proyección de su centrado es cero. ${\displaystyle (\Omega ,P,{\mathcal {B}})}$ ${\displaystyle {\mathcal {B}}}$ ${\displaystyle \Omega }$ ${\displaystyle P}$ ${\displaystyle (\Omega ,{\mathcal {B}})}$ ${\displaystyle {\mathcal {F}}\leq {\mathcal {B}}}$ ${\displaystyle {\mathcal {B}}}$ ${\displaystyle E[X|{\mathcal {F}}]}$ ${\displaystyle X}$ ${\displaystyle L^{2}(\Omega ,P)}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle X}$ ${\displaystyle L^{2}(\Omega ,P)}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle E(X|{\mathcal {F}})=E(X)}$ ${\displaystyle {\mathcal {F}}}$

En particular, si dos variables aleatorias y (en ) son independientes, entonces las variables aleatorias centradas y son ortogonales. (Esto significa que las dos variables tienen covarianza cero : no están correlacionadas ). En ese caso, el teorema de Pitágoras en el núcleo del operador de expectativa implica que las varianzas de y satisfacen la identidad: ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle L^{2}(\Omega ,P)}$ ${\displaystyle X-E(X)}$ ${\displaystyle Y-E(Y)}$ ${\displaystyle X}$ ${\displaystyle Y}$

$${\displaystyle \operatorname {Var} (X+Y)=\operatorname {Var} (X)+\operatorname {Var} (Y),}$$

la regresión lineal^[61]análisis de varianza

La teoría de las martingalas se puede formular en espacios de Hilbert. Una martingala en un espacio de Hilbert es una secuencia de elementos de un espacio de Hilbert tal que, para cada n , es la proyección ortogonal de sobre el casco lineal de . ^[62] Si son variables aleatorias, esto reproduce la definición habitual de martingala (discreta): la expectativa de , condicionada a , es igual a . ${\displaystyle x_{1},x_{2},\dots }$ ${\displaystyle x_{n}}$ ${\displaystyle x_{n+1}}$ ${\displaystyle x_{1},\dots ,x_{n}}$ ${\displaystyle x_{k}}$ ${\displaystyle x_{n+1}}$ ${\displaystyle x_{1},\dots ,x_{n}}$ ${\displaystyle x_{n}}$

Los espacios de Hilbert también se utilizan en todos los fundamentos del cálculo de Itô . ^{[63] A cualquier} martingala cuadrada integrable , es posible asociar una norma de Hilbert en el espacio de clases de equivalencia de procesos progresivamente medibles con respecto a la martingala (usando la variación cuadrática de la martingala como medida). La integral de Itô se puede construir definiéndola primero para procesos simples y luego explotando su densidad en el espacio de Hilbert. Un resultado digno de mención es entonces la isometría de Itô , que atestigua que para cualquier martingala M que tenga medida de variación cuadrática , y cualquier proceso progresivamente mensurable H : ${\displaystyle d\langle M\rangle _{t}}$

$${\displaystyle E\left[\left(\int _{0}^{t}H_{s}dM_{s}\right)^{2}\right]=E\left[\int _{0}^{t}H_{s}^{2}d\langle M\rangle _{s}\right]}$$

Una aplicación más profunda de los espacios de Hilbert que es especialmente importante en la teoría de los procesos gaussianos es un intento, debido a Leonard Gross y otros, de dar sentido a ciertas integrales formales en espacios de dimensiones infinitas, como la integral de trayectoria de Feynman de la teoría cuántica de campos . El problema con una integral como esta es que no existe una medida de Lebesgue de dimensión infinita . La noción de un espacio de Wiener abstracto permite construir una medida en un espacio de Banach B que contiene un espacio de Hilbert H , llamado espacio de Cameron-Martin , como un subconjunto denso, a partir de una medida de conjunto de cilindros finitamente aditivo en H. La medida resultante en B es contablemente aditiva e invariante bajo traducción por elementos de H , y esto proporciona una forma matemáticamente rigurosa de pensar la medida de Wiener como una medida gaussiana en el espacio de Sobolev . ^[64] ${\displaystyle H^{1}([0,\infty ))}$

Percepción del color

Cualquier color físico verdadero puede representarse mediante una combinación de colores espectrales puros . Como los colores físicos pueden estar compuestos por cualquier número de colores espectrales, el espacio de colores físicos puede representarse adecuadamente mediante un espacio de Hilbert sobre colores espectrales. Los seres humanos tenemos tres tipos de células cónicas para la percepción del color, por lo que los colores perceptibles pueden representarse mediante un espacio euclidiano tridimensional. El mapeo lineal de muchos a uno del espacio de Hilbert de colores físicos al espacio euclidiano de colores perceptibles por el ser humano explica por qué los humanos pueden percibir muchos colores físicos distintos como idénticos (por ejemplo, luz amarilla pura versus una mezcla de rojo y verde). luz, ver metamerismo ). ^{[65] [66]}

Propiedades

Identidad pitagórica

Dos vectores u y v en un espacio de Hilbert H son ortogonales cuando ⟨ u , v ⟩ = 0 . La notación para esto es u ⊥ v . De manera más general, cuando S es un subconjunto en H , la notación u ⊥ S significa que u es ortogonal a cada elemento de S.

Cuando u y v son ortogonales, se tiene

$${\displaystyle \|u+v\|^{2}=\langle u+v,u+v\rangle =\langle u,u\rangle +2\,\operatorname {Re} \langle u,v\rangle +\langle v,v\rangle =\|u\|^{2}+\|v\|^{2}\,.}$$

Por inducción en n , esto se extiende a cualquier familia u ₁ , ..., u _n de n vectores ortogonales,

$${\displaystyle \left\|u_{1}+\cdots +u_{n}\right\|^{2}=\left\|u_{1}\right\|^{2}+\cdots +\left\|u_{n}\right\|^{2}.}$$

Mientras que la identidad pitagórica tal como se establece es válida en cualquier espacio producto interno, se requiere integridad para la extensión de la identidad pitagórica a las series. ^[67] Una serie Σ u _k de vectores ortogonales converge en H si y sólo si la serie de cuadrados de normas converge, y

$${\displaystyle {\Biggl \|}\sum _{k=0}^{\infty }u_{k}{\Biggr \|}^{2}=\sum _{k=0}^{\infty }\left\|u_{k}\right\|^{2}\,.}$$

Identidad y polarización del paralelogramo.

Geométricamente, la identidad del paralelogramo afirma que AC ² + BD ² = 2(AB ² + AD ² ) . En palabras, la suma de los cuadrados de las diagonales es el doble de la suma de los cuadrados de dos lados adyacentes cualesquiera.

Por definición, todo espacio de Hilbert es también un espacio de Banach . Además, en cada espacio de Hilbert se cumple la siguiente identidad de paralelogramo : ^[68]

$${\displaystyle \|u+v\|^{2}+\|u-v\|^{2}=2{\bigl (}\|u\|^{2}+\|v\|^{2}{\bigr )}\,.}$$

Por el contrario, cada espacio de Banach en el que se cumple la identidad del paralelogramo es un espacio de Hilbert, y el producto interno está determinado únicamente por la norma de la identidad de polarización . ^[69] Para espacios reales de Hilbert, la identidad de polarización es

$${\displaystyle \langle u,v\rangle ={\tfrac {1}{4}}{\bigl (}\|u+v\|^{2}-\|u-v\|^{2}{\bigr )}\,.}$$

Para espacios de Hilbert complejos, es

$${\displaystyle \langle u,v\rangle ={\tfrac {1}{4}}{\bigl (}\|u+v\|^{2}-\|u-v\|^{2}+i\|u+iv\|^{2}-i\|u-iv\|^{2}{\bigr )}\,.}$$

La ley del paralelogramo implica que cualquier espacio de Hilbert es un espacio de Banach uniformemente convexo . ^[70]

Mejor aproximación

Esta subsección emplea el teorema de proyección de Hilbert . Si C es un subconjunto convexo cerrado no vacío de un espacio de Hilbert H y x es un punto en H , existe un punto único y ∈ C que minimiza la distancia entre x y los puntos en C , ^[71]

$${\displaystyle y\in C\,,\quad \|x-y\|=\operatorname {dist} (x,C)=\min {\bigl \{}\|x-z\|\mathrel {\big |} z\in C{\bigr \}}\,.}$$

Esto equivale a decir que hay un punto con norma mínima en el conjunto convexo trasladado D = C − x . La prueba consiste en mostrar que toda secuencia minimizadora ( d _n ) ⊂ D es Cauchy (usando la identidad del paralelogramo) y por lo tanto converge (usando la completitud) a un punto en D que tiene norma mínima. De manera más general, esto se cumple en cualquier espacio de Banach uniformemente convexo. ^[72]

Cuando este resultado se aplica a un subespacio cerrado F de H , se puede demostrar que el punto y ∈ F más cercano a x se caracteriza por ^[73]

$${\displaystyle y\in F\,,\quad x-y\perp F\,.}$$

Este punto y es la proyección ortogonal de x sobre F , y la aplicación P _F  : x → y es lineal (ver Complementos y proyecciones ortogonales). Este resultado es especialmente significativo en matemáticas aplicadas , especialmente en análisis numérico , donde forma la base de los métodos de mínimos cuadrados . ^[74]

En particular, cuando F no es igual a H , se puede encontrar un vector v distinto de cero ortogonal a F (seleccione x ∉ F y v = x − y ). Se obtiene un criterio muy útil aplicando esta observación al subespacio cerrado F generado por un subconjunto S de H.

Un subconjunto S de H abarca un subespacio vectorial denso si (y sólo si) el vector 0 es el único vector v ∈ H ortogonal a S.

Dualidad

El espacio dual H * es el espacio de todas las funciones lineales continuas desde el espacio H hasta el campo base. Lleva consigo una norma natural, definida por

$${\displaystyle \|\varphi \|=\sup _{\|x\|=1,x\in H}|\varphi (x)|\,.}$$

ley del paralelogramoidentidad de polarizacióne _• = ( e _i ) _{i ∈ I}H ${\displaystyle f,g\in H^{*}}$

$${\displaystyle \langle f,g\rangle _{H^{*}}=\sum _{i\in I}f(e_{i}){\overline {g(e_{i})}}}$$

El teorema de representación de Riesz proporciona una descripción conveniente del espacio dual. Para cada elemento u de H , existe un único elemento φ _u de H * , definido por

$${\displaystyle \varphi _{u}(x)=\langle x,u\rangle }$$

${\displaystyle \left\|\varphi _{u}\right\|=\left\|u\right\|.}$

El teorema de representación de Riesz establece que el mapa de H a H * definido por u ↦ φ _u es sobreyectivo , lo que hace de este mapa un isomorfismo antilineal isométrico . ^[75] Entonces, para cada elemento φ del dual H * existe uno y solo un u _φ en H tal que

$${\displaystyle \langle x,u_{\varphi }\rangle =\varphi (x)}$$

x ∈ HH *

$${\displaystyle \langle \varphi ,\psi \rangle =\langle u_{\psi },u_{\varphi }\rangle \,.}$$

La inversión de orden en el lado derecho restaura la linealidad en φ a partir de la antilinealidad de u _φ . En el caso real, el isomorfismo antilineal de H a su dual es en realidad un isomorfismo, por lo que los espacios reales de Hilbert son naturalmente isomorfos a sus propios duales.

El vector representativo u _φ se obtiene de la siguiente manera. Cuando φ ≠ 0 , el núcleo F = Ker( φ ) es un subespacio vectorial cerrado de H , no igual a H , por lo tanto , existe un vector v distinto de cero ortogonal a F. El vector u es un múltiplo escalar adecuado λv de v . El requisito de que φ ( v ) = ⟨ v , u ⟩ produce

$${\displaystyle u=\langle v,v\rangle ^{-1}\,{\overline {\varphi (v)}}\,v\,.}$$

Esta correspondencia φ ↔ u es explotada por la notación de soporte popular en física . ^[76] Es común en física suponer que el producto interno, denotado por ⟨ x | y ⟩ , es lineal a la derecha,

$${\displaystyle \langle x|y\rangle =\langle y,x\rangle \,.}$$

⟨ x | y ⟩⟨ x | sujetador| y ⟩ket

El teorema de representación de Riesz se basa fundamentalmente no sólo en la presencia de un producto interno, sino también en la integridad del espacio. De hecho, el teorema implica que el dual topológico de cualquier espacio producto interno puede identificarse con su compleción. ^[77] Una consecuencia inmediata del teorema de representación de Riesz es también que un espacio de Hilbert H es reflexivo , lo que significa que el mapa natural de H en su doble espacio dual es un isomorfismo.

Secuencias débilmente convergentes

En un espacio de Hilbert H , una secuencia { x _n } es débilmente convergente a un vector x ∈ H cuando

$${\displaystyle \lim _{n}\langle x_{n},v\rangle =\langle x,v\rangle }$$

v ∈ H

Por ejemplo, cualquier secuencia ortonormal { f _n } converge débilmente a 0, como consecuencia de la desigualdad de Bessel. Cada secuencia débilmente convergente { x _n } está acotada por el principio de acotación uniforme .

Por el contrario, toda secuencia acotada en un espacio de Hilbert admite subsecuencias débilmente convergentes ( teorema de Alaoglu ). ^[78] Este hecho puede usarse para probar resultados de minimización para funcionales convexos continuos , de la misma manera que el teorema de Bolzano-Weierstrass se usa para funciones continuas en R ^d . Entre varias variantes, una afirmación sencilla es la siguiente: ^[79]

Si f  : H → R es una función continua convexa tal que f ( x ) tiende a +∞ cuando ‖ x ‖ tiende a ∞ , entonces f admite un mínimo en algún punto x ₀ ∈ H .

Este hecho (y sus diversas generalizaciones) son fundamentales para los métodos directos en el cálculo de variaciones . Los resultados de minimización para funcionales convexos también son una consecuencia directa del hecho ligeramente más abstracto de que los subconjuntos convexos acotados cerrados en un espacio de Hilbert H son débilmente compactos , ya que H es reflexivo. La existencia de subsecuencias débilmente convergentes es un caso especial del teorema de Eberlein-Šmulian .

Propiedades del espacio de Banach

Cualquier propiedad general de los espacios de Banach sigue siendo válida para los espacios de Hilbert. El teorema de mapeo abierto establece que una transformación lineal sobreyectiva continua de un espacio de Banach a otro es un mapeo abierto, lo que significa que envía conjuntos abiertos a conjuntos abiertos. Un corolario es el teorema de la inversa acotada , de que una función lineal continua y biyectiva de un espacio de Banach a otro es un isomorfismo (es decir, una aplicación lineal continua cuya inversa también es continua). Este teorema es considerablemente más sencillo de demostrar en el caso de los espacios de Hilbert que en el de los espacios de Banach en general. ^[80] El teorema de mapeo abierto es equivalente al teorema del gráfico cerrado , que afirma que una función lineal de un espacio de Banach a otro es continua si y solo si su gráfico es un conjunto cerrado . ^[81] En el caso de los espacios de Hilbert, esto es básico en el estudio de operadores ilimitados (ver operador cerrado ).

El teorema (geométrico) de Hahn-Banach afirma que un conjunto convexo cerrado puede separarse de cualquier punto exterior a él mediante un hiperplano del espacio de Hilbert. Esta es una consecuencia inmediata de la propiedad de mejor aproximación: si y es el elemento de un conjunto convexo cerrado F más cercano a x , entonces el hiperplano de separación es el plano perpendicular al segmento xy que pasa por su punto medio. ^[82]

Operadores en espacios de Hilbert

Operadores acotados

Los operadores lineales continuos A  : H ₁ → H ₂ desde un espacio de Hilbert H ₁ a un segundo espacio de Hilbert H ₂ están acotados en el sentido de que asignan conjuntos acotados a conjuntos acotados. ^[83] Por el contrario, si un operador está acotado, entonces es continuo. El espacio de tales operadores lineales acotados tiene una norma , la norma del operador dada por

$${\displaystyle \lVert A\rVert =\sup {\bigl \{}\|Ax\|\mathrel {\big |} \|x\|\leq 1{\bigr \}}\,.}$$

La suma y el compuesto de dos operadores lineales acotados son nuevamente acotados y lineales. Para y en H ₂ , el mapa que envía x ∈ H ₁ a ⟨ Ax , y ⟩ es lineal y continuo y, según el teorema de representación de Riesz, puede representarse en la forma

$${\displaystyle \left\langle x,A^{*}y\right\rangle =\langle Ax,y\rangle }$$

A * yH ₁A * : H ₂ → H ₁adjuntoAA ** = AA es idéntico atranspuesta ^t A  : H ₂ * → H ₁ *A ${\displaystyle \psi \in H_{2}^{*}}$ ${\displaystyle \psi \circ A\in H_{1}^{*}.}$

El conjunto B( H ) de todos los operadores lineales acotados en H (es decir, operadores H → H ), junto con las operaciones de suma y composición, la norma y la operación adjunta, es un álgebra C* , que es un tipo de álgebra de operadores. .

Un elemento A de B( H ) se llama 'autoadjunto' o 'hermitiano' si A * = A . Si A es hermitiano y ⟨ Ax , x ⟩ ≥ 0 para cada x , entonces A se llama 'no negativo', escrito A ≥ 0 ; Si la igualdad se cumple sólo cuando x = 0 , entonces A se llama "positiva". El conjunto de operadores autoadjuntos admite un orden parcial , en el que A ≥ B si A − B ≥ 0 . Si A tiene la forma B * B para algún B , entonces A no es negativo; si B es invertible, entonces A es positivo. Lo contrario también es cierto en el sentido de que, para un operador no negativo A , existe una única raíz cuadrada no negativa B tal que

$${\displaystyle A=B^{2}=B^{*}B\,.}$$

En un sentido precisado por el teorema espectral , los operadores autoadjuntos pueden considerarse operadores "reales". Un elemento A de B( H ) se llama normal si A * A = AA * . Los operadores normales se descomponen en la suma de un operador autoadjunto y un múltiplo imaginario de un operador autoadjunto

$${\displaystyle A={\frac {A+A^{*}}{2}}+i{\frac {A-A^{*}}{2i}}}$$

Un elemento U de B( H ) se llama unitario si U es invertible y su inversa está dada por U * . Esto también se puede expresar requiriendo que U sea sobre y ⟨ Ux , Uy ⟩ = ⟨ x , y ⟩ para todo x , y ∈ H. Los operadores unitarios forman un grupo bajo composición, que es el grupo de isometría de H.

Un elemento de B( H ) es compacto si envía conjuntos acotados a conjuntos relativamente compactos . De manera equivalente, un operador acotado T es compacto si, para cualquier secuencia acotada { x _k } , la secuencia { Tx _k } tiene una subsecuencia convergente. Muchos operadores integrales son compactos y, de hecho, definen una clase especial de operadores conocidos como operadores de Hilbert-Schmidt que son especialmente importantes en el estudio de ecuaciones integrales . Los operadores de Fredholm se diferencian de un operador compacto por un múltiplo de la identidad y se caracterizan de manera equivalente como operadores con un núcleo y un cokernel de dimensión finita . El índice de un operador de Fredholm T está definido por

$${\displaystyle \operatorname {index} T=\dim \ker T-\dim \operatorname {coker} T\,.}$$

El índice es invariante de homotopía y juega un papel profundo en la geometría diferencial a través del teorema del índice de Atiyah-Singer .

Operadores ilimitados

Los operadores ilimitados también son manejables en espacios de Hilbert y tienen importantes aplicaciones en la mecánica cuántica . ^[84] Un operador ilimitado T en un espacio de Hilbert H se define como un operador lineal cuyo dominio D ( T ) es un subespacio lineal de H . A menudo, el dominio D ( T ) es un subespacio denso de H , en cuyo caso T se conoce como operador densamente definido .

El adjunto de un operador ilimitado densamente definido se define esencialmente de la misma manera que para los operadores acotados. Los operadores ilimitados autoadjuntos desempeñan el papel de los observables en la formulación matemática de la mecánica cuántica. Ejemplos de operadores ilimitados autoadjuntos en el espacio de Hilbert L ² ( R ) son: ^[85]

• Una extensión adecuada del operador diferencial.
  $${\displaystyle (Af)(x)=-i{\frac {\mathrm {d} }{\mathrm {d} x}}f(x)\,,}$$
  donde i es la unidad imaginaria y f es una función diferenciable de soporte compacto.
• El operador de multiplicación por x :
  $${\displaystyle (Bf)(x)=xf(x)\,.}$$

Estos corresponden a los observables de impulso y posición , respectivamente. Ni A ni B están definidos en todo H , ya que en el caso de A no es necesario que exista la derivada, y en el caso de B la función producto no necesita ser integrable al cuadrado. En ambos casos, el conjunto de argumentos posibles forman subespacios densos de L ² ( R ) .

Construcciones

sumas directas

Dos espacios de Hilbert H ₁ y H ₂ se pueden combinar en otro espacio de Hilbert, llamado suma directa (ortogonal) , ^[86] y denotado

$${\displaystyle H_{1}\oplus H_{2}\,,}$$

que consta del conjunto de todos los pares ordenados ( x ₁ , x ₂ ) donde x _i ∈ H _i , i = 1, 2 y el producto interno definido por

$${\displaystyle {\bigl \langle }(x_{1},x_{2}),(y_{1},y_{2}){\bigr \rangle }_{H_{1}\oplus H_{2}}=\left\langle x_{1},y_{1}\right\rangle _{H_{1}}+\left\langle x_{2},y_{2}\right\rangle _{H_{2}}\,.}$$

De manera más general, si H _i es una familia de espacios de Hilbert indexados por i ∈ I , entonces la suma directa de H _i , denotada

$${\displaystyle \bigoplus _{i\in I}H_{i}}$$

$${\displaystyle x=(x_{i}\in H_{i}\mid i\in I)\in \prod _{i\in I}H_{i}}$$

producto cartesianoH _i

$${\displaystyle \sum _{i\in I}\|x_{i}\|^{2}<\infty \,.}$$

El producto interior está definido por

$${\displaystyle \langle x,y\rangle =\sum _{i\in I}\left\langle x_{i},y_{i}\right\rangle _{H_{i}}\,.}$$

Cada uno de los _Hi está incluido como un subespacio cerrado en la suma directa de todos _los Hi . Además, los Hi son ortogonales por pares _. Por el contrario, si hay un sistema de subespacios cerrados, Vi _, i ∈ I , en un espacio de Hilbert H , que son ortogonales por pares y cuya unión es densa en H , entonces H es canónicamente isomorfo a la suma directa de Vi _. En este caso, H se llama suma _directa interna del Vi . Una suma directa (interna o externa) también está equipada con una familia de proyecciones ortogonales E _i sobre la i -ésima suma directa H _i . Estas proyecciones son operadores idempotentes , autoadjuntos y acotados que satisfacen la condición de ortogonalidad.

$${\displaystyle E_{i}E_{j}=0,\quad i\neq j\,.}$$

El teorema espectral para operadores compactos autoadjuntos en un espacio de Hilbert H establece que H se divide en una suma directa ortogonal de los espacios propios de un operador y también proporciona una descomposición explícita del operador como una suma de proyecciones sobre los espacios propios. La suma directa de los espacios de Hilbert también aparece en mecánica cuántica como el espacio de Fock de un sistema que contiene un número variable de partículas, donde cada espacio de Hilbert en la suma directa corresponde a un grado adicional de libertad para el sistema de la mecánica cuántica. En teoría de la representación , el teorema de Peter-Weyl garantiza que cualquier representación unitaria de un grupo compacto en un espacio de Hilbert se divide como la suma directa de representaciones de dimensión finita.

Productos tensoriales

Si x ₁ , y ₁ ∊ H ₁ y x ₂ , y ₂ ∊ H ₂ , entonces se define un producto interno en el producto tensorial (ordinario) de la siguiente manera. En tensores simples , dejemos

$${\displaystyle \langle x_{1}\otimes x_{2},\,y_{1}\otimes y_{2}\rangle =\langle x_{1},y_{1}\rangle \,\langle x_{2},y_{2}\rangle \,.}$$

Esta fórmula luego se extiende por sesquilinealidad a un producto interno en H ₁ ⊗ H ₂ . El producto tensorial hilbertiano de H ₁ y H ₂ , a veces denotado como H ₁ H ₂ ${\displaystyle {\widehat {\otimes }}}$ , es el espacio de Hilbert que se obtiene completando H ₁ ⊗ H ₂ para la métrica asociada a este producto interno. ^[87]

Un ejemplo lo proporciona el espacio de Hilbert L ² ([0, 1]) . El producto tensor hilbertiano de dos copias de L ² ([0, 1]) es isométrica y linealmente isomorfo al espacio L ² ([0, 1] ² ) de funciones integrables al cuadrado en el cuadrado [0, 1] ² . Este isomorfismo envía un tensor simple f ₁ ⊗ f ₂ a la función

$${\displaystyle (s,t)\mapsto f_{1}(s)\,f_{2}(t)}$$

Este ejemplo es típico en el siguiente sentido. ^[88] Asociado a cada producto tensorial simple x ₁ ⊗ x ₂ está el operador de rango uno de H^∗
₁a H _​​2 que mapea un x * ∈ H dado^∗
₁como

$${\displaystyle x^{*}\mapsto x^{*}(x_{1})x_{2}\,.}$$

Este mapeo definido en tensores simples se extiende a una identificación lineal entre H ₁ ⊗ H ₂ y el espacio de operadores de rango finito de H^∗
₁a H2 . _{_} Esto se extiende a una isometría lineal del producto tensor hilbertiano H ₁ H ₂ ${\displaystyle {\widehat {\otimes }}}$ con el espacio de Hilbert HS ( H^∗
₁, H ₂ ) de operadores Hilbert-Schmidt de H^∗
₁a H2 . _{_}

Bases ortonormales

La noción de base ortonormal del álgebra lineal se generaliza al caso de los espacios de Hilbert. ^[89] En un espacio de Hilbert H , una base ortonormal es una familia { e _k } _{k ∈ B} de elementos de H que satisfacen las condiciones:

1. Ortogonalidad : Cada dos elementos diferentes de B son ortogonales: ⟨ e _k , e _j ⟩ = 0 para todo k , j ∈ B con k ≠ j .
2. Normalización : Cada elemento de la familia tiene norma 1: ‖ e _k ‖ = 1 para todo k ∈ B .
3. Completitud : El tramo lineal de la familia e _k , k ∈ B , es denso en H.

Un sistema de vectores que satisface las dos primeras condiciones se llama sistema ortonormal o conjunto ortonormal (o secuencia ortonormal si B es contable ). Un sistema así es siempre linealmente independiente .

A pesar del nombre, una base ortonormal no es, en general, una base en el sentido del álgebra lineal ( base de Hamel ). Más precisamente, una base ortonormal es una base de Hamel si y sólo si el espacio de Hilbert es un espacio vectorial de dimensión finita. ^[90]

La completitud de un sistema ortonormal de vectores de un espacio de Hilbert se puede replantear de manera equivalente como:

para cada v ∈ H , si ⟨ v , e _k ⟩ = 0 para todo k ∈ B , entonces v = 0 .

Esto está relacionado con el hecho de que el único vector ortogonal a un subespacio lineal denso es el vector cero, ya que si S es cualquier conjunto ortonormal y v es ortogonal a S , entonces v es ortogonal al cierre del tramo lineal de S , que es todo el espacio.

Ejemplos de bases ortonormales incluyen:

• el conjunto {(1, 0, 0), (0, 1, 0), (0, 0, 1)} forma una base ortonormal de R ³ con el producto escalar ;
• la secuencia {  f _n | n ∈ Z } con f _n ( x ) = exp (2π inx ) forma una base ortonormal del espacio complejo L ² ([0, 1]) ;

En el caso de dimensión infinita, una base ortonormal no será una base en el sentido del álgebra lineal ; Para distinguir las dos, la última base también se llama base de Hamel . Que el tramo de los vectores base sea denso implica que cada vector en el espacio puede escribirse como la suma de una serie infinita, y la ortogonalidad implica que esta descomposición es única.

Espacios de secuencia

El espacio de sucesiones cuadradas sumables de números complejos es el conjunto de sucesiones infinitas ^[9] ${\displaystyle \ell _{2}}$

$${\displaystyle (c_{1},c_{2},c_{3},\dots )}$$

$${\displaystyle \left|c_{1}\right|^{2}+\left|c_{2}\right|^{2}+\left|c_{3}\right|^{2}+\cdots <\infty \,.}$$

Este espacio tiene una base ortonormal:

$${\displaystyle {\begin{aligned}e_{1}&=(1,0,0,\dots )\\e_{2}&=(0,1,0,\dots )\\&\ \ \vdots \end{aligned}}}$$

Este espacio es la generalización de dimensión infinita del espacio de vectores de dimensión finita. Suele ser el primer ejemplo utilizado para mostrar que en espacios de dimensión infinita, un conjunto cerrado y acotado no es necesariamente (secuencialmente) compacto (como es el caso en todos los espacios de dimensión finita ). De hecho, el conjunto de vectores ortonormales anterior muestra esto: es una secuencia infinita de vectores en la bola unitaria (es decir, la bola de puntos con norma menor o igual a uno). Este conjunto está claramente acotado y cerrado; sin embargo, ninguna subsecuencia de estos vectores converge a nada y, en consecuencia, la bola unitaria no es compacta. Intuitivamente, esto se debe a que "siempre hay otra dirección de coordenadas" hacia la cual los siguientes elementos de la secuencia pueden evadir. ${\displaystyle \ell _{2}^{n}}$ ${\displaystyle \ell _{2}}$

Se puede generalizar el espacio de muchas maneras. Por ejemplo, si B es cualquier conjunto, entonces se puede formar un espacio de Hilbert de secuencias con el conjunto de índices B , definido por ^[91] ${\displaystyle \ell _{2}}$

$${\displaystyle \ell ^{2}(B)={\biggl \{}x:B\xrightarrow {x} \mathbb {C} \mathrel {\bigg |} \sum _{b\in B}\left|x(b)\right|^{2}<\infty {\biggr \}}\,.}$$

La suma sobre B se define aquí por

$${\displaystyle \sum _{b\in B}\left|x(b)\right|^{2}=\sup \sum _{n=1}^{N}\left|x(b_{n})\right|^{2}}$$

supremumBl ² ( B )

$${\displaystyle \langle x,y\rangle =\sum _{b\in B}x(b){\overline {y(b)}}}$$

para todo x , y ∈ l ² ( B ) . Aquí la suma también tiene sólo un número contable de términos distintos de cero y es incondicionalmente convergente por la desigualdad de Cauchy-Schwarz.

Una base ortonormal de l ² ( B ) está indexada por el conjunto B , dado por

$${\displaystyle e_{b}(b')={\begin{cases}1&{\text{if }}b=b'\\0&{\text{otherwise.}}\end{cases}}}$$

La desigualdad de Bessel y la fórmula de Parseval

Sea f ₁ , …, f _n un sistema ortonormal finito en  H . Para un vector arbitrario x ∈ H , sea

$${\displaystyle y=\sum _{j=1}^{n}\langle x,f_{j}\rangle \,f_{j}\,.}$$

Entonces ⟨ x , f _k ⟩ = ⟨ y , f _k ⟩ para cada k = 1,…, n . Se deduce que x − y es ortogonal a cada f _k , por lo tanto x − y es ortogonal a  y . Utilizando la identidad pitagórica dos veces, se deduce que

$${\displaystyle \|x\|^{2}=\|x-y\|^{2}+\|y\|^{2}\geq \|y\|^{2}=\sum _{j=1}^{n}{\bigl |}\langle x,f_{j}\rangle {\bigr |}^{2}\,.}$$

Sea { f _i }, i ∈ I , un sistema ortonormal arbitrario en  H . Aplicando la desigualdad anterior a cada subconjunto finito J de I se obtiene la desigualdad de Bessel: ^[92]

$${\displaystyle \sum _{i\in I}{\bigl |}\langle x,f_{i}\rangle {\bigr |}^{2}\leq \|x\|^{2},\quad x\in H}$$

suma de una familia arbitraria

Geométricamente, la desigualdad de Bessel implica que la proyección ortogonal de x sobre el subespacio lineal abarcado por f _i tiene una norma que no excede la de x . En dos dimensiones, esta es la afirmación de que la longitud del cateto de un triángulo rectángulo no puede exceder la longitud de la hipotenusa.

La desigualdad de Bessel es un trampolín hacia el resultado más fuerte llamado identidad de Parseval , que rige el caso en el que la desigualdad de Bessel es en realidad una igualdad. Por definición, si { e _k } _{k ∈ B} es una base ortonormal de H , entonces cada elemento x de H puede escribirse como

$${\displaystyle x=\sum _{k\in B}\left\langle x,e_{k}\right\rangle \,e_{k}\,.}$$

Incluso si B es incontable, la desigualdad de Bessel garantiza que la expresión esté bien definida y consista sólo en un número contable de términos distintos de cero. Esta suma se llama expansión de Fourier de x , y los coeficientes individuales ⟨ x , e _k ⟩ son los coeficientes de Fourier de x . La identidad de Parseval afirma luego que ^[93]

$${\displaystyle \|x\|^{2}=\sum _{k\in B}|\langle x,e_{k}\rangle |^{2}\,.}$$

Por el contrario, ^[93] si { e _k } es un conjunto ortonormal tal que la identidad de Parseval se cumple para cada x , entonces { e _k } es una base ortonormal.

Dimensión de Hilbert

Como consecuencia del lema de Zorn , todo espacio de Hilbert admite una base ortonormal; además, dos bases ortonormales cualesquiera del mismo espacio tienen la misma cardinalidad , llamada dimensión de Hilbert del espacio. ^[94] Por ejemplo, dado que l ² ( B ) tiene una base ortonormal indexada por B , su dimensión de Hilbert es la cardinalidad de B (que puede ser un número entero finito o un número cardinal contable o incontable ).

La dimensión de Hilbert no es mayor que la dimensión de Hamel (la dimensión habitual de un espacio vectorial). Las dos dimensiones son iguales si y sólo una de ellas es finita.

Como consecuencia de la identidad de Parseval, ^[95] si { e _k } _{k ∈ B} es una base ortonormal de H , entonces el mapa Φ : H → l ² ( B ) definido por Φ( x ) = ⟨x, e _k ⟩ _{k ∈ B} es un isomorfismo isométrico de espacios de Hilbert: es un mapeo lineal biyectivo tal que

$${\displaystyle {\bigl \langle }\Phi (x),\Phi (y){\bigr \rangle }_{l^{2}(B)}=\left\langle x,y\right\rangle _{H}}$$

x , y ∈ Hnúmero cardinalBH. l ² ( B )B

Espacios separables

Por definición, un espacio de Hilbert es separable siempre que contenga un subconjunto contable denso. Junto con el lema de Zorn, esto significa que un espacio de Hilbert es separable si y sólo si admite una base ortonormal contable . Por lo tanto, todos los espacios de Hilbert separables de dimensión infinita son isométricamente isomórficos al espacio de secuencia cuadrado-sumable ${\displaystyle \ell ^{2}.}$

En el pasado, a menudo se requería que los espacios de Hilbert fueran separables como parte de la definición. ^[96]

En la teoría cuántica de campos

La mayoría de los espacios utilizados en física son separables y, dado que todos son isomórficos entre sí, a menudo se hace referencia a cualquier espacio de Hilbert separable de dimensión infinita como " el espacio de Hilbert" o simplemente "espacio de Hilbert". ^[97] Incluso en la teoría cuántica de campos , la mayoría de los espacios de Hilbert son de hecho separables, como lo estipulan los axiomas de Wightman . Sin embargo, a veces se argumenta que los espacios de Hilbert no separables también son importantes en la teoría cuántica de campos, aproximadamente porque los sistemas en la teoría poseen un número infinito de grados de libertad y cualquier producto tensor de Hilbert infinito (de espacios de dimensión mayor que uno). es inseparable. ^[98] Por ejemplo, un campo bosónico puede considerarse naturalmente como un elemento de un producto tensorial cuyos factores representan osciladores armónicos en cada punto del espacio. Desde esta perspectiva, el espacio de estados naturales de un bosón podría parecer un espacio inseparable. ^[98] Sin embargo, es sólo un pequeño subespacio separable del producto tensorial completo el que puede contener campos físicamente significativos (en los que se pueden definir los observables). Otro espacio de Hilbert no separable modela el estado de una colección infinita de partículas en una región ilimitada del espacio. Una base ortonormal del espacio está indexada por la densidad de las partículas, un parámetro continuo, y como el conjunto de densidades posibles es incontable, la base no es contable. ^[98]

Complementos y proyecciones ortogonales.

Si S es un subconjunto de un espacio de Hilbert H , el conjunto de vectores ortogonales a S está definido por

$${\displaystyle S^{\perp }=\left\{x\in H\mid \langle x,s\rangle =0\ {\text{ for all }}s\in S\right\}\,.}$$

El conjunto S ^⊥ es un subespacio cerrado de H (se puede demostrar fácilmente usando la linealidad y continuidad del producto interno) y por eso forma un espacio de Hilbert. Si V es un subespacio cerrado de H , entonces V ^⊥ se llama complemento ortogonal de V. De hecho, cada x ∈ H puede escribirse únicamente como x = v + w , con v ∈ V y w ∈ V ^⊥ . Por lo tanto, H es la suma directa interna de Hilbert de V y V ^⊥ .

El operador lineal P _V  : H → H que asigna x a v se llama proyección ortogonal sobre V . Existe una correspondencia natural uno a uno entre el conjunto de todos los subespacios cerrados de H y el conjunto de todos los operadores autoadjuntos acotados P tal que P ² = P . Específicamente,

Teorema  :  la proyección ortogonal P _V es un operador lineal autoadjunto en H de norma ≤ 1 con la propiedad P^2V
_{_}= PV . _{_} Además, cualquier operador lineal autoadjunto E tal que E ² = E es de la forma PV , donde _V es el rango de E. Para cada x en H , P _V ( x ) es el único elemento v de V que minimiza la distancia ‖ x − v ‖ .

Esto proporciona la interpretación geométrica de P _V ( x ) : es la mejor aproximación a x por elementos de V. ^[99]

Las proyecciones P _U y P _V se llaman mutuamente ortogonales si P _U P _V = 0 . Esto equivale a que U y V sean ortogonales como subespacios de H. La suma de las dos proyecciones PU y PV es una proyección solo si _U y V son ortogonales entre sí, _{y en ese caso} PU + PV = PU _{+ V.} ^[100] El compuesto P _U P _V generalmente no es una proyección; de hecho, el compuesto es una proyección si y sólo si las dos proyecciones conmutan, y en ese caso P _U P _V = P _{U ∩ V} . ^[101]

Al restringir el codominio al espacio de Hilbert V , la proyección ortogonal _PV da lugar a una proyección de mapeo π  : H → V ; es el adjunto del mapeo de inclusión

$${\displaystyle i:V\to H\,,}$$

$${\displaystyle \left\langle ix,y\right\rangle _{H}=\left\langle x,\pi y\right\rangle _{V}}$$

x ∈ Vy ∈ H

La norma del operador de la proyección ortogonal P _V sobre un subespacio cerrado V distinto de cero es igual a 1:

$${\displaystyle \|P_{V}\|=\sup _{x\in H,x\neq 0}{\frac {\|P_{V}x\|}{\|x\|}}=1\,.}$$

Todo subespacio cerrado V de un espacio de Hilbert es, por tanto, la imagen de un operador P de norma uno tal que P ² = P . La propiedad de poseer operadores de proyección apropiados caracteriza los espacios de Hilbert: ^[102]

• Un espacio de Banach de dimensión superior a 2 es (isométricamente) un espacio de Hilbert si y sólo si, para cada subespacio cerrado V , existe un operador PV de norma uno cuya imagen es V tal que _P^2V
  _{_}= PV . _{_}

Si bien este resultado caracteriza la estructura métrica de un espacio de Hilbert, la estructura de un espacio de Hilbert como espacio vectorial topológico puede caracterizarse en términos de la presencia de subespacios complementarios: ^[103]

• Un espacio de Banach X es topológica y linealmente isomorfo a un espacio de Hilbert si y sólo si, para cada subespacio cerrado V , existe un subespacio cerrado W tal que X es igual a la suma directa interna V ⊕ W.

El complemento ortogonal satisface algunos resultados más elementales. Es una función monótona en el sentido de que si U ⊂ V , entonces V ^⊥ ⊆ U ^⊥ con igualdad si y solo si V está contenido en la clausura de U . Este resultado es un caso especial del teorema de Hahn-Banach . La clausura de un subespacio se puede caracterizar completamente en términos del complemento ortogonal: si V es un subespacio de H , entonces la clausura de V es igual a V ^⊥⊥ . El complemento ortogonal es, por tanto, una conexión de Galois en el orden parcial de los subespacios de un espacio de Hilbert. En general, el complemento ortogonal de una suma de subespacios es la intersección de los complementos ortogonales: ^[104]

$${\displaystyle {\biggl (}\sum _{i}V_{i}{\biggr )}^{\perp }=\bigcap _{i}V_{i}^{\perp }\,.}$$

Si los V _i además están cerrados, entonces

$${\displaystyle {\overline {\sum _{i}V_{i}^{\perp }}}={\biggl (}\bigcap _{i}V_{i}{\biggr )}^{\perp }\,.}$$

Teoría espectral

Existe una teoría espectral bien desarrollada para operadores autoadjuntos en un espacio de Hilbert, que es más o menos análoga al estudio de matrices simétricas sobre los reales o matrices autoadjuntas sobre números complejos. ^[105] En el mismo sentido, se puede obtener una "diagonalización" de un operador autoadjunto como una suma adecuada (en realidad una integral) de operadores de proyección ortogonales.

El espectro de un operador T , denotado σ ( T ) , es el conjunto de números complejos λ tales que T − λ carece de inverso continuo. Si T está acotado, entonces el espectro es siempre un conjunto compacto en el plano complejo y se encuentra dentro del disco | z | ≤ ‖ T ‖ . Si T es autoadjunto, entonces el espectro es real. De hecho, está contenido en el intervalo [ m , M ] donde

$${\displaystyle m=\inf _{\|x\|=1}\langle Tx,x\rangle \,,\quad M=\sup _{\|x\|=1}\langle Tx,x\rangle \,.}$$

Además, m y M están realmente contenidos dentro del espectro.

Los espacios propios de un operador T están dados por

$${\displaystyle H_{\lambda }=\ker(T-\lambda )\,.}$$

A diferencia de las matrices finitas, no todos los elementos del espectro de T deben ser un valor propio: al operador lineal T − λ solo le puede faltar una inversa porque no es sobreyectivo. Los elementos del espectro de un operador en sentido general se conocen como valores espectrales . Dado que los valores espectrales no tienen por qué ser valores propios, la descomposición espectral suele ser más sutil que en dimensiones finitas.

Sin embargo, el teorema espectral de un operador autoadjunto T toma una forma particularmente simple si, además, se supone que T es un operador compacto . El teorema espectral para operadores compactos autoadjuntos establece: ^[106]

• Un operador autoadjunto compacto T tiene solo un número contable (o finito) de valores espectrales. El espectro de T no tiene punto límite en el plano complejo excepto posiblemente cero. Los espacios propios de T descomponen H en una suma directa ortogonal:
  $${\displaystyle H=\bigoplus _{\lambda \in \sigma (T)}H_{\lambda }\,.}$$
  Además, si E _λ denota la proyección ortogonal sobre el espacio propio H _λ , entonces
  $${\displaystyle T=\sum _{\lambda \in \sigma (T)}\lambda E_{\lambda }\,,}$$
  donde la suma converge con respecto a la norma en B( H ) .

Este teorema juega un papel fundamental en la teoría de ecuaciones integrales , pues muchos operadores integrales son compactos, en particular los que surgen de los operadores de Hilbert-Schmidt .

El teorema espectral general para operadores autoadjuntos implica una especie de integral de Riemann-Stieltjes valorada por el operador , en lugar de una suma infinita. ^[107] La ​​familia espectral asociada a T asocia a cada número real λ un operador E _λ , que es la proyección sobre el espacio nulo del operador ( T − λ ) ⁺ , donde la parte positiva de un operador autoadjunto está definida por

$${\displaystyle A^{+}={\tfrac {1}{2}}{\Bigl (}{\sqrt {A^{2}}}+A{\Bigr )}\,.}$$

Los operadores E _λ son monótonos crecientes con respecto al orden parcial definido en los operadores autoadjuntos; los valores propios corresponden precisamente a las discontinuidades de salto. Se tiene el teorema espectral, que afirma

$${\displaystyle T=\int _{\mathbb {R} }\lambda \,\mathrm {d} E_{\lambda }\,.}$$

La integral se entiende como una integral de Riemann-Stieltjes, convergente respecto de la norma sobre B( H ) . En particular, se tiene la representación integral ordinaria con valores escalares

$${\displaystyle \langle Tx,y\rangle =\int _{\mathbb {R} }\lambda \,\mathrm {d} \langle E_{\lambda }x,y\rangle \,.}$$

Una descomposición espectral algo similar es válida para los operadores normales, aunque debido a que el espectro ahora puede contener números complejos no reales, la medida de Stieltjes valorada por el operador d E _λ debe reemplazarse por una resolución de la identidad .

Una aplicación importante de los métodos espectrales es el teorema de mapeo espectral , que permite aplicar a un operador autoadjunto T cualquier función compleja continua f definida en el espectro de T formando la integral

$${\displaystyle f(T)=\int _{\sigma (T)}f(\lambda )\,\mathrm {d} E_{\lambda }\,.}$$

El cálculo funcional continuo resultante tiene aplicaciones en particular para operadores pseudodiferenciales . ^[108]

La teoría espectral de los operadores autoadjuntos ilimitados es sólo marginalmente más difícil que la de los operadores acotados. El espectro de un operador ilimitado se define exactamente de la misma manera que para los operadores acotados: λ es un valor espectral si el operador resolutivo

$${\displaystyle R_{\lambda }=(T-\lambda )^{-1}}$$

no logra ser un operador continuo bien definido. La autoadjunción de T todavía garantiza que el espectro sea real. Por lo tanto, la idea esencial de trabajar con operadores ilimitados es mirar el resolutivo R _λ donde λ es irreal. Este es un operador normal acotado , que admite una representación espectral que luego puede transferirse a una representación espectral de T mismo. Se utiliza una estrategia similar, por ejemplo, para estudiar el espectro del operador de Laplace: en lugar de dirigirse al operador directamente, se busca un resolutivo asociado, como un potencial de Riesz o un potencial de Bessel .

Una versión precisa del teorema espectral en este caso es: ^[109]

Teorema  :  dado un operador autoadjunto densamente definido T en un espacio de Hilbert H , corresponde una resolución única de la identidad E en los conjuntos de Borel de R , tal que

$${\displaystyle \langle Tx,y\rangle =\int _{\mathbb {R} }\lambda \,\mathrm {d} E_{x,y}(\lambda )}$$

para todo x ∈ D ( T ) y y ∈ H . La medida espectral E se concentra en el espectro de T .

También existe una versión del teorema espectral que se aplica a operadores normales ilimitados.

En la cultura popular

En Gravity's Rainbow (1973), una novela de Thomas Pynchon , uno de los personajes se llama "Sammy Hilbert-Spaess", un juego de palabras con "Hilbert Space". La novela también se refiere a los teoremas de incompletitud de Gödel . ^[110]

Ver también

• Portal de matemáticas

• Espacio de Banach  : espacio vectorial normado que está completo
• Espacio Fock  - Espacio de estados de múltiples partículas
• Teorema fundamental de los espacios de Hilbert
• Espacio Hadamard  : espacio métrico geodésicamente completo de curvatura no positivaPages displaying wikidata descriptions as a fallback
• Espacio de Hausdorff  - Tipo de espacio topológico
• Álgebra de Hilbert
• Módulo Hilbert C*  : objetos matemáticos que generalizan la noción de espacios de Hilbert
• Colector de Hilbert  : colector modelado en espacios de Hilbert
• Producto L-semi-interior  : generalización de productos interiores que se aplica a todos los espacios normados.
• Espacio vectorial topológico localmente convexo  : un espacio vectorial con una topología definida por conjuntos abiertos convexos
• Teoría del operador  - Campo de estudio matemático
• Topologías de operadores  : topologías en el conjunto de operadores en un espacio de Hilbert
• Espacio de estados cuánticos  : espacio matemático que representa sistemas cuánticos físicos
• Espacio de Hilbert aparejado  : construcción que vincula el estudio de valores propios "ligados" y continuos en el análisis funcional
• Espacio vectorial topológico  : espacio vectorial con noción de cercanía

Observaciones

1. En algunas convenciones, los productos internos son lineales en sus segundos argumentos.
2. Los valores propios del núcleo de Fredholm son1/λ, que tienden a cero.

Notas

1. Axler 2014, pag. 164 §6.2
2. Sin embargo, algunas fuentes llaman espacios de dimensión finita con estas propiedades espacios anteriores a Hilbert, reservando el término "espacio de Hilbert" para espacios de dimensión infinita; ver, por ejemplo, Levitan 2001.
3. Marsden 1974, §2.8
4. El material matemático de esta sección se puede encontrar en cualquier buen libro de texto sobre análisis funcional, como Dieudonné (1960), Hewitt & Stromberg (1965), Reed & Simon (1980) o Rudin (1987).
5. Schaefer y Wolff 1999, págs. 122-202.
6. Dieudonné 1960, §6.2
7. Romano 2008, pag. 327
8. Romano 2008, pag. 330 Teorema 13.8
9. Stein y Shakarchi 2005, pág. 163}}
10. Dieudonné 1960
11. En gran parte del trabajo de Hermann Grassmann , a instancias de August Ferdinand Möbius (Boyer & Merzbach 1991, págs. 584–586). La primera explicación axiomática moderna de los espacios vectoriales abstractos apareció finalmente en la de Giuseppe Peano de 1888 (Grattan-Guinness 2000, §5.2.2; O'Connor & Robertson 1996).
12. Se puede encontrar un relato detallado de la historia de los espacios de Hilbert en Bourbaki 1987.
13. Schmidt 1908
14. Titchmarsh 1946, §IX.1
15. Lebesgue 1904. Se pueden encontrar más detalles sobre la historia de la teoría de la integración en Bourbaki (1987) y Saks (2005).
16. Bourbaki 1987.
17. Dunford y Schwartz 1958, §IV.16
18. En Dunford & Schwartz (1958, §IV.16), el resultado de que cada funcional lineal en L ² [0,1] está representado por integración se atribuye conjuntamente a Fréchet (1907) y Riesz (1907). El resultado general, que el dual de un espacio de Hilbert se identifica con el propio espacio de Hilbert, se puede encontrar en Riesz (1934).
19. Von Neumann 1929.
20. Kline 1972, pag. 1092
21. Hilbert, Nordheim y von Neumann 1927
22. Weyl 1931.
23. Prugovečki 1981, págs. 1-10.
24. von Neumann 1932
25. Peres 1993, págs. 79–99.
26. Murphy 1990, pag. 112
27. Murphy 1990, pag. 72
28. Halmos 1957, artículo 42.
29. Hewitt y Stromberg 1965.
30. Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [junio de 1964]. "Capítulo 22". Manual de funciones matemáticas con fórmulas, gráficas y tablas matemáticas . Serie de Matemáticas Aplicadas. vol. 55 (Novena reimpresión con correcciones adicionales de la décima impresión original con correcciones (diciembre de 1972); primera ed.). Washington DC; Nueva York: Departamento de Comercio de los Estados Unidos, Oficina Nacional de Normas; Publicaciones de Dover. pag. 773.ISBN _ 978-0-486-61272-0. LCCN  64-60036. SEÑOR  0167642. LCCN  65-12253.
31. Bers, John y Schechter 1981.
32. Giusti 2003.
33. Stein 1970
34. Los detalles se pueden encontrar en Warner (1983).
35. Una referencia general sobre los espacios de Hardy es el libro Duren (1970).
36. Krantz 2002, §1.4
37. Krantz 2002, §1.5
38. Joven 1988, Capítulo 9.
39. Pedersen 1995, §4.4
40. Se pueden encontrar más detalles sobre los métodos de elementos finitos desde este punto de vista en Brenner y Scott (2005).
41. Brezis 2010, sección 9.5
42. Evans 1998
43. Pathria (1996), capítulos 2 y 3
44. Einsiedler & Ward (2011), Proposición 2.14.
45. Caña y Simón 1980
46. Un tratamiento de las series de Fourier desde este punto de vista está disponible, por ejemplo, en Rudin (1987) o Folland (2009).
47. Halmos 1957, §5
48. Bachman, Narici y Beckenstein 2000
49. Stein y Weiss 1971, §IV.2.
50. Lanczos 1988, págs. 212-213
51. Lanczos 1988, Ecuación 4-3.10
52. La referencia clásica para los métodos espectrales es Courant & Hilbert 1953. Un relato más actualizado es Reed & Simon 1975.
53. Kac 1966
54. Von Neumann 1955
55. Holevo 2001, pag. 17
56. Rieffel y Polak 2011, pág. 55
57. Peres 1993, pag. 101
58. Peres 1993, págs.73
59. Nielsen y Chuang 2000, pág. 90
60. Billingsley (1986), pág. 477, ej. 34.13}}
61. Stapleton 1995
62. Hewitt y Stromberg (1965), Ejercicio 16.45.
63. Karatzas y Shreve 2019, Capítulo 3
64. Stroock (2011), Capítulo 8.
65. Hermann Weyl (2009), "Mente y naturaleza", Mente y naturaleza: escritos seleccionados sobre filosofía, matemáticas y física , Princeton University Press.
66. Berthier, M. (2020), "Geometría de la percepción del color. Parte 2: colores percibidos a partir de estados cuánticos reales y rebit de Hering", The Journal of Mathematical Neuroscience , 10 (1): 14, doi : 10.1186/s13408-020- 00092-x , PMC 7481323 , PMID  32902776 .
67. Reed y Simon 1980, teorema 12.6
68. Reed y Simon 1980, pág. 38
69. Joven 1988, pag. 23.
70. Clarkson 1936.
71. Rudin 1987, Teorema 4.10
72. Dunford y Schwartz 1958, II.4.29
73. Rudin 1987, Teorema 4.11
74. Blanchet, Gerard; Charbit, Maurice (2014). Procesamiento de imágenes y señales digitales mediante MATLAB . vol. 1 (Segunda ed.). Nueva Jersey: Wiley. págs. 349–360. ISBN 978-1848216402.
75. Weidmann 1980, Teorema 4.8
76. Peres 1993, págs. 77–78.
77. Weidmann (1980), Ejercicio 4.11.
78. Weidmann 1980, §4.5
79. Buttazzo, Giaquinta y Hildebrandt 1998, Teorema 5.17
80. Halmos 1982, Problema 52, 58
81. Rudin 1973
82. Trèves 1967, Capítulo 18
83. Una referencia general para esta sección es Rudin (1973), capítulo 12.
84. Véase Prugovečki (1981), Reed & Simon (1980, Capítulo VIII) y Folland (1989).
85. Prugovečki 1981, III, §1.4
86. Dunford y Schwartz 1958, IV.4.17-18
87. Weidmann 1980, §3.4
88. Kadison y Ringrose 1983, Teorema 2.6.4
89. Dunford y Schwartz 1958, §IV.4.
90. Romano 2008, pag. 218
91. Rudin 1987, Definición 3.7
92. Para el caso de conjuntos de índices finitos, consulte, por ejemplo, Halmos 1957, §5. Para conjuntos de índices infinitos, consulte Weidmann 1980, Teorema 3.6.
93. Hewitt y Stromberg (1965), Teorema 16.26.
94. Levitan 2001. Muchos autores, como Dunford y Schwartz (1958, §IV.4), se refieren a esto simplemente como la dimensión. A menos que el espacio de Hilbert sea de dimensión finita, esto no es lo mismo que su dimensión como espacio lineal (la cardinalidad de una base de Hamel).
95. Hewitt y Stromberg (1965), Teorema 16.29.
96. Prugovečki 1981, I, §4.2
97. von Neumann (1955) define un espacio de Hilbert mediante una base de Hilbert contable, lo que equivale a un isomorfismo isométrico con l ² . La convención aún persiste en los tratamientos más rigurosos de la mecánica cuántica; ver, por ejemplo, Sobrino 1996, Apéndice B.
98. Streater y Wightman 1964, págs. 86–87
99. Joven 1988, Teorema 15.3
100. von Neumann 1955, teorema 16
101. von Neumann 1955, teorema 14
102. Kakutani 1939
103. Lindenstrauss y Tzafriri 1971
104. Halmos 1957, §12
105. Se puede encontrar una descripción general de la teoría espectral en espacios de Hilbert en Riesz & Sz.-Nagy (1990). Una explicación más sofisticada en el lenguaje de las álgebras C* se encuentra en Rudin (1973) o Kadison y Ringrose (1997).
106. Véase, por ejemplo, Riesz & Sz.-Nagy (1990, Capítulo VI) o Weidmann 1980, Capítulo 7. Schmidt (1908) ya conocía este resultado en el caso de operadores que surgen de núcleos integrales.
107. Riesz y Sz.-Nagy 1990, §§107-108
108. Shubin 1987
109. Rudin 1973, Teorema 13.30.
110. Thomas, Pynchon (1973). El arco iris de la gravedad . Prensa vikinga. págs.217, 275. ISBN 978-0143039945.

Referencias

• Axler, Sheldon (18 de diciembre de 2014), Álgebra lineal bien hecha , Textos universitarios en matemáticas (3.ª ed.), Springer Publishing (publicado en 2015), pág. 296, ISBN 978-3-319-11079-0
• Bachman, George; Narici, Lorenzo; Beckenstein, Edward (2000), Análisis de Fourier y wavelets , Universitext, Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-98899-3, señor  1729490.
• Bers, Lipman ; Juan, Fritz ; Schechter, Martin (1981), Ecuaciones diferenciales parciales , Sociedad Matemática Estadounidense, ISBN 978-0-8218-0049-2.
• Billingsley, Patrick (1986), Probabilidad y medida , Wiley.
• Bourbaki, Nicolas (1986), Teorías espectrales , Elementos de las matemáticas, Berlín: Springer-Verlag, ISBN 978-0-201-00767-1.
• Bourbaki, Nicolas (1987), Espacios vectoriales topológicos , Elementos de las matemáticas, Berlín: Springer-Verlag, ISBN 978-3-540-13627-9.
• Boyer, Carl Benjamín ; Merzbach, Uta C (1991), Una historia de las matemáticas (2ª ed.), John Wiley & Sons, Inc., ISBN 978-0-471-54397-8.
• Brenner, S.; Scott, RL (2005), La teoría matemática de los métodos de elementos finitos (2ª ed.), Springer, ISBN 978-0-387-95451-6.
• Brezis, Haim (2010), Análisis funcional, espacios de Sobolev y ecuaciones diferenciales parciales , Springer.
• Buttazzo, Giuseppe; Giaquinta, Mariano; Hildebrandt, Stefan (1998), Problemas variacionales unidimensionales , Serie de conferencias de Oxford sobre matemáticas y sus aplicaciones, vol. 15, The Clarendon Press Prensa de la Universidad de Oxford, ISBN 978-0-19-850465-8, señor  1694383.
• Clarkson, JA (1936), "Espacios uniformemente convexos", Trans. América. Matemáticas. Soc. , 40 (3): 396–414, doi : 10.2307/1989630 , JSTOR  1989630.
• Courant, Ricardo ; Hilbert, David (1953), Métodos de física matemática, vol. Yo , interciencia.
• Dieudonné, Jean (1960), Fundamentos del análisis moderno , Academic Press.
• Dirac, PAM (1930), Los principios de la mecánica cuántica , Oxford: Clarendon Press.
• Dunford, N.; Schwartz, JT (1958), Operadores lineales, Partes I y II , Wiley-Interscience.
• Duren, P. (1970), Teoría de los espacios H ^p , Nueva York: Academic Press.
• Einsiedler, Manfred; Ward, Thomas (2011), Teoría ergódica con miras a la teoría de números , Springer.
• Evans, LC (1998), Ecuaciones diferenciales parciales , Providence: Sociedad Matemática Estadounidense, ISBN 0-8218-0772-2.
• Folland, Gerald B. (2009), Análisis de Fourier y su aplicación (Reimpresión de Wadsworth y Brooks/Cole 1992 ed.), Librería de la American Mathematical Society, ISBN 978-0-8218-4790-9.
• Folland, Gerald B. (1989), Análisis armónico en el espacio de fases , Annals of Mathematics Studies, vol. 122, Prensa de la Universidad de Princeton, ISBN 978-0-691-08527-2.
• Fréchet, Maurice (1907), "Sur les ensembles de fonctions et les opérations linéaires", CR Acad. Ciencia. París , 144 : 1414-1416.
• Fréchet, Maurice (1904), "Sur les opérations linéaires", Transacciones de la Sociedad Matemática Estadounidense , 5 (4): 493–499, doi :10.2307/1986278, JSTOR  1986278.
• Giusti, Enrico (2003), Métodos directos en el cálculo de variaciones , World Scientific, ISBN 978-981-238-043-2.
• Grattan-Guinness, Ivor (2000), La búsqueda de raíces matemáticas, 1870-1940 , Libros en rústica de Princeton, Princeton University Press , ISBN 978-0-691-05858-0, señor  1807717.
• Halmos, Paul (1957), Introducción al espacio de Hilbert y la teoría de la multiplicidad espectral , Chelsea Pub. Co
• Halmos, Paul (1982), Un libro de problemas espaciales de Hilbert , Springer-Verlag, ISBN 978-0-387-90685-0.
• Hewitt, Edwin; Stromberg, Karl (1965), Análisis real y abstracto , Nueva York: Springer-Verlag.
• Hilbert, David ; Nordheim, Lothar Wolfgang ; von Neumann, John (1927), "Über die Grundlagen der Quantenmechanik", Mathematische Annalen , 98 : 1–30, doi :10.1007/BF01451579, S2CID  120986758.
• Holevo, Alexander S. (2001), Estructura estadística de la teoría cuántica , Apuntes de conferencias de física, Springer, ISBN 3-540-42082-7, OCLC  318268606.
• Kac, Mark (1966), "¿Se puede oír la forma de un tambor?", American Mathematical Monthly , 73 (4, parte 2): 1–23, doi :10.2307/2313748, JSTOR  2313748.
• Kadison, Richard V.; Ringrose, John R. (1997), Fundamentos de la teoría de álgebras de operadores. vol. I , Estudios de Posgrado en Matemáticas, vol. 15, Providence, RI: Sociedad Matemática Estadounidense , ISBN 978-0-8218-0819-1, señor  1468229.
• Kadison, Richard V.; Ringrose, John R. (1983), Fundamentos de la teoría de álgebras de operadores, vol. I: Teoría elemental , Nueva York: Academic Press, Inc.
• Karatzas, Ioannis; Shreve, Steven (2019), Movimiento browniano y cálculo estocástico (2ª ed.), Springer, ISBN 978-0-387-97655-6

• Kakutani, Shizuo (1939), "Algunas caracterizaciones del espacio euclidiano", Japanese Journal of Mathematics , 16 : 93–97, doi : 10.4099/jjm1924.16.0_93 , MR  0000895.
• Kline, Morris (1972), Pensamiento matemático desde la antigüedad hasta los tiempos modernos, Volumen 3 (3.ª ed.), Oxford University Press (publicado en 1990), ISBN 978-0-19-506137-6.
• Kolmogorov, Andrei ; Fomin, Sergei V. (1970), Introductory Real Analysis (edición revisada en inglés, traducción de Richard A. Silverman (1975) ed.), Dover Press, ISBN 978-0-486-61226-3.
• Krantz, Steven G. (2002), Teoría de funciones de varias variables complejas , Providence, RI: Sociedad Matemática Estadounidense , ISBN 978-0-8218-2724-6.
• Lanczos, Cornelius (1988), Análisis aplicado (reimpresión de 1956 Prentice-Hall ed.), Dover Publications, ISBN 978-0-486-65656-4.
• Lebesgue, Henri (1904), Leçons sur l'intégration et la recherche des fonctions primitives, Gauthier-Villars.
• Levitan, BM (2001) [1994], "Espacio de Hilbert", Enciclopedia de Matemáticas , EMS Press.
• Lindenstrauss, J.; Tzafriri, L. (1971), "Sobre el problema de los subespacios complementados", Israel Journal of Mathematics , 9 (2): 263–269, doi :10.1007/BF02771592, ISSN  0021-2172, MR  0276734, S2CID  119575718.
• Marsden, Jerrold E. (1974), Análisis clásico elemental , WH Freeman and Co., MR  0357693.
• Murphy, Gerald J. (1990), C* -álgebras y teoría del operador , Academic Press, ISBN 0-12-511360-9.
• von Neumann, John (1929), "Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren", Mathematische Annalen , 102 : 49–131, doi :10.1007/BF01782338, S2CID  121249803.
• von Neumann, John (1932), "Aplicaciones físicas de la hipótesis ergódica", Proc Natl Acad Sci USA , 18 (3): 263–266, Bibcode :1932PNAS...18..263N, doi : 10.1073/pnas.18.3 .263 , JSTOR  86260, PMC  1076204 , PMID  16587674.
• von Neumann, John (1955), Fundamentos matemáticos de la mecánica cuántica , Princeton Landmarks in Mathematics, traducido por Beyer, Robert T., Princeton University Press (publicado en 1996), ISBN 978-0-691-02893-4, señor  1435976.
• Nielsen, Michael A .; Chuang, Isaac L. (2000), Computación cuántica e información cuántica (1ª ed.), Cambridge: Cambridge University Press , ISBN 978-0-521-63503-5, OCLC  634735192.
• O'Connor, John J.; Robertson, Edmund F. (1996), "Espacios lineales abstractos", Archivo MacTutor de Historia de las Matemáticas , Universidad de St Andrews
• Pathria, RK (1996), Mecánica estadística (2 ed.), Academic Press.
• Pedersen, Gert (1995), Analysis Now , Textos de posgrado en matemáticas, vol. 118, Berlín, Nueva York: Springer-Verlag , ISBN 978-1-4612-6981-6, señor  0971256
• Peres, Asher (1993), Teoría cuántica: conceptos y métodos , Kluwer, ISBN 0-7923-2549-4, OCLC  28854083
• Prugovečki, Eduard (1981), Mecánica cuántica en el espacio de Hilbert (2ª ed.), Dover (publicado en 2006), ISBN 978-0-486-45327-9.
• Caña, Michael ; Simon, Barry (1980), Análisis funcional (vol I de 4 volúmenes) , Métodos de física matemática moderna, Academic Press, ISBN 978-0-12-585050-6.
• Caña, Michael ; Simon, Barry (1975), Análisis de Fourier, autoadjunción (vol II de 4 vols) , Métodos de física matemática moderna, Academic Press, ISBN 9780125850025.
• Rieffel, Eleanor G .; Polak, Wolfgang H. (4 de marzo de 2011), Computación cuántica: una suave introducción , MIT Press, ISBN 978-0-262-01506-6.
• Riesz, Frigyes (1907), "Sur une espèce de Géométrie analytique des systèmes de fonctions sommables", CR Acad. Ciencia. París , 144 : 1409-1411.
• Riesz, Frigyes (1934), "Zur Theorie des Hilbertschen Raumes", Acta Sci. Matemáticas. Szeged , 7 : 34–38.
• Riesz, Frigyes ; Sz.-Nagy, Béla (1990), Análisis funcional , Dover, ISBN 978-0-486-66289-3.
• Roman, Stephen (2008), Álgebra lineal avanzada , Textos de posgrado en matemáticas (tercera ed.), Springer, ISBN 978-0-387-72828-5
• Rudin, Walter (1973). Análisis funcional . Serie Internacional en Matemática Pura y Aplicada. vol. 25 (Primera ed.). Nueva York, NY: McGraw-Hill Ciencias/Ingeniería/Matemáticas . ISBN 9780070542259.
• Rudin, Walter (1987), Análisis real y complejo , McGraw-Hill, ISBN 978-0-07-100276-9.
• Saks, Stanisław (2005), Teoría de la integral (2ª ed. de Dover), Dover, ISBN 978-0-486-44648-6; Monografje Matematyczne , publicado originalmente , vol. 7, Varsovia, 1937.
• Schaefer, Helmut H .; Wolff, Manfred P. (1999). Espacios vectoriales topológicos . GTM . vol. 8 (Segunda ed.). Nueva York, NY: Springer Nueva York Pie de imprenta Springer. ISBN 978-1-4612-7155-0. OCLC  840278135.
• Schmidt, Erhard (1908), "Über die Auflösung linearer Gleichungen mit unendlich vielen Unbekannten", Rend. Circo. Estera. Palermo , 25 : 63–77, doi : 10.1007/BF03029116, S2CID  120666844.
• Shubin, MA (1987), Operadores pseudodiferenciales y teoría espectral , Springer Series in Soviet Mathematics, Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-13621-7, señor  0883081.
• Sobrino, Luis (1996), Elementos de la mecánica cuántica no relativista , River Edge, Nueva Jersey: World Scientific Publishing Co. Inc., Bibcode :1996lnrq.book.....S, doi :10.1142/2865, ISBN 978-981-02-2386-1, señor  1626401.
• Stapleton, James (1995), Modelos estadísticos lineales , John Wiley and Sons.
• Stewart, James (2006), Cálculo: conceptos y contextos (3ª ed.), Thomson/Brooks/Cole.
• Stein, E (1970), Integrales singulares y propiedades de diferenciabilidad de funciones , Universidad de Princeton. Prensa, ISBN 978-0-691-08079-6.
• Stein, Elías ; Weiss, Guido (1971), Introducción al análisis de Fourier en espacios euclidianos , Princeton, Nueva Jersey: Princeton University Press, ISBN 978-0-691-08078-9.
• Stein, E; Shakarchi, R (2005), Análisis real, teoría de la medida, integración y espacios de Hilbert , Princeton University Press.
• Streater, Ray ; Wightman, Arthur (1964), PCT, Spin and Statistics y todo eso , WA Benjamin, Inc.
• Stroock, Daniel (2011), Teoría de la probabilidad: una visión analítica (2 ed.), Cambridge University Press.
• Teschl, Gerald (2009). Métodos Matemáticos en Mecánica Cuántica; Con aplicaciones para operadores de Schrödinger. Providencia : Sociedad Matemática Estadounidense . ISBN 978-0-8218-4660-5..
• Titchmarsh, Edward Charles (1946), Expansiones de funciones propias, parte 1 , Universidad de Oxford: Clarendon Press.
• Trèves, François (1967), Espacios vectoriales topológicos, distribuciones y núcleos , Academic Press.
• Warner, Frank (1983), Fundamentos de variedades diferenciables y grupos de mentiras , Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-90894-6.
• Weidmann, Joachim (1980), Operadores lineales en espacios de Hilbert , Textos de Graduado en Matemáticas, vol. 68, Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-90427-6, señor  0566954.
• Weyl, Hermann (1931), La teoría de los grupos y la mecánica cuántica (edición en inglés de 1950), Dover Press, ISBN 978-0-486-60269-1.
• Young, Nicholas (1988), Introducción al espacio de Hilbert , Cambridge University Press, ISBN 978-0-521-33071-8, Zbl  0645.46024.

enlaces externos

• "Espacio de Hilbert", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Espacio de Hilbert en Mathworld
• 245B, notas 5: espacios de Hilbert por Terence Tao