Billar dinámico

El sistema dinámico abstrae un juego de billar ideal, con colisiones elásticas fuera de los límites.

Una partícula se mueve dentro del estadio Bunimovich, un conocido billar caótico. Consulte la sección Software para realizar dicha animación.

Un billar dinámico es un sistema dinámico en el que una partícula alterna entre movimiento libre (normalmente como línea recta) y reflexiones especulares de un límite. Cuando la partícula golpea el límite, se refleja sin pérdida de velocidad (es decir, colisiones elásticas). Los billares son idealizaciones hamiltonianas del juego de billar , pero donde la región contenida por el límite puede tener formas distintas a la rectangular e incluso ser multidimensional. El billar dinámico también puede estudiarse en geometrías no euclidianas ; de hecho, los primeros estudios del billar establecieron su movimiento ergódico sobre superficies de curvatura negativa constante . El estudio de los billares que se mantienen fuera de una región, en lugar de mantenerse en una región, se conoce como teoría del billar exterior .

El movimiento de la partícula en el billar es una línea recta, con energía constante, entre reflexiones con el límite (una geodésica si la métrica de Riemann de la mesa de billar no es plana). Todas las reflexiones son especulares : el ángulo de incidencia justo antes de la colisión es igual al ángulo de reflexión justo después de la colisión. La secuencia de reflexiones se describe mediante el mapa de billar que caracteriza completamente el movimiento de la partícula.

El billar captura toda la complejidad de los sistemas hamiltonianos, desde la integrabilidad hasta el movimiento caótico , sin las dificultades de integrar las ecuaciones de movimiento para determinar su mapa de Poincaré . Birkhoff demostró que un sistema de billar con mesa elíptica es integrable.

Ecuaciones de movimiento

El hamiltoniano para una partícula de masa m que se mueve libremente sin fricción sobre una superficie es:

${\displaystyle H(p,q)={\frac {p^{2}}{2m}}+V(q)}$

donde hay un potencial diseñado para ser cero dentro de la región en la que la partícula puede moverse, y infinito en caso contrario: ${\displaystyle V(q)}$ ${\displaystyle \Omega }$

${\displaystyle V(q)={\begin{cases}0&q\in \Omega \\\infty &q\notin \Omega \end{cases}}}$

Esta forma del potencial garantiza una reflexión especular en la frontera. El término cinético garantiza que la partícula se mueve en línea recta, sin ningún cambio de energía. Si la partícula se va a mover en una variedad no euclidiana , entonces la hamiltoniana se reemplaza por:

${\displaystyle H(p,q)={\frac {1}{2m}}p^{i}p^{j}g_{ij}(q)+V(q)}$

¿Dónde está el tensor métrico en el punto ? Debido a la estructura muy simple de este hamiltoniano, las ecuaciones de movimiento de la partícula, las ecuaciones de Hamilton-Jacobi , no son más que las ecuaciones geodésicas de la variedad: la partícula se mueve a lo largo de geodésicas . ${\displaystyle g_{ij}(q)}$ ${\displaystyle q\;\in \;\Omega }$

Billar notable y clases de billar.

El billar de Hadamard

El billar de Hadamard se refiere al movimiento de una partícula puntual libre sobre una superficie de curvatura negativa constante, en particular, la superficie compacta de Riemann más simple con curvatura negativa, una superficie del género 2 (un donut de dos agujeros). El modelo tiene solución exacta y viene dado por el flujo geodésico en la superficie. Es el ejemplo más antiguo de caos determinista jamás estudiado, ya que fue introducido por Jacques Hadamard en 1898.

El billar de Artin.

El billar de Artin considera el movimiento libre de una partícula puntual sobre una superficie de curvatura negativa constante, en particular, la superficie de Riemann no compacta más simple , una superficie con una cúspide. Se destaca por ser exactamente solucionable y, sin embargo, no solo ergódico sino también fuertemente mezclable . Es un ejemplo de sistema Anosov . Este sistema fue estudiado por primera vez por Emil Artin en 1924.

Billar dispersivo y semidispersante.

Sea M una variedad Riemanniana suave y completa sin límite, cuya curvatura seccional máxima no es mayor que K y con un radio de inyectividad . Considere una colección de n subconjuntos (paredes) geodésicamente convexos , tal que sus límites sean subvariedades suaves de codimensión uno. Sea , donde denota el interior del conjunto . El conjunto se llamará mesa de billar. Consideremos ahora una partícula que se mueve dentro del conjunto B con velocidad unitaria a lo largo de una geodésica hasta llegar a uno de los conjuntos B _i (tal evento se llama colisión) donde se refleja de acuerdo con la ley “el ángulo de incidencia es igual al ángulo de reflexión” (si llega a uno de los conjuntos , , la trayectoria no queda definida a partir de ese momento). Este sistema dinámico se denomina billar semidispersante . Si las paredes son estrictamente convexas, entonces el billar se llama dispersivo . La denominación está motivada por la observación de que un haz de trayectorias localmente paralelo se dispersa después de una colisión con una parte estrictamente convexa de una pared, pero permanece localmente paralelo después de una colisión con una sección plana de una pared. ${\displaystyle \rho >0}$ ${\displaystyle B_{i}\subset M}$ ${\displaystyle i=1,\ldots ,n}$ ${\displaystyle B=M\ (\bigcup _{i=1}^{n}\operatorname {Int} (B_{i}))}$ ${\displaystyle \operatorname {Int} (B_{i})}$ ${\displaystyle B_{i}}$ ${\displaystyle B\subset M}$ ${\displaystyle B_{i}\cap B_{j}}$ ${\displaystyle i\neq j}$

El límite de dispersión juega el mismo papel en el billar que la curvatura negativa en los flujos geodésicos, lo que provoca la inestabilidad exponencial de la dinámica. Es precisamente este mecanismo de dispersión el que confiere al billar de dispersión sus propiedades caóticas más fuertes , como lo estableció Yakov G. Sinai . ^[1] Es decir, los billares son ergódicos , mixtos , Bernoulli , que tienen una entropía Kolmogorov-Sinai positiva y una decadencia exponencial de correlaciones .

Las propiedades caóticas de los billares semidispersantes generales no se comprenden tan bien; sin embargo, las de un tipo importante de billar semidispersivo, el gas de bola dura, se estudiaron con cierto detalle desde 1975 (consulte la siguiente sección).

Los resultados generales de Dmitri Burago y Serge Ferleger ^[2] sobre la estimación uniforme del número de colisiones en billares semidispersos no degenerados permiten establecer la finitud de su entropía topológica y no más que el crecimiento exponencial de las trayectorias periódicas. ^[3] Por el contrario, los billares semidispersos degenerados pueden tener una entropía topológica infinita. ^[4]

Gas Lorentz, también conocido como billar del Sinaí

Una partícula que se mueve dentro del billar del Sinaí, también conocida como gas de Lorentz.

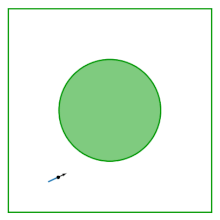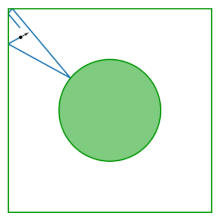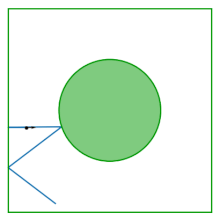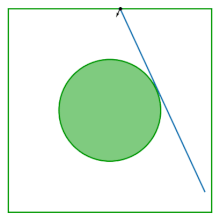
La mesa del gas de Lorentz (también conocida como billar del Sinaí) es un cuadrado al que se le retira un disco de su centro; la mesa es plana y no tiene curvatura. El billar surge del estudio del comportamiento de dos discos que interactúan y rebotan dentro de un cuadrado, reflejándose en los límites del cuadrado y entre sí. Al eliminar el centro de masa como variable de configuración, la dinámica de dos discos que interactúan se reduce a la dinámica del billar del Sinaí.

El billar fue introducido por Yakov G. Sinai como un ejemplo de un sistema hamiltoniano interactivo que muestra propiedades físicas termodinámicas: casi todas (hasta una medida cero) de sus posibles trayectorias son ergódicas y tiene un exponente de Lyapunov positivo .

El gran logro del Sinaí con este modelo fue demostrar que el conjunto clásico de Boltzmann-Gibbs para un gas ideal es esencialmente el billar de Hadamard máximamente caótico.

Billar bola que rebota

Una partícula está sometida a una fuerza constante (por ejemplo, la gravedad de la Tierra) y se dispersa de forma inelástica sobre un suelo que vibra periódicamente. Cuando el suelo está formado por arcos o círculos, en un determinado intervalo de frecuencias, se pueden dar estimaciones semianalíticas de la tasa de separación exponencial de las trayectorias. ^[5]

estadio Bunimovich

La mesa llamada estadio Bunimovich es un rectángulo coronado por semicírculos, una forma llamada estadio . Hasta que fue introducido por Leonid Bunimovich , se pensaba que los billares con exponentes positivos de Lyapunov necesitaban dispersiones convexas, como el disco del billar del Sinaí, para producir la divergencia exponencial de las órbitas. Bunimovich demostró que al considerar las órbitas más allá del punto de enfoque de una región cóncava era posible obtener una divergencia exponencial.

billar magnético

Movimiento de una partícula cargada dentro de un billar del Sinaí con campo magnético perpendicular.

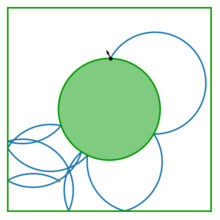
El billar magnético representa un billar en el que una partícula cargada se propaga en presencia de un campo magnético perpendicular. Como resultado, la trayectoria de la partícula cambia de una línea recta a un arco de círculo. El radio de este círculo es inversamente proporcional a la intensidad del campo magnético. Estos billares han sido útiles en aplicaciones del billar en el mundo real, normalmente modelando nanodispositivos (ver Aplicaciones).

Billar generalizado

El billar generalizado (GB) describe el movimiento de un punto de masa (una partícula) dentro de un dominio cerrado con un límite suave por partes . En la frontera, la velocidad del punto se transforma cuando la partícula sufre la acción de la ley del billar generalizada. GB fueron introducidos por Lev D. Pustyl'nikov en el caso general ^[6] y, en el caso en que se trata de un paralelepípedo ^[7] en relación con la justificación de la segunda ley de la termodinámica . Desde el punto de vista físico, GB describe un gas formado por un número finito de partículas que se mueven en un recipiente, mientras las paredes del recipiente se calientan o enfrían. La esencia de la generalización es la siguiente. Cuando la partícula golpea la frontera , su velocidad se transforma con la ayuda de una función dada , definida sobre el producto directo (donde está la línea real, es un punto de la frontera y es el tiempo), de acuerdo con la siguiente ley. Supongamos que la trayectoria de la partícula, que se mueve con la velocidad , se cruza en el punto en el tiempo . Luego, en un momento dado, la partícula adquiere la velocidad , como si sufriera un empuje elástico desde el plano infinitamente pesado , que es tangente a en el punto , y en un momento se mueve a lo largo de la normal a en con la velocidad . Destacamos que la posición del límite en sí es fija, mientras que su acción sobre la partícula se define a través de la función . ${\displaystyle \Pi \,\subset \,\mathbb {R} ^{n}}$ ${\displaystyle \Gamma }$ ${\displaystyle \Gamma }$ ${\displaystyle \Pi }$ ${\displaystyle \Gamma }$ ${\displaystyle f(\gamma ,\,t)}$ ${\displaystyle \Gamma \,\times \,\mathbb {R} ^{1}}$ ${\displaystyle \mathbb {R} ^{1}}$ ${\displaystyle \gamma \,\in \,\Gamma }$ ${\displaystyle t\,\in \,\mathbb {R} ^{1}}$ ${\displaystyle v}$ ${\displaystyle \Gamma }$ ${\displaystyle \gamma \,\in \,\Gamma }$ ${\displaystyle t^{*}}$ ${\displaystyle t^{*}}$ ${\displaystyle v^{*}}$ ${\displaystyle \Gamma ^{*}}$ ${\displaystyle \Gamma }$ ${\displaystyle \gamma }$ ${\displaystyle t^{*}}$ ${\displaystyle \Gamma }$ ${\displaystyle \gamma }$ ${\displaystyle \textstyle {\frac {\partial f}{\partial t}}(\gamma ,\,t^{*})}$ ${\displaystyle f}$

Consideramos que la dirección positiva del movimiento del avión es hacia el interior de . Por tanto, si la derivada es , entonces la partícula se acelera después del impacto. ${\displaystyle \Gamma ^{*}}$ ${\displaystyle \Pi }$ ${\displaystyle \textstyle {\frac {\partial f}{\partial t}}(\gamma ,\,t)\;>\;0}$

Si la velocidad adquirida por la partícula como resultado de la ley de reflexión anterior se dirige al interior del dominio , entonces la partícula abandonará el límite y continuará moviéndose hasta la próxima colisión con . Si la velocidad se dirige hacia el exterior de , entonces la partícula permanece en el punto hasta que en algún momento la interacción con el límite la obligará a abandonarlo. ${\displaystyle v^{*}}$ ${\displaystyle \Pi }$ ${\displaystyle \Pi }$ ${\displaystyle \Gamma }$ ${\displaystyle v^{*}}$ ${\displaystyle \Pi }$ ${\displaystyle \Gamma }$ ${\displaystyle \gamma }$ ${\displaystyle {\tilde {t}}\;>\;t^{*}}$

Si la función no depende del tiempo ; es decir , el billar generalizado coincide con el clásico. ${\displaystyle f(\gamma ,\,t)}$ ${\displaystyle t}$ ${\displaystyle \textstyle {\frac {\partial f}{\partial t}}\;=\;0}$

Esta ley de reflexión generalizada es muy natural. En primer lugar, refleja un hecho obvio de que las paredes del recipiente con gas están inmóviles. En segundo lugar, la acción de la pared sobre la partícula sigue siendo el clásico empuje elástico. En esencia, consideramos fronteras que se mueven infinitamente con velocidades dadas.

Se considera la reflexión desde la frontera tanto en el marco de la mecánica clásica (caso newtoniano) como de la teoría de la relatividad (caso relativista). ${\displaystyle \Gamma }$

Resultados principales: en el caso newtoniano la energía de la partícula está limitada, la entropía de Gibbs es una constante, ^{[7] [8] [9]} (en Notas) y en el caso relativista la energía de la partícula, la entropía de Gibbs, la entropía con con respecto al volumen de fase crece hasta el infinito, ^{[7] [9]} (en Notas), referencias al billar generalizado.

Caos cuántico

La versión cuántica del billar se estudia fácilmente de varias maneras. El hamiltoniano clásico para el billar, dado anteriormente, se reemplaza por la ecuación de Schrödinger en estado estacionario o, más precisamente, ${\displaystyle H\psi \;=\;E\psi }$

${\displaystyle -{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\psi _{n}(q)=E_{n}\psi _{n}(q)}$

¿Dónde está el laplaciano ? El potencial que es infinito fuera de la región pero cero dentro de ella se traduce en las condiciones de frontera de Dirichlet : ${\displaystyle \nabla ^{2}}$ ${\displaystyle \Omega }$

${\displaystyle \psi _{n}(q)=0\quad {\mbox{for}}\quad q\notin \Omega }$

Como es habitual, las funciones de onda se consideran ortonormales :

${\displaystyle \int _{\Omega }{\overline {\psi _{m}}}(q)\psi _{n}(q)\,dq=\delta _{mn}}$

Curiosamente, la ecuación de Schrödinger en campo libre es la misma que la ecuación de Helmholtz ,

${\displaystyle \left(\nabla ^{2}+k^{2}\right)\psi =0}$

con

${\displaystyle k^{2}={\frac {1}{\hbar ^{2}}}2mE_{n}}$

Esto implica que los billares cuánticos bidimensionales y tridimensionales pueden modelarse mediante los modos de resonancia clásicos de una cavidad de radar de una forma determinada, abriendo así una puerta a la verificación experimental. (El estudio de los modos de la cavidad del radar debe limitarse a los modos magnéticos transversales (TM), ya que estos son los que obedecen a las condiciones de contorno de Dirichlet).

El límite semiclásico corresponde al que puede verse equivalente a , aumentando la masa para que se comporte clásicamente. ${\displaystyle \hbar \;\to \;0}$ ${\displaystyle m\;\to \;\infty }$

Como afirmación general, se puede decir que siempre que las ecuaciones clásicas de movimiento sean integrables (por ejemplo, mesas de billar rectangulares o circulares), entonces la versión mecánico-cuántica de los billares es completamente solucionable. Cuando el sistema clásico es caótico, entonces el sistema cuántico generalmente no tiene solución exacta y presenta numerosas dificultades en su cuantificación y evaluación. El estudio general de los sistemas cuánticos caóticos se conoce como caos cuántico .

Un ejemplo particularmente sorprendente de cicatrización en una mesa elíptica lo da la observación del llamado espejismo cuántico .

Aplicaciones

El billar, tanto cuántico como clásico, se ha aplicado en varias áreas de la física para modelar sistemas del mundo real bastante diversos. Los ejemplos incluyen rayos ópticos , ^[10] láseres , ^{[11] [12]} acústica , ^[13] fibras ópticas (por ejemplo, fibras de doble revestimiento ^{[14] [15]} ) o correspondencia cuántica clásica. ^[16] Una de sus aplicaciones más frecuentes es modelar partículas que se mueven dentro de nanodispositivos, por ejemplo puntos cuánticos , ^{[17] [18]} uniones pn , ^[19] superredes antídoto, ^{[20] [21]} entre otros. La razón de esta eficacia ampliamente difundida del billar como modelo físico reside en el hecho de que en situaciones con una pequeña cantidad de desorden o ruido, el movimiento de, por ejemplo, partículas como los electrones o los rayos de luz, es muy similar al movimiento del punto. partículas en el billar. Además, la naturaleza conservadora de energía de las colisiones de partículas es un reflejo directo de la conservación de energía de la mecánica hamiltoniana.

Software

Existe software de código abierto para simular billar para varios lenguajes de programación. Del más reciente al más antiguo, el software existente es: DynamicalBilliards.jl (Julia), Bill2D (C++) y Billiard Simulator (Matlab). Las animaciones presentes en esta página se realizaron con DynamicalBilliards.jl.

Ver también

• Modelo Fermi-Ulam (billar con paredes oscilantes )
• El algoritmo de compresión de Lubachevsky-Stillinger simula esferas duras que chocan no solo con los límites sino también entre sí mientras crecen en tamaño ^[15]
• billar aritmético
• Problema de iluminación

Notas

1. "Copia archivada" (PDF) . Archivado desde el original (PDF) el 31 de diciembre de 2013 . Consultado el 6 de junio de 2014 .{{cite web}}: Mantenimiento CS1: copia archivada como título ( enlace )
2. Burago, D.; Ferleger, S.; Kononenko, A. (1 de enero de 1998). "Estimaciones uniformes sobre el número de colisiones en billares semidispersos". Anales de Matemáticas . 147 (3): 695–708. doi :10.2307/120962. JSTOR  120962.
3. Burago, D.; Ferleger, S. (26 de mayo de 1997). "Entropía topológica del billar semidispersante". Teoría ergódica y sistemas dinámicos . 18 (4): 791. doi :10.1017/S0143385798108246. S2CID  122549772.
4. Burago, D. (1 de febrero de 2006). "Billar semidispersante de entropía topológica infinita". Teoría ergódica y sistemas dinámicos . 26 (1): 45–52. doi :10.1017/S0143385704001002. S2CID  121644309.
5. Mátyás, László; Barna, Imre Ferenc (2011). "Origen geométrico del caos en el billar de bolas que rebotan". Caos, solitones y fractales . 44 (12): 1111-1116. arXiv : 1003.2505 . doi :10.1016/j.caos.2011.10.002.
6. Pustyl'nikov, LD (1999). "La ley del aumento de entropía y el billar generalizado". Encuestas matemáticas rusas . 54 (3): 650–651. Código Bib : 1999RuMaS..54..650P. doi :10.1070/rm1999v054n03abeh000168. S2CID  250902640.
7. Pustyl'nikov, LD (1995). "Modelos de Poincaré, justificación rigurosa de la segunda ley de la termodinámica desde la mecánica y el mecanismo de aceleración de Fermi". Encuestas matemáticas rusas . 50 (1): 145–189. Código Bib : 1995RuMaS..50..145P. doi :10.1070/rm1995v050n01abeh001663. S2CID  250875392.
8. Pustyl'nikov, LD (2005). "Billar periódico newtoniano generalizado en una bola". Encuestas matemáticas rusas . 60 (2): 365–366. Código Bib : 2005RuMaS..60..365P. doi :10.1070/RM2005v060n02ABEH000839. S2CID  250856558.
9. Deryabin, Mikhail V.; Pustyl'nikov, Lev D. (2007). "Gas de desequilibrio y billar generalizado". Revista de Física Estadística . 126 (1): 117-132. Código Bib : 2007JSP...126..117D. doi :10.1007/s10955-006-9250-4. S2CID  55957240.
10. Kouznetsov, Dmitrii; Moloney, Jerome V. (septiembre de 2004). "Comportamiento límite de modos de un Dirichlet Laplaciano". Revista de Óptica Moderna . 51 (13): 1955-1962. Código Bib : 2004JMOp...51.1955K. doi :10.1080/09500340408232504. ISSN  0950-0340. S2CID  30880255.
11. Stone, A. Douglas (junio de 2010). "Láseres de billar caóticos". Naturaleza . 465 (7299): 696–697. doi : 10.1038/465696a . ISSN  1476-4687. PMID  20535191.
12. Gmachl, C. (5 de junio de 1998). "Emisión direccional de alta potencia de microláseres con resonadores caóticos". Ciencia . 280 (5369): 1556-1564. arXiv : cond-mat/9806183 . Código Bib : 1998 Ciencia... 280.1556G. doi : 10.1126/ciencia.280.5369.1556. PMID  9616111. S2CID  502055.
13. Koyanagi, Sin'ichiro; Nakano, Takeru; Kawabe, Tetsuji (1 de agosto de 2008). "Aplicación del hamiltoniano del movimiento de rayos a la acústica de una habitación". La Revista de la Sociedad de Acústica de América . 124 (2): 719–722. Código Bib : 2008ASAJ..124..719K. doi : 10.1121/1.2946714. ISSN  0001-4966. PMID  18681564.
14. Leproux, P.; S. Fevrier; V. Doya; P. Roy; D. Pagnoux (2003). "Modelado y optimización de amplificadores de fibra de doble revestimiento mediante propagación caótica de bomba". Tecnología de Fibra Óptica . 7 (4): 324–339. Código Bib : 2001OptFT...7..324L. doi :10.1006/ofte.2001.0361.
15. BD Lubachevsky y FH Stillinger, Propiedades geométricas de empaquetamientos de discos aleatorios, J. Statistical Physics 60 (1990), 561-583 http://www.princeton.edu/~fhs/geodisk/geodisk.pdf
16. Stöckmann, H.-J.; Stein, J. (7 de mayo de 1990). " Caos cuántico en billar estudiado por absorción de microondas". Cartas de revisión física . 64 (19): 2215–2218. Código bibliográfico : 1990PhRvL..64.2215S. doi : 10.1103/PhysRevLett.64.2215. ISSN  0031-9007. PMID  10041617.
17. Ponomarenko, Luisiana; Schedin, F.; Katsnelson, Michigan; Yang, R.; Hill, EW; Novoselov, KS; Geim, Alaska (18 de abril de 2008). "Billar caótico Dirac en puntos cuánticos de grafeno". Ciencia . 320 (5874): 356–358. arXiv : 0801.0160 . Código Bib : 2008 Ciencia... 320.. 356P. doi : 10.1126/ciencia.1154663. ISSN  0036-8075. PMID  18420930. S2CID  206511356.
18. Pájaro, Jonathan P., ed. (2003). Transporte de electrones en puntos cuánticos . doi :10.1007/978-1-4615-0437-5. ISBN 978-1-4020-7459-2.
19. Chen, Shaowen; Han, Zheng; Elahi, Mirza M.; Habib, KM Masum; Wang, Lei; Wen, Bo; Gao, Yuanda; Taniguchi, Takashi; Watanabe, Kenji; Cariño, James; Ghosh, Avik W. (30 de septiembre de 2016). "Óptica electrónica con uniones pn en grafeno balístico". Ciencia . 353 (6307): 1522-1525. arXiv : 1602.08182 . Código Bib : 2016 Ciencia... 353.1522C. doi : 10.1126/ciencia.aaf5481. ISSN  0036-8075. PMID  27708099. S2CID  118443999.
20. Weiss, D.; Roukes, ML; Menschig, A.; Grambow, P.; von Klitzing, K.; Weimann, G. (27 de mayo de 1991). "Pinball de electrones y órbitas proporcionales en una serie periódica de dispersores" (PDF) . Cartas de revisión física . 66 (21): 2790–2793. Código bibliográfico : 1991PhRvL..66.2790W. doi : 10.1103/PhysRevLett.66.2790. ISSN  0031-9007. PMID  10043617.
21. Datseris, George; Geisel, Theo; Fleischmann, Ragnar (30 de abril de 2019). "Robustez del transporte balístico en superredes de antídoto". Nueva Revista de Física . 21 (4): 043051. arXiv : 1711.05833 . Código Bib : 2019NJPh...21d3051D. doi : 10.1088/1367-2630/ab19cc . ISSN  1367-2630.

Referencias

El billar del Sinaí

• Sinaí, Ya. G. (1963). "[Sobre los fundamentos de la hipótesis ergódica para un sistema dinámico de mecánica estadística]". Doklady Akademii Nauk SSSR (en ruso). 153 (6): 1261-1264.(en inglés, Sov. Math Dokl. 4 (1963) págs. 1818–1822).
• Sí. G. Sinai, "Sistemas dinámicos con reflejos elásticos", Russian Mathematical Surveys , 25 , (1970) págs.
• VI Arnold y A. Avez, Théorie ergodique des systèms dynamiques , (1967), Gauthier-Villars, París. (Edición en inglés: Benjamin-Cummings, Reading, Mass. 1968). (Proporciona debates y referencias sobre el billar del Sinaí).
• D. Heitmann, JP Kotthaus, "La espectroscopia de matrices de puntos cuánticos", Physics Today (1993), págs. (Proporciona una revisión de las pruebas experimentales de versiones cuánticas de los billares del Sinaí realizadas como estructuras a nanoescala (mesoscópicas) en obleas de silicio).
• S. Sridhar y WT Lu, "Sinai Billiards, Ruelle Zeta-functions and Ruelle Resonances: Microwave Experiments", (2002) Journal of Statistical Physics , vol. 108 Nos. 5/6, págs. 755–766.
• Linas Vepstas, Los billares del Sinaí , (2001). (Proporciona imágenes con trazado de rayos de los billares del Sinaí en un espacio tridimensional. Estas imágenes proporcionan una demostración gráfica e intuitiva de la fuerte ergodicidad del sistema).
• N. Chernov y R. Markarian, "Chaotic Billiards", 2006, Estudio matemático y monografías nº 127, AMS.

Billar extraño

• T. Schürmann e I. Hoffmann, La entropía de billares extraños dentro de n-simplex. J. Física. A28, página 5033 y siguientes, 1995. Documento PDF

estadio Bunimovich

• LABUnimovich (1979). "Sobre las propiedades ergódicas del billar que no se dispersa en ninguna parte". Física Matemáticas Comunitarias . 65 (3): 295–312. Código bibliográfico : 1979CMaPh..65..295B. doi :10.1007/BF01197884. S2CID  120456503.
• LABunimovich & Ya. G. Sinaí (1980). "Particiones de Markov para billar disperso". Física Matemáticas Comunitarias . 78 (2): 247–280. Código bibliográfico : 1980CMaPh..78..247B. doi :10.1007/bf01942372. S2CID  123383548.
• Animación flash que ilustra el caótico estadio Bunimovich.

Billar generalizado

• MV Deryabin y LD Pustyl'nikov, "Billar relativista generalizado", Reg. y Caótico Dyn. 8(3), págs. 283–296 (2003).
• MV Deryabin y LD Pustyl'nikov, "Sobre el billar relativista generalizado en campos de fuerza externos", Letters in Mathematical Physics , 63(3), págs. 195-207 (2003).
• MV Deryabin y LD Pustyl'nikov, "Atractores exponenciales en billar relativista generalizado", Comm. Matemáticas. Física. 248(3), págs. 527–552 (2004).

enlaces externos

• Weisstein, Eric W. "Billar". MundoMatemático .
• Entrada de Scholarpedia sobre billar dinámico (Leonid Bunimovich)
• Introducción a los sistemas dinámicos mediante billar, Instituto Max Planck de Física de Sistemas Complejos