Curvatura

Medida matemática de cuánto se desvía una curva o superficie de la planitud

Una célula migratoria de Dictyostelium discoideum de tipo salvaje cuyo límite está coloreado por la curvatura. Barra de escala: 5 µm.

En matemáticas , la curvatura es cualquiera de varios conceptos fuertemente relacionados en geometría que miden intuitivamente la cantidad en la que una curva se desvía de ser una línea recta o en la que una superficie se desvía de ser un plano . Si una curva o superficie está contenida en un espacio más grande, la curvatura se puede definir extrínsecamente en relación con el espacio ambiental. La curvatura de variedades de Riemann de dimensión al menos dos se puede definir intrínsecamente sin referencia a un espacio mayor.

Para las curvas, el ejemplo canónico es el de un círculo , que tiene una curvatura igual al recíproco de su radio . Los círculos más pequeños se doblan más pronunciadamente y, por tanto, tienen una curvatura mayor. La curvatura en un punto de una curva diferenciable es la curvatura de su círculo osculador , es decir el círculo que mejor se aproxima a la curva cerca de este punto. La curvatura de una recta es cero. A diferencia de la tangente , que es una cantidad vectorial, la curvatura en un punto suele ser una cantidad escalar , es decir, se expresa mediante un único número real .

Para superficies (y, más generalmente, para variedades de dimensiones superiores ), que están incrustadas en un espacio euclidiano , el concepto de curvatura es más complejo, ya que depende de la elección de una dirección en la superficie o variedad. Esto lleva a los conceptos de curvatura máxima , curvatura mínima y curvatura media .

Historia

En Tractatus de Configurationibus qualitatum et motuum, ^[1] la filósofa y matemática del siglo XIV Nicole Oresme introduce el concepto de curvatura como una medida de desviación de la rectitud; para círculos tiene la curvatura inversamente proporcional al radio; e intenta extender esta idea a otras curvas como una magnitud que varía continuamente. ^[2]

La curvatura de una curva diferenciable se definió originalmente mediante círculos osculadores . En este contexto, Augustin-Louis Cauchy demostró que el centro de curvatura es el punto de intersección de dos líneas normales infinitamente cercanas a la curva. ^[3]

Curvas planas

Intuitivamente, la curvatura describe para cualquier parte de una curva cuánto cambia la dirección de la curva en una pequeña distancia recorrida (por ejemplo, ángulo en rad/m ), por lo que es una medida de la tasa instantánea de cambio de dirección de un punto que se mueve. la curva: cuanto mayor es la curvatura, mayor es la tasa de cambio. En otras palabras, la curvatura mide qué tan rápido gira el vector unitario tangente a la curva ^[4] (rápido en términos de posición de la curva). De hecho, se puede demostrar que esta tasa de cambio instantánea es exactamente la curvatura. Más precisamente, supongamos que el punto se mueve sobre la curva a una velocidad constante de una unidad, es decir, la posición del punto P ( s ) es función del parámetro s , que puede pensarse como el tiempo o como el longitud del arco desde un origen dado. Sea T ( s ) un vector unitario tangente de la curva en P ( s ) , que también es la derivada de P ( s ) con respecto a s . Entonces, la derivada de T ( s ) respecto de s es un vector normal a la curva y cuya longitud es la curvatura.

Para que tenga sentido, la definición de la curvatura y sus diferentes caracterizaciones requieren que la curva sea continuamente diferenciable cerca de P , por tener una tangente que varía continuamente; requiere también que la curva sea dos veces diferenciable en P , para asegurar la existencia de los límites involucrados, y de la derivada de T ( s ) .

La caracterización de la curvatura en términos de la derivada del vector unitario tangente es probablemente menos intuitiva que la definición en términos del círculo osculador, pero las fórmulas para calcular la curvatura son más fáciles de deducir. Por ello, y también por su uso en cinemática , esta caracterización suele darse como definición de la curvatura.

círculo osculador

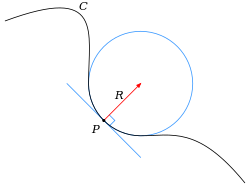
Históricamente, la curvatura de una curva diferenciable se definía a través del círculo osculador , que es el círculo que mejor se aproxima a la curva en un punto. Más precisamente, dado un punto P en una curva, cada dos puntos Q de la curva define un círculo (o a veces una línea) que pasa por Q y es tangente a la curva en P. El círculo osculador es el límite , si existe, de este círculo cuando Q tiende a P. Entonces el centro y el radio de curvatura de la curva en P son el centro y el radio del círculo osculador. La curvatura es el recíproco del radio de curvatura. Es decir, la curvatura es

${\displaystyle \kappa ={\frac {1}{R}},}$

donde R es el radio de curvatura ^[5] (todo el círculo tiene esta curvatura, se puede leer como un giro 2π sobre la longitud 2π R ).

Esta definición es difícil de manipular y expresar en fórmulas. Por tanto, se han introducido otras definiciones equivalentes.

En términos de parametrización de longitud de arco.

Cada curva diferenciable se puede parametrizar con respecto a la longitud del arco . ^[6] En el caso de una curva plana, esto significa la existencia de una parametrización γ ( s ) = ( x ( s ), y ( s )) , donde x e y son funciones diferenciables de valores reales cuyas derivadas satisfacen

${\displaystyle \|{\boldsymbol {\gamma }}'\|={\sqrt {x'(s)^{2}+y'(s)^{2}}}=1.}$

Esto significa que el vector tangente

${\displaystyle \mathbf {T} (s)={\bigl (}x'(s),y'(s){\bigr )}}$

tiene una longitud igual a uno y por tanto es un vector unitario tangente .

Si la curva es dos veces diferenciable, es decir, si existen las segundas derivadas de x e y , entonces existe la derivada de T ( s ) . Este vector es normal a la curva, su longitud es la curvatura κ ( s ) y está orientado hacia el centro de curvatura. Eso es,

${\displaystyle {\begin{aligned}\mathbf {T} (s)&={\boldsymbol {\gamma }}'(s),\\[8mu]\|\mathbf {T} (s)\|^{2}&=1\ {\text{(constant)}}\implies \mathbf {T} '(s)\cdot \mathbf {T} (s)=0,\\[5mu]\kappa (s)&=\|\mathbf {T} '(s)\|=\|{\boldsymbol {\gamma }}''(s)\|={\sqrt {x''(s)^{2}+y''(s)^{2}}}\end{aligned}}}$

Además, como el radio de curvatura es (asumiendo 𝜿 ( s ) ≠ 0)

${\displaystyle R(s)={\frac {1}{\kappa (s)}},}$

y el centro de curvatura está en la normal a la curva, el centro de curvatura es el punto

${\displaystyle \mathbf {C} (s)={\boldsymbol {\gamma }}(s)+{\frac {1}{\kappa (s)^{2}}}\mathbf {T} '(s).}$

(En caso de que la curvatura sea cero, el centro de curvatura no está ubicado en ningún lugar del plano R ² y a menudo se dice que está ubicado "en el infinito".)

Si N ( s ) es el vector normal unitario obtenido de T ( s ) mediante una rotación en sentido antihorario deπ/2, entonces

${\displaystyle \mathbf {T} '(s)=k(s)\mathbf {N} (s),}$

con k ( s ) = ± κ ( s ) . El número real k ( s ) se llama curvatura orientada o curvatura con signo . Depende tanto de la orientación del plano (definición de antihorario) como de la orientación de la curva proporcionada por la parametrización. De hecho, el cambio de variable s → – s proporciona otra parametrización de longitud de arco y cambia el signo de k ( s ) .

En términos de una parametrización general.

Sea γ ( t ) = ( x ( t ), y ( t )) una representación paramétrica adecuada de una curva plana dos veces diferenciable. Aquí propio significa que en el dominio de definición de la parametrización, la derivadare γ/dtestá definido, diferenciable y en ninguna parte igual al vector cero.

Con tal parametrización, la curvatura con signo es

${\displaystyle k={\frac {x'y''-y'x''}{{\bigl (}{x'}^{2}+{y'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}},}$

donde los primos se refieren a derivadas con respecto a t . La curvatura κ es por tanto

${\displaystyle \kappa ={\frac {\left|x'y''-y'x''\right|}{{\bigl (}{x'}^{2}+{y'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}}.}$

Estos se pueden expresar de forma libre de coordenadas como

${\displaystyle k={\frac {\det \left({\boldsymbol {\gamma }}',{\boldsymbol {\gamma }}''\right)}{\|{\boldsymbol {\gamma }}'\|^{3}}},\qquad \kappa ={\frac {\left|\det \left({\boldsymbol {\gamma }}',{\boldsymbol {\gamma }}''\right)\right|}{\|{\boldsymbol {\gamma }}'\|^{3}}}.}$

Estas fórmulas se pueden derivar del caso especial de parametrización de longitud de arco de la siguiente manera. La condición anterior sobre la parametrización implica que la longitud del arco s es una función monótona diferenciable del parámetro t y, a la inversa, que t es una función monótona de s . Además, al cambiar, si es necesario, s por – s , se puede suponer que estas funciones son crecientes y tienen una derivada positiva. Usando la notación de la sección anterior y la regla de la cadena , se tiene

${\displaystyle {\frac {d{\boldsymbol {\gamma }}}{dt}}={\frac {ds}{dt}}\mathbf {T} ,}$

y así, tomando la norma de ambos lados

${\displaystyle {\frac {dt}{ds}}={\frac {1}{\|{\boldsymbol {\gamma }}'\|}},}$

donde el primo denota diferenciación con respecto a t .

La curvatura es la norma de la derivada de T con respecto a s . Al utilizar la fórmula anterior y la regla de la cadena, esta derivada y su norma se pueden expresar en términos de γ ′ y γ ″ únicamente, con el parámetro de longitud de arco s completamente eliminado, dando las fórmulas anteriores para la curvatura.

Gráfica de una función

La gráfica de una función y = f ( x ) , es un caso especial de una curva parametrizada, de la forma

${\displaystyle {\begin{aligned}x&=t\\y&=f(t).\end{aligned}}}$

Como la primera y segunda derivada de x son 1 y 0, las fórmulas anteriores se simplifican a

${\displaystyle \kappa ={\frac {\left|y''\right|}{{\bigl (}1+{y'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}},}$

para la curvatura, y para

${\displaystyle k={\frac {y''}{{\bigl (}1+{y'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}},}$

para la curvatura firmada.

En el caso general de una curva, el signo de la curvatura con signo es algo arbitrario, ya que depende de la orientación de la curva. En el caso de la gráfica de una función, existe una orientación natural al aumentar los valores de x . Esto hace significativo el signo de la curvatura con signo.

El signo de la curvatura con signo es el mismo que el signo de la segunda derivada de f . Si es positivo entonces la gráfica tiene una concavidad hacia arriba, y si es negativo la gráfica tiene una concavidad hacia abajo. Si es cero, entonces tenemos un punto de inflexión o un punto de ondulación .

Cuando la pendiente de la gráfica (es decir, la derivada de la función) es pequeña, la curvatura con signo se aproxima bien mediante la segunda derivada. Más precisamente, usando la notación O grande , se tiene

${\displaystyle k(x)=y''{\Bigl (}1+O{\bigl (}{\textstyle y'}^{2}{\bigr )}{\Bigr )}.}$

Es común en física e ingeniería aproximar la curvatura con la segunda derivada, por ejemplo, en la teoría de vigas o para derivar la ecuación de onda de una cuerda bajo tensión, y otras aplicaciones donde están involucradas pequeñas pendientes. Esto a menudo permite que sistemas que de otro modo serían no lineales sean tratados aproximadamente como lineales.

Coordenadas polares

Si una curva está definida en coordenadas polares por el radio expresado en función del ángulo polar, es decir r es función de θ , entonces su curvatura es

${\displaystyle \kappa (\theta )={\frac {\left|r^{2}+2{r'}^{2}-r\,r''\right|}{{\bigl (}r^{2}+{r'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}}}$

donde el primo se refiere a la diferenciación con respecto a θ .

Esto resulta de la fórmula de parametrizaciones generales, considerando la parametrización

${\displaystyle {\begin{aligned}x&=r(\theta )\cos \theta \\y&=r(\theta )\sin \theta \end{aligned}}}$

Curva implícita

Para una curva definida por una ecuación implícita F ( x , y ) = 0 con derivadas parciales denotadas F _x , F _y , F _xx , F _xy , F _yy , la curvatura viene dada por ^[7]

${\displaystyle \kappa ={\frac {\left|F_{y}^{2}F_{xx}-2F_{x}F_{y}F_{xy}+F_{x}^{2}F_{yy}\right|}{{\bigl (}F_{x}^{2}+F_{y}^{2}{\bigr )}{\vphantom {'}}^{3/2}}}.}$

La curvatura con signo no está definida, ya que depende de una orientación de la curva que no proporciona la ecuación implícita. Tenga en cuenta que cambiar F a – F no cambiaría la curva definida por F ( x , y ) = 0 , pero cambiaría el signo del numerador si se omitiera el valor absoluto en la fórmula anterior.

Un punto de la curva donde F _x = F _y = 0 es un punto singular , lo que significa que la curva no es diferenciable en este punto y, por lo tanto, que la curvatura no está definida (la mayoría de las veces, el punto es un punto de cruce o una cúspide ).

La fórmula anterior para la curvatura se puede derivar de la expresión de la curvatura de la gráfica de una función utilizando el teorema de la función implícita y el hecho de que, en dicha curva, se tiene

${\displaystyle {\frac {dy}{dx}}=-{\frac {F_{x}}{F_{y}}}.}$

Ejemplos

Puede resultar útil comprobar con ejemplos sencillos que las diferentes fórmulas dadas en las secciones anteriores dan el mismo resultado.

Círculo

Una parametrización común de un círculo de radio r es γ ( t ) = ( r cos t , r sin t ) . La fórmula para la curvatura da

${\displaystyle k(t)={\frac {r^{2}\sin ^{2}t+r^{2}\cos ^{2}t}{{\bigl (}r^{2}\cos ^{2}t+r^{2}\sin ^{2}t{\bigr )}{\vphantom {'}}^{3/2}}}={\frac {1}{r}}.}$

Se deduce, como se esperaba, que el radio de curvatura es el radio del círculo y que el centro de curvatura es el centro del círculo.

El círculo es un caso raro en el que la parametrización de la longitud del arco es fácil de calcular, ya que es

${\displaystyle {\boldsymbol {\gamma }}(s)=\left(r\cos {\frac {s}{r}},\,r\sin {\frac {s}{r}}\right).}$

Es una parametrización de longitud de arco, ya que la norma de

${\displaystyle {\boldsymbol {\gamma }}'(s)=\left(-\sin {\frac {s}{r}},\,\cos {\frac {s}{r}}\right)}$

es igual a uno. Esta parametrización da el mismo valor para la curvatura, ya que equivale a dividir por r ³ tanto en el numerador como en el denominador de la fórmula anterior.

El mismo círculo también se puede definir mediante la ecuación implícita F ( x , y ) = 0 con F ( x , y ) = x ² + y ² – r ² . Entonces, la fórmula para la curvatura en este caso da

${\displaystyle {\begin{aligned}\kappa &={\frac {\left|F_{y}^{2}F_{xx}-2F_{x}F_{y}F_{xy}+F_{x}^{2}F_{yy}\right|}{{\bigl (}F_{x}^{2}+F_{y}^{2}{\bigr )}{\vphantom {'}}^{3/2}}}\\&={\frac {8y^{2}+8x^{2}}{{\bigl (}4x^{2}+4y^{2}{\bigr )}{\vphantom {'}}^{3/2}}}\\&={\frac {8r^{2}}{{\bigl (}4r^{2}{\bigr )}{\vphantom {'}}^{3/2}}}={\frac {1}{r}}.\end{aligned}}}$

Parábola

Considere la parábola y = ax ² + bx + c .

Es la gráfica de una función, con derivada 2 ax + b y segunda derivada 2 a . Entonces, la curvatura con signo es

${\displaystyle k(x)={\frac {2a}{{\bigl (}1+\left(2ax+b\right)^{2}{\bigr )}{\vphantom {)}}^{3/2}}}.}$

Tiene el signo de a para todos los valores de x . Esto significa que, si a > 0 , la concavidad está dirigida hacia arriba en todas partes; si a < 0 , la concavidad está dirigida hacia abajo; para a = 0 , la curvatura es cero en todas partes, lo que confirma que la parábola degenera en una línea en este caso.

La curvatura (sin signo) es máxima para x = –b/2 un, es decir, en el punto estacionario (derivada cero) de la función, que es el vértice de la parábola.

Considere la parametrización γ ( t ) = ( t , en ² + bt + c ) = ( x , y ) . La primera derivada de x es 1 y la segunda derivada es cero. Sustituir en la fórmula para parametrizaciones generales da exactamente el mismo resultado que el anterior, con x reemplazado por t . Si usamos números primos para derivadas con respecto al parámetro t .

La misma parábola también se puede definir mediante la ecuación implícita F ( x , y ) = 0 con F ( x , y ) = ax ² + bx + c – y . Como F _y = –1 y F _yy = F _xy = 0 , se obtiene exactamente el mismo valor para la curvatura (sin signo). Sin embargo, la curvatura con signo no tiene sentido aquí, ya que – F ( x , y ) = 0 es una ecuación implícita válida para la misma parábola, que da el signo opuesto para la curvatura.

Fórmulas de Frenet-Serret para curvas planas

Los vectores T y N en dos puntos de una curva plana, una versión traducida del segundo cuadro (punteado) y δ T el cambio en T. Aquí δs es la distancia entre los puntos. en el limitere T/dsestará en dirección N. La curvatura describe la velocidad de rotación del marco.

La expresión de la curvatura en términos de parametrización de longitud de arco es esencialmente la primera fórmula de Frenet-Serret.

${\displaystyle \mathbf {T} '(s)=\kappa (s)\mathbf {N} (s),}$

donde los primos se refieren a las derivadas con respecto a la longitud del arco s , y N ( s ) es el vector unitario normal en la dirección de T ′(s) .

Como las curvas planas tienen torsión cero , la segunda fórmula de Frenet-Serret proporciona la relación

${\displaystyle {\begin{aligned}{\frac {d\mathbf {N} }{ds}}&=-\kappa \mathbf {T} ,\\&=-\kappa {\frac {d{\boldsymbol {\gamma }}}{ds}}.\end{aligned}}}$

Para una parametrización general mediante un parámetro t , se necesitan expresiones que incluyan derivadas con respecto a t . Como estos se obtienen multiplicando pords/dtlas derivadas con respecto a s , se tiene, para cualquier parametrización adecuada

${\displaystyle \mathbf {N} '(t)=-\kappa (t){\boldsymbol {\gamma }}'(t).}$

Peine de curvatura

Peine de curvatura

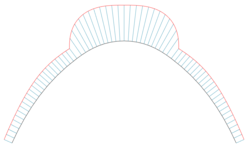
Se puede utilizar un peine de curvatura ^{[8] para representar gráficamente la curvatura de cada punto de una curva.} Si es una curva parametrizada su peine se define como la curva parametrizada ${\displaystyle t\mapsto x(t)}$

${\displaystyle t\mapsto x(t)+d\kappa (t)n(t)}$

donde están la curvatura y el vector normal y es un factor de escala (a elegir para mejorar la representación gráfica). ${\displaystyle \kappa ,n}$ ${\displaystyle d}$

Curvas espaciales

Animación de la curvatura y del vector aceleración T ′( s )

Como en el caso de las curvas en dos dimensiones, la curvatura de una curva espacial regular C en tres dimensiones (y superiores) es la magnitud de la aceleración de una partícula que se mueve con velocidad unitaria a lo largo de una curva. Por lo tanto, si γ ( s ) es la parametrización de longitud de arco de C , entonces el vector unitario tangente T ( s ) viene dado por

${\displaystyle \mathbf {T} (s)={\boldsymbol {\gamma }}'(s)}$

y la curvatura es la magnitud de la aceleración:

${\displaystyle \kappa (s)=\|\mathbf {T} '(s)\|=\|{\boldsymbol {\gamma }}''(s)\|.}$

La dirección de la aceleración es el vector normal unitario N ( s ) , que está definido por

${\displaystyle \mathbf {N} (s)={\frac {\mathbf {T} '(s)}{\|\mathbf {T} '(s)\|}}.}$

El plano que contiene los dos vectores T ( s ) y N ( s ) es el plano osculador de la curva en γ ( s ) . La curvatura tiene la siguiente interpretación geométrica. Existe un círculo en el plano osculador tangente a γ ( s ) cuya serie de Taylor de segundo orden en el punto de contacto concuerda con la de γ ( s ) . Este es el círculo osculador de la curva. El radio del círculo R ( s ) se llama radio de curvatura , y la curvatura es el recíproco del radio de curvatura:

${\displaystyle \kappa (s)={\frac {1}{R(s)}}.}$

La tangente, la curvatura y el vector normal juntos describen el comportamiento de segundo orden de una curva cerca de un punto. En tres dimensiones, el comportamiento de tercer orden de una curva se describe mediante una noción relacionada de torsión , que mide hasta qué punto una curva tiende a moverse como una trayectoria helicoidal en el espacio. La torsión y la curvatura están relacionadas por las fórmulas de Frenet-Serret (en tres dimensiones) y su generalización (en dimensiones superiores).

Expresiones generales

Para una curva espacial definida paramétricamente en tres dimensiones dada en coordenadas cartesianas por γ ( t ) = ( x ( t ), y ( t ), z ( t )) , la curvatura es

${\displaystyle \kappa ={\frac {\sqrt {{\bigl (}z''y'-y''z'{\bigr )}{\vphantom {'}}^{2}+{\bigl (}x''z'-z''x'{\bigr )}{\vphantom {'}}^{2}+{\bigl (}y''x'-x''y'{\bigr )}{\vphantom {'}}^{2}}}{{\bigl (}{x'}^{2}+{y'}^{2}+{z'}^{2}{\bigr )}{\vphantom {'}}^{3/2}}},}$

donde el número primo denota diferenciación con respecto al parámetro t . Esto se puede expresar independientemente del sistema de coordenadas mediante la fórmula ^[9]

${\displaystyle \kappa ={\frac {{\bigl \|}{\boldsymbol {\gamma }}'\times {\boldsymbol {\gamma }}''{\bigr \|}}{{\bigl \|}{\boldsymbol {\gamma }}'{\bigr \|}{\vphantom {'}}^{3}}}}$

donde × denota el producto vectorial vectorial . La siguiente fórmula es válida para la curvatura de curvas en un espacio euclidiano de cualquier dimensión:

${\displaystyle \kappa ={\frac {\sqrt {{\bigl \|}{\boldsymbol {\gamma }}'{\bigr \|}{\vphantom {'}}^{2}{\bigl \|}{\boldsymbol {\gamma }}''{\bigr \|}{\vphantom {'}}^{2}-{\bigl (}{\boldsymbol {\gamma }}'\cdot {\boldsymbol {\gamma }}''{\bigr )}{\vphantom {'}}^{2}}}{{\bigl \|}{\boldsymbol {\gamma }}'{\bigr \|}{\vphantom {'}}^{3}}}.}$

Curvatura del arco y longitud de la cuerda.

Dados dos puntos P y Q en C , sea s ( P , Q ) la longitud del arco de la porción de la curva entre P y Q y sea d ( P , Q ) la longitud del segmento de línea de P a Q. La curvatura de C en P viene dada por el límite ^{[ cita necesaria ] [10]}

${\displaystyle \kappa (P)=\lim _{Q\to P}{\sqrt {\frac {24{\bigl (}s(P,Q)-d(P,Q){\bigr )}}{s(P,Q){\vphantom {Q}}^{3}}}}}$

donde el límite se toma cuando el punto Q se aproxima a P en C. También se puede considerar que el denominador es d ( P , Q ) ³ . La fórmula es válida en cualquier dimensión. Además, al considerar el límite independientemente a cada lado de P , esta definición de curvatura a veces puede acomodar una singularidad en P. La fórmula sigue verificándola para el círculo osculador.

Superficies

La curvatura de curvas dibujadas sobre una superficie es la principal herramienta para definir y estudiar la curvatura de la superficie.

Curvas en superficies

Para una curva dibujada en una superficie (incrustada en un espacio euclidiano tridimensional ), se definen varias curvaturas, que relacionan la dirección de la curvatura con el vector normal unitario de la superficie , incluyendo:

• curvatura normal
• curvatura geodésica
• torsión geodésica

Cualquier curva no singular sobre una superficie lisa tiene su vector tangente T contenido en el plano tangente de la superficie. La curvatura normal , kn , es la curvatura de la curva proyectada sobre el plano que contiene la tangente de la curva _T y la superficie normal u ; la curvatura geodésica , k _g , es la curvatura de la curva proyectada sobre el plano tangente de la superficie; y la torsión geodésica (o torsión relativa ), τ _r , mide la tasa de cambio de la superficie normal alrededor de la tangente de la curva.

Sea la curva parametrizada en longitud de arco y sea t = u × T de modo que T , t , u formen una base ortonormal , llamada marco de Darboux . Las cantidades anteriores están relacionadas por:

${\displaystyle {\begin{pmatrix}\mathbf {T} '\\\mathbf {t} '\\\mathbf {u} '\end{pmatrix}}={\begin{pmatrix}0&\kappa _{\mathrm {g} }&\kappa _{\mathrm {n} }\\-\kappa _{\mathrm {g} }&0&\tau _{\mathrm {r} }\\-\kappa _{\mathrm {n} }&-\tau _{\mathrm {r} }&0\end{pmatrix}}{\begin{pmatrix}\mathbf {T} \\\mathbf {t} \\\mathbf {u} \end{pmatrix}}}$

Curvatura principal

Superficie de silla de montar con planos normales en direcciones de curvaturas principales

Todas las curvas en la superficie con el mismo vector tangente en un punto dado tendrán la misma curvatura normal, que es la misma que la curvatura de la curva obtenida al intersectar la superficie con el plano que contiene T y u . Tomando todos los vectores tangentes posibles, los valores máximo y mínimo de la curvatura normal en un punto se denominan curvaturas principales , k ₁ y k ₂ , y las direcciones de los vectores tangentes correspondientes se denominan direcciones normales principales .

Secciones normales

La curvatura se puede evaluar a lo largo de secciones normales de la superficie , similar a § Curvas en superficies superiores (consulte, por ejemplo, el radio de curvatura de la Tierra ).

Superficies desarrollables

Algunas superficies curvas, como las hechas de una hoja de papel lisa, se pueden aplanar en el plano sin distorsionar sus características intrínsecas de ninguna manera. Estas superficies desarrollables tienen curvatura gaussiana cero (ver más abajo). ^[11]

curvatura gaussiana

A diferencia de las curvas, que no tienen curvatura intrínseca, pero sí extrínseca (solo tienen curvatura dada una incrustación), las superficies pueden tener curvatura intrínseca, independientemente de una incrustación. La curvatura gaussiana , llamada así en honor a Carl Friedrich Gauss , es igual al producto de las curvaturas principales, k ₁ k ₂ . Tiene una dimensión de longitud ⁻² y es positiva para esferas , negativa para hiperboloides de una hoja y cero para planos y cilindros . Determina si una superficie es localmente convexa (cuando es positiva) o localmente tiene forma de silla de montar (cuando es negativa).

La curvatura gaussiana es una propiedad intrínseca de la superficie, lo que significa que no depende de la incrustación particular de la superficie; Intuitivamente, esto significa que las hormigas que viven en la superficie podrían determinar la curvatura gaussiana. Por ejemplo, una hormiga que viviera en una esfera podría medir la suma de los ángulos interiores de un triángulo y determinar que era mayor a 180 grados, implicando que el espacio que habitaba tenía curvatura positiva. Por otra parte, una hormiga que viviera en un cilindro no detectaría tal desviación de la geometría euclidiana ; en particular, la hormiga no pudo detectar que las dos superficies tienen curvaturas medias diferentes (ver más abajo), que es un tipo de curvatura puramente extrínseca.

Formalmente, la curvatura gaussiana sólo depende de la métrica de Riemann de la superficie. Este es el célebre Theorema Egregium de Gauss , que encontró mientras se ocupaba de los estudios geográficos y la cartografía.

Una definición intrínseca de la curvatura gaussiana en un punto P es la siguiente: imaginemos una hormiga que está atada a P con un hilo corto de longitud r . Corre alrededor de P mientras el hilo está completamente estirado y mide la longitud C ( r ) de un viaje completo alrededor de P. Si la superficie fuera plana, la hormiga encontraría C ( r ) = 2π r . En superficies curvas, la fórmula para C ( r ) será diferente, y la curvatura gaussiana K en el punto P se puede calcular mediante el teorema de Bertrand-Diguet-Puiseux como

${\displaystyle K=\lim _{r\to 0^{+}}3\left({\frac {2\pi r-C(r)}{\pi r^{3}}}\right).}$

La integral de la curvatura gaussiana sobre toda la superficie está estrechamente relacionada con la característica de Euler de la superficie ; ver el teorema de Gauss-Bonnet .

El análogo discreto de la curvatura, correspondiente a la curvatura concentrada en un punto y particularmente útil para los poliedros , es el defecto (angular) ; El análogo del teorema de Gauss-Bonnet es el teorema de Descartes sobre el defecto angular total .

Debido a que la curvatura (gaussiana) se puede definir sin referencia a un espacio de incrustación, no es necesario que una superficie esté incrustada en un espacio de dimensiones superiores para poder ser curvada. Una superficie bidimensional tan intrínsecamente curvada es un ejemplo simple de variedad de Riemann .

Curvatura media

La curvatura media es una medida extrínseca de curvatura igual a la mitad de la suma de las curvaturas principales ,k ₁ + k ₂/2. Tiene una dimensión de longitud ⁻¹ . La curvatura media está estrechamente relacionada con la primera variación del área de superficie . En particular, una superficie mínima , como una película de jabón, tiene una curvatura media cero y una pompa de jabón tiene una curvatura media constante. A diferencia de la curvatura de Gauss, la curvatura media es extrínseca y depende de la incrustación, por ejemplo, un cilindro y un plano son localmente isométricos pero la curvatura media de un plano es cero mientras que la de un cilindro es distinta de cero.

Segunda forma fundamental

La curvatura intrínseca y extrínseca de una superficie se puede combinar en la segunda forma fundamental. Esta es una forma cuadrática en el plano tangente a la superficie en un punto cuyo valor en un vector tangente particular X a la superficie es el componente normal de la aceleración de una curva a lo largo de la superficie tangente a X ; es decir, es la curvatura normal a una curva tangente a X (ver arriba). Simbólicamente,

${\displaystyle \operatorname {I\!I} (\mathbf {X} ,\mathbf {X} )=\mathbf {N} \cdot (\nabla _{\mathbf {X} }\mathbf {X} )}$

donde N es la unidad normal a la superficie. Para vectores unitarios tangentes X , la segunda forma fundamental asume el valor máximo k ₁ y el valor mínimo k ₂ , que ocurren en las direcciones principales u ₁ y u ₂ , respectivamente. Así, según el teorema del eje principal , la segunda forma fundamental es

${\displaystyle \operatorname {I\!I} (\mathbf {X} ,\mathbf {X} )=k_{1}\left(\mathbf {X} \cdot \mathbf {u} _{1}\right)^{2}+k_{2}\left(\mathbf {X} \cdot \mathbf {u} _{2}\right)^{2}.}$

Así, la segunda forma fundamental codifica tanto la curvatura intrínseca como la extrínseca.

Operador de forma

Se puede encontrar una encapsulación de la curvatura de la superficie en el operador de forma, S , que es un operador lineal autoadjunto desde el plano tangente a sí mismo (específicamente, el diferencial del mapa de Gauss ).

Para una superficie con vectores tangentes X y normal N , el operador de forma se puede expresar de forma compacta en notación de suma de índices como

${\displaystyle \partial _{a}\mathbf {N} =-S_{ba}\mathbf {X} _{b}.}$

(Compare la expresión alternativa de curvatura para una curva plana).

Las ecuaciones de Weingarten dan el valor de S en términos de los coeficientes de la primera y segunda forma fundamental como

${\displaystyle S=\left(EG-F^{2}\right)^{-1}{\begin{pmatrix}eG-fF&fG-gF\\fE-eF&gE-fF\end{pmatrix}}.}$

Las curvaturas principales son los valores propios del operador de forma, las direcciones de curvatura principales son sus vectores propios , la curvatura de Gauss es su determinante y la curvatura media es la mitad de su traza .

Curvatura del espacio

Por extensión del argumento anterior, un espacio de tres o más dimensiones puede ser intrínsecamente curvo. La curvatura es intrínseca en el sentido de que es una propiedad definida en cada punto del espacio, más que una propiedad definida con respecto a un espacio mayor que lo contiene. En general, un espacio curvo puede concebirse o no como incrustado en un espacio ambiental de dimensiones superiores ; de lo contrario, su curvatura sólo puede definirse intrínsecamente.

Después del descubrimiento de la definición intrínseca de curvatura, que está estrechamente relacionada con la geometría no euclidiana , muchos matemáticos y científicos se preguntaron si el espacio físico ordinario podría ser curvo, aunque el éxito de la geometría euclidiana hasta ese momento significaba que el radio de curvatura debía ser curvado. ser astronómicamente grande. En la teoría de la relatividad general , que describe la gravedad y la cosmología , la idea se generaliza ligeramente a la "curvatura del espacio-tiempo "; En la teoría de la relatividad, el espacio-tiempo es una variedad pseudo-riemanniana . Una vez definida una coordenada de tiempo, el espacio tridimensional correspondiente a un tiempo particular es generalmente una variedad de Riemann curva; pero dado que la elección de las coordenadas temporales es en gran medida arbitraria, es la curvatura del espacio-tiempo subyacente la que es físicamente significativa.

Aunque un espacio arbitrariamente curvo es muy complejo de describir, la curvatura de un espacio que es localmente isotrópico y homogéneo se describe mediante una única curvatura gaussiana, como para una superficie; Matemáticamente estas son condiciones fuertes, pero corresponden a suposiciones físicas razonables (todos los puntos y todas las direcciones son indistinguibles). Una curvatura positiva corresponde al radio de curvatura del cuadrado inverso; un ejemplo es una esfera o hiperesfera . Un ejemplo de espacio con curvatura negativa es la geometría hiperbólica (ver también: curvatura no positiva ). Se llama plano a un espacio o espacio-tiempo con curvatura nula .Por ejemplo, el espacio euclidiano es un ejemplo de espacio plano y el espacio de Minkowski es un ejemplo de espaciotiempo plano. Sin embargo, hay otros ejemplos de geometrías planas en ambos entornos. A un toroide o a un cilindro se les pueden dar métricas planas, pero difieren en su topología . También son posibles otras topologías para espacios curvos (ver también: Forma del universo ) .

Generalizaciones

Mover un vector a lo largo de una curva desde A → N → B → A produce otro vector. La imposibilidad de volver al vector inicial se mide por la holonomía de la superficie. En un espacio sin curvatura, el ángulo α es de 0 grados, y en un espacio con curvatura, el ángulo α es mayor que 0 grados. Cuanto más curvado es el espacio, mayor es la magnitud del ángulo α.

La noción matemática de curvatura también se define en contextos mucho más generales. ^[12] Muchas de estas generalizaciones enfatizan diferentes aspectos de la curvatura tal como se entiende en dimensiones inferiores.

Una de esas generalizaciones es cinemática. Naturalmente, la curvatura de una curva puede considerarse como una cantidad cinemática, que representa la fuerza que siente un determinado observador que se mueve a lo largo de la curva; De manera análoga, la curvatura en dimensiones superiores puede considerarse como una especie de fuerza de marea (esta es una forma de pensar en la curvatura seccional ). Esta generalización de la curvatura depende de cómo las partículas de prueba cercanas divergen o convergen cuando se les permite moverse libremente en el espacio; ver campo de Jacobi .

Otra amplia generalización de la curvatura proviene del estudio del transporte paralelo sobre una superficie. Por ejemplo, si un vector se mueve alrededor de un bucle en la superficie de una esfera manteniéndose paralelo durante todo el movimiento, entonces la posición final del vector puede no ser la misma que la posición inicial del vector. Este fenómeno se conoce como holonomía . ^[13] Varias generalizaciones capturan de forma abstracta esta idea de curvatura como medida de holonomía; ver forma de curvatura . Una noción de curvatura estrechamente relacionada proviene de la teoría de calibre en física, donde la curvatura representa un campo y un potencial vectorial para el campo es una cantidad que en general depende de la trayectoria: puede cambiar si un observador se mueve alrededor de un bucle.

Dos generalizaciones más de la curvatura son la curvatura escalar y la curvatura de Ricci . En una superficie curva como la esfera, el área de un disco en la superficie difiere del área de un disco del mismo radio en un espacio plano. Esta diferencia (en un límite adecuado) se mide por la curvatura escalar. La diferencia de área de un sector del disco se mide mediante la curvatura de Ricci. Cada una de las curvaturas escalares y curvaturas de Ricci se definen de manera análoga en tres dimensiones y superiores. Son particularmente importantes en la teoría de la relatividad, donde ambos aparecen en el lado de las ecuaciones de campo de Einstein que representa la geometría del espacio-tiempo (el otro lado representa la presencia de materia y energía). Estas generalizaciones de la curvatura subyacen, por ejemplo, a la noción de que la curvatura puede ser una propiedad de una medida ; ver curvatura de una medida .

Otra generalización de la curvatura se basa en la capacidad de comparar un espacio curvo con otro espacio que tiene curvatura constante . A menudo esto se hace con triángulos en los espacios. La noción de triángulo tiene sentido en espacios métricos , y esto da lugar a espacios CAT( k ) .

Ver también

• Forma de curvatura para la noción apropiada de curvatura para haces de vectores y haces principales con conexión
• Curvatura de una medida para una noción de curvatura en la teoría de la medida.
• Curvatura de superficies paramétricas.
• Curvatura de variedades de Riemann para generalizaciones de la curvatura de Gauss a variedades de Riemann de dimensiones superiores
• Vector de curvatura y curvatura geodésica para nociones apropiadas de curvatura de curvas en variedades de Riemann, de cualquier dimensión.
• Grado de curvatura
• Geometría diferencial de curvas para un tratamiento completo de curvas incrustadas en un espacio euclidiano de dimensión arbitraria.
• Dioptría , una medida de curvatura utilizada en óptica
• Evoluta , el lugar geométrico de los centros de curvatura de una curva dada.
• Teorema fundamental de las curvas
• Teorema de Gauss-Bonnet para una aplicación elemental de la curvatura
• Mapa de Gauss para más propiedades geométricas de la curvatura de Gauss
• Principio de mínima restricción de Gauss , una expresión del principio de mínima acción
• Curvatura media en un punto de una superficie.
• Radio mínimo de curvatura ferroviaria
• Radio de curvatura
• Segunda forma fundamental para la curvatura extrínseca de hipersuperficies en general.
• Sinuosidad
• torsión de una curva

Notas

1. Clagett, Marshall (1968), Nicole Oresme y la geometría medieval de cualidades y movimientos; un tratado sobre la uniformidad y difformidad de las intensidades conocido como Tractatus de Configurationibus qualitatum et motuum., Madison, WI: Prensa de la Universidad de Wisconsin, ISBN 0-299-04880-2
2. Serrano, Isabel; Suceavă, Bogdan (2015). "Un misterio medieval: el concepto de Curvitas de Nicole Oresme" (PDF) . Avisos de la Sociedad Matemática Estadounidense . 62 (9): 1030–1034. doi : 10.1090/noti1275 .
3. Borovik, Alejandro ; Katz, Mikhail G. (2011), "¿Quién te contó el cuento de Cauchy-Weierstrass? La historia dual del cálculo riguroso", Fundamentos de la ciencia , 17 (3): 245–276, arXiv : 1108.2885 , Bibcode : 2011arXiv1108.2885B, doi :10.1007/s10699-011-9235-x, S2CID  119320059
4. Pressley, Andrés. Geometría diferencial elemental (1ª ed.). pag. 29.
5. Kline, Morris. Cálculo: un enfoque físico e intuitivo (2ª ed.). pag. 458.
6. Kennedy, John (2011). "La parametrización de la longitud del arco de una curva". Archivado desde el original el 28 de septiembre de 2015 . Consultado el 10 de diciembre de 2013 .
7. Goldman, Ron (2005). "Fórmulas de curvatura para superficies y curvas implícitas". Diseño Geométrico Asistido por Computadora . 22 (7): 632–658. CiteSeerX 10.1.1.413.3008 . doi :10.1016/j.cagd.2005.06.005. 
8. Farín, Gerald (2016). "Peines de curvatura y trazados de curvatura". Diseño asistido por ordenador . 80 : 6–8. doi :10.1016/j.cad.2016.08.003.
9. Se puede encontrar una prueba de esto en el artículo sobre curvatura en Wolfram MathWorld .
10. Bitetto, Marco (26 de noviembre de 2018). "Dinámica hiperespacial". Nova Università di Engeneria e Scienza : 206.
11. superficie desarrollable, Mathworld. (Consultado el 11 de febrero de 2021)
12. Kobayashi, Shoshichi ; Nomizu, Katsumi . Fundamentos de Geometría Diferencial . Wiley Interciencia . vol. 1 cap. 2–3.
13. Henderson, David W .; Taimiņa, Daina . Experimentar la geometría (3ª ed.). págs. 98–99.

Referencias

• Coolidge, Julian L. (junio de 1952). "La insatisfactoria historia de la curvatura". Mensual Matemático Estadounidense . 59 (6): 375–379. doi :10.2307/2306807. JSTOR  2306807.
• Sokolov, Dmitriĭ Dmitrievich (2001) [1994], "Curvatura", Enciclopedia de Matemáticas , EMS Press
• Kline, Morris (1998). Cálculo: un enfoque físico e intuitivo . Dover. págs. 457–461. ISBN 978-0-486-40453-0.( copia restringida en línea , p. 457, en Google Books )
• Klaf, A. Albert (1956). Actualización de cálculo . Dover. págs. 151-168. ISBN 978-0-486-20370-6.( copia restringida en línea , p. 151, en Google Books )
• Casey, James (1996). Explorando la curvatura . Vieweg+Teubner. ISBN 978-3-528-06475-4.

enlaces externos

• Las conferencias Feynman sobre física vol. II Cap. 42: Espacio curvo
• La historia de la curvatura
• Curvatura, intrínseca y extrínseca en MathPages