Ecuación de onda

Ecuación diferencial importante en física.

La ecuación de onda es una ecuación diferencial parcial lineal de segundo orden para la descripción de ondas o campos de ondas estacionarias , como ondas mecánicas (p. ej. , ondas de agua , ondas sonoras y ondas sísmicas ) u ondas electromagnéticas (incluidas las ondas de luz ). Surge en campos como la acústica , el electromagnetismo y la dinámica de fluidos .

Este artículo se centra en las ondas bidireccionales en la física clásica . Las ondas mecánicas o electromagnéticas individuales que se propagan en una dirección predefinida también se pueden describir con la ecuación de onda unidireccional de primer orden , que es mucho más fácil de resolver y también válida para medios no homogéneos. La física cuántica utiliza una ecuación de onda basada en operadores a menudo como una ecuación de onda relativista .

Introducción

La ecuación de onda (bidireccional) es una ecuación diferencial parcial de segundo orden que describe ondas, incluidas las ondas viajeras y estacionarias ; estos últimos pueden considerarse como superposiciones lineales de ondas que viajan en direcciones opuestas. Este artículo se centra principalmente en la ecuación de onda escalar que describe ondas en escalares mediante funciones escalares u = u (x, y, z, t) de una variable de tiempo t (una variable que representa el tiempo) y una o más variables espaciales x, y, z. (variables que representan una posición en un espacio en discusión), mientras que existen ecuaciones de ondas vectoriales que describen ondas en vectores como ondas para un campo eléctrico, campo magnético y potencial vectorial magnético y ondas elásticas. En comparación con las ecuaciones de ondas vectoriales, la ecuación de ondas escalares puede verse como un caso especial de las ecuaciones de ondas vectoriales; En el sistema de coordenadas cartesiano , la ecuación de onda escalar es la ecuación que debe satisfacer cada componente (para cada eje de coordenadas, como la componente x para el eje x ) de una onda vectorial sin fuentes de ondas en el dominio considerado (es decir, un espacio y un tiempo). Por ejemplo, en el sistema de coordenadas cartesiano, como representación de una onda de campo vectorial eléctrico en ausencia de fuentes de onda, cada componente del eje de coordenadas ( i = x , y , z ) debe satisfacer la ecuación de onda escalar. Otras soluciones de ecuaciones de ondas escalares u son para cantidades físicas en escalares , como la presión en un líquido o gas, o el desplazamiento a lo largo de alguna dirección específica de partículas de un sólido vibrante lejos de sus posiciones de reposo (equilibrio). ${\displaystyle (E_{x},E_{y},E_{z})}$ ${\displaystyle {\vec {E}}}$ ${\displaystyle E_{i}}$

La ecuación de onda escalar es

$${\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}=c^{2}\left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}\right),}$$

c es un coeficiente real

En otras palabras:

• u es el factor que representa un desplazamiento de la situación de reposo; podría ser la presión del gas por encima o por debajo de lo normal, o la altura del agua en un estanque por encima o por debajo del reposo, o cualquier otra cosa.
• t representa el tiempo.
• ${\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}}$es un término que describe la fuerza con la que se cambia el desplazamiento.
• x representa el espacio o la posición.
• ${\displaystyle {\frac {\partial ^{2}u}{\partial x_{1}^{2}}}}$es un término que describe cómo varía el desplazamiento en el punto x en una de las dimensiones (como uno de los ejes de una gráfica). No es la velocidad a la que el desplazamiento cambia a través del espacio, sino de hecho la velocidad a la que el cambio mismo cambia a través del espacio: su segunda derivada . En otras palabras, este término muestra cómo los cambios del desplazamiento se concentran en un área circundante minúscula.

La ecuación establece que en cualquier caso dado, en cualquier punto dado, la forma en que se acelera el desplazamiento es proporcional a la forma en que los cambios del desplazamiento se aplastan en el área circundante. O, en términos aún más simples: un desplazamiento más puntiagudo es rechazado con más fuerza.

Usando las notaciones de la mecánica newtoniana y el cálculo vectorial , la ecuación de onda se puede escribir de manera más compacta como

${\displaystyle {\ddot {u}}=c^{2}\nabla ^{2}u,}$

donde el doble punto denota doble derivada temporal de u , ∇ es el operador nabla y ∇ ² = ∇ · ∇ es el operador laplaciano (espacial) (no laplaciano vectorial): ${\displaystyle {\ddot {u}}}$

$${\displaystyle {\ddot {u}}={\frac {\partial ^{2}u}{\partial t^{2}}},\qquad \nabla =\left({\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}},{\frac {\partial }{\partial z}}\right),\qquad \nabla ^{2}={\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}+{\frac {\partial ^{2}}{\partial z^{2}}}.}$$

Una notación aún más compacta que a veces se usa en física se lee simplemente

$${\displaystyle \Box u=0,}$$

operador d'Alembert

$${\displaystyle \Box ={\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}-\nabla ^{2}.}$$

Una solución de esta ecuación de onda (bidireccional) puede ser bastante complicada, pero puede analizarse como una combinación lineal de soluciones simples que son ondas planas sinusoidales con varias direcciones de propagación y longitudes de onda, pero todas con la misma velocidad de propagación c . Este análisis es posible porque la ecuación de onda es lineal y homogénea, de modo que cualquier múltiplo de una solución también es una solución, y la suma de dos soluciones cualesquiera es nuevamente una solución. Esta propiedad se llama principio de superposición en física.

La ecuación de onda por sí sola no especifica una solución física; Por lo general, se obtiene una solución única planteando un problema con condiciones adicionales, como las condiciones iniciales , que prescriben la amplitud y la fase de la onda. Otra clase importante de problemas ocurre en espacios cerrados especificados por condiciones de contorno , cuyas soluciones representan ondas estacionarias o armónicos , análogos a los armónicos de los instrumentos musicales.

La ecuación de onda bidireccional, que describe un campo de onda estacionaria, es el ejemplo más simple de una ecuación diferencial hiperbólica de segundo orden . Éste y sus modificaciones desempeñan papeles fundamentales en la mecánica del continuo , la mecánica cuántica , la física del plasma , la relatividad general , la geofísica y muchas otras disciplinas científicas y técnicas.  En el caso de que sólo sea de interés la propagación de una única onda en una dirección predefinida, se puede considerar una ecuación diferencial parcial de primer orden ( ecuación de onda unidireccional ).

Ecuación de onda en una dimensión espacial.

El científico francés Jean-Baptiste le Rond d'Alembert descubrió la ecuación de onda en una dimensión espacial. ^[1]

La ecuación de onda en una dimensión espacial se puede escribir de la siguiente manera:

$${\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}=c^{2}{\frac {\partial ^{2}u}{\partial x^{2}}}.}$$

Generalmente se describe que esta ecuación tiene una sola dimensión espacial x , porque la única otra variable independiente es el tiempo t . Sin embargo, la variable dependiente u puede representar una segunda dimensión espacial si, por ejemplo, el desplazamiento u se produce en la dirección y , como en el caso de una cuerda que se encuentra en el plano xy .

Derivación de la ecuación de onda.

La ecuación de onda en una dimensión espacial se puede derivar en una variedad de entornos físicos diferentes. Lo más famoso es que se puede derivar para el caso de una cuerda que vibra en un plano bidimensional, con cada uno de sus elementos tirados en direcciones opuestas por la fuerza de tensión . ^[2]

Otro escenario físico para la derivación de la ecuación de onda en una dimensión espacial utiliza la ley de Hooke . En la teoría de la elasticidad , la ley de Hooke es una aproximación para ciertos materiales, afirmando que la cantidad en la que se deforma un cuerpo material (la deformación ) está linealmente relacionada con la fuerza que causa la deformación (la tensión ).

De la ley de Hooke

La ecuación de onda en el caso unidimensional se puede derivar de la ley de Hooke de la siguiente manera: imagine un conjunto de pequeños pesos de masa m interconectados con resortes sin masa de longitud h . Los resortes tienen una constante elástica de k :

Aquí la variable dependiente u ( x ) mide la distancia desde el equilibrio de la masa situada en x , de modo que u ( x ) esencialmente mide la magnitud de una perturbación (es decir, deformación) que se desplaza en un material elástico. La fuerza resultante ejercida sobre la masa m en el lugar x + h es:

$${\displaystyle {\begin{aligned}F_{\text{Hooke}}&=F_{x+2h}-F_{x}=k[u(x+2h,t)-u(x+h,t)]-k[u(x+h,t)-u(x,t)].\end{aligned}}}$$

Al equiparar esta última ecuación con

$${\displaystyle {\begin{aligned}F_{\text{Newton}}&=m\,a(t)=m\,{\frac {\partial ^{2}}{\partial t^{2}}}u(x+h,t),\end{aligned}}}$$

Se obtiene la ecuación de movimiento para el peso en el lugar x + h :

$${\displaystyle {\frac {\partial ^{2}}{\partial t^{2}}}u(x+h,t)={\frac {k}{m}}[u(x+2h,t)-u(x+h,t)-u(x+h,t)+u(x,t)].}$$

NL = NhM = Nmconstante elásticaK = k / N

$${\displaystyle {\frac {\partial ^{2}}{\partial t^{2}}}u(x+h,t)={\frac {KL^{2}}{M}}{\frac {u(x+2h,t)-2u(x+h,t)+u(x,t)}{h^{2}}}.}$$

Tomando el límite N → ∞, h → 0 y suponiendo suavidad, se obtiene

$${\displaystyle {\frac {\partial ^{2}u(x,t)}{\partial t^{2}}}={\frac {KL^{2}}{M}}{\frac {\partial ^{2}u(x,t)}{\partial x^{2}}},}$$

segunda derivadaKL ² / M

Onda estacionaria unidimensional como superposición de dos ondas que viajan en direcciones opuestas

Pulso de estrés en un bar.

En el caso de un pulso de tensión que se propaga longitudinalmente a través de una barra, la barra actúa de manera muy similar a un número infinito de resortes en serie y puede tomarse como una extensión de la ecuación derivada de la ley de Hooke. Una barra uniforme, es decir, de sección transversal constante, hecha de un material elástico lineal tiene una rigidez K dada por

$${\displaystyle K={\frac {EA}{L}},}$$

AEmódulo de Young

$${\displaystyle {\frac {\partial ^{2}u(x,t)}{\partial t^{2}}}={\frac {EAL}{M}}{\frac {\partial ^{2}u(x,t)}{\partial x^{2}}}.}$$

AL es igual al volumen de la barra, y por lo tanto

$${\displaystyle {\frac {AL}{M}}={\frac {1}{\rho }},}$$

ρ

$${\displaystyle {\frac {\partial ^{2}u(x,t)}{\partial t^{2}}}={\frac {E}{\rho }}{\frac {\partial ^{2}u(x,t)}{\partial x^{2}}}.}$$

Por tanto, la velocidad de una onda de tensión en una barra es . ${\displaystyle {\sqrt {E/\rho }}}$

solución general

Enfoque algebraico

La ecuación de onda unidimensional es inusual para una ecuación diferencial parcial porque se puede encontrar una solución general relativamente simple. Definiendo nuevas variables ^[3]

$${\displaystyle {\begin{aligned}\xi &=x-ct,\\\eta &=x+ct\end{aligned}}}$$

$${\displaystyle {\frac {\partial ^{2}u}{\partial \xi \partial \eta }}(x,t)=0,}$$

$${\displaystyle u(x,t)=F(\xi )+G(\eta ),}$$

$${\displaystyle u(x,t)=F(x-ct)+G(x+ct).}$$

En otras palabras, las soluciones de la ecuación de onda 1D son sumas de una función F que viaja hacia la derecha y una función G que viaja hacia la izquierda . "Viajar" significa que la forma de estas funciones arbitrarias individuales con respecto a x permanece constante; sin embargo, las funciones se trasladan hacia la izquierda y hacia la derecha con el tiempo a la velocidad c . Esto fue derivado por Jean le Rond d'Alembert . ^[4]

Otra forma de llegar a este resultado es factorizar la ecuación de onda utilizando dos operadores diferenciales de primer orden:

$${\displaystyle \left[{\frac {\partial }{\partial t}}-c{\frac {\partial }{\partial x}}\right]\left[{\frac {\partial }{\partial t}}+c{\frac {\partial }{\partial x}}\right]u=0.}$$

ecuaciones de onda unidireccionales

$${\displaystyle {\frac {\partial w}{\partial t}}-c{\frac {\partial w}{\partial x}}=0,\qquad {\frac {\partial w}{\partial t}}+c{\frac {\partial w}{\partial x}}=0.}$$

Entonces, para nuestra ecuación original, podemos definir

$${\displaystyle v\equiv {\frac {\partial u}{\partial t}}+c{\frac {\partial u}{\partial x}},}$$

$${\displaystyle {\frac {\partial v}{\partial t}}-c{\frac {\partial v}{\partial x}}=0.}$$

Esta ecuación de onda unidireccional se puede resolver interpretándola como si nos dijera que la derivada direccional de v en la dirección (1, -c ) es 0. Esto significa que el valor de v es constante en las líneas características de la forma x + ct = x ₀ , y por tanto que v debe depender sólo de x + ct , es decir, tener la forma H ( x + ct ) . Luego, para resolver la primera ecuación de onda unidireccional (no homogénea) que relaciona v con u , podemos observar que su solución homogénea debe ser una función de la forma F ( x - ct ) , por una lógica similar a la anterior. Adivinando una solución particular de la forma G ( x + ct ) , encontramos que

$${\displaystyle \left[{\frac {\partial }{\partial t}}+c{\frac {\partial }{\partial x}}\right]G(x+ct)=H(x+ct).}$$

Expandir el lado izquierdo, reorganizar los términos y luego usar el cambio de variables s = x + ct simplifica la ecuación a

$${\displaystyle G'(s)={\frac {H(s)}{2c}}.}$$

Esto significa que podemos encontrar una solución particular G de la forma deseada por integración. Por lo tanto, hemos demostrado nuevamente que u obedece a u ( x , t ) = F ( x - ct ) + G ( x + ct ) mediante ecuaciones de onda unidireccionales. ^[5] Tenga en cuenta que, dado que los operadores diferenciales de onda unidireccional conmutan para funciones analíticas según el teorema de Clairaut , podríamos haber configurado de manera equivalente nuestro sistema de ecuaciones de onda unidireccional para resolverlas en el orden opuesto.

La ecuación de onda habitual de segundo orden a veces se denomina "ecuación de onda bidireccional" (superposición de dos ondas) para distinguirla de la ecuación de onda unidireccional de primer orden que describe la propagación de una sola onda en un entorno predefinido. dirección.

Para un problema de valores iniciales , se pueden determinar las funciones arbitrarias F y G para satisfacer las condiciones iniciales:

$${\displaystyle u(x,0)=f(x),}$$

$${\displaystyle u_{t}(x,0)=g(x).}$$

El resultado es la fórmula de d'Alembert :

$${\displaystyle u(x,t)={\frac {f(x-ct)+f(x+ct)}{2}}+{\frac {1}{2c}}\int _{x-ct}^{x+ct}g(s)\,ds.}$$

En el sentido clásico, si f ( x ) ∈ C ^k y g ( x ) ∈ C ^{k −1} , entonces u ( t , x ) ∈ C ^k . Sin embargo, las formas de onda F y G también pueden ser funciones generalizadas , como la función delta. En ese caso, la solución puede interpretarse como un impulso que viaja hacia la derecha o hacia la izquierda.

La ecuación de onda básica es una ecuación diferencial lineal , por lo que seguirá el principio de superposición . Esto significa que el desplazamiento neto causado por dos o más olas es la suma de los desplazamientos que habría causado cada ola individualmente. Además, el comportamiento de una onda se puede analizar dividiéndola en componentes, por ejemplo, la transformada de Fourier descompone una onda en componentes sinusoidales.

Modos propios de onda plana

Otra forma de resolver la ecuación de onda unidimensional es analizar primero sus modos propios de frecuencia . Un llamado modo propio es una solución que oscila en el tiempo con una frecuencia angular constante bien definida ω , de modo que la parte temporal de la función de onda toma la forma e ^{− iωt} = cos( ωt ) − i sin( ωt ) , y la amplitud es una función f ( x ) de la variable espacial x , dando una separación de variables para la función de onda:

$${\displaystyle u_{\omega }(x,t)=e^{-i\omega t}f(x).}$$

Esto produce una ecuación diferencial ordinaria para la parte espacial f ( x ) :

$${\displaystyle {\frac {\partial ^{2}u_{\omega }}{\partial t^{2}}}={\frac {\partial ^{2}}{\partial t^{2}}}\left(e^{-i\omega t}f(x)\right)=-\omega ^{2}e^{-i\omega t}f(x)=c^{2}{\frac {\partial ^{2}}{\partial x^{2}}}\left(e^{-i\omega t}f(x)\right).}$$

Por lo tanto,

$${\displaystyle {\frac {d^{2}}{dx^{2}}}f(x)=-\left({\frac {\omega }{c}}\right)^{2}f(x),}$$

ecuación de valor propiof ( x )ecuación de Helmholtzde onda plana

$${\displaystyle f(x)=Ae^{\pm ikx},}$$

número de onda k = ω / c

La función de onda total para este modo propio es entonces la combinación lineal

$${\displaystyle u_{\omega }(x,t)=e^{-i\omega t}\left(Ae^{-ikx}+Be^{ikx}\right)=Ae^{-i(kx+\omega t)}+Be^{i(kx-\omega t)},}$$

AB

Los modos propios son útiles para construir una solución completa a la ecuación de onda, porque cada uno de ellos evoluciona trivialmente en el tiempo con el factor de fase, de modo que una solución completa se puede descomponer en una expansión de modo propio : ${\displaystyle e^{-i\omega t},}$

$${\displaystyle u(x,t)=\int _{-\infty }^{\infty }s(\omega )u_{\omega }(x,t)\,d\omega ,}$$

$${\displaystyle {\begin{aligned}u(x,t)&=\int _{-\infty }^{\infty }s_{+}(\omega )e^{-i(kx+\omega t)}\,d\omega +\int _{-\infty }^{\infty }s_{-}(\omega )e^{i(kx-\omega t)}\,d\omega \\&=\int _{-\infty }^{\infty }s_{+}(\omega )e^{-ik(x+ct)}\,d\omega +\int _{-\infty }^{\infty }s_{-}(\omega )e^{ik(x-ct)}\,d\omega \\&=F(x-ct)+G(x+ct),\end{aligned}}}$$

s _± ( ω )componente de Fourieren el dominio de la frecuenciaen el dominio del tiempoFDTDpaquete de ondas u ( x ,  t )chirriadasω^[6]anomalía de sobrevuelo

Ecuación de onda vectorial en tres dimensiones espaciales.

La ecuación de onda vectorial (de la cual se puede derivar directamente la ecuación de onda escalar) se puede obtener aplicando un equilibrio de fuerzas a un elemento de volumen infinitesimal. En un continuo homogéneo (coordenada cartesiana ) con un módulo de elasticidad constante , una deflexión elástica vectorial provoca el tensor de tensión . El equilibrio local de a) la fuerza de tensión debida a la deflexión y b) la fuerza de inercia causada por la aceleración local se puede escribir como ${\displaystyle \mathbf {x} }$ ${\displaystyle E}$ ${\displaystyle \mathbf {u} (\mathbf {x} ,t)}$ ${\displaystyle \mathbf {T} =E\nabla \mathbf {u} }$ ${\displaystyle \operatorname {div} \mathbf {T} =\nabla \cdot (E\nabla \mathbf {u} )=E\Delta \mathbf {u} }$ ${\displaystyle \mathbf {u} }$ ${\displaystyle \rho \partial ^{2}\mathbf {u} /\partial t^{2}}$ ${\displaystyle \partial ^{2}\mathbf {u} /\partial t^{2}}$

$${\displaystyle \rho {\frac {\partial ^{2}\mathbf {u} }{\partial t^{2}}}-E\Delta \mathbf {u} =\mathbf {0} .}$$

^[7] ${\displaystyle \rho }$ ${\displaystyle E,}$ ${\displaystyle c={\sqrt {E/\rho }}}$

$${\displaystyle {\frac {\partial ^{2}\mathbf {u} }{\partial t^{2}}}-c^{2}\Delta \mathbf {u} ={\boldsymbol {0}}.}$$

${\displaystyle \mathbf {u} (\mathbf {x} ,t),}$ ${\displaystyle u(x,t)}$ ${\displaystyle x}$ ${\displaystyle {\frac {\partial ^{2}u}{\partial t^{2}}}-c^{2}{\frac {\partial ^{2}u}{\partial x^{2}}}=0}$

La ecuación diferencial parcial vectorial anterior de segundo orden ofrece dos soluciones mutuamente independientes. Del término de velocidad cuadrática se puede ver que hay dos ondas que viajan en direcciones opuestas y que son posibles, de ahí la designación de “ecuación de onda bidireccional”. Se puede demostrar, para la propagación de ondas longitudinales planas, que la síntesis de dos ecuaciones de ondas unidireccionales conduce a una ecuación general de ondas bidireccionales. Para una ecuación especial de dos ondas con los resultados del operador d'Alembert: ^[8] ${\displaystyle c^{2}=(+c)^{2}=(-c)^{2}}$ ${\displaystyle +c}$ ${\displaystyle -c}$ ${\displaystyle \nabla \mathbf {c} =\mathbf {0} ,}$

$${\displaystyle \left({\frac {\partial }{\partial t}}-\mathbf {c} \cdot \nabla \right)\left({\frac {\partial }{\partial t}}+\mathbf {c} \cdot \nabla \right)\mathbf {u} =\left({\frac {\partial ^{2}}{\partial t^{2}}}+(\mathbf {c} \cdot \nabla )\mathbf {c} \cdot \nabla \right)\mathbf {u} =\left({\frac {\partial ^{2}}{\partial t^{2}}}+(\mathbf {c} \cdot \nabla )^{2}\right)\mathbf {u} =\mathbf {0} .}$$

${\displaystyle \nabla \mathbf {c} =\mathbf {0} ,}$

$${\displaystyle \left({\frac {\partial ^{2}}{\partial t^{2}}}+c^{2}\Delta \right)\mathbf {u} =\mathbf {0} .}$$

Por lo tanto, la ecuación de onda^[9] ${\displaystyle \mathbf {c} }$

$${\displaystyle {\frac {\partial \mathbf {u} }{\partial t}}-\mathbf {c} \cdot \nabla \mathbf {u} =\mathbf {0} .}$$

Ecuación de onda escalar en tres dimensiones espaciales.

El matemático y físico suizo Leonhard Euler (n. 1707) descubrió la ecuación de onda en tres dimensiones espaciales. ^[1]

Se puede obtener una solución del problema del valor inicial para la ecuación de onda en tres dimensiones espaciales a partir de la solución correspondiente para una onda esférica. El resultado también se puede utilizar para obtener la misma solución en dos dimensiones espaciales.

Ondas esféricas

La ecuación de onda se puede resolver utilizando la técnica de separación de variables . Para obtener una solución con frecuencias constantes, primero transformemos la ecuación de onda en el tiempo como

$${\displaystyle \Psi (\mathbf {r} ,t)=\int _{-\infty }^{\infty }\Psi (\mathbf {r} ,\omega )e^{-i\omega t}\,d\omega ,}$$

entonces obtenemos

$${\displaystyle \left(\nabla ^{2}+{\frac {\omega ^{2}}{c^{2}}}\right)\Psi (\mathbf {r} ,\omega )=0.}$$

Esta es la ecuación de Helmholtz y se puede resolver mediante separación de variables. Si se utilizan coordenadas esféricas para describir un problema, entonces la solución a la parte angular de la ecuación de Helmholtz viene dada por armónicos esféricos , y la ecuación radial ahora se convierte en ^[10]

$${\displaystyle \left[{\frac {d^{2}}{dr^{2}}}+{\frac {2}{r}}{\frac {d}{dr}}+k^{2}-{\frac {l(l+1)}{r^{2}}}\right]f_{l}(r)=0.}$$

Aquí k ≡ ω / c , y la solución completa ahora viene dada por

$${\displaystyle \Psi (\mathbf {r} ,\omega )=\sum _{lm}\left[A_{lm}^{(1)}h_{l}^{(1)}(kr)+A_{lm}^{(2)}h_{l}^{(2)}(kr)\right]Y_{lm}(\theta ,\phi ),}$$

H⁽¹⁾
_yo( kr )_⁽²⁾
_yo( kr )funciones esféricas de Hankel

Ejemplo

Para comprender mejor la naturaleza de estas ondas esféricas, retrocedamos y observemos el caso en el que l = 0 . En este caso, no hay dependencia angular y la amplitud depende sólo de la distancia radial, es decir, Ψ( r , t ) → u ( r , t ) . En este caso, la ecuación de onda se reduce a

$${\displaystyle \left(\nabla ^{2}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right)\Psi (\mathbf {r} ,t)=0,}$$

$${\displaystyle \left({\frac {\partial ^{2}}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial }{\partial r}}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right)u(r,t)=0.}$$

Esta ecuación se puede reescribir como

$${\displaystyle {\frac {\partial ^{2}(ru)}{\partial t^{2}}}-c^{2}{\frac {\partial ^{2}(ru)}{\partial r^{2}}}=0,}$$

ru

$${\displaystyle u(r,t)={\frac {1}{r}}F(r-ct)+{\frac {1}{r}}G(r+ct),}$$

FGfuente puntualr^{[ cita necesaria ]}

Para ver ejemplos físicos de soluciones a la ecuación de onda 3D que poseen dependencia angular, consulte radiación dipolar .

Onda esférica monocromática

Corte de frentes de onda esféricos, con una longitud de onda de 10 unidades, que se propagan desde una fuente puntual

Aunque la palabra "monocromático" no es exactamente exacta, ya que se refiere a luz o radiación electromagnética con frecuencia bien definida, el ánimo es descubrir el modo propio de la ecuación de onda en tres dimensiones. Siguiendo la derivación en la sección anterior sobre modos propios de onda plana, si nuevamente restringimos nuestras soluciones a ondas esféricas que oscilan en el tiempo con una frecuencia angular constante bien definida ω , entonces la función transformada ru ( r , t ) tiene simplemente onda plana soluciones:

$${\displaystyle ru(r,t)=Ae^{i(\omega t\pm kr)},}$$

$${\displaystyle u(r,t)={\frac {A}{r}}e^{i(\omega t\pm kr)}.}$$

De esto podemos observar que la intensidad máxima de la oscilación de onda esférica, caracterizada como la amplitud de onda cuadrada

$${\displaystyle I=|u(r,t)|^{2}={\frac {|A|^{2}}{r^{2}}},}$$

1/ r ²ley del cuadrado inverso

Solución de un problema general de valor inicial.

La ecuación de onda es lineal en u y no se modifica con las traslaciones en el espacio y el tiempo. Por tanto, podemos generar una gran variedad de soluciones traduciendo y sumando ondas esféricas. Sea φ ( ξ , η , ζ ) una función arbitraria de tres variables independientes, y sea la forma de onda esférica F una función delta : es decir, sea F un límite débil de funciones continuas cuya integral es la unidad, pero cuyo soporte (la región donde la función es distinta de cero) se reduce hasta el origen. Sea una familia de ondas esféricas con centro en ( ξ , η , ζ ) , y sea r la distancia radial desde ese punto. De este modo

$${\displaystyle r^{2}=(x-\xi )^{2}+(y-\eta )^{2}+(z-\zeta )^{2}.}$$

Si u es una superposición de tales ondas con función de ponderación φ , entonces

$${\displaystyle u(t,x,y,z)={\frac {1}{4\pi c}}\iiint \varphi (\xi ,\eta ,\zeta ){\frac {\delta (r-ct)}{r}}\,d\xi \,d\eta \,d\zeta ;}$$

4 πc

De la definición de la función delta, u también se puede escribir como

$${\displaystyle u(t,x,y,z)={\frac {t}{4\pi }}\iint _{S}\varphi (x+ct\alpha ,y+ct\beta ,z+ct\gamma )\,d\omega ,}$$

αβγSωS. u ( t , x )tφctx

$${\displaystyle u(t,x,y,z)=tM_{ct}[\phi ].}$$

Resulta que

$${\displaystyle u(0,x,y,z)=0,\quad u_{t}(0,x,y,z)=\phi (x,y,z).}$$

El valor medio es una función par de t y, por tanto, si

$${\displaystyle v(t,x,y,z)={\frac {\partial }{\partial t}}{\big (}tM_{ct}[\psi ]{\big )},}$$

$${\displaystyle v(0,x,y,z)=\psi (x,y,z),\quad v_{t}(0,x,y,z)=0.}$$

Estas fórmulas proporcionan la solución al problema del valor inicial de la ecuación de onda. Muestran que la solución en un punto dado P , dado ( t , x , y , z ) depende sólo de los datos de la esfera de radio ct que es intersectada por el cono de luz dibujado hacia atrás desde P. No depende de datos sobre el interior de esta esfera. Así, el interior de la esfera es una laguna para la solución. Este fenómeno se llama principio de Huygens . Esto es cierto para números impares de dimensión espacial, donde para una dimensión la integración se realiza sobre el límite de un intervalo con respecto a la medida de Dirac. No se satisface en dimensiones espaciales uniformes. El fenómeno de las lagunas ha sido ampliamente investigado en Atiyah , Bott y Gårding (1970, 1973).

Ecuación de onda escalar en dos dimensiones espaciales.

En dos dimensiones espaciales, la ecuación de onda es

$${\displaystyle u_{tt}=c^{2}\left(u_{xx}+u_{yy}\right).}$$

Podemos usar la teoría tridimensional para resolver este problema si consideramos u como una función en tres dimensiones que es independiente de la tercera dimensión. Si

$${\displaystyle u(0,x,y)=0,\quad u_{t}(0,x,y)=\phi (x,y),}$$

entonces la fórmula de la solución tridimensional se convierte en

$${\displaystyle u(t,x,y)=tM_{ct}[\phi ]={\frac {t}{4\pi }}\iint _{S}\phi (x+ct\alpha ,\,y+ct\beta )\,d\omega ,}$$

donde α y β son las dos primeras coordenadas de la esfera unitaria y d ω es el elemento de área de la esfera. Esta integral se puede reescribir como una integral doble sobre el disco D con centro ( x , y ) y radio ct :

$${\displaystyle u(t,x,y)={\frac {1}{2\pi c}}\iint _{D}{\frac {\phi (x+\xi ,y+\eta )}{\sqrt {(ct)^{2}-\xi ^{2}-\eta ^{2}}}}d\xi \,d\eta .}$$

Es evidente que la solución en ( t , x , y ) depende no sólo de los datos del cono de luz donde

$${\displaystyle (x-\xi )^{2}+(y-\eta )^{2}=c^{2}t^{2},}$$

Ecuación de onda escalar en dimensión general y fórmulas de Kirchhoff.

Queremos encontrar soluciones a u _tt − Δ u = 0 para u  : R ⁿ × (0, ∞) → R con u ( x , 0) = g ( x ) y u _t ( x , 0) = h ( x ) . Consulte Evans para obtener más detalles.

Dimensiones impares

Supongamos que n ≥ 3 es un número entero impar y g ∈ C ^{m +1} ( R ⁿ ) , h ∈ C ^m ( R ⁿ ) para m = ( n + 1)/2 . Sea γ _n = 1 × 3 × 5 × ⋯ × ( n − 2) y sea

$${\displaystyle u(x,t)={\frac {1}{\gamma _{n}}}\left[\partial _{t}\left({\frac {1}{t}}\partial _{t}\right)^{\frac {n-3}{2}}\left(t^{n-2}{\frac {1}{|\partial B_{t}(x)|}}\int _{\partial B_{t}(x)}g\,dS\right)+\left({\frac {1}{t}}\partial _{t}\right)^{\frac {n-3}{2}}\left(t^{n-2}{\frac {1}{|\partial B_{t}(x)|}}\int _{\partial B_{t}(x)}h\,dS\right)\right]}$$

Entonces

• ${\displaystyle u\in C^{2}{\big (}\mathbf {R} ^{n}\times [0,\infty ){\big )}}$,
• ${\displaystyle u_{tt}-\Delta u=0}$en , ${\displaystyle \mathbf {R} ^{n}\times (0,\infty )}$
• ${\displaystyle \lim _{(x,t)\to (x^{0},0)}u(x,t)=g(x^{0})}$,
• ${\displaystyle \lim _{(x,t)\to (x^{0},0)}u_{t}(x,t)=h(x^{0})}$.

Dimensiones pares

Supongamos que n ≥ 2 es un número entero par y g ∈ C ^{m +1} ( R ⁿ ) , h ∈ C ^m ( R ⁿ ) , para m = ( n + 2)/2 . Sea γ _n = 2 × 4 × ⋯ × n y sea

$${\displaystyle u(x,t)={\frac {1}{\gamma _{n}}}\left[\partial _{t}\left({\frac {1}{t}}\partial _{t}\right)^{\frac {n-2}{2}}\left(t^{n}{\frac {1}{|B_{t}(x)|}}\int _{B_{t}(x)}{\frac {g}{(t^{2}-|y-x|^{2})^{\frac {1}{2}}}}dy\right)+\left({\frac {1}{t}}\partial _{t}\right)^{\frac {n-2}{2}}\left(t^{n}{\frac {1}{|B_{t}(x)|}}\int _{B_{t}(x)}{\frac {h}{(t^{2}-|y-x|^{2})^{\frac {1}{2}}}}dy\right)\right]}$$

entonces

• tu ∈ C ² ( R ^norte × [0, ∞))
• tu _tt − Δ tu = 0 en R ^norte × (0, ∞)
• ${\displaystyle \lim _{(x,t)\to (x^{0},0)}u(x,t)=g(x^{0})}$
• ${\displaystyle \lim _{(x,t)\to (x^{0},0)}u_{t}(x,t)=h(x^{0})}$

Problemas con los límites

Una dimensión espacial

Reflexión y transmisión en la frontera de dos medios.

Para una onda incidente que viaja de un medio (donde la velocidad de la onda es c ₁ ) a otro medio (donde la velocidad de la onda es c ₂ ), una parte de la onda se transmitirá al segundo medio, mientras que otra parte se reflejará hacia el otro. dirección y permanece en el primer medio. La amplitud de la onda transmitida y la onda reflejada se puede calcular utilizando la condición de continuidad en el límite.

Considere la componente de la onda incidente con una frecuencia angular de ω , que tiene la forma de onda

$${\displaystyle u^{\text{inc}}(x,t)=Ae^{i(k_{1}x-\omega t)},\quad A\in \mathbb {C} .}$$

t = 0x = 0

$${\displaystyle u^{\text{refl}}(x,t)=Be^{i(-k_{1}x-\omega t)},\quad u^{\text{trans}}(x,t)=Ce^{i(k_{2}x-\omega t)},\quad B,C\in \mathbb {C} .}$$

$${\displaystyle u^{\text{inc}}(0,t)+u^{\text{refl}}(0,t)=u^{\text{trans}}(0,t),\quad u_{x}^{\text{inc}}(0,t)+u_{x}^{\text{ref}}(0,t)=u_{x}^{\text{trans}}(0,t).}$$

$${\displaystyle A+B=C,\quad A-B={\frac {k_{2}}{k_{1}}}C={\frac {c_{1}}{c_{2}}}C,}$$

$${\displaystyle {\frac {B}{A}}={\frac {c_{2}-c_{1}}{c_{2}+c_{1}}},\quad {\frac {C}{A}}={\frac {2c_{2}}{c_{2}+c_{1}}}.}$$

c ₂ < c ₁cambio de fase de reflexiónB / A < 0

$${\displaystyle {\frac {B^{2}}{c_{1}}}+{\frac {C^{2}}{c_{2}}}={\frac {A^{2}}{c_{1}}}.}$$

ω

El caso límite de c ₂ = 0 corresponde a un "extremo fijo" que no se mueve, mientras que el caso límite de c ₂ → ∞ corresponde a un "extremo libre".

La formulación de Sturm-Liouville

Una cuerda flexible que se estira entre dos puntos x = 0 y x = L satisface la ecuación de onda para t > 0 y 0 < x < L . En los puntos de frontera, u puede satisfacer una variedad de condiciones de frontera. Un formulario general que es apropiado para las solicitudes es

$${\displaystyle {\begin{aligned}-u_{x}(t,0)+au(t,0)&=0,\\u_{x}(t,L)+bu(t,L)&=0,\end{aligned}}}$$

donde a y b no son negativos. El caso en el que se requiere que u desaparezca en un punto final (es decir, "extremo fijo") es el límite de esta condición cuando los respectivos aob se acercan al infinito. El método de separación de variables consiste en buscar soluciones a este problema en la forma especial

$${\displaystyle u(t,x)=T(t)v(x).}$$

Una consecuencia es que

$${\displaystyle {\frac {T''}{c^{2}T}}={\frac {v''}{v}}=-\lambda .}$$

El valor propio λ debe determinarse de modo que haya una solución no trivial del problema de valores en la frontera

$${\displaystyle {\begin{aligned}v''+\lambda v=0,&\\-v'(0)+av(0)&=0,\\v'(L)+bv(L)&=0.\end{aligned}}}$$

Este es un caso especial del problema general de la teoría de Sturm-Liouville . Si a y b son positivos, los valores propios son todos positivos y las soluciones son funciones trigonométricas. Se puede obtener una solución que satisfaga las condiciones iniciales integrables al cuadrado para u y u _{t a partir de la expansión de estas funciones en la serie trigonométrica apropiada.}

Investigación por métodos numéricos.

Aproximando la cuerda continua con un número finito de puntos de masa equidistantes, se obtiene el siguiente modelo físico:

Tres puntos de masa consecutivos del modelo discreto para una cuerda

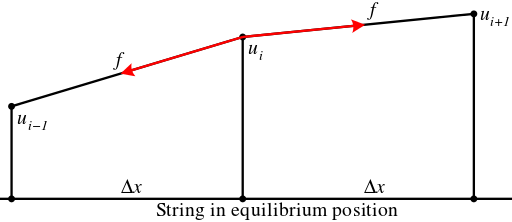
Si cada punto de masa tiene masa m , la tensión de la cuerda es f , la separación entre los puntos de masa es Δ x , y u _i , i = 1, ..., n son el desplazamiento de estos n puntos de su equilibrio puntos (es decir, su posición en una línea recta entre los dos puntos de unión de la cuerda), la componente vertical de la fuerza hacia el punto i + 1 es

y la componente vertical de la fuerza hacia el punto i − 1 es

Tomando la suma de estas dos fuerzas y dividiéndola por la masa m , se obtiene para el movimiento vertical:

Como la densidad de masa es

$${\displaystyle \rho ={\frac {m}{\Delta x}},}$$

La ecuación de onda se obtiene haciendo Δ x → 0 , en cuyo caso u _i ( t ) toma la forma u ( x , t ) , donde u ( x , t ) es una función continua de dos variables, ü _i toma la forma ∂ ² u /∂ t ² , y

$${\displaystyle {\frac {u_{i+1}+u_{i-1}-2u_{i}}{(\Delta x)^{2}}}\to {\frac {\partial ^{2}u}{\partial x^{2}}}.}$$

Pero la formulación discreta ( 3 ) de la ecuación de estado con un número finito de puntos de masa es la adecuada para una propagación numérica del movimiento de la cuerda. La condición límite

$${\displaystyle u(0,t)=u(L,t)=0,}$$

Lu ₁u _n

y

mientras que para 1 < i < n

donde c = √ f / ρ .

Si la cuerda se aproxima con 100 puntos de masa discretos, se obtienen 100 ecuaciones diferenciales de segundo orden acopladas ( 5 ), ( 6 ) y ( 7 ) o, equivalentemente, 200 ecuaciones diferenciales de primer orden acopladas.

Propagándolos hasta los tiempos.

$${\displaystyle {\frac {L}{c}}k(0.05),\ k=0,\dots ,5,}$$

Utilizando un método de varios pasos

La cuerda en 6 épocas consecutivas, la primera (roja) correspondiente al tiempo inicial con la cuerda en reposo

La curva roja es el estado inicial en el momento cero, en el que la cadena se "libera" en una forma predefinida ^[11] con todos . La curva azul es el estado en el momento, es decir, después de un tiempo que corresponde al tiempo que necesitaría una onda que se mueve con la velocidad de onda nominal c = √ f / ρ para un cuarto de la longitud de la cuerda. ${\displaystyle {\dot {u}}_{i}=0}$ ${\displaystyle {\tfrac {L}{c}}\cdot 0.25,}$

La forma de la cuerda en esos momentos. ${\displaystyle {\tfrac {L}{c}}k\cdot 0.05,\ k=6,\dots ,11}$

La onda viaja hacia la derecha con la velocidad c = √ f / ρ sin estar activamente limitada por las condiciones de contorno en los dos extremos de la cuerda. La forma de la onda es constante, es decir, la curva tiene la forma f ( x − ct ) .

La forma de la cuerda en esos momentos. ${\displaystyle {\tfrac {L}{c}}k\cdot 0.05,\ k=12,\dots ,17}$

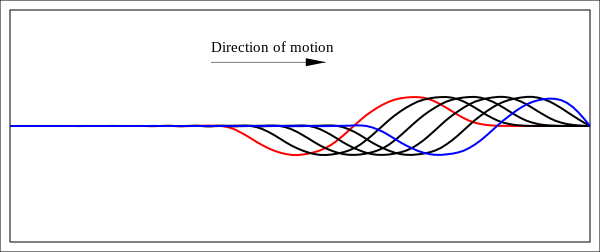
La restricción en el extremo derecho comienza a interferir con el movimiento, impidiendo que la onda levante el extremo de la cuerda.

La forma de la cuerda en esos momentos. ${\displaystyle {\tfrac {L}{c}}k\cdot 0.05,\ k=18,\dots ,23}$

La dirección del movimiento se invierte. Las curvas roja, verde y azul son los estados en los momentos , mientras que las 3 curvas negras corresponden a los estados en los que la onda comienza a moverse hacia la izquierda. ${\displaystyle {\tfrac {L}{c}}k\cdot 0.05,\ k=18,\dots ,20}$ ${\displaystyle k=21,\dots ,23}$

La forma de la cuerda en esos momentos. ${\displaystyle {\tfrac {L}{c}}k\cdot 0.05,\ k=24,\dots ,29}$

La forma de la cuerda en esos momentos. ${\displaystyle {\tfrac {L}{c}}k\cdot 0.05,\ k=30,\dots ,35}$

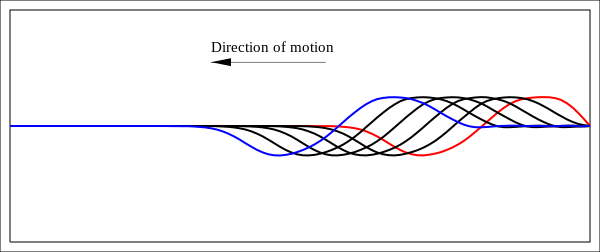
La onda ahora viaja hacia la izquierda y las restricciones en los puntos finales ya no están activas. Cuando finalmente se alcanza el otro extremo de la cuerda, la dirección se invertirá nuevamente de manera similar a lo que se muestra en la figura anterior para ${\displaystyle k=18,\dots ,23.}$

Varias dimensiones espaciales

Una solución de la ecuación de onda en dos dimensiones con una condición de frontera de desplazamiento cero a lo largo de todo el borde exterior.

La teoría del valor inicial unidimensional en la frontera puede extenderse a un número arbitrario de dimensiones espaciales. Considere un dominio D en un espacio x m ​​-dimensional , con límite B. Entonces la ecuación de onda debe satisfacerse si x está en D y t > 0 . En el límite de D , la solución u deberá satisfacer

$${\displaystyle {\frac {\partial u}{\partial n}}+au=0,}$$

donde n es la unidad normal hacia afuera a B y a es una función no negativa definida en B . El caso en el que u desaparece en B es un caso límite para un infinito que se acerca. Las condiciones iniciales son

$${\displaystyle u(0,x)=f(x),\quad u_{t}(0,x)=g(x),}$$

donde f y g están definidos en D . Este problema puede resolverse expandiendo f y g en las funciones propias del laplaciano en D , que satisfacen las condiciones de contorno. Por tanto, la función propia v satisface

$${\displaystyle \nabla \cdot \nabla v+\lambda v=0}$$

en D , y

$${\displaystyle {\frac {\partial v}{\partial n}}+av=0}$$

en B. _

En el caso de dos dimensiones espaciales, las funciones propias pueden interpretarse como los modos de vibración de un parche extendido sobre el límite B. Si B es un círculo, entonces estas funciones propias tienen una componente angular que es una función trigonométrica del ángulo polar θ , multiplicada por una función de Bessel (de orden entero) de la componente radial. Más detalles se encuentran en la ecuación de Helmholtz .

Si el límite es una esfera en tres dimensiones espaciales, las componentes angulares de las funciones propias son armónicos esféricos y las componentes radiales son funciones de Bessel de orden semientero.

Ecuación de onda no homogénea en una dimensión.

La ecuación de onda no homogénea en una dimensión es

$${\displaystyle u_{tt}(x,t)-c^{2}u_{xx}(x,t)=s(x,t)}$$

$${\displaystyle u(x,0)=f(x),}$$

$${\displaystyle u_{t}(x,0)=g(x).}$$

La función s ( x , t ) a menudo se denomina función fuente porque en la práctica describe los efectos de las fuentes de ondas sobre el medio que las transporta. Ejemplos físicos de funciones fuente incluyen la fuerza que impulsa una onda en una cuerda, o la carga o densidad de corriente en el calibre de Lorenz del electromagnetismo .

Un método para resolver el problema del valor inicial (con los valores iniciales como se plantearon anteriormente) es aprovechar una propiedad especial de la ecuación de onda en un número impar de dimensiones espaciales, a saber, que sus soluciones respetan la causalidad. Es decir, para cualquier punto ( x _i , t _i ) , el valor de u ( x _i , t _i ) depende sólo de los valores de f ( x _i + ct _i ) y f ( x _i − ct _i ) y del valores de la función g ( x ) entre ( xi − ct _{i )} y ( xi + _ct i ₎ . Esto se puede ver en la fórmula de d'Alembert , mencionada anteriormente, donde estas cantidades son las únicas que aparecen en ella. Físicamente, si la velocidad máxima de propagación es c , entonces ninguna parte de la onda que no pueda propagarse a un punto determinado en un tiempo determinado puede afectar la amplitud en el mismo punto y tiempo.

En términos de encontrar una solución, esta propiedad de causalidad significa que para cualquier punto dado de la línea que se está considerando, la única área que debe considerarse es el área que abarca todos los puntos que podrían afectar causalmente el punto que se está considerando. Denota el área que afecta causalmente _al punto ( xi _, ti ) como R _C. Supongamos que integramos la ecuación de onda no homogénea sobre esta región:

$${\displaystyle \iint _{R_{C}}{\big (}c^{2}u_{xx}(x,t)-u_{tt}(x,t){\big )}\,dx\,dt=\iint _{R_{C}}s(x,t)\,dx\,dt.}$$

Para simplificar esto enormemente, podemos usar el teorema de Green para simplificar el lado izquierdo y obtener lo siguiente:

$${\displaystyle \int _{L_{0}+L_{1}+L_{2}}{\big (}{-}c^{2}u_{x}(x,t)\,dt-u_{t}(x,t)\,dx{\big )}=\iint _{R_{C}}s(x,t)\,dx\,dt.}$$

El lado izquierdo es ahora la suma de tres integrales de línea a lo largo de los límites de la región de causalidad. Estos resultan ser bastante fáciles de calcular:

$${\displaystyle \int _{x_{i}-ct_{i}}^{x_{i}+ct_{i}}-u_{t}(x,0)\,dx=-\int _{x_{i}-ct_{i}}^{x_{i}+ct_{i}}g(x)\,dx.}$$

En lo anterior, el término a integrar con respecto al tiempo desaparece porque el intervalo de tiempo involucrado es cero, por lo tanto dt = 0 .

Para los otros dos lados de la región, vale la pena señalar que x ± ct es una constante, es decir, x _i ± ct _i , donde el signo se elige apropiadamente. Usando esto, podemos obtener la relación d x ± c d t = 0 , eligiendo nuevamente el signo correcto:

$${\displaystyle {\begin{aligned}\int _{L_{1}}{\big (}{-}c^{2}u_{x}(x,t)\,dt-u_{t}(x,t)\,dx{\big )}&=\int _{L_{1}}{\big (}cu_{x}(x,t)\,dx+cu_{t}(x,t)\,dt{\big )}\\&=c\int _{L_{1}}\,du(x,t)\\&=cu(x_{i},t_{i})-cf(x_{i}+ct_{i}).\end{aligned}}}$$

Y de manera similar para el segmento límite final:

$${\displaystyle {\begin{aligned}\int _{L_{2}}{\big (}{-}c^{2}u_{x}(x,t)\,dt-u_{t}(x,t)\,dx{\big )}&=-\int _{L_{2}}{\big (}cu_{x}(x,t)\,dx+cu_{t}(x,t)\,dt{\big )}\\&=-c\int _{L_{2}}\,du(x,t)\\&=cu(x_{i},t_{i})-cf(x_{i}-ct_{i}).\end{aligned}}}$$

Sumar los tres resultados y volver a colocarlos en la integral original da

$${\displaystyle {\begin{aligned}\iint _{R_{C}}s(x,t)\,dx\,dt&=-\int _{x_{i}-ct_{i}}^{x_{i}+ct_{i}}g(x)\,dx+cu(x_{i},t_{i})-cf(x_{i}+ct_{i})+cu(x_{i},t_{i})-cf(x_{i}-ct_{i})\\&=2cu(x_{i},t_{i})-cf(x_{i}+ct_{i})-cf(x_{i}-ct_{i})-\int _{x_{i}-ct_{i}}^{x_{i}+ct_{i}}g(x)\,dx.\end{aligned}}}$$

Resolviendo para u ( x _i , t _i ) , llegamos a

$${\displaystyle u(x_{i},t_{i})={\frac {f(x_{i}+ct_{i})+f(x_{i}-ct_{i})}{2}}+{\frac {1}{2c}}\int _{x_{i}-ct_{i}}^{x_{i}+ct_{i}}g(x)\,dx+{\frac {1}{2c}}\int _{0}^{t_{i}}\int _{x_{i}-c(t_{i}-t)}^{x_{i}+c(t_{i}-t)}s(x,t)\,dx\,dt.}$$

En la última ecuación de la secuencia, los límites de la integral sobre la función fuente se han hecho explícitos. Al observar esta solución, que es válida para todas las opciones ( x _i , t _i ) compatibles con la ecuación de onda, está claro que los dos primeros términos son simplemente la fórmula de d'Alembert, como se indicó anteriormente como la solución de la ecuación de onda homogénea. en una dimensión. La diferencia está en el tercer término, la integral sobre la fuente.

Ecuación de onda para medios no homogéneos, caso tridimensional.

Para la propagación de ondas unidireccionales, es decir, las ondas viajan en una dirección de onda predefinida ( o ) en medios no homogéneos, la propagación de ondas también se puede calcular con una ecuación de onda tensorial unidireccional (resultante de la factorización de la onda vectorial bidireccional). ecuación), y se puede derivar una solución analítica. ^[9] ${\displaystyle +c}$ ${\displaystyle -c}$

Otros sistemas de coordenadas

En tres dimensiones, la ecuación de onda, cuando se escribe en coordenadas cilíndricas elípticas , puede resolverse mediante la separación de variables, lo que conduce a la ecuación diferencial de Mathieu .

Más generalizaciones

ondas elásticas

La ecuación de onda elástica (también conocida como ecuación de Navier-Cauchy ) en tres dimensiones describe la propagación de ondas en un medio elástico homogéneo isotrópico . La mayoría de los materiales sólidos son elásticos, por lo que esta ecuación describe fenómenos como las ondas sísmicas en la Tierra y las ondas ultrasónicas utilizadas para detectar fallas en los materiales. Si bien es lineal, esta ecuación tiene una forma más compleja que las ecuaciones dadas anteriormente, ya que debe tener en cuenta tanto el movimiento longitudinal como el transversal:

$${\displaystyle \rho {\ddot {\mathbf {u} }}=\mathbf {f} +(\lambda +2\mu )\nabla (\nabla \cdot \mathbf {u} )-\mu \nabla \times (\nabla \times \mathbf {u} ),}$$

λ y μ son los llamados parámetros de Lamé que describen las propiedades elásticas del medio,

ρ es la densidad,

f es la función fuente (fuerza impulsora),

u es el vector de desplazamiento.

Usando ∇ × (∇ × u ) = ∇(∇ ⋅ u ) − ∇ ⋅ ∇ u = ∇(∇ ⋅ u ) − ∆ u , la ecuación de onda elástica se puede reescribir en la forma más común de la ecuación de Navier-Cauchy .

Tenga en cuenta que en la ecuación de onda elástica, tanto la fuerza como el desplazamiento son cantidades vectoriales . Por lo tanto, esta ecuación a veces se conoce como ecuación de onda vectorial. Como ayuda para la comprensión, el lector observará que si f y ∇ ⋅ u se establecen en cero, esto se convierte (efectivamente) en la ecuación de Maxwell para la propagación del campo eléctrico E , que solo tiene ondas transversales.

Relación de dispersión

En los fenómenos de ondas dispersivas , la velocidad de propagación de la onda varía con la longitud de onda de la onda, que se refleja mediante una relación de dispersión.

$${\displaystyle \omega =\omega (\mathbf {k} ),}$$

donde ω es la frecuencia angular y k es el vector de onda que describe soluciones de onda plana . Para las ondas de luz, la relación de dispersión es ω = ± c | k | , pero en general, la velocidad constante c se reemplaza por una velocidad de fase variable :

$${\displaystyle v_{\text{p}}={\frac {\omega (k)}{k}}.}$$

Ver también

• atenuación acústica
• Ecuación de onda acústica
• transformación de bateman
• Ecuación de ondas electromagnéticas
• ecuación de Helmholtz
• Ecuación de ondas electromagnéticas no homogéneas.
• operador de Laplace
• Matemáticas de la oscilación.
• ecuaciones de maxwell
• Ecuación de onda unidireccional
• ecuación de Schrödinger
• Onda estacionaria
• Vibraciones de una membrana circular.
• Teoría del absorbente de Wheeler-Feynman

Notas

1. Speiser, David. Descubriendo los principios de la mecánica 1600-1800 , p. 191 (Basilea: Birkhäuser, 2008).
2. Tipler, Paul y Mosca, Gene. Física para científicos e ingenieros, Volumen 1: Mecánica, oscilaciones y ondas; Termodinámica , págs. 470–471 (Macmillan, 2004).
3. Eric W. Weisstein . "La solución de d'Alembert". MundoMatemático . Consultado el 21 de enero de 2009 .
4. D'Alembert (1747) "Recherches sur la courbe que forme une corde tenduë mise en vibración" (Investigaciones sobre la curva que forma una cuerda tensa [cuando] se pone en vibración), Histoire de l'académie royale des sciences et belles lettres de Berlín , vol. 3, pág. 214–219.
   • Véase también: D'Alembert (1747) "Suite des recherches sur la courbe que forme une corde tenduë mise en vibración" (Más investigaciones sobre la curva que forma una cuerda tensa [cuando] se pone en vibración), Histoire de l'académie royale des sciences et belles lettres de Berlín , vol. 3, pág. 220–249.
   • Véase también: D'Alembert (1750) "Addition au mémoire sur la courbe que forme une corde tenduë mise en vibrator", Histoire de l'académie royale des sciences et belles lettres de Berlin , vol. 6, pág. 355–360.
5. "Ecuaciones de ondas lineales de primer y segundo orden" (PDF) . math.arizona.edu . Archivado desde el original (PDF) el 15 de diciembre de 2017.
6. V. Guruprasad (2015). "Evidencia de observación de modos de ondas viajeras que tienen cambios proporcionales a la distancia". EPL . 110 (5): 54001. arXiv : 1507.08222 . Código Bib : 2015EL....11054001G. doi :10.1209/0295-5075/110/54001. S2CID  42285652.
7. Bschorr, Oskar; Raida, Hans-Joachim (abril de 2021). "Ecuación de onda unidireccional esférica". Acústica . 3 (2): 309–315. doi : 10.3390/acústica3020021 . El texto se copió de esta fuente, que está disponible bajo una licencia internacional Creative Commons Attribution 4.0.
8. Raida, Hans-Joachim (octubre de 2022). "Operador de ondas unidireccionales". Acústica . 4 (4): 885–893. doi : 10.3390/acústica4040053 .
9. Bschorr, Oskar; Raida, Hans-Joachim (diciembre de 2021). "Ecuaciones de onda unidireccionales factorizadas". Acústica . 3 (4): 714–722. doi : 10.3390/acústica3040045 .
10. Jackson, John David (14 de agosto de 1998). Electrodinámica clásica (3ª ed.). Wiley. pag. 425.ISBN _ 978-0-471-30932-1.
11. El estado inicial de "Investigación por métodos numéricos" se establece con splines cuadráticos de la siguiente manera:

    ${\displaystyle u(0,x)=u_{0}\left(1-\left({\frac {x-x_{1}}{x_{1}}}\right)^{2}\right)}$para ${\displaystyle 0\leq x\leq x_{2},}$

    ${\displaystyle u(0,x)=u_{0}\left({\frac {x-x_{3}}{x_{1}}}\right)^{2}}$para ${\displaystyle x_{2}\leq x\leq x_{3},}$

    ${\displaystyle u(0,x)=0}$para ${\displaystyle x_{3}\leq x\leq L,}$

    con ${\displaystyle x_{1}={\tfrac {1}{10}}L,\ x_{2}=x_{1}+{\sqrt {\tfrac {1}{2}}}x_{1},\ x_{3}=x_{2}+{\sqrt {\tfrac {1}{2}}}x_{1}.}$

Referencias

• MF Atiyah, R. Bott, L. Garding, "Lacunas para operadores diferenciales hiperbólicos con coeficientes constantes I", Acta Mathematica , 124 (1970), 109–189.
• MF Atiyah, R. Bott y L. Garding, "Lacunas para operadores diferenciales hiperbólicos con coeficientes constantes II", Acta Mathematica , 131 (1973), 145-206.
• R. Courant, D. Hilbert, Métodos de física matemática, vol II . Interscience (Wiley) Nueva York, 1962.
• L. Evans, "Ecuaciones diferenciales parciales". Sociedad Estadounidense de Matemáticas Providence, 1998.
• "Ecuaciones de ondas lineales", EqWorld: El mundo de las ecuaciones matemáticas.
• "Ecuaciones de ondas no lineales", EqWorld: El mundo de las ecuaciones matemáticas.
• William C. Lane, "MISN-0-201 La ecuación de onda y sus soluciones", Proyecto PHYSNET .

enlaces externos

• Ecuaciones de ondas no lineales de Stephen Wolfram y Rob Knapp, Explorador de ecuaciones de ondas no lineales de Wolfram Demonstrations Project .
• Los aspectos matemáticos de las ecuaciones de onda se analizan en Dispersive PDE Wiki Archivado el 25 de abril de 2007 en Wayback Machine .
• Graham W. Griffiths y William E. Schiesser (2009). Ondas lineales y no lineales. Scholarpedia, 4(7):4308. doi:10.4249/scholarpedia.4308