
En física y matemáticas , la dimensión de un espacio (u objeto ) matemático se define informalmente como el número mínimo de coordenadas necesarias para especificar cualquier punto dentro de él. [1] [2] Por lo tanto, una línea tiene una dimensión de uno (1D) porque solo se necesita una coordenada para especificar un punto en ella, por ejemplo, el punto en 5 en una recta numérica. Una superficie , como el límite de un cilindro o una esfera , tiene una dimensión de dos (2D) porque se necesitan dos coordenadas para especificar un punto en ella; por ejemplo, se requieren tanto una latitud como una longitud para ubicar un punto en la superficie. de una esfera. Un espacio euclidiano bidimensional es un espacio bidimensional en el plano . El interior de un cubo , un cilindro o una esfera es tridimensional (3D) porque se necesitan tres coordenadas para localizar un punto dentro de estos espacios.
En la mecánica clásica , el espacio y el tiempo son categorías diferentes y se refieren al espacio y al tiempo absolutos . Esa concepción del mundo es un espacio de cuatro dimensiones pero no la que se consideró necesaria para describir el electromagnetismo . Las cuatro dimensiones (4D) del espacio-tiempo consisten en eventos que no están absolutamente definidos espacial y temporalmente, sino que se conocen en relación con el movimiento de un observador . El espacio de Minkowski se aproxima por primera vez al universo sin gravedad ; las variedades pseudo-riemannianas de la relatividad general describen el espacio-tiempo con materia y gravedad. Se utilizan 10 dimensiones para describir la teoría de supercuerdas (hiperespacio 6D + 4D), 11 dimensiones pueden describir la supergravedad y la teoría M (hiperespacio 7D + 4D), y el espacio de estados de la mecánica cuántica es un espacio funcional de dimensión infinita .
El concepto de dimensión no se limita a los objetos físicos.Los espacios de alta dimensión ocurren con frecuencia en matemáticas yciencias. Pueden serespacios euclidianosoespacios de parámetrosoespacios de configuracióncomo enlagrangianaohamiltoniana; estos sonespacios abstractos, independientes delespacio físico.
En matemáticas , la dimensión de un objeto es, a grandes rasgos, el número de grados de libertad de un punto que se mueve sobre ese objeto. En otras palabras, la dimensión es el número de parámetros o coordenadas independientes que se necesitan para definir la posición de un punto que está restringido a estar en el objeto. Por ejemplo, la dimensión de un punto es cero; la dimensión de una línea es uno, ya que un punto puede moverse en una línea sólo en una dirección (o en su contraria); la dimensión de un avión es dos, etc.
La dimensión es una propiedad intrínseca de un objeto, en el sentido de que es independiente de la dimensión del espacio en el que el objeto está o puede estar incrustado. Por ejemplo, una curva , como un círculo , es de dimensión uno, porque la posición de un punto en una curva está determinada por su distancia con signo a lo largo de la curva hasta un punto fijo en la curva. Esto es independiente del hecho de que una curva no puede incrustarse en un espacio euclidiano de dimensión inferior a dos, a menos que sea una línea.
La dimensión del espacio n euclidiano En es n . Al intentar generalizar a otros tipos de espacios, uno se enfrenta a la pregunta "¿qué hace que E n n sea dimensional?" Una respuesta es que para cubrir una bola fija en E n con bolas pequeñas de radio ε , se necesitan del orden de ε − n bolas pequeñas de este tipo. Esta observación lleva a la definición de la dimensión de Minkowski y su variante más sofisticada, la dimensión de Hausdorff , pero también hay otras respuestas a esa pregunta. Por ejemplo, el límite de una pelota en En se parece localmente a En -1 y esto lleva a la noción de dimensión inductiva . Si bien estas nociones concuerdan en En , resultan ser diferentes cuando se analizan espacios más generales .
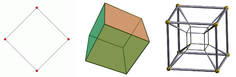
Un teseracto es un ejemplo de un objeto de cuatro dimensiones. Mientras que fuera de las matemáticas el uso del término "dimensión" es como en: "Un teseracto tiene cuatro dimensiones ", los matemáticos suelen expresarlo como: "El teseracto tiene dimensión 4 ", o: "La dimensión del teseracto es 4" o: 4D.
Aunque la noción de dimensiones superiores se remonta a René Descartes , el desarrollo sustancial de una geometría de dimensiones superiores no comenzó hasta el siglo XIX, a través del trabajo de Arthur Cayley , William Rowan Hamilton , Ludwig Schläfli y Bernhard Riemann . La Habilitationsschrift de Riemann de 1854 , la Theorie der vielfachen Kontinuität de Schläfli de 1852 y el descubrimiento de los cuaterniones por Hamilton y el descubrimiento de los octoniones por John T. Graves en 1843 marcaron el comienzo de la geometría de dimensiones superiores.
El resto de esta sección examina algunas de las definiciones matemáticas más importantes de dimensión.
La dimensión de un espacio vectorial es el número de vectores en cualquier base del espacio, es decir, el número de coordenadas necesarias para especificar cualquier vector. Esta noción de dimensión (la cardinalidad de una base) a menudo se denomina dimensión de Hamel o dimensión algebraica para distinguirla de otras nociones de dimensión.
Para el caso no libre , esto se generaliza a la noción de longitud de un módulo .
Se puede calcular la dimensión definida de forma única de cada variedad topológica conectada . Una variedad topológica conectada es localmente homeomorfa al espacio n euclidiano , en el que el número n es la dimensión de la variedad.
Para variedades diferenciables conectadas , la dimensión es también la dimensión del espacio vectorial tangente en cualquier punto.
En topología geométrica , la teoría de variedades se caracteriza por la forma en que las dimensiones 1 y 2 son relativamente elementales, los casos de alta dimensión n > 4 se simplifican al tener espacio adicional para "trabajar"; y los casos n = 3 y 4 son, en cierto sentido, los más difíciles. Este estado de cosas fue muy marcado en los diversos casos de la conjetura de Poincaré , en los que se aplican cuatro métodos de prueba diferentes.
La dimensión de una variedad depende del campo base con respecto al cual se define el espacio euclidiano. Si bien el análisis generalmente supone que una variedad está sobre los números reales , a veces es útil en el estudio de variedades complejas y variedades algebraicas trabajar sobre los números complejos . Un número complejo ( x + iy ) tiene una parte real x y una parte imaginaria y , en las que x e y son ambos números reales; por tanto, la dimensión compleja es la mitad de la dimensión real.
Por el contrario, en contextos algebraicamente no restringidos, se puede aplicar un único sistema de coordenadas complejo a un objeto que tiene dos dimensiones reales. Por ejemplo, una superficie esférica bidimensional ordinaria , cuando se le da una métrica compleja, se convierte en una esfera de Riemann de una dimensión compleja. [3]
La dimensión de una variedad algebraica se puede definir de varias formas equivalentes. La forma más intuitiva es probablemente la dimensión del espacio tangente en cualquier punto regular de una variedad algebraica . Otra forma intuitiva es definir la dimensión como el número de hiperplanos que se necesitan para tener una intersección con la variedad que se reduce a un número finito de puntos (dimensión cero). Esta definición se basa en el hecho de que la intersección de una variedad con un hiperplano reduce la dimensión en uno a menos que el hiperplano contenga la variedad.
Al ser un conjunto algebraico una unión finita de variedades algebraicas, su dimensión es el máximo de las dimensiones de sus componentes. Es igual a la longitud máxima de las cadenas de subvariedades del conjunto algebraico dado (la longitud de dicha cadena es el número de " ").
Cada variedad puede considerarse como una pila algebraica , y su dimensión como variedad concuerda con su dimensión como pila. Sin embargo, hay muchas pilas que no corresponden a variedades y algunas de ellas tienen una dimensión negativa. Específicamente, si V es una variedad de dimensión m y G es un grupo algebraico de dimensión n que actúa sobre V , entonces la pila de cocientes [ V / G ] tiene dimensión m − n . [4]
La dimensión de Krull de un anillo conmutativo es la longitud máxima de las cadenas de ideales primos que contiene, siendo una cadena de longitud n una secuencia de ideales primos relacionados por inclusión. Está fuertemente relacionado con la dimensión de una variedad algebraica, debido a la correspondencia natural entre las subvariedades y los ideales primos del anillo de los polinomios de la variedad.
Para un álgebra sobre un campo , la dimensión como espacio vectorial es finita si y sólo si su dimensión de Krull es 0.
Para cualquier espacio topológico normal X , la dimensión de cobertura de Lebesgue de X se define como el entero más pequeño n para el cual se cumple lo siguiente: cualquier cobertura abierta tiene un refinamiento abierto (una segunda cobertura abierta en la que cada elemento es un subconjunto de un elemento en la primera portada) de modo que ningún punto esté incluido en más de n + 1 elementos. En este caso tenue X = n . Para X una variedad, esto coincide con la dimensión mencionada anteriormente. Si no existe tal número entero n , entonces se dice que la dimensión de X es infinita y se escribe dim X = ∞ . Además, X tiene dimensión −1, es decir, tenue X = −1 si y sólo si X está vacío. Esta definición de dimensión de cobertura se puede extender desde la clase de espacios normales a todos los espacios de Tychonoff simplemente reemplazando el término "abierto" en la definición por el término " funcionalmente abierto ".
Una dimensión inductiva se puede definir inductivamente de la siguiente manera. Considere que un conjunto discreto de puntos (como una colección finita de puntos) tiene dimensión 0. Al arrastrar un objeto de dimensión 0 en alguna dirección, se obtiene un objeto de dimensión 0. Al arrastrar un objeto unidimensional en una nueva dirección , se obtiene un objeto bidimensional. En general, se obtiene un objeto de dimensión ( n + 1 ) arrastrando un objeto de dimensión n en una nueva dirección. La dimensión inductiva de un espacio topológico puede referirse a la dimensión inductiva pequeña o a la dimensión inductiva grande , y se basa en la analogía de que, en el caso de espacios métricos, las bolas ( n + 1 )-dimensionales tienen límites n -dimensionales , lo que permite una definición inductiva basada en la dimensión de los límites de conjuntos abiertos. Además, el límite de un conjunto discreto de puntos es el conjunto vacío y, por lo tanto, se puede considerar que el conjunto vacío tiene dimensión -1. [5]
De manera similar, para la clase de complejos CW , la dimensión de un objeto es la n más grande para la cual el n -esqueleto no es trivial. Intuitivamente, esto se puede describir de la siguiente manera: si el espacio original puede deformarse continuamente en una colección de triángulos de dimensiones superiores unidos en sus caras con una superficie complicada, entonces la dimensión del objeto es la dimensión de esos triángulos. [ cita necesaria ]
La dimensión de Hausdorff es útil para estudiar conjuntos estructuralmente complicados, especialmente fractales . La dimensión de Hausdorff está definida para todos los espacios métricos y, a diferencia de las dimensiones consideradas anteriormente, también puede tener valores reales no enteros. [6] La dimensión de la caja o dimensión de Minkowski es una variante de la misma idea. En general, existen más definiciones de dimensiones fractales que funcionan para conjuntos muy irregulares y alcanzan valores reales positivos no enteros.
Cada espacio de Hilbert admite una base ortonormal , y dos bases cualesquiera para un espacio particular tienen la misma cardinalidad . Esta cardinalidad se llama dimensión del espacio de Hilbert. Esta dimensión es finita si y sólo si la dimensión de Hamel del espacio es finita, y en este caso las dos dimensiones coinciden.
Las teorías de la física clásica describen tres dimensiones físicas : desde un punto particular en el espacio , las direcciones básicas en las que podemos movernos son arriba/abajo, izquierda/derecha y adelante/atrás. El movimiento en cualquier otra dirección puede expresarse únicamente en términos de estos tres. Bajar es lo mismo que subir una distancia negativa. Moverse en diagonal hacia arriba y hacia adelante es tal como lo implica el nombre de la dirección; es decir , moverse en una combinación lineal de arriba y adelante. En su forma más simple: una línea describe una dimensión, un plano describe dos dimensiones y un cubo describe tres dimensiones. (Ver Espacio y sistema de coordenadas cartesiano ).
Una dimensión temporal , o dimensión temporal , es una dimensión del tiempo. A menudo se hace referencia al tiempo como la " cuarta dimensión " por esta razón, pero eso no implica que sea una dimensión espacial [ cita necesaria ] . Una dimensión temporal es una forma de medir el cambio físico. Se percibe de manera diferente a las tres dimensiones espaciales en que solo hay una y que no podemos movernos libremente en el tiempo sino subjetivamente movernos en una dirección .
Las ecuaciones utilizadas en física para modelar la realidad no tratan el tiempo de la misma manera que los humanos comúnmente lo perciben. Las ecuaciones de la mecánica clásica son simétricas con respecto al tiempo , y las ecuaciones de la mecánica cuántica suelen ser simétricas si tanto el tiempo como otras cantidades (como la carga y la paridad ) se invierten. En estos modelos, la percepción del tiempo que fluye en una dirección es un artefacto de las leyes de la termodinámica (percibimos que el tiempo fluye en la dirección de una entropía creciente ).
El tratamiento más conocido del tiempo como dimensión es la relatividad especial de Poincaré y Einstein (y extendida a la relatividad general ), que trata el espacio y el tiempo percibidos como componentes de una variedad de cuatro dimensiones , conocida como espaciotiempo , y en el especial, Caso plano como espacio de Minkowski . El tiempo es diferente de otras dimensiones espaciales ya que el tiempo opera en todas las dimensiones espaciales. El tiempo opera en la primera, segunda y tercera dimensión, así como en las dimensiones espaciales teóricas, como por ejemplo en una cuarta dimensión espacial . Sin embargo, el tiempo no está presente en un solo punto de singularidad infinita absoluta tal como se define como un punto geométrico , ya que un punto infinitamente pequeño no puede tener cambios y, por lo tanto, no puede tener tiempo. Así como cuando un objeto se mueve a través de posiciones en el espacio, también se mueve a través de posiciones en el tiempo. En este sentido, la fuerza que mueve cualquier objeto a cambiar es el tiempo . [7] [8] [9]
En física, la norma aceptada es tres dimensiones de espacio y una de tiempo. Sin embargo, existen teorías que intentan unificar las cuatro fuerzas fundamentales introduciendo dimensiones adicionales / hiperespacio . En particular, la teoría de supercuerdas requiere 10 dimensiones de espacio-tiempo y se origina a partir de una teoría más fundamental de 11 dimensiones llamada tentativamente teoría M , que incluye cinco teorías de supercuerdas previamente distintas. La teoría de la supergravedad también promueve el espacio-tiempo 11D = hiperespacio 7D + 4 dimensiones comunes. Hasta la fecha, no se dispone de evidencia experimental u observacional directa que respalde la existencia de estas dimensiones adicionales. Si el hiperespacio existe, debe estar oculto para nosotros mediante algún mecanismo físico. Una posibilidad bien estudiada es que las dimensiones adicionales puedan "acurrucarse" a escalas tan pequeñas que sean efectivamente invisibles para los experimentos actuales.
En 1921, la teoría de Kaluza-Klein presentó la 5D incluyendo una dimensión extra del espacio. A nivel de la teoría cuántica de campos , la teoría de Kaluza-Klein unifica la gravedad con las interacciones de calibre , basándose en la comprensión de que la gravedad que se propaga en dimensiones adicionales pequeñas y compactas es equivalente a las interacciones de calibre a largas distancias. En particular, cuando la geometría de las dimensiones adicionales es trivial, reproduce el electromagnetismo . Sin embargo, a energías suficientemente altas o distancias cortas, esta configuración todavía sufre las mismas patologías que obstruyen los intentos directos de describir la gravedad cuántica . Por lo tanto, estos modelos todavía requieren una terminación UV , del tipo que la teoría de cuerdas pretende proporcionar. En particular, la teoría de supercuerdas requiere seis dimensiones compactas (hiperespacio 6D) que forman una variedad Calabi-Yau . Por tanto, la teoría de Kaluza-Klein puede considerarse como una descripción incompleta por sí sola o como un subconjunto de la construcción de modelos de la teoría de cuerdas.
Además de las dimensiones adicionales pequeñas y acurrucadas, puede haber dimensiones adicionales que no son evidentes porque la materia asociada con nuestro universo visible está localizada en un subespacio de (3 + 1) dimensiones . Por tanto, las dimensiones adicionales no tienen por qué ser pequeñas y compactas, sino que pueden ser dimensiones adicionales grandes . Las D-branas son objetos dinámicos extendidos de varias dimensionalidades predichos por la teoría de cuerdas que podrían desempeñar este papel. Tienen la propiedad de que las excitaciones de cuerdas abiertas, que están asociadas con interacciones de calibre, están confinadas a la brana por sus puntos finales, mientras que las cuerdas cerradas que median la interacción gravitacional son libres de propagarse por todo el espacio-tiempo, o "la masa". Esto podría estar relacionado con por qué la gravedad es exponencialmente más débil que las otras fuerzas, ya que efectivamente se diluye a medida que se propaga hacia un volumen de dimensiones superiores.
Algunos aspectos de la física de branas se han aplicado a la cosmología . Por ejemplo, la cosmología de los gases brana [10] [11] intenta explicar por qué hay tres dimensiones del espacio utilizando consideraciones topológicas y termodinámicas. Según esta idea, sería porque tres es el mayor número de dimensiones espaciales en las que las cuerdas pueden cruzarse genéricamente. Si inicialmente hay muchas vueltas de cuerdas alrededor de dimensiones compactas, el espacio sólo podría expandirse a tamaños macroscópicos una vez que se eliminen estas vueltas, lo que requiere cuerdas de vueltas opuestas para encontrarse y aniquilarse. Pero las cuerdas sólo pueden encontrarse entre sí para aniquilarse a un ritmo significativo en tres dimensiones, por lo que se deduce que sólo se permite que tres dimensiones del espacio crezcan dada esta clase de configuración inicial.
Se dice que las dimensiones adicionales son universales si todos los campos tienen la misma libertad para propagarse dentro de ellas.
Varios tipos de sistemas digitales se basan en el almacenamiento, análisis y visualización de formas geométricas, incluido el software de ilustración , el diseño asistido por computadora y los sistemas de información geográfica . Los diferentes sistemas vectoriales utilizan una amplia variedad de estructuras de datos para representar formas, pero casi todos se basan fundamentalmente en un conjunto de primitivas geométricas correspondientes a las dimensiones espaciales: [12]
Frecuentemente en estos sistemas, especialmente SIG y Cartografía , una representación de un fenómeno del mundo real puede tener una dimensión diferente (generalmente menor) que el fenómeno que se representa. Por ejemplo, una ciudad (una región bidimensional) puede representarse como un punto, o una carretera (un volumen tridimensional de material) puede representarse como una línea. Esta generalización dimensional se correlaciona con las tendencias en la cognición espacial. Por ejemplo, preguntar la distancia entre dos ciudades presupone un modelo conceptual de las ciudades como puntos, mientras que dar direcciones que impliquen viajar "arriba", "abajo" o "a lo largo" de una carretera implica un modelo conceptual unidimensional. Esto se hace frecuentemente con fines de eficiencia de datos, simplicidad visual o eficiencia cognitiva, y es aceptable si se entiende la distinción entre la representación y lo representado, pero puede causar confusión si los usuarios de la información asumen que la forma digital es una representación perfecta de la realidad. (es decir, creer que los caminos realmente son líneas).