Mecánica lagrangiana

Formulación de la mecánica clásica.

José Luis Lagrange (1736–1813)

En física , la mecánica lagrangiana es una formulación de la mecánica clásica basada en el principio de acción estacionaria (también conocido como principio de acción mínima). Fue introducido por el matemático y astrónomo italo-francés Joseph-Louis Lagrange en su presentación ante la Academia de Ciencias de Turín en 1760 ^[1] , que culminó en su gran obra de 1788, Mécanique analytique . ^[2]

La mecánica lagrangiana describe un sistema mecánico como un par ( M , L ) que consta de un espacio de configuración M y una función suave dentro de ese espacio llamada lagrangiana . Para muchos sistemas, L = T − V , donde T y V son la energía cinética y potencial del sistema, respectivamente. ^[3] ${\textstyle L}$

El principio de acción estacionaria requiere que la acción funcional del sistema derivada de L debe permanecer en un punto estacionario (un máximo , un mínimo o una silla ) durante toda la evolución temporal del sistema. Esta restricción permite el cálculo de las ecuaciones de movimiento del sistema utilizando las ecuaciones de Lagrange. ^[4]

Introducción

Cuenta obligada a moverse sobre un alambre sin fricción. El alambre ejerce una fuerza de reacción C sobre la cuenta para mantenerla sobre el alambre. La fuerza no restrictiva N en este caso es la gravedad. Observe que la posición inicial de la cuenta en el cable puede provocar diferentes movimientos.

Péndulo sencillo. Dado que la varilla es rígida, la posición de la masa está restringida según la ecuación f ( x , y ) = 0 , la fuerza de restricción C es la tensión en la varilla. Nuevamente, la fuerza no restrictiva N en este caso es la gravedad.

Supongamos que existe una cuenta que se desliza sobre un alambre o un péndulo simple que oscila . Si se sigue cada uno de los objetos masivos (cuenta, masa pendular) como una partícula, el cálculo del movimiento de la partícula usando la mecánica newtoniana requeriría resolver la fuerza restrictiva variable en el tiempo necesaria para mantener la partícula en el movimiento restringido (fuerza de reacción). ejercida por el alambre sobre la cuenta, o tensión en la varilla del péndulo). Para el mismo problema utilizando la mecánica lagrangiana, se observa la trayectoria que puede tomar la partícula y se elige un conjunto conveniente de coordenadas generalizadas independientes que caractericen completamente el posible movimiento de la partícula. Esta elección elimina la necesidad de que la fuerza de restricción entre en el sistema de ecuaciones resultante. Hay menos ecuaciones ya que no se calcula directamente la influencia de la restricción sobre la partícula en un momento dado.

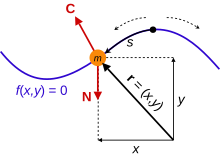
Para una amplia variedad de sistemas físicos, si el tamaño y la forma de un objeto masivo son insignificantes, es una simplificación útil tratarlo como una partícula puntual . Para un sistema de N partículas puntuales con masas m ₁ , m ₂ , ..., m _N , cada partícula tiene un vector de posición , denotado r ₁ , r ₂ , ..., r _N . Las coordenadas cartesianas suelen ser suficientes, por lo que r ₁ = ( x ₁ , y ₁ , z ₁ ) , r ₂ = ( x ₂ , y ₂ , z ₂ ) y así sucesivamente. En el espacio tridimensional , cada vector de posición requiere tres coordenadas para definir de forma única la ubicación de un punto, por lo que hay 3 N coordenadas para definir de forma única la configuración del sistema. Todos estos son puntos específicos en el espacio para localizar las partículas; un punto general en el espacio se escribe r = ( x , y , z ) . La velocidad de cada partícula es la rapidez con la que se mueve a lo largo de su trayectoria de movimiento y es la derivada temporal de su posición, por lo tanto

$${\displaystyle \mathbf {v} _{1}={\frac {d\mathbf {r} _{1}}{dt}},\mathbf {v} _{2}={\frac {d\mathbf {r} _{2}}{dt}},\ldots ,\mathbf {v} _{N}={\frac {d\mathbf {r} _{N}}{dt}}}$$

ecuaciones de movimientolas leyes de Newtonla fuerzala aceleración

$${\displaystyle \sum \mathbf {F} =m{\frac {d^{2}\mathbf {r} }{dt^{2}}}}$$

de NN ecuaciones diferenciales ordinarias

lagrangiano

En lugar de fuerzas, la mecánica lagrangiana utiliza las energías del sistema. La cantidad central de la mecánica lagrangiana es la lagrangiana , una función que resume la dinámica de todo el sistema. En general, el lagrangiano tiene unidades de energía, pero no una expresión única para todos los sistemas físicos. Cualquier función que genere las ecuaciones de movimiento correctas, de acuerdo con las leyes físicas, puede considerarse lagrangiana. Sin embargo, es posible construir expresiones generales para grandes clases de aplicaciones. El lagrangiano no relativista para un sistema de partículas en ausencia de un campo electromagnético viene dado por ^[5]

$${\displaystyle L=T-V}$$

$${\displaystyle T={\frac {1}{2}}\sum _{k=1}^{N}m_{k}v_{k}^{2}}$$

es la energía cinéticasuma^[6]Venergía potencial

La energía cinética es la energía del movimiento del sistema, y ​​v _k ² = v _k · v _k es la magnitud al cuadrado de la velocidad, equivalente al producto escalar de la velocidad consigo misma. La energía cinética es función únicamente de las velocidades v _k , no de las posiciones r _k ni del tiempo t , por lo que T = T ( v ₁ , v ₂ , ...) .

La energía potencial del sistema refleja la energía de interacción entre las partículas, es decir, cuánta energía tendrá cada partícula debido a todas las demás y otras influencias externas. Para fuerzas conservativas (por ejemplo, la gravedad newtoniana ), es función de los vectores de posición de las partículas únicamente, por lo que V = V ( r ₁ , r ₂ , ...) . Para aquellas fuerzas no conservativas que pueden derivarse de un potencial apropiado (por ejemplo, potencial electromagnético ), las velocidades aparecerán también, V = V ( r ₁ , r ₂ , ..., v ₁ , v ₂ , ...) . Si hay algún campo externo o fuerza impulsora externa que cambia con el tiempo, el potencial cambiará con el tiempo, por lo que generalmente V = V ( r ₁ , r ₂ , ..., v ₁ , v ₂ , ..., t ) .

La forma anterior de L no se cumple en la mecánica lagrangiana relativista o en presencia de un campo magnético cuando se usa la expresión típica para la energía potencial, y debe ser reemplazada por una función consistente con la relatividad especial o general. Además, para fuerzas disipativas (por ejemplo, fricción ) , se debe introducir otra función junto con L.

Una o más de las partículas pueden estar sujetas a una o más restricciones holonómicas ; dicha restricción se describe mediante una ecuación de la forma f ( r , t ) = 0 . Si el número de restricciones en el sistema es C , entonces cada restricción tiene una ecuación, f ₁ ( r , t ) = 0 , f ₂ ( r , t ) = 0 , ..., f _C ( r , t ) = 0 , cada uno de los cuales podría aplicarse a cualquiera de las partículas. Si la partícula k está sujeta a la restricción i , entonces f _i ( r _k , t ) = 0 . En cualquier instante de tiempo, las coordenadas de una partícula restringida están vinculadas entre sí y no son independientes. Las ecuaciones de restricción determinan los caminos permitidos por los que pueden moverse las partículas, pero no dónde están ni qué tan rápido van en cada instante de tiempo. Las restricciones no holonómicas dependen de las velocidades de las partículas, las aceleraciones o las derivadas de posición superiores. La mecánica lagrangiana sólo puede aplicarse a sistemas cuyas restricciones, si las hay, sean todas holonómicas . Tres ejemplos de restricciones no holonómicas son: ^[7] cuando las ecuaciones de restricción no son integrables, cuando las restricciones tienen desigualdades o con fuerzas complicadas no conservativas como la fricción. Las restricciones no holonómicas requieren un tratamiento especial y es posible que haya que volver a la mecánica newtoniana o utilizar otros métodos.

Si T o V o ambos dependen explícitamente del tiempo debido a restricciones que varían en el tiempo o influencias externas, el L lagrangiano ( r ₁ , r ₂ , ... v ₁ , v ₂ , ... t ) depende explícitamente del tiempo . Si ni la energía potencial ni la cinética dependen del tiempo, entonces el Lagrangiano L ( r ₁ , r ₂ ,... v ₁ , v ₂ ,...) es explícitamente independiente del tiempo . En cualquier caso, el lagrangiano siempre tendrá una dependencia temporal implícita a través de las coordenadas generalizadas.

Con estas definiciones, las ecuaciones de Lagrange del primer tipo son ^[8]

Ecuaciones de Lagrange  (primer tipo)

${\displaystyle {\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0}$

donde k = 1, 2, ..., N etiqueta las partículas, hay un multiplicador de Lagrange λ _i para cada ecuación de restricción f _i , y

$${\displaystyle {\frac {\partial }{\partial \mathbf {r} _{k}}}\equiv \left({\frac {\partial }{\partial x_{k}}},{\frac {\partial }{\partial y_{k}}},{\frac {\partial }{\partial z_{k}}}\right)\,,\quad {\frac {\partial }{\partial {\dot {\mathbf {r} }}_{k}}}\equiv \left({\frac {\partial }{\partial {\dot {x}}_{k}}},{\frac {\partial }{\partial {\dot {y}}_{k}}},{\frac {\partial }{\partial {\dot {z}}_{k}}}\right)}$$

derivadas parciales ∂/∂^{[nb 1]}derivada temporalN3 N + CNde C.

En el lagrangiano, las coordenadas de posición y los componentes de la velocidad son todas variables independientes , y las derivadas del lagrangiano se toman con respecto a éstas por separado de acuerdo con las reglas de diferenciación habituales (por ejemplo, la derivada parcial de L con respecto al componente de velocidad z de la partícula 2, definida por v _{z ,2} = dz ₂ / dt , es simplemente ∂ L /∂ v _{z ,2} ; no es necesario utilizar reglas de cadena incómodas ni derivadas totales para relacionar el componente de velocidad con la coordenada correspondiente z ₂ ).

En cada ecuación de restricción, una coordenada es redundante porque se determina a partir de las otras coordenadas. Por tanto, el número de coordenadas independientes es n = 3 N − C . Podemos transformar cada vector de posición en un conjunto común de n coordenadas generalizadas , convenientemente escritas como una n -tupla q = ( q ₁ , q ₂ , ... q _n ) , expresando cada vector de posición y, por tanto, las coordenadas de posición, como funciones de las coordenadas generalizadas y del tiempo,

$${\displaystyle \mathbf {r} _{k}=\mathbf {r} _{k}(\mathbf {q} ,t)=(x_{k}(\mathbf {q} ,t),y_{k}(\mathbf {q} ,t),z_{k}(\mathbf {q} ,t),t)\,.}$$

El vector q es un punto en el espacio de configuración del sistema. Las derivadas temporales de las coordenadas generalizadas se denominan velocidades generalizadas, y para cada partícula la transformación de su vector velocidad, la derivada total de su posición con respecto al tiempo, es

$${\displaystyle {\dot {q}}_{j}={\frac {\mathrm {d} q_{j}}{\mathrm {d} t}}\,,\quad \mathbf {v} _{k}=\sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}{\dot {q}}_{j}+{\frac {\partial \mathbf {r} _{k}}{\partial t}}\,.}$$

Dado esto v _k , la energía cinética en coordenadas generalizadas depende de las velocidades generalizadas, las coordenadas generalizadas y el tiempo si los vectores de posición dependen explícitamente del tiempo debido a restricciones que varían en el tiempo, entonces T = T ( q ,⋅q, t ) .

Con estas definiciones, las ecuaciones de Euler-Lagrange , o ecuaciones de Lagrange de segundo tipo ^{[9] [10]}

Ecuaciones de Lagrange  (segundo tipo)

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)={\frac {\partial L}{\partial q_{j}}}}$

Son resultados matemáticos del cálculo de variaciones , que también se pueden utilizar en mecánica. Sustituyendo en el lagrangiano L ( q , d q /d t , t ) , se obtienen las ecuaciones de movimiento del sistema. El número de ecuaciones ha disminuido en comparación con la mecánica newtoniana, de 3 N an = 3 N - C ecuaciones diferenciales de segundo orden acopladas en las coordenadas generalizadas. Estas ecuaciones no incluyen fuerzas restrictivas en absoluto, sólo se deben tener en cuenta las fuerzas no restrictivas.

Aunque las ecuaciones de movimiento incluyen derivadas parciales , los resultados de las derivadas parciales siguen siendo ecuaciones diferenciales ordinarias en las coordenadas de posición de las partículas. La derivada del tiempo total denotada d/d t a menudo implica una diferenciación implícita . Ambas ecuaciones son lineales en el lagrangiano, pero generalmente serán ecuaciones acopladas no lineales en las coordenadas.

De la mecánica newtoniana a la lagrangiana

las leyes de newton

Isaac Newton (1642-1727)

Para simplificar, las leyes de Newton se pueden ilustrar para una partícula sin mucha pérdida de generalidad (para un sistema de N partículas, todas estas ecuaciones se aplican a cada partícula del sistema). La ecuación de movimiento de una partícula de masa constante m es la segunda ley de Newton de 1687, en notación vectorial moderna.

$${\displaystyle \mathbf {F} =m\mathbf {a} \,,}$$

aFsobreecuaciones diferenciales ordinarias dertcondiciones inicialesrvt = 0

Las leyes de Newton son fáciles de usar en coordenadas cartesianas, pero las coordenadas cartesianas no siempre son convenientes y, para otros sistemas de coordenadas, las ecuaciones de movimiento pueden volverse complicadas. En un conjunto de coordenadas curvilíneas ξ = ( ξ ¹ , ξ ² , ξ ³ ) , la ley en notación de índice tensorial es la "forma lagrangiana" ^{[11] [12]}

$${\displaystyle F^{a}=m\left({\frac {\mathrm {d} ^{2}\xi ^{a}}{\mathrm {d} t^{2}}}+\Gamma ^{a}{}_{bc}{\frac {\mathrm {d} \xi ^{b}}{\mathrm {d} t}}{\frac {\mathrm {d} \xi ^{c}}{\mathrm {d} t}}\right)=g^{ak}\left({\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {\xi }}^{k}}}-{\frac {\partial T}{\partial \xi ^{k}}}\right)\,,\quad {\dot {\xi }}^{a}\equiv {\frac {\mathrm {d} \xi ^{a}}{\mathrm {d} t}}\,,}$$

F ^acomponente contravariante^a _bcsímbolos de Christoffel

$${\displaystyle T={\frac {1}{2}}mg_{bc}{\frac {\mathrm {d} \xi ^{b}}{\mathrm {d} t}}{\frac {\mathrm {d} \xi ^{c}}{\mathrm {d} t}}}$$

g _bccomponentes covariantestensor métricoabc

Puede parecer una complicación excesiva formular la ley de Newton de esta forma, pero tiene sus ventajas. Los componentes de la aceleración en términos de los símbolos de Christoffel se pueden evitar evaluando en su lugar las derivadas de la energía cinética. Si no hay ninguna fuerza resultante que actúe sobre la partícula, F = 0 , ésta no acelera, sino que se mueve con velocidad constante en línea recta. Matemáticamente, las soluciones de la ecuación diferencial son las geodésicas , las curvas de longitud extrema entre dos puntos en el espacio (éstas pueden terminar siendo mínimas por lo que son los caminos más cortos, pero eso no es necesario). En el espacio real plano 3D, las geodésicas son simplemente líneas rectas. Entonces, para una partícula libre, la segunda ley de Newton coincide con la ecuación geodésica y establece que las partículas libres siguen geodésicas, las trayectorias extremas por las que pueden moverse. Si la partícula está sujeta a fuerzas, F ≠ 0 , la partícula acelera debido a las fuerzas que actúan sobre ella y se desvía de las geodésicas que seguiría si estuviera libre. Con extensiones apropiadas de las cantidades dadas aquí en el espacio plano 3D al espaciotiempo curvo 4D , la forma anterior de la ley de Newton también se traslada a la relatividad general de Einstein , en cuyo caso las partículas libres siguen geodésicas en el espaciotiempo curvo que ya no son "líneas rectas". " en el sentido ordinario. ^[13]

Sin embargo, todavía necesitamos conocer la fuerza resultante total F que actúa sobre la partícula, lo que a su vez requiere la fuerza resultante no restrictiva N más la fuerza restrictiva resultante C.

$${\displaystyle \mathbf {F} =\mathbf {C} +\mathbf {N} \,.}$$

Las fuerzas de restricción pueden resultar complicadas, ya que generalmente dependerán del tiempo. Además, si hay restricciones, las coordenadas curvilíneas no son independientes sino que están relacionadas por una o más ecuaciones de restricción.

Las fuerzas restrictivas pueden eliminarse de las ecuaciones de movimiento de modo que solo queden las fuerzas no restrictivas, o incluirse incluyendo las ecuaciones restrictivas en las ecuaciones de movimiento.

El principio de D'Alembert

Juan de Alembert (1717—1783)

Fuerza de restricción C y desplazamiento virtual δ r para una partícula de masa m confinada a una curva. La fuerza resultante sin restricción es N.

Un resultado fundamental en la mecánica analítica es el principio de D'Alembert , introducido en 1708 por Jacques Bernoulli para comprender el equilibrio estático , y desarrollado por D'Alembert en 1743 para resolver problemas dinámicos. ^[14] El principio afirma que para N partículas el trabajo virtual, es decir, el trabajo a lo largo de un desplazamiento virtual, δ r _k , es cero: ^[6]

$${\displaystyle \sum _{k=1}^{N}(\mathbf {N} _{k}+\mathbf {C} _{k}-m_{k}\mathbf {a} _{k})\cdot \delta \mathbf {r} _{k}=0\,.}$$

Los desplazamientos virtuales , δ r _k , son por definición cambios infinitesimales en la configuración del sistema consistentes con las fuerzas restrictivas que actúan sobre el sistema en un instante de tiempo , ^[15] es decir, de tal manera que las fuerzas restrictivas mantienen el movimiento restringido. . No son lo mismo que los desplazamientos reales en el sistema, que son causados ​​por las fuerzas resultantes, restrictivas y no restrictivas, que actúan sobre la partícula para acelerarla y moverla. ^{[nb 2]} El trabajo virtual es el trabajo realizado a lo largo de un desplazamiento virtual para cualquier fuerza (con o sin restricción).

Dado que las fuerzas restrictivas actúan perpendicularmente al movimiento de cada partícula en el sistema para mantener las restricciones, el trabajo virtual total de las fuerzas restrictivas que actúan sobre el sistema es cero: ^{[16] [nb 3]}

$${\displaystyle \sum _{k=1}^{N}\mathbf {C} _{k}\cdot \delta \mathbf {r} _{k}=0\,,}$$

$${\displaystyle \sum _{k=1}^{N}(\mathbf {N} _{k}-m_{k}\mathbf {a} _{k})\cdot \delta \mathbf {r} _{k}=0\,.}$$

Así, el principio de D'Alembert nos permite concentrarnos sólo en las fuerzas aplicadas no restrictivas y excluir las fuerzas restrictivas en las ecuaciones de movimiento. ^{[17] [18]} La forma mostrada también es independiente de la elección de las coordenadas. Sin embargo, no se puede utilizar fácilmente para establecer las ecuaciones de movimiento en un sistema de coordenadas arbitrario, ya que los desplazamientos δ r _k podrían estar conectados por una ecuación de restricción, lo que nos impide establecer los N sumandos individuales en 0. Por lo tanto, buscaremos una sistema de coordenadas mutuamente independientes para el cual la suma total será 0 si y solo si los sumandos individuales son 0. Establecer cada uno de los sumandos en 0 eventualmente nos dará nuestras ecuaciones de movimiento separadas.

Ecuaciones de movimiento según el principio de D'Alembert

Si hay restricciones sobre la partícula k , entonces dado que las coordenadas de la posición r _k = ( x _k , y _k , z _k ) están unidas por una ecuación de restricción, también lo están las de los desplazamientos virtuales δ r _k = ( δx _k , δyk , δzk ) . _{_ _} Dado que las coordenadas generalizadas son independientes, podemos evitar las complicaciones con δ r _k convirtiendo a desplazamientos virtuales en las coordenadas generalizadas. Estos están relacionados de la misma forma que un diferencial total , ^[6]

$${\displaystyle \delta \mathbf {r} _{k}=\sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\delta q_{j}\,.}$$

No existe una derivada temporal parcial con respecto al tiempo multiplicado por un incremento de tiempo, ya que se trata de un desplazamiento virtual, uno a lo largo de las restricciones en un instante de tiempo.

El primer término en el principio de D'Alembert anterior es el trabajo virtual realizado por las fuerzas no restrictivas N _k a lo largo de los desplazamientos virtuales δ r _k , y puede convertirse sin pérdida de generalidad en análogos generalizados mediante la definición de fuerzas generalizadas.

$${\displaystyle Q_{j}=\sum _{k=1}^{N}\mathbf {N} _{k}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\,,}$$

$${\displaystyle \sum _{k=1}^{N}\mathbf {N} _{k}\cdot \delta \mathbf {r} _{k}=\sum _{k=1}^{N}\mathbf {N} _{k}\cdot \sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\delta q_{j}=\sum _{j=1}^{n}Q_{j}\delta q_{j}\,.}$$

Esta es la mitad de la conversión a coordenadas generalizadas. Queda por convertir el término de aceleración en coordenadas generalizadas, lo cual no es inmediatamente obvio. Recordando la forma de Lagrange de la segunda ley de Newton, se pueden encontrar las derivadas parciales de la energía cinética con respecto a las coordenadas y velocidades generalizadas para dar el resultado deseado: ^[6]

$${\displaystyle \sum _{k=1}^{N}m_{k}\mathbf {a} _{k}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}\,.}$$

Ahora el principio de D'Alembert está en las coordenadas generalizadas según sea necesario,

$${\displaystyle \sum _{j=1}^{n}\left[Q_{j}-\left({\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}\right)\right]\delta q_{j}=0\,,}$$

δq _jlas ecuaciones de Lagrange ^{[19] [20]}ecuaciones generalizadas de movimiento^[21]

$${\displaystyle Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}}$$

Estas ecuaciones son equivalentes a las leyes de Newton para las fuerzas sin restricciones . Las fuerzas generalizadas en esta ecuación se derivan únicamente de las fuerzas no restrictivas; las fuerzas restrictivas han sido excluidas del principio de D'Alembert y no es necesario encontrarlas. Las fuerzas generalizadas pueden ser no conservadoras, siempre que satisfagan el principio de D'Alembert. ^[22]

Ecuaciones de Euler-Lagrange y principio de Hamilton

A medida que el sistema evoluciona, q traza un camino a través del espacio de configuración (sólo se muestran algunas). El camino tomado por el sistema (rojo) tiene una acción estacionaria (δ S = 0) ante pequeños cambios en la configuración del sistema (δ q ). ^[23]

Para una fuerza no conservativa que depende de la velocidad, es posible encontrar una función de energía potencial V que dependa de las posiciones y velocidades. Si las fuerzas generalizadas Q _i pueden derivarse de un potencial V tal que ^{[24] [25]}

$${\displaystyle Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial V}{\partial {\dot {q}}_{j}}}-{\frac {\partial V}{\partial q_{j}}}\,,}$$

L = T − Vlas ecuaciones de Lagrange de segundo tipode Euler-Lagrange

$${\displaystyle {\frac {\partial L}{\partial q_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}=0\,.}$$

Sin embargo, las ecuaciones de Euler-Lagrange sólo pueden explicar fuerzas no conservativas si se puede encontrar un potencial como se muestra. Puede que esto no siempre sea posible para fuerzas no conservativas, y las ecuaciones de Lagrange no implican ningún potencial, sólo fuerzas generalizadas; por tanto, son más generales que las ecuaciones de Euler-Lagrange.

Las ecuaciones de Euler-Lagrange también se derivan del cálculo de variaciones . La variación del lagrangiano es

$${\displaystyle \delta L=\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}\delta q_{j}+{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta {\dot {q}}_{j}\right)\,,\quad \delta {\dot {q}}_{j}\equiv \delta {\frac {\mathrm {d} q_{j}}{\mathrm {d} t}}\equiv {\frac {\mathrm {d} (\delta q_{j})}{\mathrm {d} t}}\,,}$$

diferencial totalLintegración por partesδq _jLq _jtδq _jtδq _j

$${\displaystyle \int _{t_{1}}^{t_{2}}\delta L\,\mathrm {d} t=\int _{t_{1}}^{t_{2}}\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}\delta q_{j}+{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right)-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right)\,\mathrm {d} t\,=\sum _{j=1}^{n}\left[{\frac {\partial L}{\partial {\dot {q}}_{j}}}\delta q_{j}\right]_{t_{1}}^{t_{2}}+\int _{t_{1}}^{t_{2}}\sum _{j=1}^{n}\left({\frac {\partial L}{\partial q_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)\delta q_{j}\,\mathrm {d} t\,.}$$

Ahora bien, si la condición δq _j ( t ₁ ) = δq _j ( t ₂ ) = 0 se cumple para todo j , los términos no integrados son cero. Si además toda la integral de tiempo de δL es cero, entonces debido a que los δq _j son independientes, y la única manera de que una integral definida sea cero es si el integrando es igual a cero, cada uno de los coeficientes de δq _j también debe ser cero. Luego obtenemos las ecuaciones de movimiento. Esto se puede resumir en el principio de Hamilton :

$${\displaystyle \int _{t_{1}}^{t_{2}}\delta L\,\mathrm {d} t=0\,.}$$

La integral de tiempo del lagrangiano es otra cantidad llamada acción , definida como ^[26]

$${\displaystyle S=\int _{t_{1}}^{t_{2}}L\,\mathrm {d} t\,,}$$

funcionalt ₁t ₂momento angular

$${\displaystyle \delta S=0\,.}$$

Por lo tanto, en lugar de pensar en partículas que se aceleran en respuesta a fuerzas aplicadas, se podría pensar en ellas seleccionando el camino con una acción estacionaria, con los puntos finales del camino en el espacio de configuración mantenidos fijos en los tiempos inicial y final. El principio de Hamilton a veces se denomina principio de acción mínima ; sin embargo, la acción funcional solo necesita ser estacionaria , no necesariamente un valor máximo o mínimo. Cualquier variación del funcional da un aumento en la integral funcional de la acción.

Históricamente, la idea de encontrar el camino más corto que puede seguir una partícula sometida a una fuerza motivó las primeras aplicaciones del cálculo de variaciones a problemas mecánicos, como el problema de la Braquistocrona resuelto por Jean Bernoulli en 1696, así como por Leibniz , Daniel Bernoulli , L'Hôpital por la misma época y Newton al año siguiente. ^[27] El propio Newton estaba pensando en la línea del cálculo variacional, pero no lo publicó. ^[27] Estas ideas, a su vez, conducen a los principios variacionales de la mecánica, de Fermat , Maupertuis , Euler , Hamilton y otros.

El principio de Hamilton se puede aplicar a restricciones no holonómicas si las ecuaciones de restricción se pueden expresar en una determinada forma, una combinación lineal de diferenciales de primer orden en las coordenadas. La ecuación de restricción resultante se puede reorganizar en una ecuación diferencial de primer orden. ^[28] Esto no se dará aquí.

Multiplicadores y restricciones de Lagrange

La L lagrangiana se puede variar en las coordenadas cartesianas r _k , para N partículas,

$${\displaystyle \int _{t_{1}}^{t_{2}}\sum _{k=1}^{N}\left({\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}\right)\cdot \delta \mathbf {r} _{k}\,\mathrm {d} t=0\,.}$$

El principio de Hamilton sigue siendo válido incluso si las coordenadas en las que se expresa L no son independientes, aquí r _k , pero aún se supone que las restricciones son holonómicas. ^[29] Como siempre, los puntos finales son fijos δ r _k ( t ₁ ) = δ r _k ( t ₂ ) = 0 para todo k . Lo que no se puede hacer es simplemente igualar los coeficientes de δ r _k a cero porque los δ r _k no son independientes. En cambio, se puede utilizar el método de los multiplicadores de Lagrange para incluir las restricciones. Multiplicando cada ecuación de restricción f _i ( r _k , t ) = 0 por un multiplicador de Lagrange λ _i para i = 1, 2, ..., C y sumando los resultados al lagrangiano original, se obtiene el nuevo lagrangiano

$${\displaystyle L'=L(\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,{\dot {\mathbf {r} }}_{1},{\dot {\mathbf {r} }}_{2},\ldots ,t)+\sum _{i=1}^{C}\lambda _{i}(t)f_{i}(\mathbf {r} _{k},t)\,.}$$

Los multiplicadores de Lagrange son funciones arbitrarias del tiempo t , pero no funciones de las coordenadas r _k , por lo que los multiplicadores están en pie de igualdad con las coordenadas de posición. Variar este nuevo Lagrangiano e integrarlo con respecto al tiempo da

$${\displaystyle \int _{t_{1}}^{t_{2}}\delta L'\mathrm {d} t=\int _{t_{1}}^{t_{2}}\sum _{k=1}^{N}\left({\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}\right)\cdot \delta \mathbf {r} _{k}\,\mathrm {d} t=0\,.}$$

Los multiplicadores introducidos se pueden encontrar de modo que los coeficientes de δ r _k sean cero, aunque los r _k no sean independientes. A continuación se presentan las ecuaciones de movimiento. Del análisis anterior, obtener la solución de esta integral es equivalente al enunciado

$${\displaystyle {\frac {\partial L'}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {\mathbf {r} }}_{k}}}=0\quad \Rightarrow \quad {\frac {\partial L}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {\mathbf {r} }}_{k}}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0\,,}$$

las ecuaciones de Lagrange de primer tipoλ _i

$${\displaystyle {\frac {\partial L'}{\partial \lambda _{i}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {\lambda }}_{i}}}=0\quad \Rightarrow \quad f_{i}(\mathbf {r} _{k},t)=0\,.}$$

Para el caso de una fuerza conservativa dada por el gradiente de alguna energía potencial V , una función de las _coordenadas rk únicamente, sustituyendo el lagrangiano L = T − V se obtiene

$${\displaystyle \underbrace {{\frac {\partial T}{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {\mathbf {r} }}_{k}}}} _{-\mathbf {F} _{k}}+\underbrace {-{\frac {\partial V}{\partial \mathbf {r} _{k}}}} _{\mathbf {N} _{k}}+\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}=0\,,}$$

e identificando las derivadas de la energía cinética como la (negativa de) la fuerza resultante, y las derivadas del potencial igualando la fuerza sin restricción, se deduce que las fuerzas con restricción son

$${\displaystyle \mathbf {C} _{k}=\sum _{i=1}^{C}\lambda _{i}{\frac {\partial f_{i}}{\partial \mathbf {r} _{k}}}\,,}$$

Propiedades del lagrangiano

No unicidad

El Lagrangiano de un sistema dado no es único. Un L lagrangiano puede multiplicarse por una constante a distinta de cero y desplazarse por una constante b arbitraria , y el nuevo L ′ = aL + b describirá el mismo movimiento que L. Si uno se restringe como arriba a trayectorias q sobre un intervalo de tiempo dado [ t _st , t _fin ] } y puntos finales fijos P _st = q ( t _st ) y P _fin = q ( t _fin ) , entonces dos lagrangianos describen el mismo sistema puede diferir por la "derivada del tiempo total" de una función f ( q , t ) : ^[30]

${\displaystyle L'(\mathbf {q} ,{\dot {\mathbf {q} }},t)=L(\mathbf {q} ,{\dot {\mathbf {q} }},t)+{\frac {\mathrm {d} f(\mathbf {q} ,t)}{\mathrm {d} t}},}$

donde significa ${\displaystyle \textstyle {\frac {\mathrm {d} f(\mathbf {q} ,t)}{\mathrm {d} t}}}$ ${\displaystyle \textstyle {\frac {\partial f(\mathbf {q} ,t)}{\partial t}}+\sum _{i}{\frac {\partial f(\mathbf {q} ,t)}{\partial q_{i}}}{\dot {q}}_{i}.}$

Ambos lagrangianos L y L ′ producen las mismas ecuaciones de movimiento ^{[31] [32]} ya que las acciones correspondientes S y S ′ están relacionadas a través de

${\displaystyle {\begin{aligned}S'[\mathbf {q} ]=\int \limits _{t_{\text{st}}}^{t_{\text{fin}}}L'(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt=\int \limits _{t_{\text{st}}}^{t_{\text{fin}}}L(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)\,dt+\int _{t_{\text{st}}}^{t_{\text{fin}}}{\frac {\mathrm {d} f(\mathbf {q} (t),t)}{\mathrm {d} t}}\,dt\\=S[\mathbf {q} ]+f(P_{\text{fin}},t_{\text{fin}})-f(P_{\text{st}},t_{\text{st}}),\end{aligned}}}$

con los dos últimos componentes f ( P _fin , t _fin ) y f ( P _st , t _st ) independientes de q .

Invariancia bajo transformaciones puntuales.

Dado un conjunto de coordenadas generalizadas q , si cambiamos estas variables a un nuevo conjunto de coordenadas generalizadas Q según una transformación puntual Q = Q ( q , t ) que es invertible como q = q ( Q , t ) , el nuevo lagrangiano L ′ es función de las nuevas coordenadas

${\displaystyle L'(\mathbf {Q} ,{\dot {\mathbf {Q} }},t)=L(\mathbf {q} (\mathbf {Q} ,t),{\dot {\mathbf {q} }}(\mathbf {Q} ,{\dot {\mathbf {Q} }},t),t)\,,}$

y según la regla de la cadena para la diferenciación parcial, las ecuaciones de Lagrange son invariantes bajo esta transformación; ^[33]

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L'}{\partial {\dot {Q}}_{i}}}={\frac {\partial L'}{\partial Q_{i}}}\,.}$

Esto puede simplificar las ecuaciones de movimiento.

Coordenadas cíclicas y momentos conservados.

Una propiedad importante del lagrangiano es que a partir de él se pueden leer fácilmente cantidades conservadas . El impulso generalizado "canónicamente conjugado con" la coordenada q _i se define por

${\displaystyle p_{i}={\frac {\partial L}{\partial {\dot {q}}_{i}}}.}$

Si la L lagrangiana no depende de alguna coordenada q _i , se deduce inmediatamente de las ecuaciones de Euler-Lagrange que

${\displaystyle {\dot {p}}_{i}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}={\frac {\partial L}{\partial q_{i}}}=0}$

y la integración muestra que el momento generalizado correspondiente es igual a una cantidad constante y conservada. Este es un caso especial del teorema de Noether . Estas coordenadas se denominan "cíclicas" o "ignorables".

Por ejemplo, un sistema puede tener un lagrangiano

${\displaystyle L(r,\theta ,{\dot {s}},{\dot {z}},{\dot {r}},{\dot {\theta }},{\dot {\phi }},t)\,,}$

donde r y z son longitudes a lo largo de líneas rectas, s es la longitud de un arco a lo largo de alguna curva y θ y φ son ángulos. Observe que z , s y φ están ausentes en el lagrangiano aunque sus velocidades no lo estén. Entonces el momento

${\displaystyle p_{z}={\frac {\partial L}{\partial {\dot {z}}}}\,,\quad p_{s}={\frac {\partial L}{\partial {\dot {s}}}}\,,\quad p_{\phi }={\frac {\partial L}{\partial {\dot {\phi }}}}\,,}$

son todas cantidades conservadas. Las unidades y naturaleza de cada impulso generalizado dependerán de la coordenada correspondiente; en este caso p _z es un momento de traslación en la dirección z , p _s también es un momento de traslación a lo largo de la curva s medida, y p _φ es un momento angular en el plano en el que se mide el ángulo φ . Por complicado que sea el movimiento de Como está el sistema, todas las coordenadas y velocidades variarán de tal manera que estos momentos se conserven.

Energía

Dado un lagrangiano, el hamiltoniano del sistema mecánico correspondiente es, por definición, ${\displaystyle L,}$

${\displaystyle H={\biggl (}\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}{\biggr )}-L.}$

Esta cantidad será equivalente a energía si las coordenadas generalizadas son coordenadas naturales, es decir. no tienen una dependencia temporal explícita al expresar el vector de posición: . De: ${\displaystyle {\vec {r}}={\vec {r}}(q_{1},\cdots ,q_{n})}$

${\displaystyle T={\frac {m}{2}}v^{2}={\frac {m}{2}}\sum _{i,j}\left({\frac {\partial {\vec {r}}}{\partial q_{i}}}{\dot {q}}_{i}\right)\cdot \left({\frac {\partial {\vec {r}}}{\partial q_{j}}}{\dot {q}}_{j}\right)={\frac {m}{2}}\sum _{i,j}a_{ij}{\dot {q}}_{i}{\dot {q}}_{j}}$

${\displaystyle \sum _{k=1}^{n}{\dot {q}}_{k}{\frac {\partial T}{\partial {\dot {q}}_{k}}}={\frac {m}{2}}\left(2\sum _{i,j}a_{ij}{\dot {q}}_{i}{\dot {q}}_{j}\right)=2T}$

${\displaystyle H={\biggl (}\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}{\biggr )}-L=2T-(T-V)=T+V=E}$

donde es una matriz simétrica que se define para la derivación. ${\displaystyle a_{ij}={\frac {\partial {\vec {r}}}{\partial q_{i}}}\cdot {\frac {\partial {\vec {r}}}{\partial q_{j}}}}$

Invariancia bajo transformaciones de coordenadas.

En cada instante de tiempo t , la energía es invariante bajo cambios de coordenadas espaciales de configuración q → Q , es decir (usando coordenadas naturales)

${\displaystyle E(\mathbf {q} ,{\dot {\mathbf {q} }},t)=E(\mathbf {Q} ,{\dot {\mathbf {Q} }},t).}$

Además de este resultado, la siguiente prueba muestra que, bajo tal cambio de coordenadas, las derivadas cambian como coeficientes de forma lineal. ${\displaystyle \partial L/\partial {\dot {q}}_{i}}$

Conservación

En la mecánica lagrangiana, el sistema es cerrado si y sólo si su lagrangiano no depende explícitamente del tiempo. La ley de conservación de la energía establece que la energía de un sistema cerrado es una integral del movimiento . ${\displaystyle L}$ ${\displaystyle E}$

Más precisamente, sea q = q ( t ) un extremo . (En otras palabras, q satisface las ecuaciones de Euler-Lagrange). Tomando la derivada temporal total de L a lo largo de este extremo y usando las ecuaciones EL se obtiene

${\displaystyle {\begin{aligned}{\frac {dL}{dt}}={\dot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {q} }}+{\ddot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {\dot {q}} }}+{\frac {\partial L}{\partial t}}\\-{\frac {\partial L}{\partial t}}={\frac {d}{dt}}\left({\frac {\partial L}{\partial \mathbf {\dot {q}} }}\right){\dot {\mathbf {q} }}+{\ddot {\mathbf {q} }}{\frac {\partial L}{\partial \mathbf {\dot {q}} }}-{\dot {L}}\\-{\frac {\partial L}{\partial t}}={\frac {d}{dt}}\left({\frac {\partial L}{\partial \mathbf {\dot {q}} }}\mathbf {\dot {q}} -L\right)={\frac {dH}{dt}}\end{aligned}}}$

Si el Lagrangiano L no depende explícitamente del tiempo, entonces ∂ L /∂ t = 0 , entonces H no varía con el tiempo la evolución de la partícula, de hecho, es una integral de movimiento, lo que significa que

${\displaystyle H(\mathbf {q} (t),{\dot {\mathbf {q} }}(t),t)={\text{constant of time}}.}$

Por tanto, si las coordenadas elegidas fueran coordenadas naturales, la energía se conserva.

Energías cinéticas y potenciales.

En todas estas circunstancias, ^[34] la constante

${\displaystyle E=T+V}$

es la energía total del sistema. Las energías cinética y potencial todavía cambian a medida que el sistema evoluciona, pero el movimiento del sistema será tal que su suma, la energía total, sea constante. Esta es una simplificación valiosa, ya que la energía E es una constante de integración que cuenta como una constante arbitraria para el problema, y ​​puede ser posible integrar las velocidades de esta relación de energía para resolver las coordenadas.

Similitud mecánica

Si la energía potencial es una función homogénea de las coordenadas e independiente del tiempo, ^[35] y todos los vectores de posición están escalados por la misma constante distinta de cero α , r _k ′ = α r _k , de modo que

${\displaystyle V(\alpha \mathbf {r} _{1},\alpha \mathbf {r} _{2},\ldots ,\alpha \mathbf {r} _{N})=\alpha ^{N}V(\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,\mathbf {r} _{N})}$

y el tiempo se escala por un factor β , t ′ = βt , entonces las velocidades v _k se escalan por un factor de α / β y la energía cinética T por ( α / β ) ² . Todo el lagrangiano ha sido escalado por el mismo factor si

${\displaystyle {\frac {\alpha ^{2}}{\beta ^{2}}}=\alpha ^{N}\quad \Rightarrow \quad \beta =\alpha ^{1-{\frac {N}{2}}}\,.}$

Dado que las longitudes y los tiempos han sido escalados, las trayectorias de las partículas en el sistema siguen trayectorias geométricamente similares que difieren en tamaño. La longitud l recorrida en el tiempo t en la trayectoria original corresponde a una nueva longitud l ′ recorrida en el tiempo t ′ en la nueva trayectoria, dada por las razones

${\displaystyle {\frac {t'}{t}}=\left({\frac {l'}{l}}\right)^{1-{\frac {N}{2}}}\,.}$

Partículas que interactúan

Para un sistema dado, si dos subsistemas _A y B no interactúan, el lagrangiano L del sistema general es la suma de los lagrangianos L _A y LB para los subsistemas: ^[30]

${\displaystyle L=L_{A}+L_{B}\,.}$

Si interactúan, esto no es posible. En algunas situaciones, puede ser posible separar el lagrangiano del sistema L en la suma de los lagrangianos que no interactúan, más otro lagrangiano L _AB que contenga información sobre la interacción,

${\displaystyle L=L_{A}+L_{B}+L_{AB}\,.}$

Esto puede estar motivado físicamente al tomar los lagrangianos que no interactúan como energías cinéticas únicamente, mientras que el lagrangiano de interacción es la energía potencial total del sistema. Además, en el caso límite de interacción insignificante, LA _AB tiende a cero reduciéndose al caso anterior de no interacción.

La extensión a más de dos subsistemas que no interactúan es sencilla: el lagrangiano general es la suma de los lagrangianos separados para cada subsistema. Si hay interacciones, entonces se pueden agregar interacciones lagrangianas.

Consecuencias de los lagrangianos singulares

De las ecuaciones de Euler-Lagrange se deduce que:

${\displaystyle {\begin{aligned}{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-{\frac {\partial L}{\partial q_{i}}}=0\\{\frac {\partial ^{2}L}{\partial q_{j}\partial {\dot {q}}_{i}}}{\frac {dq_{j}}{dt}}+{\frac {\partial ^{2}L}{\partial {\dot {q}}_{j}\partial {\dot {q}}_{i}}}{\frac {d{\dot {q}}_{j}}{dt}}+{\frac {\partial L}{\partial t}}-{\frac {\partial L}{\partial q_{i}}}=0\\\sum _{j}W_{ij}(q,{\dot {q}},t){\ddot {q}}_{j}={\frac {\partial L}{\partial q_{i}}}-{\frac {\partial L}{\partial t}}-\sum _{j}{\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial q_{j}}}{\dot {q}}_{j}\\\end{aligned}}}$

Donde la matriz se define como . Si la matriz no es singular, las ecuaciones anteriores se pueden resolver para representarlas en función de . Si la matriz no es invertible, no sería posible representar todos los s en función de pero, además, las ecuaciones de movimiento hamiltonianas no tomarán la forma estándar. ^[36] ${\displaystyle W_{ij}={\frac {\partial ^{2}L}{\partial {\dot {q}}_{i}\partial {\dot {q}}_{j}}}}$ ${\displaystyle W}$ ${\displaystyle {\ddot {q}}}$ ${\displaystyle ({\dot {q}},q,t)}$ ${\displaystyle {\ddot {q}}}$ ${\displaystyle ({\dot {q}},q,t)}$

Ejemplos

Los siguientes ejemplos aplican las ecuaciones de Lagrange del segundo tipo a problemas mecánicos.

Fuerza conservadora

Una partícula de masa m se mueve bajo la influencia de una fuerza conservativa derivada del gradiente ∇ de un potencial escalar ,

${\displaystyle \mathbf {F} =-{\boldsymbol {\nabla }}V(\mathbf {r} )\,.}$

Si hay más partículas, de acuerdo con los resultados anteriores, la energía cinética total es una suma de todas las energías cinéticas de las partículas y el potencial es función de todas las coordenadas.

Coordenadas cartesianas

El lagrangiano de la partícula se puede escribir

${\displaystyle L(x,y,z,{\dot {x}},{\dot {y}},{\dot {z}})={\frac {1}{2}}m({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2})-V(x,y,z)\,.}$

Las ecuaciones de movimiento de la partícula se encuentran aplicando la ecuación de Euler-Lagrange , para la coordenada x .

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {x}}}}\right)={\frac {\partial L}{\partial x}}\,,}$

con derivados

${\displaystyle {\frac {\partial L}{\partial x}}=-{\frac {\partial V}{\partial x}}\,,\quad {\frac {\partial L}{\partial {\dot {x}}}}=m{\dot {x}}\,,\quad {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {x}}}}\right)=m{\ddot {x}}\,,}$

por eso

${\displaystyle m{\ddot {x}}=-{\frac {\partial V}{\partial x}}\,,}$

y lo mismo para las coordenadas y y z . Recogiendo las ecuaciones en forma vectorial encontramos

${\displaystyle m{\ddot {\mathbf {r} }}=-{\boldsymbol {\nabla }}V}$

que es la segunda ley del movimiento de Newton para una partícula sujeta a una fuerza conservativa.

Coordenadas polares en 2D y 3D

Usando las coordenadas esféricas ( r , θ , φ ) como se usan comúnmente en física (convención ISO 80000-2:2019), donde r es la distancia radial al origen, θ es el ángulo polar (también conocido como colatitud, ángulo cenital, ángulo normal , o ángulo de inclinación), y φ es el ángulo azimutal, el lagrangiano para un potencial central es

${\displaystyle L={\frac {m}{2}}({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+r^{2}\sin ^{2}\theta \,{\dot {\varphi }}^{2})-V(r)\,.}$

Entonces, en coordenadas esféricas, las ecuaciones de Euler-Lagrange son

${\displaystyle m{\ddot {r}}-mr({\dot {\theta }}^{2}+\sin ^{2}\theta \,{\dot {\varphi }}^{2})+{\frac {\partial V}{\partial r}}=0\,,}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}(mr^{2}{\dot {\theta }})-mr^{2}\sin \theta \cos \theta \,{\dot {\varphi }}^{2}=0\,,}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}(mr^{2}\sin ^{2}\theta \,{\dot {\varphi }})=0\,.}$

La coordenada φ es cíclica ya que no aparece en el Lagrangiano, por lo que el momento conservado en el sistema es el momento angular.

${\displaystyle p_{\varphi }={\frac {\partial L}{\partial {\dot {\varphi }}}}=mr^{2}\sin ^{2}\theta {\dot {\varphi }}\,,}$

en el que r , θ y dφ / dt pueden variar con el tiempo, pero sólo de tal manera que p _φ sea constante.

El lagrangiano en coordenadas polares bidimensionales se recupera fijando θ al valor constante π /2.

Péndulo sobre soporte móvil

Croquis de la situación con definición de las coordenadas (click para ampliar)

Considere un péndulo de masa m y longitud ℓ , que está unido a un soporte con masa M , que puede moverse a lo largo de una línea en la dirección -. Sea la coordenada a lo largo de la línea del soporte y denotemos la posición del péndulo por el ángulo con la vertical. Las coordenadas y componentes de velocidad de la masa del péndulo son ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle \theta }$

${\displaystyle {\begin{array}{rll}&x_{\mathrm {pend} }=x+\ell \sin \theta &\quad \Rightarrow \quad {\dot {x}}_{\mathrm {pend} }={\dot {x}}+\ell {\dot {\theta }}\cos \theta \\&y_{\mathrm {pend} }=-\ell \cos \theta &\quad \Rightarrow \quad {\dot {y}}_{\mathrm {pend} }=\ell {\dot {\theta }}\sin \theta \,.\end{array}}}$

Las coordenadas generalizadas se pueden tomar como y . La energía cinética del sistema es entonces ${\displaystyle x}$ ${\displaystyle \theta }$

${\displaystyle T={\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left({\dot {x}}_{\mathrm {pend} }^{2}+{\dot {y}}_{\mathrm {pend} }^{2}\right)}$

y la energía potencial es

${\displaystyle V=mgy_{\mathrm {pend} }}$

dando el lagrangiano

${\displaystyle {\begin{array}{rcl}L&=&T-V\\&=&{\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left[\left({\dot {x}}+\ell {\dot {\theta }}\cos \theta \right)^{2}+\left(\ell {\dot {\theta }}\sin \theta \right)^{2}\right]+mg\ell \cos \theta \\&=&{\frac {1}{2}}\left(M+m\right){\dot {x}}^{2}+m{\dot {x}}\ell {\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^{2}{\dot {\theta }}^{2}+mg\ell \cos \theta \,.\end{array}}}$

Como x está ausente en el lagrangiano, es una coordenada cíclica. El impulso conservado es

${\displaystyle p_{x}={\frac {\partial L}{\partial {\dot {x}}}}=(M+m){\dot {x}}+m\ell {\dot {\theta }}\cos \theta \,}$

y la ecuación de Lagrange para la coordenada de apoyo es ${\displaystyle x}$

${\displaystyle (M+m){\ddot {x}}+m\ell {\ddot {\theta }}\cos \theta -m\ell {\dot {\theta }}^{2}\sin \theta =0\,.}$

La ecuación de Lagrange para el ángulo θ es

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left[m({\dot {x}}\ell \cos \theta +\ell ^{2}{\dot {\theta }})\right]+m\ell ({\dot {x}}{\dot {\theta }}+g)\sin \theta =0;}$

y simplificando

${\displaystyle {\ddot {\theta }}+{\frac {\ddot {x}}{\ell }}\cos \theta +{\frac {g}{\ell }}\sin \theta =0.}$

Estas ecuaciones pueden parecer bastante complicadas, pero encontrarlas con las leyes de Newton habría requerido identificar cuidadosamente todas las fuerzas, lo que habría sido mucho más laborioso y propenso a errores. Al considerar casos límite, se puede verificar la exactitud de este sistema: por ejemplo, se deben dar las ecuaciones de movimiento para un péndulo simple que está en reposo en algún sistema inercial , mientras que se deben dar las ecuaciones para un péndulo en un sistema en constante aceleración, etc. Además, es trivial obtener los resultados numéricamente, dadas las condiciones iniciales adecuadas y un paso de tiempo elegido, repasando los resultados de forma iterativa . ${\displaystyle {\ddot {x}}\to 0}$ ${\displaystyle {\ddot {\theta }}\to 0}$

Problema de fuerza central de dos cuerpos

Dos cuerpos de masas m ₁ y m ₂ con vectores de posición r ₁ y r ₂ están en órbita uno alrededor del otro debido a un potencial central atractivo V . Podemos escribir el lagrangiano en términos de las coordenadas de posición tal como están, pero es un procedimiento establecido convertir el problema de dos cuerpos en un problema de un cuerpo de la siguiente manera. Introduzca las coordenadas de Jacobi ; la separación de los cuerpos r = r ₂ − r ₁ y la ubicación del centro de masa R = ( m ₁ r ₁ + m ₂ r ₂ )/( m ₁ + m ₂ ) . El lagrangiano es entonces ^{[37] [38] [nb 4]}

${\displaystyle L=\underbrace {{\frac {1}{2}}M{\dot {\mathbf {R} }}^{2}} _{L_{\text{cm}}}+\underbrace {{\frac {1}{2}}\mu {\dot {\mathbf {r} }}^{2}-V(|\mathbf {r} |)} _{L_{\text{rel}}}}$

donde M = m ₁ + m ₂ es la masa total, μ = m ₁ m ₂ /( m ₁ + m ₂ ) es la masa reducida y V el potencial de la fuerza radial, que depende sólo de la magnitud de la separación. | r | = | r ₂ - r ₁ | . El lagrangiano se divide en un término de centro de masa L _cm y un término de movimiento relativo L _rel .

La ecuación de Euler-Lagrange para R es simplemente

${\displaystyle M{\ddot {\mathbf {R} }}=0\,,}$

que establece que el centro de masa se mueve en línea recta a velocidad constante.

Dado que el movimiento relativo sólo depende de la magnitud de la separación, lo ideal es utilizar coordenadas polares ( r , θ ) y tomar r = | r | ,

${\displaystyle L_{\text{rel}}={\frac {1}{2}}\mu ({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2})-V(r)\,,}$

entonces θ es una coordenada cíclica con el correspondiente momento (angular) conservado

${\displaystyle p_{\theta }={\frac {\partial L_{\text{rel}}}{\partial {\dot {\theta }}}}=\mu r^{2}{\dot {\theta }}=\ell \,.}$

La coordenada radial r y la velocidad angular d θ /d t pueden variar con el tiempo, pero solo de tal manera que ℓ sea constante. La ecuación de Lagrange para r es

${\displaystyle \mu r{\dot {\theta }}^{2}-{\frac {dV}{dr}}=\mu {\ddot {r}}\,.}$

Esta ecuación es idéntica a la ecuación radial obtenida usando las leyes de Newton en un sistema de referencia co-rotativo , es decir, un sistema que gira con la masa reducida de modo que parece estacionario. Eliminando la velocidad angular d θ /d t de esta ecuación radial, ^[39]

${\displaystyle \mu {\ddot {r}}=-{\frac {\mathrm {d} V}{\mathrm {d} r}}+{\frac {\ell ^{2}}{\mu r^{3}}}\,.}$

que es la ecuación de movimiento para un problema unidimensional en el que una partícula de masa μ está sometida a la fuerza central hacia adentro −d V /d r y una segunda fuerza hacia afuera, llamada en este contexto fuerza centrífuga (lagrangiana) (ver fuerza centrífuga#Otros usos del término ):

${\displaystyle F_{\mathrm {cf} }=\mu r{\dot {\theta }}^{2}={\frac {\ell ^{2}}{\mu r^{3}}}\,.}$

Por supuesto, si uno permanece completamente dentro de la formulación unidimensional, ℓ entra sólo como algún parámetro impuesto de la fuerza externa hacia afuera, y su interpretación como momento angular depende del problema bidimensional más general del cual se originó el problema unidimensional. .

Si se llega a esta ecuación utilizando la mecánica newtoniana en un marco co-rotativo, la interpretación es evidente como la fuerza centrífuga en ese marco debido a la rotación del propio marco. Si uno llega a esta ecuación directamente usando las coordenadas generalizadas ( r , θ ) y simplemente siguiendo la formulación lagrangiana sin pensar en marcos en absoluto, la interpretación es que la fuerza centrífuga es una consecuencia del uso de coordenadas polares . Como dice Hildebrand: ^[40]

"Dado que tales cantidades no son verdaderas fuerzas físicas, a menudo se las llama fuerzas de inercia . Su presencia o ausencia depende, no del problema particular en cuestión, sino del sistema de coordenadas elegido ". En particular, si se eligen coordenadas cartesianas, la fuerza centrífuga desaparece y la formulación involucra sólo la fuerza central misma, que proporciona la fuerza centrípeta para un movimiento curvo.

Este punto de vista, de que las fuerzas ficticias se originan en la elección de las coordenadas, a menudo lo expresan los usuarios del método lagrangiano. Esta visión surge naturalmente en el enfoque lagrangiano, porque el marco de referencia se selecciona (posiblemente inconscientemente) mediante la elección de coordenadas. Por ejemplo, ver ^[41] para una comparación de lagrangianos en un marco de referencia inercial y no inercial. Véase también la discusión sobre las formulaciones lagrangianas "totales" y "actualizadas" en ^[42] Desafortunadamente, este uso de "fuerza de inercia" entra en conflicto con la idea newtoniana de una fuerza de inercia. Desde el punto de vista newtoniano, una fuerza de inercia se origina en la aceleración del sistema de observación (el hecho de que no sea un sistema de referencia inercial ), no en la elección del sistema de coordenadas. Para dejar las cosas claras, es más seguro referirse a las fuerzas de inercia lagrangianas como fuerzas de inercia generalizadas , para distinguirlas de las fuerzas de inercia vectoriales newtonianas. Es decir, uno debería evitar seguir a Hildebrand cuando dice (p. 155) " siempre tratamos con fuerzas, velocidades, aceleraciones y momentos generalizados . Por brevedad, el adjetivo "generalizado" se omitirá con frecuencia".

Se sabe que el Lagrangiano de un sistema no es único. Dentro del formalismo lagrangiano, las fuerzas ficticias newtonianas pueden identificarse por la existencia de lagrangianos alternativos en los que las fuerzas ficticias desaparecen, a veces encontradas explotando la simetría del sistema. ^[43]

Extensiones para incluir fuerzas no conservadoras

Fuerzas disipativas

La disipación (es decir, los sistemas no conservadores) también se puede tratar con un lagrangiano eficaz formulado mediante una cierta duplicación de los grados de libertad. ^{[44] [45] [46] [47]}

En una formulación más general, las fuerzas podrían ser tanto conservadoras como viscosas . Si se puede encontrar una transformación apropiada a partir de F _i , Rayleigh sugiere usar una función de disipación , D , de la siguiente forma: ^[48]

${\displaystyle D={\frac {1}{2}}\sum _{j=1}^{m}\sum _{k=1}^{m}C_{jk}{\dot {q}}_{j}{\dot {q}}_{k}\,}$

donde C _jk son constantes relacionadas con los coeficientes de amortiguamiento del sistema físico, aunque no necesariamente iguales a ellos. Si D se define de esta manera, entonces ^[48]

${\displaystyle Q_{j}=-{\frac {\partial V}{\partial q_{j}}}-{\frac {\partial D}{\partial {\dot {q}}_{j}}}}$

y

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial L}{\partial q_{j}}}+{\frac {\partial D}{\partial {\dot {q}}_{j}}}=0\,.}$

Electromagnetismo

Una partícula de prueba es una partícula cuya masa y carga se supone que son tan pequeñas que su efecto sobre el sistema externo es insignificante. A menudo es una partícula puntual hipotética simplificada sin más propiedades que la masa y la carga. Las partículas reales como los electrones y los quarks up son más complejas y tienen términos adicionales en sus lagrangianos. Los campos no sólo pueden formar potenciales no conservativos, sino que estos potenciales también pueden depender de la velocidad.

El lagrangiano para una partícula cargada con carga eléctrica q , que interactúa con un campo electromagnético , es el ejemplo prototípico de un potencial dependiente de la velocidad. El potencial escalar eléctrico ϕ = ϕ ( r , t ) y el potencial vectorial magnético A = A ( r , t ) se definen a partir del campo eléctrico E = E ( r , t ) y el campo magnético B = B ( r , t ) como sigue:

${\displaystyle \mathbf {E} =-{\boldsymbol {\nabla }}\phi -{\frac {\partial \mathbf {A} }{\partial t}}\,,\quad \mathbf {B} ={\boldsymbol {\nabla }}\times \mathbf {A} \,.}$

El lagrangiano de una partícula de prueba masiva cargada en un campo electromagnético

${\displaystyle L={\tfrac {1}{2}}m{\dot {\mathbf {r} }}^{2}+q\,{\dot {\mathbf {r} }}\cdot \mathbf {A} -q\phi \,,}$

se llama acoplamiento mínimo . Este es un buen ejemplo de cuando la regla general común de que el lagrangiano es la energía cinética menos la energía potencial es incorrecta. Combinado con la ecuación de Euler-Lagrange , produce la ley de fuerza de Lorentz.

${\displaystyle m{\ddot {\mathbf {r} }}=q\mathbf {E} +q{\dot {\mathbf {r} }}\times \mathbf {B} }$

Transformación bajo calibre :

${\displaystyle \mathbf {A} \rightarrow \mathbf {A} +{\boldsymbol {\nabla }}f\,,\quad \phi \rightarrow \phi -{\dot {f}}\,,}$

donde f ( r ,t) es cualquier función escalar de espacio y tiempo, la transformada lagrangiana antes mencionada es como:

${\displaystyle L\rightarrow L+q\left({\dot {\mathbf {r} }}\cdot {\boldsymbol {\nabla }}+{\frac {\partial }{\partial t}}\right)f=L+q{\frac {df}{dt}}\,,}$

que todavía produce la misma ley de fuerza de Lorentz.

Tenga en cuenta que el momento canónico (conjugado con la posición r ) es el momento cinético más una contribución del campo A (conocido como momento potencial):

${\displaystyle \mathbf {p} ={\frac {\partial L}{\partial {\dot {\mathbf {r} }}}}=m{\dot {\mathbf {r} }}+q\mathbf {A} \,.}$

Esta relación también se utiliza en la prescripción de acoplamiento mínimo en mecánica cuántica y teoría cuántica de campos . A partir de esta expresión, podemos ver que el momento canónico p no es una invariante de calibre y, por lo tanto, no es una cantidad física mensurable; Sin embargo, si r es cíclico (es decir, lagrangiano es independiente de la posición r ), lo que sucede si los campos ϕ y A son uniformes, entonces este momento canónico p dado aquí es el momento conservado, mientras que el momento cinético físico medible m v no lo es.

Otros contextos y formulaciones

Las ideas de la mecánica lagrangiana tienen numerosas aplicaciones en otras áreas de la física y pueden adoptar resultados generalizados del cálculo de variaciones.

Formulaciones alternativas de la mecánica clásica.

Una formulación estrechamente relacionada de la mecánica clásica es la mecánica hamiltoniana . El hamiltoniano se define por

${\displaystyle H=\sum _{i=1}^{n}{\dot {q}}_{i}{\frac {\partial L}{\partial {\dot {q}}_{i}}}-L\,}$

y se puede obtener realizando una transformación de Legendre en el Lagrangiano, que introduce nuevas variables canónicamente conjugadas a las variables originales. Por ejemplo, dado un conjunto de coordenadas generalizadas, las variables canónicamente conjugadas son los momentos generalizados. Esto duplica el número de variables, pero hace que las ecuaciones diferenciales sean de primer orden. El hamiltoniano es una cantidad particularmente ubicua en la mecánica cuántica (ver Hamiltoniano (mecánica cuántica) ).

La mecánica de Routh es una formulación híbrida de la mecánica lagrangiana y hamiltoniana, que no se utiliza con frecuencia en la práctica, pero es una formulación eficiente para coordenadas cíclicas.

Formulación del espacio de momento.

Las ecuaciones de Euler-Lagrange también se pueden formular en términos de momentos generalizados en lugar de coordenadas generalizadas. Al realizar una transformación de Legendre en la coordenada generalizada Lagrangiana L ( q , d q /d t , t ) se obtienen los momentos generalizados Lagrangiano L ′( p , d p /d t , t ) en términos del Lagrangiano original, así como el EL ecuaciones en términos de momentos generalizados. Ambos lagrangianos contienen la misma información y cualquiera de ellos puede usarse para resolver el movimiento del sistema. En la práctica, las coordenadas generalizadas son más convenientes de usar e interpretar que los momentos generalizados.

Derivadas superiores de coordenadas generalizadas.

No existe ninguna razón matemática para restringir las derivadas de coordenadas generalizadas únicamente al primer orden. Es posible derivar ecuaciones EL modificadas para un lagrangiano que contenga derivadas de orden superior; consulte la ecuación de Euler-Lagrange para obtener más detalles. Sin embargo, desde el punto de vista físico existe un obstáculo para incluir derivadas temporales superiores al primer orden, lo que está implícito en la construcción de Ostrogradsky de un formalismo canónico para lagrangianos de derivadas superiores no degenerados, ver Inestabilidad de Ostrogradsky.

Óptica

La mecánica lagrangiana se puede aplicar a la óptica geométrica , aplicando principios variacionales a los rayos de luz en un medio, y resolviendo las ecuaciones EL se obtienen las ecuaciones de las trayectorias que siguen los rayos de luz.

Formulación relativista

La mecánica lagrangiana se puede formular en relatividad especial y relatividad general . Algunas características de la mecánica lagrangiana se conservan en las teorías relativistas, pero rápidamente aparecen dificultades en otros aspectos. En particular, las ecuaciones EL toman la misma forma y la conexión entre coordenadas cíclicas y momentos conservados todavía se aplica; sin embargo, el lagrangiano debe modificarse y no es simplemente la energía cinética menos la energía potencial de una partícula. Además, no es sencillo manejar sistemas multipartículas de forma manifiestamente covariante ; puede ser posible si se selecciona un marco de referencia particular.

Mecánica cuántica

En la mecánica cuántica , la acción y la fase mecánico-cuántica están relacionadas a través de la constante de Planck , y el principio de acción estacionaria puede entenderse en términos de interferencia constructiva de funciones de onda .

En 1948, Feynman descubrió la formulación de integral de trayectoria extendiendo el principio de mínima acción a la mecánica cuántica para electrones y fotones . En esta formulación, las partículas recorren todos los caminos posibles entre los estados inicial y final; la probabilidad de un estado final específico se obtiene sumando todas las trayectorias posibles que conducen a él. En el régimen clásico, la formulación integral de trayectoria reproduce claramente el principio de Hamilton y el principio de Fermat en óptica .

Teoría clásica de campos

En la mecánica lagrangiana, las coordenadas generalizadas forman un conjunto discreto de variables que definen la configuración de un sistema. En la teoría de campos clásica , el sistema físico no es un conjunto de partículas discretas, sino más bien un campo continuo ϕ ( r , t ) definido sobre una región del espacio 3D. Asociada con el campo hay una densidad lagrangiana.

${\displaystyle {\mathcal {L}}(\phi ,\nabla \phi ,\partial \phi /\partial t,\mathbf {r} ,t)}$

definido en términos del campo y sus derivadas de espacio y tiempo en una ubicación r y tiempo t . De manera análoga al caso de las partículas, para aplicaciones no relativistas, la densidad lagrangiana es también la densidad de energía cinética del campo, menos su densidad de energía potencial (esto no es cierto en general, y la densidad lagrangiana tiene que ser "ingeniería inversa"). El lagrangiano es entonces la integral de volumen de la densidad lagrangiana en el espacio 3D.

${\displaystyle L(t)=\int {\mathcal {L}}\,\mathrm {d} ^{3}\mathbf {r} }$

donde d ³ r es un elemento de volumen diferencial 3D . El lagrangiano es una función del tiempo ya que la densidad lagrangiana tiene una dependencia espacial implícita a través de los campos, y puede tener una dependencia espacial explícita, pero éstas se eliminan en la integral, dejando solo el tiempo como variable para el lagrangiano.

teorema de noether

El principio de acción y el formalismo lagrangiano están estrechamente vinculados al teorema de Noether , que conecta cantidades físicas conservadas con simetrías continuas de un sistema físico.

Si el lagrangiano es invariante bajo una simetría, entonces las ecuaciones de movimiento resultantes también son invariantes bajo esa simetría. Esta característica es muy útil para mostrar que las teorías son consistentes con la relatividad especial o la relatividad general .

Ver también

• Portal de astronomía

• Coordenadas canónicas
• Lema fundamental del cálculo de variaciones
• Derivado funcional
• Coordenadas generalizadas
• Mecánica hamiltoniana
• Óptica hamiltoniana
• Problema inverso de la mecánica lagrangiana , el tema general de encontrar un lagrangiano para un sistema dadas las ecuaciones de movimiento.
• Especificación lagrangiana y euleriana del campo de flujo.
• punto lagrangiano
• sistema lagrangiano
• Mecánica no autónoma
• El problema de la meseta
• Problema restringido de tres cuerpos

Notas a pie de página

1. A veces, en este contexto, la derivada variacional se denota y se define como
   $${\displaystyle {\frac {\delta }{\delta \mathbf {r} _{k}}}\equiv {\frac {\partial }{\partial \mathbf {r} _{k}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial }{\partial {\dot {\mathbf {r} }}_{k}}}}$$
   se utiliza. A lo largo de este artículo sólo se utilizan derivadas parciales y totales.
2. Aquí se supone que los desplazamientos virtuales son reversibles; es posible que algunos sistemas tengan desplazamientos virtuales no reversibles que violen este principio, consulte la ecuación de Udwadia-Kalaba .
3. En otras palabras
   $${\displaystyle \mathbf {C} _{k}\cdot \delta \mathbf {r} _{k}=0}$$
   para la partícula k sujeta a una fuerza de restricción, sin embargo
   $${\displaystyle C_{k\,x}\delta x_{k}\neq 0\,,\quad C_{k\,y}\delta y_{k}\neq 0\,,\quad C_{k\,z}\delta z_{k}\neq 0}$$
   debido a las ecuaciones de restricción en las _coordenadas rk .
4. El lagrangiano también se puede escribir explícitamente para un marco giratorio. Véase Padmanabhan, 2000.

Notas

1. Fraser, Craig. "Las primeras contribuciones de JL Lagrange a los principios y métodos de la mecánica". Archivo de Historia de las Ciencias Exactas, vol. 28, núm. 3, 1983, págs. 197–241. JSTOR, http://www.jstor.org/stable/41133689. Consultado el 3 de noviembre de 2023.
2. Mano y pinzón 1998, pag. 23
3. Hand & Finch 1998, págs. 18-20
4. Hand & Finch 1998, págs.46, 51
5. Torby 1984, pag. 270
6. Torby 1984, pag. 269
7. Mano y pinzón 1998, pag. 36–40
8. Mano y pinzón 1998, pag. 60–61
9. Mano y pinzón 1998, pag. 19
10. Penrose 2007
11. Kay 1988, pag. 156
12. Synge y Schild 1949, pág. 150-152
13. Foster y Nightingale 1995, pág. 89
14. Mano y pinzón 1998, pag. 4
15. Goldstein 1980, págs. 16-18
16. Mano y pinzón 1998, pag. 15
17. Mano y pinzón 1998, pag. 15
18. Fetter y Walecka 1980, pág. 53
19. Kibble y Berkshire 2004, pág. 234
20. Fetter y Walecka 1980, pág. 56
21. Mano y pinzón 1998, pag. 17
22. Mano y pinzón 1998, pag. 15-17
23. R. Penrose (2007). El camino a la realidad . Libros antiguos. pag. 474.ISBN _ 978-0-679-77631-4.
24. Goldstein 1980, pag. 23
25. Kibble y Berkshire 2004, pág. 234–235
26. Mano y pinzón 1998, pag. 51
27. Hand & Finch 1998, pág. 44–45
28. Goldstein 1980
29. Fetter y Walecka 1980, págs. 68–70
30. Landau y Lifshitz 1976, pág. 4
31. Goldstein, Poole y Safko 2002, pág. 21
32. Landau y Lifshitz 1976, pág. 4
33. Goldstein 1980, pag. 21
34. Landau y Lifshitz 1976, pág. 14
35. Landau y Lifshitz 1976, pág. 22
36. Rothe, Heinz J; Rothe, Klaus D (2010). Dinámica clásica y cuántica de sistemas hamiltonianos restringidos. Apuntes de conferencias científicas mundiales sobre física. vol. 81. CIENTÍFICO MUNDIAL. pag. 7. doi :10.1142/7689. ISBN 978-981-4299-64-0.
37. Taylor 2005, pag. 297
38. Padmanabhan 2000, pag. 48
39. Hand & Finch 1998, págs. 140-141
40. Hildebrand 1992, pag. 156
41. Zak, Zbilut y Meyers 1997, págs.202
42. Shabana 2008, págs. 118-119
43. Gannon 2006, pag. 267
44. Kosyakov 2007
45. Galera 2013
46. Birnholtz, Hadar y Kol 2014
47. Birnholtz, Hadar y Kol 2013
48. Torby 1984, pág. 271

Referencias

• Lagrange, JL (1811). Mécanique analytique. vol. 1.
• Lagrange, JL (1815). Mécanique analytique. vol. 2.
• Penrose, Roger (2007). El camino a la realidad . Libros antiguos. ISBN 978-0-679-77631-4.
• Landau, LD ; Lifshitz, EM (15 de enero de 1976). Mecánica (3ª ed.). Butterworth Heinemann. pag. 134.ISBN _ 9780750628969.
• Landau, Lev ; Lifshitz, Evgeny (1975). La teoría clásica de los campos . Elsevier Ltd. ISBN 978-0-7506-2768-9.
• Mano, LN; Pinzón, JD (1998). Mecánica analítica (2ª ed.). Prensa de la Universidad de Cambridge. ISBN 9780521575720.
• Saletán, EJ; José, JV (1998). Dinámica clásica: un enfoque contemporáneo. Prensa de la Universidad de Cambridge. ISBN 9780521636360.
• Croquetas, TWB; Berkshire, FH (2004). Mecánica clásica (5ª ed.). Prensa del Imperial College. pag. 236.ISBN _ 9781860944352.
• Goldstein, Herbert (1980). Mecánica clásica (2ª ed.). San Francisco, California: Addison Wesley. ISBN 0201029189.
• Goldstein, Herbert ; Poole, Charles P. Jr.; Safko, John L. (2002). Mecánica clásica (3ª ed.). San Francisco, California: Addison Wesley. ISBN 0-201-65702-3.
• Lanczos, Cornelio (1986). "II §5 Condiciones auxiliares: el método λ lagrangiano". Los principios variacionales de la mecánica (Reimpresión de la Universidad de Toronto 1970, 4ª ed.). Mensajero Dover. pag. 43.ISBN _ 0-486-65067-7.
• Grilletes, AL; Walecka, JD (1980). Mecánica Teórica de Partículas y Continua. Dover. págs. 53–57. ISBN 978-0-486-43261-8.
• El principio de mínima acción , R. Feynman
• Dvorak, R.; Freistetter, Florian (2005). "§ 3.2 Ecuaciones de Lagrange de primer tipo". Caos y estabilidad en los sistemas planetarios . Birkhäuser. pag. 24.ISBN _ 3-540-28208-4.
• Haken, H (2006). Información y autoorganización (3ª ed.). Saltador. pag. 61.ISBN _ 3-540-33021-6.
• Henry Zatzkis (1960). "§1.4 Ecuaciones de Lagrange de segundo tipo". En DH Menzel (ed.). Fórmulas fundamentales de la física . vol. 1 (2ª ed.). Mensajero Dover. pag. 160.ISBN _ 0-486-60595-7.
• Hildebrand, Francis Bégnaud (1992). Métodos de matemáticas aplicadas (Reimpresión de Prentice-Hall 1965, 2ª ed.). Mensajero Dover. pag. 156.ISBN _ 0-486-67002-3.
• Zak, Michael; Zbilut, José P.; Meyers, Ronald E. (1997). De la inestabilidad a la inteligencia. Saltador. pag. 202.ISBN _ 3-540-63055-4.
• Shabana, Ahmed A. (2008). Mecánica del continuo computacional. Prensa de la Universidad de Cambridge. págs. 118-119. ISBN 978-0-521-88569-0.
• Taylor, John Robert (2005). Mecanica clasica. Libros de ciencias universitarias. pag. 297.ISBN _ 1-891389-22-X.
• Padmanabhan, Thanu (2000). "§2.3.2 Movimiento en un marco giratorio". Astrofísica Teórica: Procesos astrofísicos (3ª ed.). Prensa de la Universidad de Cambridge. pag. 48.ISBN _ 0-521-56632-0.
• Doughty, Noel A. (1990). Interacción lagrangiana . Addison-Wesley Publishers Ltd. ISBN 0-201-41625-5.
• Kosyakov, BP (2007). Introducción a la teoría clásica de partículas y campos. Berlín, Alemania: Springer. doi :10.1007/978-3-540-40934-2. ISBN 978-3-540-40933-5.
• Galera, Chad R. (2013). "Mecánica clásica de sistemas no conservadores". Cartas de revisión física . 110 (17): 174301. arXiv : 1210.2745 . Código Bib : 2013PhRvL.110q4301G. doi : 10.1103/PhysRevLett.110.174301. PMID  23679733. S2CID  14591873.
• Birnholtz, Ofek; Hadar, Shahar; Kol, Barak (2014). "Reacción a la radiación a nivel de acción". Revista Internacional de Física Moderna A. 29 (24): 1450132–1450190. arXiv : 1402.2610 . Código Bib : 2014IJMPA..2950132B. doi :10.1142/S0217751X14501322. S2CID  118541484.
• Birnholtz, Ofek; Hadar, Shahar; Kol, Barak (2013). "Teoría de la radiación y reacción posnewtoniana". Revisión física D. 88 (10): 104037. arXiv : 1305.6930 . Código Bib : 2013PhRvD..88j4037B. doi : 10.1103/PhysRevD.88.104037. S2CID  119170985.
• Roger F Gans (2013). Dinámica de ingeniería: del lagrangiano a la simulación. Nueva York: Springer. ISBN 978-1-4614-3929-5.
• Gannon, Terry (2006). Luz de luna más allá del monstruo: el puente que conecta el álgebra, las formas modulares y la física. Prensa de la Universidad de Cambridge. pag. 267.ISBN _ 0-521-83531-3.
• Torby, Bruce (1984). "Métodos energéticos". Dinámica avanzada para ingenieros . Serie HRW en Ingeniería Mecánica. Estados Unidos de América: CBS College Publishing. ISBN 0-03-063366-4.
• fomentar, J; Ruiseñor, JD (1995). Un curso breve de relatividad general (2ª ed.). Saltador. ISBN 0-03-063366-4.
• el diputado Hobson; GP Efstathiou; AN Lasenby (2006). Relatividad general: una introducción para físicos. Prensa de la Universidad de Cambridge. págs. 79–80. ISBN 9780521829519.
• Synge, JL; Schild, A. (1949). Cálculo tensorial . Primera edición de 1978 de Dover Publications. ISBN 978-0-486-63612-2.
• Kay, David (abril de 1988). Esquema de Schaum del cálculo tensorial. Profesional de McGraw Hill. ISBN 978-0-07-033484-7.

Otras lecturas

• Gupta, Kiran Chandra, Mecánica clásica de partículas y cuerpos rígidos (Wiley, 1988).
• Cassel, Kevin (2013). Métodos variacionales con aplicaciones en ciencia e ingeniería . Cambridge: Prensa de la Universidad de Cambridge. ISBN 978-1-107-02258-4.
• Goldstein , Herbert y otros. Mecanica clasica . 3ª ed., Pearson, 2002.

enlaces externos

• David Tong. "Notas de conferencias de Cambridge sobre dinámica clásica". DAMTP . Consultado el 8 de junio de 2017 .
• Principio de mínima acción interactiva Excelente explicación/página web interactiva.
• Joseph Louis de Lagrange - Obras completas (Gallica-Math)
• Movimiento restringido y coordenadas generalizadas, página 4