Coordenadas generalizadas

Configuración del sistema respecto a otro.

En mecánica analítica , las coordenadas generalizadas son un conjunto de parámetros utilizados para representar el estado de un sistema en un espacio de configuración . Estos parámetros deben definir de forma única la configuración del sistema en relación con un estado de referencia. ^[1] Las velocidades generalizadas son las derivadas temporales de las coordenadas generalizadas del sistema. El adjetivo "generalizado" distingue estos parámetros del uso tradicional del término "coordenada" para referirse a las coordenadas cartesianas .

Un ejemplo de una coordenada generalizada sería describir la posición de un péndulo utilizando el ángulo del péndulo con respecto a la vertical, en lugar de mediante la posición xey del péndulo.

Aunque puede haber muchas opciones posibles para las coordenadas generalizadas de un sistema físico, generalmente se seleccionan para simplificar los cálculos, como la solución de las ecuaciones de movimiento del sistema. Si las coordenadas son independientes entre sí, el número de coordenadas generalizadas independientes está definido por el número de grados de libertad del sistema. ^{[2] [3]}

Las coordenadas generalizadas se combinan con momentos generalizados para proporcionar coordenadas canónicas en el espacio de fase .

Restricciones y grados de libertad.

Una coordenada generalizada (un grado de libertad) en caminos en 2D. Sólo se necesita una coordenada generalizada para especificar de forma única posiciones en la curva. En estos ejemplos, esa variable es la longitud del arco s o el ángulo θ . Tener ambas coordenadas cartesianas ( x , y ) es innecesario ya que x o y están relacionados entre sí mediante las ecuaciones de las curvas. También pueden parametrizarse por s o θ .

La longitud del arco s a lo largo de la curva es una coordenada generalizada legítima ya que la posición se determina de forma única, pero el ángulo θ no lo es ya que existen múltiples posiciones para un solo valor de θ .

Las coordenadas generalizadas generalmente se seleccionan para proporcionar el número mínimo de coordenadas independientes que definen la configuración de un sistema, lo que simplifica la formulación de las ecuaciones de movimiento de Lagrange . Sin embargo, también puede ocurrir que un conjunto útil de coordenadas generalizadas sea dependiente , lo que significa que están relacionadas por una o más ecuaciones de restricción .

Restricciones holonómicas

Dos coordenadas generalizadas, dos grados de libertad, en superficies curvas en 3D. Sólo se necesitan dos números ( u , v ) para especificar los puntos de la curva, se muestra una posibilidad para cada caso. Las tres coordenadas cartesianas completas ( x , y , z ) no son necesarias porque dos cualesquiera determinan la tercera según las ecuaciones de las curvas.

Para un sistema de N partículas en un espacio de coordenadas reales 3D , el vector de posición de cada partícula se puede escribir como una tupla triple en coordenadas cartesianas :

${\displaystyle {\begin{aligned}&\mathbf {r} _{1}=(x_{1},y_{1},z_{1}),\\&\mathbf {r} _{2}=(x_{2},y_{2},z_{2}),\\&\qquad \qquad \vdots \\&\mathbf {r} _{N}=(x_{N},y_{N},z_{N})\end{aligned}}}$

Cualquiera de los vectores de posición puede denotarse como r _k donde k = 1, 2,…, N etiqueta las partículas. Una restricción holonómica es una ecuación de restricción de la forma para la partícula k ^{[4] [a]}

${\displaystyle f(\mathbf {r} _{k},t)=0}$

que conecta las 3 coordenadas espaciales de esa partícula, por lo que no son independientes. La restricción puede cambiar con el tiempo, por lo que el tiempo t aparecerá explícitamente en las ecuaciones de restricción. En cualquier instante de tiempo, cualquier coordenada se determinará a partir de las otras coordenadas, por ejemplo, si se dan x _k y z _k , entonces también lo será y _k . Una ecuación de restricción cuenta como una restricción. Si hay restricciones C , cada una tiene una ecuación, por lo que habrá ecuaciones de restricciones C. No existe necesariamente una ecuación de restricción para cada partícula, y si no hay restricciones en el sistema, entonces no hay ecuaciones de restricción.

Hasta ahora, la configuración del sistema está definida por 3 N cantidades, pero se pueden eliminar las coordenadas C , una coordenada de cada ecuación de restricción. El número de coordenadas independientes es n = 3 N − C . (En dimensiones D , la configuración original necesitaría coordenadas ND , y la reducción por restricciones significa n = ND − C ). Es ideal utilizar la cantidad mínima de coordenadas necesarias para definir la configuración de todo el sistema, aprovechando al mismo tiempo las restricciones del sistema. Estas cantidades se conocen como coordenadas generalizadas en este contexto, denotadas q _j ( t ) . Es conveniente agruparlos en una n - tupla

${\displaystyle \mathbf {q} (t)=(q_{1}(t),\ q_{2}(t),\ \ldots ,\ q_{n}(t))}$

que es un punto en el espacio de configuración del sistema. Todos son independientes entre sí y cada uno es función del tiempo. Geométricamente pueden ser longitudes a lo largo de líneas rectas, o longitudes de arco a lo largo de curvas, o ángulos; no necesariamente coordenadas cartesianas u otras coordenadas ortogonales estándar . Hay una para cada grado de libertad , por lo que el número de coordenadas generalizadas es igual al número de grados de libertad, n . Un grado de libertad corresponde a una cantidad que cambia la configuración del sistema, por ejemplo el ángulo de un péndulo o la longitud del arco recorrido por una cuenta a lo largo de un alambre.

Si es posible encontrar a partir de las restricciones tantas variables independientes como grados de libertad, éstas pueden usarse como coordenadas generalizadas. ^[5] El vector de posición r _k de la partícula k es función de todas las n coordenadas generalizadas (y, a través de ellas, del tiempo), ^{[6] [7] [8] [5] [nb 1]}

${\displaystyle \mathbf {r} _{k}=\mathbf {r} _{k}(\mathbf {q} (t))\,,}$

y las coordenadas generalizadas pueden considerarse como parámetros asociados con la restricción.

Las correspondientes derivadas temporales de q son las velocidades generalizadas,

${\displaystyle {\dot {\mathbf {q} }}={\frac {d\mathbf {q} }{dt}}=({\dot {q}}_{1}(t),\ {\dot {q}}_{2}(t),\ \ldots ,\ {\dot {q}}_{n}(t))}$

(cada punto sobre una cantidad indica una derivada temporal ). El vector velocidad v _k es la derivada total de r _k con respecto al tiempo

${\displaystyle \mathbf {v} _{k}={\dot {\mathbf {r} }}_{k}={\frac {d\mathbf {r} _{k}}{dt}}=\sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}{\dot {q}}_{j}\,.}$

y por lo general depende de las velocidades y coordenadas generalizadas. Dado que somos libres de especificar los valores iniciales de las coordenadas generalizadas y las velocidades por separado, las coordenadas generalizadas q _j y las velocidades dq _j / dt pueden tratarse como variables independientes .

Restricciones no holonómicas

Un sistema mecánico puede implicar restricciones tanto en las coordenadas generalizadas como en sus derivadas. Las restricciones de este tipo se conocen como no holonómicas. Las restricciones no holonómicas de primer orden tienen la forma

${\displaystyle g(\mathbf {q} ,{\dot {\mathbf {q} }},t)=0\,,}$

Un ejemplo de tal restricción es una rueda rodante o el filo de una navaja que limita la dirección del vector velocidad. Las restricciones no holonómicas también pueden implicar derivadas de siguiente orden, como aceleraciones generalizadas.

Cantidades físicas en coordenadas generalizadas.

Energía cinética

La energía cinética total del sistema es la energía del movimiento del sistema, definida como ^[9]

${\displaystyle T={\frac {1}{2}}\sum _{k=1}^{N}m_{k}{\dot {\mathbf {r} }}_{k}\cdot {\dot {\mathbf {r} }}_{k}\,,}$

en el que · es el producto escalar . La energía cinética es función únicamente de las velocidades v _k , no de las coordenadas rk _mismas . Por el contrario, una observación importante es ^[10]

${\displaystyle {\dot {\mathbf {r} }}_{k}\cdot {\dot {\mathbf {r} }}_{k}=\sum _{i,j=1}^{n}\left({\frac {\partial \mathbf {r} _{k}}{\partial q_{i}}}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\right){\dot {q}}_{i}{\dot {q}}_{j},}$

lo que ilustra que la energía cinética es en general una función de las velocidades generalizadas, las coordenadas y el tiempo si las restricciones también varían con el tiempo, entonces T = T ( q , d q / dt , t ) .

En el caso de que las restricciones sobre las partículas sean independientes del tiempo, entonces todas las derivadas parciales con respecto al tiempo son cero y la energía cinética es una función homogénea de grado 2 en las velocidades generalizadas.

Aún para el caso independiente del tiempo, esta expresión equivale a tomar el elemento lineal al cuadrado de la trayectoria de la partícula k ,

${\displaystyle ds_{k}^{2}=d\mathbf {r} _{k}\cdot d\mathbf {r} _{k}=\sum _{i,j=1}^{n}\left({\frac {\partial \mathbf {r} _{k}}{\partial q_{i}}}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\right)dq_{i}dq_{j}\,,}$

y dividir por el diferencial cuadrado en el tiempo, dt ² , para obtener la velocidad al cuadrado de la partícula k . Por tanto, para restricciones independientes del tiempo es suficiente conocer el elemento lineal para obtener rápidamente la energía cinética de las partículas y, por tanto, la energía lagrangiana . ^[11]

Es instructivo ver los distintos casos de coordenadas polares en 2D y 3D, debido a su frecuente aparición. En coordenadas polares 2D ( r , θ ) ,

${\displaystyle \left({\frac {ds}{dt}}\right)^{2}={\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}\,,}$

en coordenadas cilíndricas 3D ( r , θ , z ) ,

${\displaystyle \left({\frac {ds}{dt}}\right)^{2}={\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+{\dot {z}}^{2}\,,}$

en coordenadas esféricas 3D ( r , θ , φ ) ,

${\displaystyle \left({\frac {ds}{dt}}\right)^{2}={\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+r^{2}\sin ^{2}\theta \,{\dot {\varphi }}^{2}\,.}$

Impulso generalizado

El momento generalizado " canónicamente conjugado con" la coordenada q _i se define por

${\displaystyle p_{i}={\frac {\partial L}{\partial {\dot {q}}_{i}}}.}$

Si la L lagrangiana no depende de alguna coordenada q _i , entonces de las ecuaciones de Euler-Lagrange se deduce que el momento generalizado correspondiente será una cantidad conservada , porque la derivada del tiempo es cero, lo que implica que el momento es una constante del movimiento;

${\displaystyle {\frac {\partial L}{\partial q_{i}}}={\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}={\dot {p}}_{i}=0\,.}$

Ejemplos

Cuenta en un alambre

Cuenta obligada a moverse sobre un alambre sin fricción. El alambre ejerce una fuerza de reacción C sobre la cuenta para mantenerla sobre el alambre. La fuerza no restrictiva N en este caso es la gravedad. Observe que la posición inicial del cable puede provocar diferentes movimientos.

Para una cuenta que se desliza sobre un alambre sin fricción sujeto solo a la gravedad en el espacio 2d, la restricción sobre la cuenta se puede expresar en la forma f ( r ) = 0 , donde la posición de la cuenta se puede escribir r = ( x ( s ) , y ( s )) , en el que s es un parámetro, la longitud del arco s a lo largo de la curva desde algún punto del cable. Ésta es una elección adecuada de coordenadas generalizadas para el sistema. Sólo se necesita una coordenada en lugar de dos, porque la posición de la cuenta se puede parametrizar mediante un número, s , y la ecuación de restricción conecta las dos coordenadas x e y ; cualquiera de los dos está determinado por el otro. La fuerza de restricción es la fuerza de reacción que el alambre ejerce sobre la cuenta para mantenerla sobre el alambre, y la fuerza aplicada sin restricción es la gravedad que actúa sobre la cuenta.

Supongamos que el alambre cambia de forma con el tiempo al flexionarse. Entonces la ecuación de restricción y la posición de la partícula son respectivamente

${\displaystyle f(\mathbf {r} ,t)=0\,,\quad \mathbf {r} =(x(s,t),y(s,t))}$

que ahora dependen del tiempo t debido al cambio de coordenadas a medida que el cable cambia de forma. Observe que el tiempo aparece implícitamente a través de las coordenadas y explícitamente en las ecuaciones de restricción.

Péndulo sencillo

Péndulo sencillo. Dado que la varilla es rígida, la posición de la masa está restringida según la ecuación f ( x , y ) = 0 , la fuerza de restricción C es la tensión en la varilla. Nuevamente, la fuerza no restrictiva N en este caso es la gravedad.

Modelo dinámico de un péndulo simple.

La relación entre el uso de coordenadas generalizadas y coordenadas cartesianas para caracterizar el movimiento de un sistema mecánico se puede ilustrar considerando la dinámica restringida de un péndulo simple. ^{[12] [13]}

Un péndulo simple consta de una masa M que cuelga de un punto de pivote de modo que se ve obligado a moverse en un círculo de radio L. La posición de la masa está definida por el vector de coordenadas r = ( x , y ) medido en el plano del círculo de modo que y esté en la dirección vertical. Las coordenadas x e y están relacionadas por la ecuación del círculo.

${\displaystyle f(x,y)=x^{2}+y^{2}-L^{2}=0,}$

que restringe el movimiento de M . Esta ecuación también proporciona una restricción sobre los componentes de la velocidad,

${\displaystyle {\dot {f}}(x,y)=2x{\dot {x}}+2y{\dot {y}}=0.}$

Ahora introduzca el parámetro θ , que define la posición angular de M desde la dirección vertical. Se puede utilizar para definir las coordenadas x e y , de modo que

${\displaystyle \mathbf {r} =(x,y)=(L\sin \theta ,-L\cos \theta ).}$

El uso de θ para definir la configuración de este sistema evita la restricción proporcionada por la ecuación del círculo.

Observe que la fuerza de gravedad que actúa sobre la masa m se formula en las coordenadas cartesianas habituales,

${\displaystyle \mathbf {F} =(0,-mg),}$

donde g es la aceleración debida a la gravedad .

El trabajo virtual de la gravedad sobre la masa m a medida que sigue la trayectoria r está dado por

${\displaystyle \delta W=\mathbf {F} \cdot \delta \mathbf {r} .}$

La variación δ r se puede calcular en términos de las coordenadas x e y , o en términos del parámetro θ ,

${\displaystyle \delta \mathbf {r} =(\delta x,\delta y)=(L\cos \theta ,L\sin \theta )\delta \theta .}$

Así, el trabajo virtual está dado por

${\displaystyle \delta W=-mg\delta y=-mgL\sin(\theta )\delta \theta .}$

Observe que el coeficiente de δ y es el componente y de la fuerza aplicada. De la misma manera, el coeficiente de δ θ se conoce como fuerza generalizada a lo largo de la coordenada generalizada θ , dada por

${\displaystyle F_{\theta }=-mgL\sin \theta .}$

Para completar el análisis considere la energía cinética T de la masa, usando la velocidad,

${\displaystyle \mathbf {v} =({\dot {x}},{\dot {y}})=(L\cos \theta ,L\sin \theta ){\dot {\theta }},}$

entonces,

${\displaystyle T={\frac {1}{2}}m\mathbf {v} \cdot \mathbf {v} ={\frac {1}{2}}m({\dot {x}}^{2}+{\dot {y}}^{2})={\frac {1}{2}}mL^{2}{\dot {\theta }}^{2}.}$

La forma de D'Alembert del principio de trabajo virtual para el péndulo en términos de las coordenadas xey están dadas por,

${\displaystyle {\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {x}}}}-{\frac {\partial T}{\partial x}}=F_{x}+\lambda {\frac {\partial f}{\partial x}},\quad {\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {y}}}}-{\frac {\partial T}{\partial y}}=F_{y}+\lambda {\frac {\partial f}{\partial y}}.}$

Esto produce las tres ecuaciones.

${\displaystyle m{\ddot {x}}=\lambda (2x),\quad m{\ddot {y}}=-mg+\lambda (2y),\quad x^{2}+y^{2}-L^{2}=0,}$

en las tres incógnitas, x , y y λ .

Usando el parámetro θ , esas ecuaciones toman la forma

${\displaystyle {\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {\theta }}}}-{\frac {\partial T}{\partial \theta }}=F_{\theta },}$

que se convierte,

${\displaystyle mL^{2}{\ddot {\theta }}=-mgL\sin \theta ,}$

o

${\displaystyle {\ddot {\theta }}+{\frac {g}{L}}\sin \theta =0.}$

Esta formulación produce una ecuación porque hay un solo parámetro y ninguna ecuación de restricción.

Esto muestra que el parámetro θ es una coordenada generalizada que se puede utilizar de la misma manera que las coordenadas cartesianas xey para analizar el péndulo.

Péndulo doble

Un doble péndulo

Los beneficios de las coordenadas generalizadas se hacen evidentes con el análisis de un péndulo doble . Para las dos masas m _i ( i = 1, 2) , sea r _i = ( x _i , y _i ), i = 1, 2 definir sus dos trayectorias. Estos vectores satisfacen las dos ecuaciones de restricción,

${\displaystyle f_{1}(x_{1},y_{1},x_{2},y_{2})=\mathbf {r} _{1}\cdot \mathbf {r} _{1}-L_{1}^{2}=0}$

y

${\displaystyle f_{2}(x_{1},y_{1},x_{2},y_{2})=(\mathbf {r} _{2}-\mathbf {r} _{1})\cdot (\mathbf {r} _{2}-\mathbf {r} _{1})-L_{2}^{2}=0.}$

La formulación de las ecuaciones de Lagrange para este sistema produce seis ecuaciones en las cuatro coordenadas cartesianas x _i , y _i ( i = 1, 2) y los dos multiplicadores de Lagrange λ _i ( i = 1, 2) que surgen de las dos ecuaciones de restricción.

Ahora introduzca las coordenadas generalizadas θ _i ( i = 1, 2) que definen la posición angular de cada masa del doble péndulo desde la dirección vertical. En este caso, tenemos

${\displaystyle \mathbf {r} _{1}=(L_{1}\sin \theta _{1},-L_{1}\cos \theta _{1}),\quad \mathbf {r} _{2}=(L_{1}\sin \theta _{1},-L_{1}\cos \theta _{1})+(L_{2}\sin \theta _{2},-L_{2}\cos \theta _{2}).}$

La fuerza de gravedad que actúa sobre las masas está dada por,

${\displaystyle \mathbf {F} _{1}=(0,-m_{1}g),\quad \mathbf {F} _{2}=(0,-m_{2}g)}$

donde g es la aceleración de la gravedad. Por lo tanto, el trabajo virtual de la gravedad sobre las dos masas a medida que siguen las trayectorias r _i ( i = 1, 2) viene dado por

${\displaystyle \delta W=\mathbf {F} _{1}\cdot \delta \mathbf {r} _{1}+\mathbf {F} _{2}\cdot \delta \mathbf {r} _{2}.}$

Las variaciones δ r _i ( i = 1, 2) se pueden calcular como

${\displaystyle \delta \mathbf {r} _{1}=(L_{1}\cos \theta _{1},L_{1}\sin \theta _{1})\delta \theta _{1},\quad \delta \mathbf {r} _{2}=(L_{1}\cos \theta _{1},L_{1}\sin \theta _{1})\delta \theta _{1}+(L_{2}\cos \theta _{2},L_{2}\sin \theta _{2})\delta \theta _{2}}$

Así, el trabajo virtual está dado por

${\displaystyle \delta W=-(m_{1}+m_{2})gL_{1}\sin \theta _{1}\delta \theta _{1}-m_{2}gL_{2}\sin \theta _{2}\delta \theta _{2},}$

y las fuerzas generalizadas son

${\displaystyle F_{\theta _{1}}=-(m_{1}+m_{2})gL_{1}\sin \theta _{1},\quad F_{\theta _{2}}=-m_{2}gL_{2}\sin \theta _{2}.}$

Calcule la energía cinética de este sistema como

${\displaystyle T={\frac {1}{2}}m_{1}\mathbf {v} _{1}\cdot \mathbf {v} _{1}+{\frac {1}{2}}m_{2}\mathbf {v} _{2}\cdot \mathbf {v} _{2}={\frac {1}{2}}(m_{1}+m_{2})L_{1}^{2}{\dot {\theta }}_{1}^{2}+{\frac {1}{2}}m_{2}L_{2}^{2}{\dot {\theta }}_{2}^{2}+m_{2}L_{1}L_{2}\cos(\theta _{2}-\theta _{1}){\dot {\theta }}_{1}{\dot {\theta }}_{2}.}$

La ecuación de Euler-Lagrange produce dos ecuaciones en las coordenadas generalizadas desconocidas θ _i ( i = 1, 2) dadas por ^[14]

${\displaystyle (m_{1}+m_{2})L_{1}^{2}{\ddot {\theta }}_{1}+m_{2}L_{1}L_{2}{\ddot {\theta }}_{2}\cos(\theta _{2}-\theta _{1})+m_{2}L_{1}L_{2}{\dot {\theta _{2}}}^{2}\sin(\theta _{1}-\theta _{2})=-(m_{1}+m_{2})gL_{1}\sin \theta _{1},}$

y

${\displaystyle m_{2}L_{2}^{2}{\ddot {\theta }}_{2}+m_{2}L_{1}L_{2}{\ddot {\theta }}_{1}\cos(\theta _{2}-\theta _{1})+m_{2}L_{1}L_{2}{\dot {\theta _{1}}}^{2}\sin(\theta _{2}-\theta _{1})=-m_{2}gL_{2}\sin \theta _{2}.}$

El uso de las coordenadas generalizadas θ _i ( i = 1, 2) proporciona una alternativa a la formulación cartesiana de la dinámica del doble péndulo.

Péndulo esférico

Péndulo esférico: ángulos y velocidades.

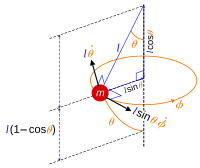
Para un ejemplo 3D, un péndulo esférico con longitud constante l libre de oscilar en cualquier dirección angular sujeto a la gravedad, la restricción sobre la masa del péndulo se puede expresar en la forma

${\displaystyle f(\mathbf {r} )=x^{2}+y^{2}+z^{2}-l^{2}=0\,,}$

donde se puede escribir la posición de la masa del péndulo

${\displaystyle \mathbf {r} =(x(\theta ,\phi ),y(\theta ,\phi ),z(\theta ,\phi ))\,,}$

en donde ( θ , φ ) son los ángulos polares esféricos debido a que la pesa se mueve en la superficie de una esfera. La posición r se mide a lo largo del punto de suspensión hasta la masa, tratada aquí como una partícula puntual . Una elección lógica de coordenadas generalizadas para describir el movimiento son los ángulos ( θ , φ ) . Solo se necesitan dos coordenadas en lugar de tres, porque la posición de la pesa se puede parametrizar mediante dos números y la ecuación de restricción conecta las tres coordenadas ( x , y , z ), de modo que cualquiera de ellas se determina a partir de las otras dos.

Coordenadas generalizadas y trabajo virtual.

El principio del trabajo virtual establece que si un sistema está en equilibrio estático, el trabajo virtual de las fuerzas aplicadas es cero para todos los movimientos virtuales del sistema desde este estado, es decir, δ W = 0 para cualquier variación δ r . ^[15] Cuando se formula en términos de coordenadas generalizadas, esto equivale al requisito de que las fuerzas generalizadas para cualquier desplazamiento virtual sean cero, es decir, F _i = 0 .

Sean las fuerzas sobre el sistema F _j ( j = 1, 2,…, m ) aplicadas a puntos con coordenadas cartesianas r _j ( j = 1, 2,…, m ) , entonces el trabajo virtual generado por un desplazamiento virtual desde la posición de equilibrio está dada por

${\displaystyle \delta W=\sum _{j=1}^{m}\mathbf {F} _{j}\cdot \delta \mathbf {r} _{j}.}$

donde δ r _j ( j = 1, 2,…, m ) denota los desplazamientos virtuales de cada punto del cuerpo.

Ahora supongamos que cada δ r _j depende de las coordenadas generalizadas q _i ( i = 1, 2,…, n ) entonces

${\displaystyle \delta \mathbf {r} _{j}={\frac {\partial \mathbf {r} _{j}}{\partial q_{1}}}\delta {q}_{1}+\ldots +{\frac {\partial \mathbf {r} _{j}}{\partial q_{n}}}\delta {q}_{n},}$

y

${\displaystyle \delta W=\left(\sum _{j=1}^{m}\mathbf {F} _{j}\cdot {\frac {\partial \mathbf {r} _{j}}{\partial q_{1}}}\right)\delta {q}_{1}+\ldots +\left(\sum _{j=1}^{m}\mathbf {F} _{j}\cdot {\frac {\partial \mathbf {r} _{j}}{\partial q_{n}}}\right)\delta {q}_{n}.}$

los n términos

${\displaystyle F_{i}=\sum _{j=1}^{m}\mathbf {F} _{j}\cdot {\frac {\partial \mathbf {r} _{j}}{\partial q_{i}}},\quad i=1,\ldots ,n,}$

son las fuerzas generalizadas que actúan sobre el sistema. Kane ^[16] muestra que estas fuerzas generalizadas también pueden formularse en términos de la relación de derivadas del tiempo,

${\displaystyle F_{i}=\sum _{j=1}^{m}\mathbf {F} _{j}\cdot {\frac {\partial \mathbf {v} _{j}}{\partial {\dot {q}}_{i}}},\quad i=1,\ldots ,n,}$

donde v _j es la velocidad del punto de aplicación de la fuerza F _j .

Para que el trabajo virtual sea cero para un desplazamiento virtual arbitrario, cada una de las fuerzas generalizadas debe ser cero, es decir

${\displaystyle \delta W=0\quad \Rightarrow \quad F_{i}=0,i=1,\ldots ,n.}$

Ver también

• Coordenadas canónicas
• Mecánica hamiltoniana
• Trabajo virtual
• Coordenadas ortogonales
• Coordenadas curvilíneas
• matriz de masa
• Matriz de rigidez
• Fuerzas generalizadas

Notas

1. Algunos autores, por ejemplo, Hand & Finch, toman la forma del vector de posición de la partícula k , como se muestra aquí, como condición para que la restricción de esa partícula sea holonómica.

1. Algunos autores establecen las ecuaciones de restricción en una constante por conveniencia con algunas ecuaciones de restricción (por ejemplo, péndulos), otros las establecen en cero. No hay diferencia porque la constante se puede restar para dar cero en un lado de la ecuación. Además, en las ecuaciones de Lagrange del primer tipo, sólo se necesitan las derivadas.

Referencias

1. Ginsberg 2008, pag. 397, §7.2.1 Selección de coordenadas generalizadas
2. Farid ML Amirouche (2006). "§2.4: Coordenadas generalizadas". Fundamentos de la dinámica multicuerpo: teoría y aplicaciones . Saltador. pag. 46.ISBN _ 0-8176-4236-6.
3. Florian Scheck (2010). "§5.1 Colectores de coordenadas generalizadas". Mecánica: de las leyes de Newton al caos determinista (5ª ed.). Saltador. pag. 286.ISBN _ 978-3-642-05369-6.
4. Goldstein, Poole y Safko 2002, pág. 12
5. Kibble y Berkshire 2004, pág. 232
6. Torby 1984, pag. 260
7. Goldstein, Poole y Safko 2002, pág. 13
8. Mano y pinzón 1998, pag. 15
9. Torby 1984, pag. 269
10. Goldstein, Poole y Safko 2002, pág. 25
11. Landau y Lifshitz 1976, pág. 8
12. Greenwood, Donald T. (1987). Principios de dinámica (2ª ed.). Prentice Hall. ISBN 0-13-709981-9.
13. Richard Fitzpatrick, Dinámica newtoniana.
14. Eric W. Weisstein, Péndulo doble, scienceworld.wolfram.com. 2007
15. Torby 1984
16. TR Kane y DA Levinson, Dinámica: teoría y aplicaciones, McGraw-Hill, Nueva York, 1985

Bibliografía de referencias citadas.

• Ginsberg, Jerry H. (2008). Dinámica de ingeniería (3ª ed.). Cambridge Reino Unido: Cambridge University Press . ISBN 978-0-521-88303-0.
• Goldstein, Herbert ; Poole, Carlos; Safko, Juan (2002). Mecánica clásica (3ª ed.). San Francisco, California: Addison Wesley. ISBN 0-201-65702-3.
• Mano, Luis N.; Pinzón, Janet D. (1998). Mecánica analítica . Cambridge: Prensa de la Universidad de Cambridge. ISBN 978-0521575720.
• Croquetas, TWB ; Berkshire, FH (2004). Mecánica clásica (5ª ed.). River Edge Nueva Jersey: Imperial College Press . ISBN 1860944248.
• Landau, LD; Lifshitz, EM (1976). Mecánica (Tercera ed.). Oxford. ISBN 978-0750628969.{{cite book}}: CS1 maint: location missing publisher (link)
• Torby, Bruce (1984). "Métodos energéticos". Dinámica avanzada para ingenieros . Serie HRW en Ingeniería Mecánica. Estados Unidos de América: CBS College Publishing. ISBN 0-03-063366-4.