Simetría (geometría)

Desde el punto de vista geométrico, un objeto posee simetría si existe una "operación" o "transformación" (como una isometría o una transformación afín) capaz de aplicar su figura sobre sí misma.

De forma análoga, se dice que el objeto es simétrico porque posee una invarianza con respecto a la transformación.

[1]​ Por ejemplo, un círculo girado alrededor de su centro tendrá la misma forma y tamaño que el círculo original: todos los puntos antes y después de la transformación serían indistinguibles.

[3]​ El grupo más común de transformaciones aplicadas a los objetos se denomina grupo euclídeo de "isometrías", que son transformaciones que conservan la distancia relativa entre sus puntos, comúnmente consideradas en el espacio bidimensional o tridimensional (es decir, en la geometría del plano o en la geometría del espacio).

Por ejemplo, en el caso de las reflexiones, una reflexión respecto a un punto (que produce una simetría como la de la letra "S"), es distinta a una simetría por afinidad (que produce una simetría bilateral respecto a un eje, como la que posee la letra "T").

Las "rotaciones" siempre se consideran respecto a un punto (el punto de giro), y las "traslaciones" son siempre transformaciones afines, puesto que implican desplazar formas paralelamente a sí mismas (por ejemplo, una cadena ilimitada de la misma letra repetida, poseería este tipo de simetría, denominada traslacional).

Otra forma de pensarlo es que si la forma se doblara por la mitad sobre el eje, las dos mitades serían idénticas: cada mitad es la imagen reflejada de la otra.

Por el mismo motivo, una circunferencia tiene infinitos ejes de simetría que pasan por su centro.

[7]​ Si la letra "T" se refleja respecto a un eje vertical, conserva exactamente la misma forma.

Se puede utilizar una formalización más precisa, como por ejemplo afirmando que "T tiene un eje de simetría vertical" o que "T tiene simetría de izquierda a derecha".

[10]​ Si k = m, dicha transformación se conoce como simetría central, o una inversión a través de un punto.

[12]​ Esto implica que para m = 3 (así como para otros m impares) un punto de reflexión cambia la orientación del espacio, como lo hace una simetría especular.

Las leyes de la física son invariantes con respecto a SO(3) si no se distinguen las diferentes direcciones del espacio.

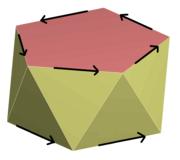
La simetría traslacional deja un objeto invariante en un grupo discreto o continuo de traslaciones

Si la línea de triángulos se extendiera hasta el infinito en ambas direcciones, se tendría una simetría traslacional discreta; cualquier traslación que asigne un triángulo a otro dejaría la línea entera sin cambios.

En 2D, una simetría de reflexión deslizada (en 3D se llama simetría respecto a un plano de deslizamiento, o en general, una transflexión) significa que una reflexión respecto a una línea o plano combinada con una traslación paralela a la línea o plano de simetría, da como resultado el mismo objeto.

El grupo de simetría que comprende reflexiones de deslizamiento y traslaciones asociadas es el friso p11g, y es isomorfo con el grupo cíclico infinito Z. En 3D, una reflexión giratoria, rotorreflexión o rotación impropia, consiste en una rotación sobre un eje combinada con la reflexión en un plano perpendicular a ese eje.

[26]​ Es similar al eje helicoidal en 3D, compuesto por una rotación y una traslación ortogonal.

Debido a que los fractales pueden generar la apariencia de patrones en la naturaleza, tienen una belleza y una familiaridad que no se ven normalmente en las funciones generadas matemáticamente.

Los fractales también han encontrado un lugar en la generación de efectos visuales digitales, donde su capacidad para crear curvas complejas con simetrías fractales da como resultado un mundo virtual más realista.

Por ejemplo, las longitudes, los ángulos y las áreas se conservan con respecto al grupo euclídeo de las simetrías, mientras que solo la estructura incidente y la razón anarmónica se conservan bajo las transformaciones proyectivas con carácter general.