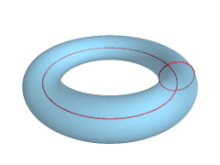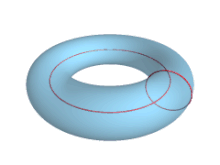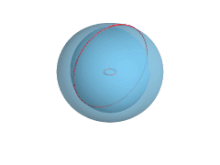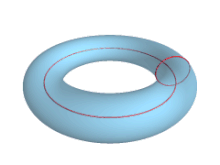
Toro (geometría)
La palabra «toro» proviene del latín torus, que significa «protuberancia», «elevación curva» (relacionado con latín sterno y griego στορέννυμι, romanizado storénnymi) y que ya en latín adquiere sentidos técnicos para designar objetos con esta forma geométrica específica, por ejemplo en arquitectura (Vitr.3.3.8), donde designa el «bocel» o «murecillo», que es una moldura redondeada de la base, con forma de hogaza de pan.
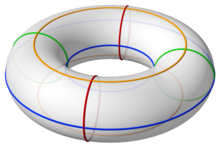
Puede demostrarse mediante el uso de cartas que el toro es una superficie regular.
Es por tanto importante notar que, salvo homeomorfismo, existen varias formas distintas y equivalentes de definir el toro.
El toro puede también describirse como un cociente del plano euclídeo bajo la identificación
con vértices (0,0), (1,0), (1,1) y (0,1)) generado mediante una identificación específica de los bordes opuestos.
El grupo fundamental del toro es, por las propiedades del grupo fundamental, precisamente el producto directo del grupo fundamental de la circunferencia por sí misma, es decir, se tiene: Intuitivamente, el que este grupo sea abeliano significa que un lazo que rodea primero el «agujero» y luego el «cuerpo» del toro (ambos de circunferencia con latitud concreta), se puede transformar en un camino que recorra primero el «cuerpo» y luego el «agujero».
En 3 dimensiones, se puede doblar una hoja plana de papel hasta formar un cilindro sin estirar el papel, pero este cilindro no se puede doblar hasta formar un toro sin estirar el papel (a menos que se abandonen algunas condiciones de regularidad y diferenciabilidad, véase más abajo).
No se puede incrustar analíticamente (mediante una función suave de clase Ck, 2 ≤ k ≤ ∞) en el espacio tridimensional euclidiano.
Por ejemplo, en la siguiente aplicación: Si R y P en la parametrización del toro plano anterior forman un vector unitario (R, P)= (cos(η), sin(η)), entonces u, v y 0 < η < π/2 parametrizan la 3-esfera unidad como un sistema de coordenadas de Hopf.
, o en otras palabras, Q es miembro del grupo de Lie SO(4).
Se sabe que no existe ninguna incrustación C2 (dos veces diferenciable continuamente) de un toro plano en el 3-espacio (la idea de la demostración es tomar una esfera grande que contenga un toro plano en su interior y reducir el radio de la esfera hasta que toque el toro por primera vez).
Pero eso implicaría que parte del toro, dado que tiene curvatura cero en todas partes, debe quedar estrictamente fuera de la esfera, lo cual es una contradicción.
Esto es únicamente una prueba de existencia y no proporciona ecuaciones explícitas para dicha incorporación.
Tiene una estructura similar a un fractal, ya que se construye corrugando repetidamente un toro común.
Al igual que los fractales, no tiene una curvatura gaussiana definida.
[7] Estas corrugaciones infinitamente recursivas se utilizan solo para incrustaciones en tres dimensiones, y no son una característica intrínseca del toro plano.
En el estudio de superficies de Riemann, se dice que dos superficies geométricas compactas y lisas son "conformemente equivalentes" cuando existe un homeomorfismo suave entre ellas que preserva el ángulo y la orientación.
M puede convertirse en un espacio compacto M* añadiendo un punto adicional que represente el caso límite cuando un toro rectangular se aproxima a una relación de aspecto de 0 en el límite.
Este punto adicional tendrá un ángulo cero a su alrededor.
Como resultado, el área de cada triángulo se puede calcular como π - (π/2 + π/3 + 0) = π/6, por lo que se deduce que el espacio de módulos compactados M* tiene un área igual a π/3.
Se puede generalizar fácilmente el toro a cualquier dimensión o potencia.
, se define como el producto de n circunferencias: El n-toro es
Equivalentemente, el n-toro se obtiene a partir del n-cubo pegando las caras opuestas.
cuyos generadores son los números duales enteros de los ciclos fundamentales a la potencia n. Si se toma idealmente una superficie rectangular flexible y extensible y se unen su lado superior con su lado inferior, y luego se unen los lados horizontales, resulta esta figura.
Uno debe respetar en el pegado la orientación de los bordes como el indicado en la figura.
En la figura anterior se observa que son necesarios siete colores.
En magnetismo, se enrolla una bobina con cierta cantidad de vueltas sobre el toro con un entrehierro (corte paralelo al eje que pasa por el centro del toro) para generar un campo magnético dentro del mismo.
En el mundo de los videojuegos de estrategia es fácil observar cómo los personajes que intervienen, cuando viajan hacia el norte reaparecen en el sur, como si le hubiesen dado la vuelta al mundo.
Asimismo, cuando llevan una trayectoria hacia el fondo en el oriente, reaparecen en el occidente y viceversa.
El sitio virtual donde este efecto acaece lleva el nombre de mundo toroide por las características matemáticas anteriormente descritas.