Cristalografía de rayos X
Von Laue, William Henry Bragg y William Lawrence Bragg desarrollaron inicialmente la teoría de difracción de cristales, tarea a la que pronto se sumaron otros científicos.
[1] En 1913, Paul Ewald demostró que las dos interpretaciones de los resultados publicadas independientemente por von Laue y Bragg eran equivalentes.
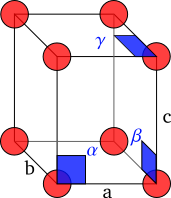
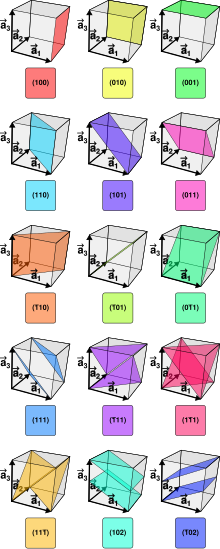
[10][11] El paralelepípedo definido por las líneas entre distintos nodos de la red se conoce como la celda unidad; aunque para una red dada sea posible designar múltiples celdas unidad que cumplan esta definición, por convención se escoge habitualmente la de menor volumen que refleje la simetría del cristal.
[16][17] Los rayos X se describen matemáticamente como una onda sinusoidal propagándose a través del espacio.
En un cristal, la diferencia en el camino óptico entre átomos situados en posiciones equivalentes en distintas celdas unidad es
La esfera de Ewald ilustra todas las posibles direcciones en que los rayos X pueden ser reflejados por el cristal.
en el sistema definido por la celda unidad y la suma se realiza para todos los átomos contenidos en ella.
se caracteriza por ser siempre positiva y alcanzar valores máximos alrededor de los átomos.
Los compuestos de mercurio, platino, uranio, y oro son los más utilizados, entre muchos otros.[43][n.
, si se repite el proceso con al menos una segunda estructura derivada diferente, es posible determinar las fases para la estructura nativa, por el método conocido como reemplazamiento isomorfo múltiple o sus siglas en inglés MIR (Multiple Isomorphous Replacement)[n. 13][44] Las principal limitación de este método estriba en la dificultad de encontrar compuestos que reaccionen con la molécula a estudiar sin destruir al mismo tiempo el cristal o modificar sensiblemente su simetría o las dimensiones de la celda unidad.
La ventaja de los métodos basados en la dispersión anómala es que, al precisar en principio solo un cristal para determinar las fases, no están limitados por un isomorfismo imperfecto.
Se usan dos técnicas matemáticas para ajustar los parámetros del modelo durante el refinamiento: los mínimos cuadrados y la máxima verosimilitud.
Aunque a veces es posible utilizar cristales de metales o minerales inorgánicos formados por medios naturales, a menudo es necesario prepararlos mediante recristalización o precipitación del material en una solución líquida sobresaturada en condiciones controladas de concentración y temperatura.
Posteriormente se introduce otra solución de un segundo reactante en la capa superior del gel, desde donde se difunde al resto de la matriz y reacciona con la primera sustancia para dar lugar a cristales.
[63] En los años 2000 se empezaron a utilizar fotodiodos alineados formando una placa, denominados PAD (Pixel Array Detectors).
Estos detectores se caracterizan por un gran margen dinámico y un tiempo muerto entre imágenes muy bajo, del orden de milisegundos.
Una nueva técnica, la cristalografía en serie, se ha desarrollado en las primeras décadas del siglo XXI.
En método de reflexión, el detector se encuentra entre la fuente y el cristal, para detectar los haces difractados hacia atrás.
En ambos métodos se usa una pantalla para medir solo una sección bidimensional de la red recíproca en cada imagen.
Los avances en computación de los años 90 posibilitaron un diseño más simple, en el que el detector se mantiene estacionario detrás del cristal, usándose programas para hallar automáticamente la orientación y los parámetros cristalinos consistentes con el patrón de difracción observado.
Este método se usa mayoritariamente cuando no es necesario determinar la estructura; por ejemplo, en el análisis de minerales presentes en una muestra.
[78][79][80] Asimismo, las diferencias en el patrón de difracción de diversos materiales,[81][82] hielo,[83] sean minerales, drogas, pigmentos, adsorbentes,[84] catalizadores,[85][86][87] etc., con aspectos y composiciones químicas similares son de mucha utilidad en la industria y campos sin relación directa con la investigación científica básica o el desarrollo tecnológico, como la ciencia forense o la historia del arte.
Asimismo, la técnica se ha usado para determinar la estructura de los fulerenos, materiales con interesantes propiedades físicas y químicas.
Cada sustancia mineral forma cristales con una celda unidad y simetría determinada, que resulta en un patrón de difracción característico.
En 1968, David DeRosier y Aaron Klug publicaron un método para reconstruir mapas de densidad electrónica tridimensionales basados en este principio.
[98] Hasta la segunda década del siglo XXI, la mejor resolución espacial de estos mapas —alrededor de 0,4 nm— era baja comparada con los valores alcanzables con rayos X o neutrones, aunque la criomicroscopía electrónica era útil en casos donde no era posible cristalizar la molécula a estudiar o la estructura no podía determinarse por otros métodos, principalmente en el ámbito de la biología macromolecular.
Aunque las técnicas cristalográficas pueden utilizarse también para determinar la estructura de otros materiales con periodicidad espacial, como fibras helicoidales —ADN, algunos tipos de virus, etc.— y cuasicristales, resulta imposible estudiar gases, líquidos y sólidos desordenados por este método.
[103] Otro límite de la técnica está relacionado con el tipo de información que proporciona sobre la estructura: Los modelos obtenidos por difracción representan una media de las posiciones atómicas para todas las moléculas del cristal; cuando la molécula cuenta con átomos que oscilan entre diferentes conformaciones, la densidad electrónica media se extiende sobre la totalidad del espacio que pueden ocupar estos átomos y las partes desordenadas de la molécula resultan invisibles.
Cuando esto ocurre, el modelo obtenido no refleja la verdadera estructura molecular y puede dar lugar a interpretaciones erróneas sobre sus propiedades.
Los experimentos con moléculas biológicas se suelen realizar a temperaturas de 100 K o menores; esto frena la difusión de los radicales libres, aunque no soluciona enteramente el problema, pues los fotoelectrones excitados por los rayos X permanecen móviles hasta el cero absoluto.