Transformada de Fourier

Mathematical transform that expresses a function of time as a function of frequency

Un ejemplo de aplicación de la transformada de Fourier es la determinación de los tonos constituyentes en una forma de onda musical . Esta imagen es el resultado de aplicar una transformada de Q constante (una transformada relacionada con Fourier ) a la forma de onda de un acorde de piano en do mayor . Los primeros tres picos de la izquierda corresponden a las frecuencias de la frecuencia fundamental del acorde (do, mi, sol). Los picos más pequeños restantes son armónicos de frecuencia más alta de los tonos fundamentales. Un algoritmo de detección de tonos podría utilizar la intensidad relativa de estos picos para inferir qué notas presionó el pianista.

En física , ingeniería y matemáticas , la transformada de Fourier ( FT ) es una transformada integral que toma una función como entrada y genera otra función que describe el grado en el que varias frecuencias están presentes en la función original. La salida de la transformada es una función de frecuencia de valor complejo . El término transformada de Fourier se refiere tanto a esta función de valor complejo como a la operación matemática . Cuando es necesario hacer una distinción, la salida de la operación a veces se denomina representación del dominio de frecuencia de la función original. La transformada de Fourier es análoga a descomponer el sonido de un acorde musical en las intensidades de sus tonos constituyentes .

La transformada de Fourier relaciona el dominio del tiempo, en rojo, con una función en el dominio de la frecuencia, en azul. Las frecuencias componentes, extendidas a todo el espectro de frecuencias, se muestran como picos en el dominio de la frecuencia.

La sinusoide roja se puede describir por la amplitud de pico (1), la relación pico a pico (2), el valor eficaz (3) y la longitud de onda (4). Las sinusoides roja y azul tienen una diferencia de fase de θ .

Las funciones que se localizan en el dominio del tiempo tienen transformadas de Fourier que se extienden a lo largo del dominio de la frecuencia y viceversa, un fenómeno conocido como el principio de incertidumbre. El caso crítico de este principio es la función gaussiana , de importancia sustancial en la teoría de la probabilidad y la estadística , así como en el estudio de los fenómenos físicos que exhiben una distribución normal (por ejemplo, la difusión ). La transformada de Fourier de una función gaussiana es otra función gaussiana. Joseph Fourier introdujo las transformadas de seno y coseno (que corresponden a los componentes imaginarios y reales de la transformada de Fourier moderna) en su estudio de la transferencia de calor , donde las funciones gaussianas aparecen como soluciones de la ecuación del calor .

La transformada de Fourier se puede definir formalmente como una integral de Riemann impropia , lo que la convierte en una transformada integral, aunque esta definición no es adecuada para muchas aplicaciones que requieren una teoría de integración más sofisticada. ^{[nota 1]} Por ejemplo, muchas aplicaciones relativamente simples utilizan la función delta de Dirac , que se puede tratar formalmente como si fuera una función, pero la justificación requiere un punto de vista matemáticamente más sofisticado. ^{[nota 2]}

La transformada de Fourier también se puede generalizar a funciones de varias variables en el espacio euclidiano , enviando una función del 'espacio de posición' tridimensional a una función del momento tridimensional (o una función del espacio y el tiempo a una función del momento cuatridimensional ). Esta idea hace que la transformada de Fourier espacial sea muy natural en el estudio de las ondas, así como en la mecánica cuántica , donde es importante poder representar soluciones de ondas como funciones de la posición o del momento y, a veces, de ambos. En general, las funciones a las que se aplican los métodos de Fourier son de valor complejo y, posiblemente, de valor vectorial . ^{[nota 3]} Es posible una generalización aún mayor a funciones sobre grupos , que, además de la transformada de Fourier original sobre R o R ⁿ , incluye notablemente la transformada de Fourier de tiempo discreto (DTFT, grupo = Z ), la transformada de Fourier discreta (DFT, grupo = Z mod N ) y la serie de Fourier o transformada de Fourier circular (grupo = S 1 , el círculo unitario ≈ intervalo finito cerrado con puntos finales identificados). Este último se emplea rutinariamente para manejar funciones periódicas . La transformada rápida de Fourier (FFT) es un algoritmo para calcular la DFT.

Definición

La transformada de Fourier es un proceso de análisis que descompone una función de valor complejo en sus frecuencias constituyentes y sus amplitudes. El proceso inverso es la síntesis , que recrea a partir de su transformada. ${\displaystyle \textstyle f(x)}$ ${\displaystyle \textstyle f(x)}$

Podemos empezar con una analogía, la serie de Fourier , que analiza en un intervalo acotado para algún número real positivo Las frecuencias constituyentes son un conjunto discreto de armónicos en frecuencias cuya amplitud y fase están dadas por la fórmula de análisis: La serie de Fourier real es la fórmula de síntesis: En un intervalo ilimitado, las frecuencias constituyentes son un continuo : ^{[1] [2] [3]} y se reemplaza por una función : ^[4] ${\displaystyle \textstyle f(x)}$ ${\displaystyle \textstyle x\in [-P/2,P/2],}$ ${\displaystyle P.}$ ${\displaystyle {\tfrac {n}{P}},n\in \mathbb {Z} ,}$ $${\displaystyle c_{n}={\frac {1}{P}}\int _{-P/2}^{P/2}f(x)\,e^{-i2\pi {\frac {n}{P}}x}\,dx.}$$ $${\displaystyle f(x)=\sum _{n=-\infty }^{\infty }c_{n}\,e^{i2\pi {\tfrac {n}{P}}x},\quad \textstyle x\in [-P/2,P/2].}$$ ${\displaystyle P\to \infty ,}$ ${\displaystyle {\tfrac {n}{P}}\to \xi \in \mathbb {R} ,}$ ${\displaystyle c_{n}}$

Transformada de Fourier

Evaluando la ecuación 1 para todos los valores de se obtiene la función en el dominio de la frecuencia . La integral puede divergir en algunas frecuencias. (ver § Transformada de Fourier para funciones periódicas) Pero converge para todas las frecuencias cuando decae con todas las derivadas como : . (Ver función de Schwartz ). Por el lema de Riemann-Lebesgue , la función transformada también decae con todas las derivadas. ${\displaystyle \xi }$ ${\displaystyle f(x)}$ ${\displaystyle x\to \pm \infty }$ ${\displaystyle \lim _{x\to \infty }f^{(n)}(x)=0,n=0,1,2,\dots }$ ${\displaystyle {\widehat {f}}}$

El número complejo , en coordenadas polares, transmite tanto la amplitud como la fase de la frecuencia. La interpretación intuitiva de la ecuación 1 es que el efecto de multiplicar por es restar de cada componente de frecuencia de la función ^{[nota 4].} Solo el componente que estaba en frecuencia puede producir un valor distinto de cero de la integral infinita, porque (al menos formalmente) todos los demás componentes desplazados son oscilatorios y se integran a cero. (ver § Ejemplo) ${\displaystyle {\widehat {f}}(\xi )}$ ${\displaystyle \xi .}$ ${\displaystyle f(x)}$ ${\displaystyle e^{-i2\pi \xi x}}$ ${\displaystyle \xi }$ ${\displaystyle f(x).}$ ${\displaystyle \xi }$

La fórmula de síntesis correspondiente es:

Transformada inversa

La ecuación 2 es una representación de una suma ponderada de funciones exponenciales complejas. ${\displaystyle f(x)}$

Esto también se conoce como el teorema de inversión de Fourier y se introdujo por primera vez en la teoría analítica del calor de Fourier . ^{[5] [6] [7] [8]}

Las funciones y se denominan pares de transformadas de Fourier . ^[9]   Una notación común para designar pares de transformadas es : ^[10]   por ejemplo   ${\displaystyle f}$ ${\displaystyle {\widehat {f}}}$ $${\displaystyle f(x)\ {\stackrel {\mathcal {F}}{\longleftrightarrow }}\ {\widehat {f}}(\xi ),}$$ ${\displaystyle \operatorname {rect} (x)\ {\stackrel {\mathcal {F}}{\longleftrightarrow }}\ \operatorname {sinc} (\xi ).}$

Definición de funciones integrables de Lebesgue

Hasta ahora, hemos estado tratando con funciones de Schwartz, que decaen rápidamente en el infinito, con todas las derivadas. Esto excluye muchas funciones de importancia práctica de la definición, como la función rect . Una función medible se llama (Lebesgue) integrable si la integral de Lebesgue de su valor absoluto es finita: Dos funciones mesurables son equivalentes si son iguales excepto en un conjunto de medida cero. El conjunto de todas las clases de equivalencia de funciones integrables se denota . Entonces: ^[11] ${\displaystyle f:\mathbb {R} \to \mathbb {C} }$ $${\displaystyle \|f\|_{1}=\int _{\mathbb {R} }|f(x)|\,dx<\infty .}$$ ${\displaystyle L^{1}(\mathbb {R} )}$

Definición  :  La transformada de Fourier de una función integrable de Lebesgue se define mediante la fórmula Eq.1 . ${\displaystyle f\in L^{1}(\mathbb {R} )}$

La ecuación integral 1 está bien definida para todos debido al supuesto . (Se puede demostrar que la función está acotada y es uniformemente continua en el dominio de la frecuencia y, además, por el lema de Riemann-Lebesgue , es cero en el infinito). ${\displaystyle \xi \in \mathbb {R} ,}$ ${\displaystyle \|f\|_{1}<\infty }$ ${\displaystyle {\widehat {f}}\in L^{\infty }\cap C(\mathbb {R} )}$

Sin embargo, la clase de funciones integrables de Lebesgue no es ideal desde el punto de vista de la transformada de Fourier porque no existe una caracterización fácil de la imagen y, por lo tanto, no existe una caracterización fácil de la transformada inversa.

Unitaridad y definición de funciones integrables al cuadrado

Si bien la ecuación 1 define la transformada de Fourier para funciones (de valores complejos) en , es fácil ver que no está bien definida para otras clases de integrabilidad, la más importante es . Para las funciones en , y con las convenciones de la ecuación 1 , la transformada de Fourier es un operador unitario con respecto al producto interno de Hilbert en , restringido al subespacio denso de funciones integrables. Por lo tanto, admite una extensión continua única a un operador unitario en , también llamado transformada de Fourier. Esta extensión es importante en parte porque la transformada de Fourier preserva el espacio de modo que, a diferencia del caso de , la transformada de Fourier y la transformada inversa están en el mismo pie de igualdad, siendo transformaciones del mismo espacio de funciones para sí mismo. ${\displaystyle L^{1}(\mathbb {R} )}$ ${\displaystyle L^{2}(\mathbb {R} )}$ ${\displaystyle L^{1}\cap L^{2}(\mathbb {R} )}$ ${\displaystyle L^{2}(\mathbb {R} )}$ ${\displaystyle L^{2}(\mathbb {R} )}$ ${\displaystyle L^{2}(\mathbb {R} )}$ ${\displaystyle L^{1}}$

Es importante destacar que, para las funciones en , la transformada de Fourier ya no está dada por la Ec.1 (interpretada como una integral de Lebesgue). Por ejemplo, la función está en pero no en , por lo que la integral Ec.1 diverge. En tales casos, la transformada de Fourier se puede obtener explícitamente regularizando la integral y luego pasándola a un límite. En la práctica, la integral a menudo se considera como una integral impropia en lugar de una integral de Lebesgue propia, pero a veces para la convergencia uno necesita usar un límite débil o un valor principal en lugar de los límites (puntuales) implícitos en una integral impropia. Titchmarsh (1986) y Dym & McKean (1985) dan cada uno tres formas rigurosas de extender la transformada de Fourier a funciones integrables al cuadrado usando este procedimiento. ${\displaystyle L^{2}}$ ${\displaystyle f(x)=(1+x^{2})^{-1/2}}$ ${\displaystyle L^{2}}$ ${\displaystyle L^{1}}$

Las convenciones elegidas en este artículo son las del análisis armónico , y se caracterizan como las únicas convenciones tales que la transformada de Fourier es a la vez unitaria en L ² y un homomorfismo algebraico de L ¹ a L ^∞ , sin renormalizar la medida de Lebesgue. ^[12]

Frecuencia angular (ω)

Cuando la variable independiente ( ) representa el tiempo (que suele denotarse con ), la variable de transformada ( ) representa la frecuencia (que suele denotarse con ). Por ejemplo, si el tiempo se mide en segundos , la frecuencia se mide en hercios . La transformada de Fourier también se puede escribir en términos de frecuencia angular , cuyas unidades son radianes por segundo. ${\displaystyle x}$ ${\displaystyle t}$ ${\displaystyle \xi }$ ${\displaystyle f}$ ${\displaystyle \omega =2\pi \xi ,}$

La sustitución en la ecuación 1 produce esta convención, donde la función se vuelve a etiquetar A diferencia de la definición de la ecuación 1 , la transformada de Fourier ya no es una transformación unitaria y hay menos simetría entre las fórmulas para la transformada y su inversa. Esas propiedades se restauran dividiendo el factor de manera uniforme entre la transformada y su inversa, lo que conduce a otra convención: Se pueden crear variaciones de las tres convenciones conjugando el núcleo exponencial complejo de la transformada directa y la inversa. Los signos deben ser opuestos. ${\displaystyle \xi ={\tfrac {\omega }{2\pi }}}$ ${\displaystyle {\widehat {f}}}$ ${\displaystyle {\widehat {f_{1}}}:}$ $${\displaystyle {\begin{aligned}{\widehat {f_{3}}}(\omega )&\triangleq \int _{-\infty }^{\infty }f(x)\cdot e^{-i\omega \,x}\,dx={\widehat {f_{1}}}\left({\tfrac {\omega }{2\pi }}\right),\\f(x)&={\frac {1}{2\pi }}\int _{-\infty }^{\infty }{\widehat {f_{3}}}(\omega )\cdot e^{i\omega \,x}\,d\omega .\end{aligned}}}$$ ${\displaystyle 2\pi }$ $${\displaystyle {\begin{aligned}{\widehat {f_{2}}}(\omega )&\triangleq {\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }f(x)\cdot e^{-i\omega x}\,dx={\frac {1}{\sqrt {2\pi }}}\cdot {\widehat {f_{1}}}\left({\tfrac {\omega }{2\pi }}\right),\\f(x)&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }{\widehat {f_{2}}}(\omega )\cdot e^{i\omega x}\,d\omega .\end{aligned}}}$$

Ampliación de la definición

Para , la transformada de Fourier se puede definir mediante la interpolación de Marcinkiewicz . ${\displaystyle 1<p<2}$ ${\displaystyle L^{p}(\mathbb {R} )}$

La transformada de Fourier se puede definir en dominios distintos de la línea real. La transformada de Fourier en el espacio euclidiano y la transformada de Fourier en grupos abelianos locales se analizan más adelante en este artículo.

La transformada de Fourier también se puede definir para distribuciones templadas , duales del espacio de funciones de decrecimiento rápido ( funciones de Schwartz ). Una función de Schwartz es una función suave que decae en el infinito, junto con todas sus derivadas. El espacio de funciones de Schwartz se denota por , y su dual es el espacio de distribuciones templadas. Es fácil ver, al derivar bajo la integral y aplicar el lema de Riemann-Lebesgue, que la transformada de Fourier de una función de Schwartz (definida por la fórmula Eq.1 ) es nuevamente una función de Schwartz. La transformada de Fourier de una distribución templada se define por dualidad: ${\displaystyle {\mathcal {S}}(\mathbb {R} )}$ ${\displaystyle {\mathcal {S}}'(\mathbb {R} )}$ ${\displaystyle T\in {\mathcal {S}}'(\mathbb {R} )}$ $${\displaystyle \langle {\widehat {T}},\phi \rangle =\langle T,{\widehat {\phi }}\rangle ;\quad \forall \phi \in {\mathcal {S}}(\mathbb {R} ).}$$

Existen muchas otras caracterizaciones de la transformada de Fourier. Por ejemplo, se utiliza el teorema de Stone-von Neumann : la transformada de Fourier es el único entrelazador unitario para las representaciones simpléctica y euclidiana de Schrödinger del grupo de Heisenberg .

Fondo

Historia

En 1822, Fourier afirmó (véase Joseph Fourier § La teoría analítica del calor ) que cualquier función, ya sea continua o discontinua, puede expandirse en una serie de senos. ^[13] Ese importante trabajo fue corregido y ampliado por otros para proporcionar la base para las diversas formas de la transformada de Fourier utilizadas desde entonces.

Fig.1 Cuando la función se representa en el plano complejo, el vector formado por sus partes imaginaria y real gira alrededor del origen. Su parte real es una onda coseno. ${\displaystyle A\cdot e^{i2\pi \xi t}}$ ${\displaystyle y(t)}$

Sinusoides complejos

En general, los coeficientes son números complejos, que tienen dos formas equivalentes (ver fórmula de Euler ): ${\displaystyle {\widehat {f}}(\xi )}$ $${\displaystyle {\widehat {f}}(\xi )=\underbrace {Ae^{i\theta }} _{\text{polar coordinate form}}=\underbrace {A\cos(\theta )+iA\sin(\theta )} _{\text{rectangular coordinate form}}.}$$

El producto con ( Eq.2 ) tiene estas formas: ${\displaystyle e^{i2\pi \xi x}}$ $${\displaystyle {\begin{aligned}{\widehat {f}}(\xi )\cdot e^{i2\pi \xi x}&=Ae^{i\theta }\cdot e^{i2\pi \xi x}\\&=\underbrace {Ae^{i(2\pi \xi x+\theta )}} _{\text{polar coordinate form}}\\&=\underbrace {A\cos(2\pi \xi x+\theta )+iA\sin(2\pi \xi x+\theta )} _{\text{rectangular coordinate form}}.\end{aligned}}}$$

Es de destacar la facilidad con la que se simplificó el producto utilizando la forma polar, y la facilidad con la que se dedujo la forma rectangular mediante una aplicación de la fórmula de Euler.

Frecuencia negativa

La fórmula de Euler introduce la posibilidad de negativa   Y la ecuación 1 está definida . Solo ciertas transformadas de valor complejo tienen transformadas (ver Señal analítica . Un ejemplo simple es ) Pero la frecuencia negativa es necesaria para caracterizar todas las demás transformadas de valor complejo que se encuentran en el procesamiento de señales , ecuaciones diferenciales parciales , radar , óptica no lineal , mecánica cuántica y otras. ${\displaystyle \xi .}$ ${\displaystyle \forall \xi \in \mathbb {R} .}$ ${\displaystyle f(x)}$ ${\displaystyle {\widehat {f}}=0,\ \forall \ \xi <0}$ ${\displaystyle e^{i2\pi \xi _{0}x}\ (\xi _{0}>0).}$ ${\displaystyle f(x),}$

Para una ecuación de valor real, la ecuación 1 tiene la propiedad de simetría (ver § Conjugación a continuación). Esta redundancia permite que la ecuación 2 se distinga de   Pero, por supuesto, no puede decirnos el signo real de porque y son indistinguibles solo en la línea de números reales. ${\displaystyle f(x),}$ ${\displaystyle {\widehat {f}}(-\xi )={\widehat {f}}^{*}(\xi )}$ ${\displaystyle f(x)=\cos(2\pi \xi _{0}x)}$ ${\displaystyle e^{i2\pi \xi _{0}x}.}$ ${\displaystyle \xi _{0},}$ ${\displaystyle \cos(2\pi \xi _{0}x)}$ ${\displaystyle \cos(2\pi (-\xi _{0})x)}$

Transformada de Fourier para funciones periódicas

La transformada de Fourier de una función periódica no se puede definir utilizando directamente la fórmula integral. Para que la integral en la ecuación 1 se defina, la función debe ser absolutamente integrable . En su lugar, es común utilizar series de Fourier . Es posible ampliar la definición para incluir funciones periódicas al considerarlas como distribuciones templadas .

Esto permite ver una conexión entre la serie de Fourier y la transformada de Fourier para funciones periódicas que tienen una serie de Fourier convergente . Si es una función periódica , con período , que tiene una serie de Fourier convergente, entonces: donde son los coeficientes de la serie de Fourier de , y es la función delta de Dirac . En otras palabras, la transformada de Fourier es una función de peine de Dirac cuyos dientes se multiplican por los coeficientes de la serie de Fourier. ${\displaystyle f(x)}$ ${\displaystyle P}$ $${\displaystyle {\widehat {f}}(\xi )=\sum _{n=-\infty }^{\infty }c_{n}\cdot \delta \left(\xi -{\tfrac {n}{P}}\right),}$$ ${\displaystyle c_{n}}$ ${\displaystyle f}$ ${\displaystyle \delta }$

Muestreo de la transformada de Fourier

La transformada de Fourier de una función integrable se puede muestrear a intervalos regulares de longitud arbitraria. Estas muestras se pueden deducir de un ciclo de una función periódica que tiene coeficientes de serie de Fourier proporcionales a esas muestras mediante la fórmula de suma de Poisson : ${\displaystyle f}$ ${\displaystyle {\tfrac {1}{P}}.}$ ${\displaystyle f_{P}}$ $${\displaystyle f_{P}(x)\triangleq \sum _{n=-\infty }^{\infty }f(x+nP)={\frac {1}{P}}\sum _{k=-\infty }^{\infty }{\widehat {f}}\left({\tfrac {k}{P}}\right)e^{i2\pi {\frac {k}{P}}x},\quad \forall k\in \mathbb {Z} }$$

La integrabilidad de garantiza la convergencia de la suma periódica. Por lo tanto, las muestras se pueden determinar mediante el análisis de series de Fourier: ${\displaystyle f}$ ${\displaystyle {\widehat {f}}\left({\tfrac {k}{P}}\right)}$ $${\displaystyle {\widehat {f}}\left({\tfrac {k}{P}}\right)=\int _{P}f_{P}(x)\cdot e^{-i2\pi {\frac {k}{P}}x}\,dx.}$$

Cuando tiene un soporte compacto , tiene un número finito de términos dentro del intervalo de integración. Cuando no tiene un soporte compacto, la evaluación numérica de requiere una aproximación, como reducir o truncar el número de términos. ${\displaystyle f(x)}$ ${\displaystyle f_{P}(x)}$ ${\displaystyle f(x)}$ ${\displaystyle f_{P}(x)}$ ${\displaystyle f(x)}$

Ejemplo

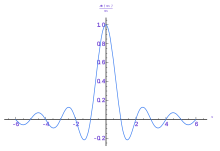
Las siguientes figuras proporcionan una ilustración visual de cómo la integral de la transformada de Fourier mide si una frecuencia está presente en una función particular. La primera imagen representa la función que es una onda coseno de 3  Hz (el primer término) formada por una función envolvente gaussiana (el segundo término) que enciende y apaga suavemente la onda. Las siguientes 2 imágenes muestran el producto que debe integrarse para calcular la transformada de Fourier a +3 Hz. La parte real del integrando tiene un valor promedio no negativo, porque los signos alternos de y oscilan a la misma velocidad y en fase, mientras que y oscilan a la misma velocidad pero con fase ortogonal. El valor absoluto de la transformada de Fourier a +3 Hz es 0,5, que es relativamente grande. Cuando se suma a la transformada de Fourier a -3 Hz (que es idéntica porque comenzamos con una señal real), encontramos que la amplitud del componente de frecuencia de 3 Hz es 1. ${\displaystyle f(t)=\cos(2\pi \ 3t)\ e^{-\pi t^{2}},}$ ${\displaystyle f(t)e^{-i2\pi 3t},}$ ${\displaystyle f(t)}$ ${\displaystyle \operatorname {Re} (e^{-i2\pi 3t})}$ ${\displaystyle f(t)}$ ${\displaystyle \operatorname {Im} (e^{-i2\pi 3t})}$

Función original, que tiene un fuerte componente de 3 Hz. Partes real e imaginaria del integrando de su transformada de Fourier a +3 Hz.

Sin embargo, cuando se intenta medir una frecuencia que no está presente, tanto el componente real como el imaginario de la integral varían rápidamente entre valores positivos y negativos. Por ejemplo, la curva roja busca 5 Hz. El valor absoluto de su integral es casi cero, lo que indica que casi no había ningún componente de 5 Hz en la señal. La situación general suele ser más complicada que esto, pero heurísticamente así es como la transformada de Fourier mide qué cantidad de una frecuencia individual está presente en una función. ${\displaystyle f(t).}$

• 
  Partes reales e imaginarias del integrando para su transformada de Fourier a +5 Hz.
• 
  Magnitud de su transformada de Fourier, con +3 y +5 Hz etiquetados.

Para reforzar un punto anterior, la razón de la respuesta en   Hz es que     y     son indistinguibles. La transformada de     tendría solo una respuesta, cuya amplitud es la integral de la envolvente suave:   mientras   que es   ${\displaystyle \xi =-3}$ ${\displaystyle \cos(2\pi 3t)}$ ${\displaystyle \cos(2\pi (-3)t)}$ ${\displaystyle e^{i2\pi 3t}\cdot e^{-\pi t^{2}}}$ ${\displaystyle e^{-\pi t^{2}},}$ ${\displaystyle \operatorname {Re} (f(t)\cdot e^{-i2\pi 3t})}$ ${\displaystyle e^{-\pi t^{2}}(1+\cos(2\pi 6t))/2.}$

Propiedades de la transformada de Fourier

Sean y representen funciones integrables Lebesgue-medibles en la recta real que satisfacen: Denotamos las transformadas de Fourier de estas funciones como y respectivamente. ${\displaystyle f(x)}$ ${\displaystyle h(x)}$ $${\displaystyle \int _{-\infty }^{\infty }|f(x)|\,dx<\infty .}$$ ${\displaystyle {\hat {f}}(\xi )}$ ${\displaystyle {\hat {h}}(\xi )}$

Propiedades básicas

La transformada de Fourier tiene las siguientes propiedades básicas: ^[14]

Linealidad

$${\displaystyle a\ f(x)+b\ h(x)\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ a\ {\widehat {f}}(\xi )+b\ {\widehat {h}}(\xi );\quad \ a,b\in \mathbb {C} }$$

Cambio de hora

$${\displaystyle f(x-x_{0})\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ e^{-i2\pi x_{0}\xi }\ {\widehat {f}}(\xi );\quad \ x_{0}\in \mathbb {R} }$$

Cambio de frecuencia

$${\displaystyle e^{i2\pi \xi _{0}x}f(x)\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ {\widehat {f}}(\xi -\xi _{0});\quad \ \xi _{0}\in \mathbb {R} }$$

Escala de tiempo

$${\displaystyle f(ax)\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ {\frac {1}{|a|}}{\widehat {f}}\left({\frac {\xi }{a}}\right);\quad \ a\neq 0}$$El caso conduce a la propiedad de inversión temporal : ${\displaystyle a=-1}$ $${\displaystyle f(-x)\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ {\widehat {f}}(-\xi )}$$

Simetría

Cuando las partes reales e imaginarias de una función compleja se descomponen en sus partes pares e impares , hay cuatro componentes, denotados a continuación por los subíndices RE, RO, IE e IO. Y hay una correspondencia uno a uno entre los cuatro componentes de una función de tiempo compleja y los cuatro componentes de su transformada de frecuencia compleja: $${\displaystyle {\begin{aligned}{\mathsf {Time\ domain}}\quad &\ f\quad &=\quad &f_{_{RE}}\quad &+\quad &f_{_{RO}}\quad &+\quad i\ &f_{_{IE}}\quad &+\quad &\underbrace {i\ f_{_{IO}}} \\&{\Bigg \Updownarrow }{\mathcal {F}}&&{\Bigg \Updownarrow }{\mathcal {F}}&&\ \ {\Bigg \Updownarrow }{\mathcal {F}}&&\ \ {\Bigg \Updownarrow }{\mathcal {F}}&&\ \ {\Bigg \Updownarrow }{\mathcal {F}}\\{\mathsf {Frequency\ domain}}\quad &{\widehat {f}}\quad &=\quad &{\widehat {f}}_{RE}\quad &+\quad &\overbrace {i\ {\widehat {f}}_{IO}} \quad &+\quad i\ &{\widehat {f}}_{IE}\quad &+\quad &{\widehat {f}}_{RO}\end{aligned}}}$$

De esto se desprenden diversas relaciones, por ejemplo :

• La transformada de una función de valor real es la función simétrica conjugada . Por el contrario, una transformada simétrica conjugada implica un dominio de tiempo de valor real. ${\displaystyle (f_{_{RE}}+f_{_{RO}})}$ ${\displaystyle {\hat {f}}_{RE}+i\ {\hat {f}}_{IO}.}$
• La transformada de una función de valor imaginario es la función antisimétrica conjugada y la inversa es verdadera. ${\displaystyle (i\ f_{_{IE}}+i\ f_{_{IO}})}$ ${\displaystyle {\hat {f}}_{RO}+i\ {\hat {f}}_{IE},}$
• La transformada de una función simétrica conjugada es la función de valor real y la inversa es verdadera. ${\displaystyle (f_{_{RE}}+i\ f_{_{IO}})}$ ${\displaystyle {\hat {f}}_{RE}+{\hat {f}}_{RO},}$
• La transformada de una función antisimétrica conjugada es la función de valor imaginario y la inversa es verdadera. ${\displaystyle (f_{_{RO}}+i\ f_{_{IE}})}$ ${\displaystyle i\ {\hat {f}}_{IE}+i{\hat {f}}_{IO},}$

Conjugación

$${\displaystyle {\bigl (}f(x){\bigr )}^{*}\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ \left({\widehat {f}}(-\xi )\right)^{*}}$$(Nota: el ∗ denota conjugación compleja ).

En particular, si es real , entonces es incluso simétrica (también conocida como función hermítica ): ${\displaystyle f}$ ${\displaystyle {\widehat {f}}}$ $${\displaystyle {\widehat {f}}(-\xi )={\bigl (}{\widehat {f}}(\xi ){\bigr )}^{*}.}$$

Y si es puramente imaginario, entonces es impar simétrico : ${\displaystyle f}$ ${\displaystyle {\widehat {f}}}$ $${\displaystyle {\widehat {f}}(-\xi )=-({\widehat {f}}(\xi ))^{*}.}$$

Parte real e imaginaria del tiempo

$${\displaystyle \operatorname {Re} \{f(x)\}\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ {\tfrac {1}{2}}\left({\widehat {f}}(\xi )+{\bigl (}{\widehat {f}}(-\xi ){\bigr )}^{*}\right)}$$ $${\displaystyle \operatorname {Im} \{f(x)\}\ \ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ {\tfrac {1}{2i}}\left({\widehat {f}}(\xi )-{\bigl (}{\widehat {f}}(-\xi ){\bigr )}^{*}\right)}$$

Componente de frecuencia cero

Sustituyendo en la definición, obtenemos: ${\displaystyle \xi =0}$ $${\displaystyle {\widehat {f}}(0)=\int _{-\infty }^{\infty }f(x)\,dx.}$$

La integral de sobre su dominio se conoce como valor promedio o polarización continua de la función. ${\displaystyle f}$

Invertibilidad y periodicidad

En condiciones adecuadas en la función , se puede recuperar a partir de su transformada de Fourier . De hecho, denotando el operador de transformada de Fourier por , por lo que , entonces para funciones adecuadas, aplicar la transformada de Fourier dos veces simplemente invierte la función: , que puede interpretarse como "tiempo invertido". Dado que el tiempo invertido es biperiódico, aplicar esto dos veces produce , por lo que el operador de transformada de Fourier es cuatroperiódico, y de manera similar, la transformada de Fourier inversa se puede obtener aplicando la transformada de Fourier tres veces: . En particular, la transformada de Fourier es invertible (en condiciones adecuadas). ${\displaystyle f}$ ${\displaystyle {\hat {f}}}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}f:={\hat {f}}}$ ${\displaystyle \left({\mathcal {F}}^{2}f\right)(x)=f(-x)}$ ${\displaystyle {\mathcal {F}}^{4}(f)=f}$ ${\displaystyle {\mathcal {F}}^{3}\left({\hat {f}}\right)=f}$

Más precisamente, definiendo el operador de paridad tal que , tenemos: Estas igualdades de operadores requieren una definición cuidadosa del espacio de funciones en cuestión, definiendo la igualdad de funciones (¿igualdad en cada punto? ¿igualdad casi en todas partes ?) y definiendo la igualdad de operadores – es decir, definiendo la topología en el espacio de funciones y el espacio de operadores en cuestión. Estas no son verdaderas para todas las funciones, pero son verdaderas bajo varias condiciones, que son el contenido de las varias formas del teorema de inversión de Fourier . ${\displaystyle {\mathcal {P}}}$ ${\displaystyle ({\mathcal {P}}f)(x)=f(-x)}$ $${\displaystyle {\begin{aligned}{\mathcal {F}}^{0}&=\mathrm {id} ,\\{\mathcal {F}}^{1}&={\mathcal {F}},\\{\mathcal {F}}^{2}&={\mathcal {P}},\\{\mathcal {F}}^{3}&={\mathcal {F}}^{-1}={\mathcal {P}}\circ {\mathcal {F}}={\mathcal {F}}\circ {\mathcal {P}},\\{\mathcal {F}}^{4}&=\mathrm {id} \end{aligned}}}$$

Esta periodicidad cuádruple de la transformada de Fourier es similar a una rotación del plano de 90°, particularmente porque la iteración doble produce una inversión, y de hecho esta analogía se puede hacer precisa. Mientras que la transformada de Fourier se puede interpretar simplemente como cambiar el dominio del tiempo y el dominio de la frecuencia, con la transformada de Fourier inversa cambiándolos de nuevo, más geométricamente se puede interpretar como una rotación de 90° en el dominio del tiempo-frecuencia (considerando el tiempo como el eje x y la frecuencia como el eje y ), y la transformada de Fourier se puede generalizar a la transformada de Fourier fraccionaria , que implica rotaciones de otros ángulos. Esto se puede generalizar aún más a las transformaciones canónicas lineales , que se pueden visualizar como la acción del grupo lineal especial SL ₂ ( R ) en el plano de tiempo-frecuencia, con la forma simpléctica preservada correspondiente al principio de incertidumbre, a continuación. Este enfoque se estudia particularmente en el procesamiento de señales , en el análisis de tiempo-frecuencia .

Unidades

La variable de frecuencia debe tener unidades inversas a las unidades del dominio de la función original (normalmente denominadas t o x ). Por ejemplo, si t se mide en segundos, ξ debería estar en ciclos por segundo o hercios . Si la escala de tiempo está en unidades de 2 π segundos, normalmente se utiliza otra letra griega ω para representar la frecuencia angular (donde ω = 2π ξ ) en unidades de radianes por segundo. Si se utiliza x para unidades de longitud, entonces ξ debe estar en longitud inversa, por ejemplo, números de onda . Es decir, hay dos versiones de la línea real: una que es el rango de t y se mide en unidades de t , y la otra que es el rango de ξ y se mide en unidades inversas a las unidades de t . Estas dos versiones distintas de la línea real no se pueden equiparar entre sí. Por tanto, la transformada de Fourier va de un espacio de funciones a un espacio de funciones diferente: funciones que tienen un dominio de definición diferente.

En general, ξ debe tomarse siempre como una forma lineal en el espacio de su dominio, es decir, que la segunda recta real es el espacio dual de la primera recta real. Véase el artículo sobre álgebra lineal para una explicación más formal y para más detalles. Este punto de vista se vuelve esencial en las generalizaciones de la transformada de Fourier a grupos de simetría generales , incluido el caso de las series de Fourier.

El hecho de que no exista una única forma preferida (a menudo se dice "ninguna forma canónica") de comparar las dos versiones de la línea real que intervienen en la transformada de Fourier (fijar las unidades en una línea no fuerza la escala de las unidades en la otra) es la razón de la plétora de convenciones rivales sobre la definición de la transformada de Fourier. Las diversas definiciones resultantes de las distintas opciones de unidades difieren en varias constantes.

En otras convenciones, la transformada de Fourier tiene i en el exponente en lugar de − i , y viceversa para la fórmula de inversión. Esta convención es común en la física moderna ^[15] y es la predeterminada para Wolfram Alpha, y no significa que la frecuencia se haya vuelto negativa, ya que no existe una definición canónica de positividad para la frecuencia de una onda compleja. Simplemente significa que es la amplitud de la onda     en lugar de la onda   (la primera, con su signo menos, se ve a menudo en la dependencia del tiempo para soluciones de ondas planas sinusoidales de la ecuación de onda electromagnética , o en la dependencia del tiempo para funciones de onda cuántica ). Muchas de las identidades que involucran la transformada de Fourier siguen siendo válidas en esas convenciones, siempre que todos los términos que involucran explícitamente i lo tengan reemplazado por − i . En ingeniería eléctrica, la letra j se usa típicamente para la unidad imaginaria en lugar de i porque i se usa para corriente. ${\displaystyle {\hat {f}}(\xi )}$ ${\displaystyle e^{-i2\pi \xi x}}$ ${\displaystyle e^{i2\pi \xi x}}$

Cuando se utilizan unidades adimensionales , los factores constantes podrían ni siquiera estar escritos en la definición de la transformada. Por ejemplo, en teoría de la probabilidad , la función característica Φ de la función de densidad de probabilidad f de una variable aleatoria X de tipo continuo se define sin un signo negativo en la exponencial, y como las unidades de x se ignoran, tampoco hay 2 π : $${\displaystyle \phi (\lambda )=\int _{-\infty }^{\infty }f(x)e^{i\lambda x}\,dx.}$$

(En teoría de probabilidad y en estadística matemática, se prefiere el uso de la transformada de Fourier-Stieltjes, porque muchas variables aleatorias no son de tipo continuo y no poseen una función de densidad, y uno debe tratar no funciones sino distribuciones , es decir, medidas que poseen "átomos".)

Desde el punto de vista más elevado de los caracteres de grupo , que es mucho más abstracto, todas estas elecciones arbitrarias desaparecen, como se explicará en la sección posterior de este artículo, que trata la noción de transformada de Fourier de una función en un grupo abeliano localmente compacto .

Continuidad uniforme y el lema de Riemann-Lebesgue

La función rectangular es integrable según Lebesgue .

La función sinc , que es la transformada de Fourier de la función rectangular, es acotada y continua, pero no integrable según el método de Lebesgue.

La transformada de Fourier puede definirse en algunos casos para funciones no integrables, pero las transformadas de Fourier de funciones integrables tienen varias propiedades importantes.

La transformada de Fourier f̂ de cualquier función integrable f es uniformemente continua y ^[16] $${\displaystyle \left\|{\hat {f}}\right\|_{\infty }\leq \left\|f\right\|_{1}}$$

Por el lema de Riemann-Lebesgue , ^[11] $${\displaystyle {\hat {f}}(\xi )\to 0{\text{ as }}|\xi |\to \infty .}$$

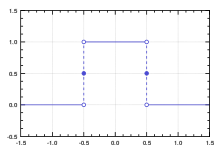
Sin embargo, no es necesario que sean integrables. Por ejemplo, la transformada de Fourier de la función rectangular , que es integrable, es la función sinc , que no es integrable según el método de Lebesgue , porque sus integrales impropias se comportan de manera análoga a las series armónicas alternas , al converger a una suma sin ser absolutamente convergentes . ${\displaystyle {\hat {f}}}$

En general, no es posible escribir la transformada inversa como una integral de Lebesgue . Sin embargo, cuando tanto f como son integrables, la igualdad inversa se cumple para casi todo x . Como resultado, la transformada de Fourier es inyectiva en L 1 ( R ) . ${\displaystyle {\hat {f}}}$ $${\displaystyle f(x)=\int _{-\infty }^{\infty }{\hat {f}}(\xi )e^{i2\pi x\xi }\,d\xi }$$

Teorema de Plancherel y teorema de Parseval

Página principal: Teorema de Plancherel

Sean f ( x ) y g ( x ) integrables, y sean f̂ ( ξ ) y ĝ ( ξ ) sus transformadas de Fourier. Si f ( x ) y g ( x ) también son integrables al cuadrado , entonces la fórmula de Parseval es la siguiente: ^[17]

$${\displaystyle \langle f,g\rangle _{L^{2}}=\int _{-\infty }^{\infty }f(x){\overline {g(x)}}\,dx=\int _{-\infty }^{\infty }{\hat {f}}(\xi ){\overline {{\hat {g}}(\xi )}}\,d\xi ,}$$donde la barra denota conjugación compleja .

El teorema de Plancherel , que se desprende de lo anterior, establece que ^[18] $${\displaystyle \|f\|_{L^{2}}^{2}=\int _{-\infty }^{\infty }\left|f(x)\right|^{2}\,dx=\int _{-\infty }^{\infty }\left|{\hat {f}}(\xi )\right|^{2}\,d\xi .}$$

El teorema de Plancherel permite extender la transformada de Fourier, mediante un argumento de continuidad, a un operador unitario en L ² ( R ) . En L ¹ ( R ) ∩ L ² ( R ) , esta extensión concuerda con la transformada de Fourier original definida en L ¹ ( R ) , ampliando así el dominio de la transformada de Fourier a L ¹ ( R ) + L ² ( R ) (y en consecuencia a L ^p ( R ) para 1 ≤ p ≤ 2 ). El teorema de Plancherel tiene la interpretación en las ciencias de que la transformada de Fourier preserva la energía de la cantidad original. La terminología de estas fórmulas no está del todo estandarizada. El teorema de Parseval se demostró solo para series de Fourier, y fue demostrado por primera vez por Lyapunov. Pero la fórmula de Parseval también tiene sentido para la transformada de Fourier, y aunque en el contexto de la transformada de Fourier fue demostrada por Plancherel, todavía se suele hacer referencia a ella como la fórmula de Parseval, o la relación de Parseval, o incluso el teorema de Parseval.

Véase la dualidad de Pontryagin para una formulación general de este concepto en el contexto de grupos abelianos localmente compactos.

Fórmula de suma de Poisson

La fórmula de suma de Poisson (PSF) es una ecuación que relaciona los coeficientes de la serie de Fourier de la suma periódica de una función con los valores de la transformada de Fourier continua de la función. La fórmula de suma de Poisson dice que para funciones suficientemente regulares f , $${\displaystyle \sum _{n}{\hat {f}}(n)=\sum _{n}f(n).}$$

Tiene una variedad de formas útiles que se derivan de la básica mediante la aplicación de las propiedades de escala y desplazamiento temporal de la transformada de Fourier. La fórmula tiene aplicaciones en ingeniería, física y teoría de números . El dual en el dominio de la frecuencia de la fórmula de suma de Poisson estándar también se denomina transformada de Fourier de tiempo discreto .

La suma de Poisson se asocia generalmente con la física de los medios periódicos, como la conducción de calor en un círculo. La solución fundamental de la ecuación del calor en un círculo se llama función theta . Se utiliza en la teoría de números para demostrar las propiedades de transformación de las funciones theta, que resultan ser un tipo de forma modular , y está conectada de manera más general con la teoría de las formas automórficas donde aparece en un lado de la fórmula de traza de Selberg .

Diferenciación

Supóngase que f ( x ) es una función diferenciable absolutamente continua, y tanto f como su derivada f′ son integrables. Entonces la transformada de Fourier de la derivada está dada por De manera más general, la transformada de Fourier de la n ésima derivada f ^{( n )} está dada por $${\displaystyle {\widehat {f'\,}}(\xi )={\mathcal {F}}\left\{{\frac {d}{dx}}f(x)\right\}=i2\pi \xi {\hat {f}}(\xi ).}$$ $${\displaystyle {\widehat {f^{(n)}}}(\xi )={\mathcal {F}}\left\{{\frac {d^{n}}{dx^{n}}}f(x)\right\}=(i2\pi \xi )^{n}{\hat {f}}(\xi ).}$$

Análogamente, , por lo que ${\displaystyle {\mathcal {F}}\left\{{\frac {d^{n}}{d\xi ^{n}}}{\hat {f}}(\xi )\right\}=(i2\pi x)^{n}f(x)}$ ${\displaystyle {\mathcal {F}}\left\{x^{n}f(x)\right\}=\left({\frac {i}{2\pi }}\right)^{n}{\frac {d^{n}}{d\xi ^{n}}}{\hat {f}}(\xi ).}$

Aplicando la transformada de Fourier y utilizando estas fórmulas, algunas ecuaciones diferenciales ordinarias pueden transformarse en ecuaciones algebraicas, que son mucho más fáciles de resolver. Estas fórmulas también dan lugar a la regla general " f ( x ) es suave si y solo si f̂ ( ξ ) cae rápidamente a 0 para | ξ | → ∞ ." Utilizando las reglas análogas para la transformada de Fourier inversa, también se puede decir " f ( x ) cae rápidamente a 0 para | x | → ∞ si y solo si f̂ ( ξ ) es suave."

Teorema de convolución

La transformada de Fourier se traduce entre convolución y multiplicación de funciones. Si f ( x ) y g ( x ) son funciones integrables con transformadas de Fourier f̂ ( ξ ) y ĝ ( ξ ) respectivamente, entonces la transformada de Fourier de la convolución viene dada por el producto de las transformadas de Fourier f̂ ( ξ ) y ĝ ( ξ ) (bajo otras convenciones para la definición de la transformada de Fourier puede aparecer un factor constante).

Esto significa que si: donde ∗ denota la operación de convolución, entonces: $${\displaystyle h(x)=(f*g)(x)=\int _{-\infty }^{\infty }f(y)g(x-y)\,dy,}$$ $${\displaystyle {\hat {h}}(\xi )={\hat {f}}(\xi )\,{\hat {g}}(\xi ).}$$

En la teoría de sistemas lineales invariantes en el tiempo (LTI) , es común interpretar g ( x ) como la respuesta al impulso de un sistema LTI con entrada f ( x ) y salida h ( x ) , ya que al sustituir el impulso unitario por f ( x ) se obtiene h ( x ) = g ( x ) . En este caso, ĝ ( ξ ) representa la respuesta en frecuencia del sistema.

Por el contrario, si f ( x ) puede descomponerse como el producto de dos funciones integrables al cuadrado p ( x ) y q ( x ) , entonces la transformada de Fourier de f ( x ) está dada por la convolución de las respectivas transformadas de Fourier p̂ ( ξ ) y q̂ ( ξ ) .

Teorema de correlación cruzada

De manera análoga, se puede demostrar que si h ( x ) es la correlación cruzada de f ( x ) y g ( x ) : entonces la transformada de Fourier de h ( x ) es: $${\displaystyle h(x)=(f\star g)(x)=\int _{-\infty }^{\infty }{\overline {f(y)}}g(x+y)\,dy}$$ $${\displaystyle {\hat {h}}(\xi )={\overline {{\hat {f}}(\xi )}}\,{\hat {g}}(\xi ).}$$

Como caso especial, la autocorrelación de la función f ( x ) es: para lo cual $${\displaystyle h(x)=(f\star f)(x)=\int _{-\infty }^{\infty }{\overline {f(y)}}f(x+y)\,dy}$$ $${\displaystyle {\hat {h}}(\xi )={\overline {{\hat {f}}(\xi )}}{\hat {f}}(\xi )=\left|{\hat {f}}(\xi )\right|^{2}.}$$

Funciones propias

La transformada de Fourier es una transformada lineal que tiene funciones propias que obedecen a ${\displaystyle {\mathcal {F}}[\psi ]=\lambda \psi ,}$ ${\displaystyle \lambda \in \mathbb {C} .}$

Un conjunto de funciones propias se encuentra al notar que la ecuación diferencial homogénea conduce a funciones propias de la transformada de Fourier siempre que la forma de la ecuación permanezca invariable bajo la transformada de Fourier. ^{[nota 5]} En otras palabras, cada solución y su transformada de Fourier obedecen a la misma ecuación. Suponiendo unicidad de las soluciones, cada solución debe ser, por lo tanto, una función propia de la transformada de Fourier. La forma de la ecuación permanece invariable bajo la transformada de Fourier si se puede expandir en una serie de potencias en la que para todos los términos el mismo factor de cualquiera de los dos surge de los factores introducidos por las reglas de diferenciación al transformar la ecuación diferencial homogénea de Fourier porque este factor puede entonces cancelarse. La opción más simple permitida conduce a la distribución normal estándar . ^[19] $${\displaystyle \left[U\left({\frac {1}{2\pi }}{\frac {d}{dx}}\right)+U(x)\right]\psi (x)=0}$$ ${\displaystyle \psi (x)}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle \psi (x)}$ ${\displaystyle {\hat {\psi }}(\xi )}$ ${\displaystyle \psi (x)}$ ${\displaystyle U(x)}$ ${\displaystyle \pm 1,\pm i}$ ${\displaystyle i^{n}}$ ${\displaystyle U(x)=x}$

De manera más general, también se encuentra un conjunto de funciones propias observando que las reglas de diferenciación implican que la ecuación diferencial ordinaria con constantes y siendo una función par no constante permanece invariante en forma al aplicar la transformada de Fourier a ambos lados de la ecuación. El ejemplo más simple lo proporciona que es equivalente a considerar la ecuación de Schrödinger para el oscilador armónico cuántico . ^[20] Las soluciones correspondientes proporcionan una elección importante de una base ortonormal para L 2 ( R ) y están dadas por las funciones de Hermite del "físico" . De manera equivalente, se puede utilizar donde He _n ( x ) son los polinomios de Hermite del "probabilista" , definidos como $${\displaystyle \left[W\left({\frac {i}{2\pi }}{\frac {d}{dx}}\right)+W(x)\right]\psi (x)=C\psi (x)}$$ ${\displaystyle C}$ ${\displaystyle W(x)}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle W(x)=x^{2}}$ $${\displaystyle \psi _{n}(x)={\frac {\sqrt[{4}]{2}}{\sqrt {n!}}}e^{-\pi x^{2}}\mathrm {He} _{n}\left(2x{\sqrt {\pi }}\right),}$$ $${\displaystyle \mathrm {He} _{n}(x)=(-1)^{n}e^{{\frac {1}{2}}x^{2}}\left({\frac {d}{dx}}\right)^{n}e^{-{\frac {1}{2}}x^{2}}.}$$

Bajo esta convención para la transformada de Fourier, tenemos que $${\displaystyle {\hat {\psi }}_{n}(\xi )=(-i)^{n}\psi _{n}(\xi ).}$$

En otras palabras, las funciones de Hermite forman un sistema ortonormal completo de funciones propias para la transformada de Fourier en L ² ( R ) . ^{[14] [21]} Sin embargo, esta elección de funciones propias no es única. Debido a que solo hay cuatro valores propios diferentes de la transformada de Fourier (las raíces cuartas de la unidad ±1 y ± i ) y cualquier combinación lineal de funciones propias con el mismo valor propio da otra función propia. ^[22] Como consecuencia de esto, es posible descomponer L ² ( R ) como una suma directa de cuatro espacios H ₀ , H ₁ , H ₂ y H ₃ donde la transformada de Fourier actúa sobre He _k simplemente por multiplicación por i ^k . ${\displaystyle {\mathcal {F}}^{4}=\mathrm {id} }$

Dado que el conjunto completo de funciones de Hermite ψ _n proporciona una resolución de la identidad, diagonalizan el operador de Fourier, es decir, la transformada de Fourier se puede representar mediante una suma de términos ponderada por los valores propios anteriores, y estas sumas se pueden sumar explícitamente: $${\displaystyle {\mathcal {F}}[f](\xi )=\int dxf(x)\sum _{n\geq 0}(-i)^{n}\psi _{n}(x)\psi _{n}(\xi )~.}$$

Este enfoque para definir la transformada de Fourier fue propuesto por primera vez por Norbert Wiener . ^[23] Entre otras propiedades, las funciones de Hermite decrecen exponencialmente rápido tanto en el dominio de la frecuencia como en el del tiempo, y por lo tanto se utilizan para definir una generalización de la transformada de Fourier, a saber, la transformada de Fourier fraccionaria utilizada en el análisis de tiempo-frecuencia. ^[24] En física , esta transformada fue introducida por Edward Condon . ^[25] Este cambio de funciones de base se hace posible porque la transformada de Fourier es una transformada unitaria cuando se utilizan las convenciones correctas. En consecuencia, bajo las condiciones adecuadas se puede esperar que resulte de un generador autoadjunto a través de ^[26] ${\displaystyle N}$ $${\displaystyle {\mathcal {F}}[\psi ]=e^{-itN}\psi .}$$

El operador es el operador numérico del oscilador armónico cuántico escrito como ^{[27] [28]} ${\displaystyle N}$ $${\displaystyle N\equiv {\frac {1}{2}}\left(x-{\frac {\partial }{\partial x}}\right)\left(x+{\frac {\partial }{\partial x}}\right)={\frac {1}{2}}\left(-{\frac {\partial ^{2}}{\partial x^{2}}}+x^{2}-1\right).}$$

Puede interpretarse como el generador de transformadas de Fourier fraccionarias para valores arbitrarios de t , y de la transformada de Fourier continua convencional para el valor particular con el núcleo de Mehler implementando la transformada activa correspondiente . Las funciones propias de son las funciones de Hermite que, por lo tanto, también son funciones propias de ${\displaystyle {\mathcal {F}}}$ ${\displaystyle t=\pi /2,}$ ${\displaystyle N}$ ${\displaystyle \psi _{n}(x)}$ ${\displaystyle {\mathcal {F}}.}$

Al extender la transformada de Fourier a las distribuciones, el peine de Dirac también es una función propia de la transformada de Fourier.

Conexión con el grupo de Heisenberg

El grupo de Heisenberg es un grupo determinado de operadores unitarios en el espacio de Hilbert L ² ( R ) de funciones complejas integrables al cuadrado f en la recta real, generadas por las traslaciones ( T _y f )( x ) = f ( x + y ) y la multiplicación por e ^{i 2π ξx} , ( M _ξ f )( x ) = e ^{i 2π ξx} f ( x ) . Estos operadores no conmutan, ya que su conmutador (de grupo) es que es la multiplicación por la constante (independiente de x ) e ^{i 2π ξy} ∈ U (1) (el grupo circular de números complejos de módulo unitario). Como grupo abstracto, el grupo de Heisenberg es el grupo de Lie tridimensional de ternas ( x , ξ , z ) ∈ R ² × U (1) , con la ley de grupo $${\displaystyle \left(M_{\xi }^{-1}T_{y}^{-1}M_{\xi }T_{y}f\right)(x)=e^{i2\pi \xi y}f(x)}$$ $${\displaystyle \left(x_{1},\xi _{1},t_{1}\right)\cdot \left(x_{2},\xi _{2},t_{2}\right)=\left(x_{1}+x_{2},\xi _{1}+\xi _{2},t_{1}t_{2}e^{i2\pi \left(x_{1}\xi _{1}+x_{2}\xi _{2}+x_{1}\xi _{2}\right)}\right).}$$

Denotemos el grupo de Heisenberg por H ₁ . El procedimiento anterior describe no solo la estructura del grupo, sino también una representación unitaria estándar de H ₁ en un espacio de Hilbert, que denotamos por ρ  : H ₁ → B ( L ² ( R )) . Definamos el automorfismo lineal de R ² por de modo que J ² = − I . Esta J se puede extender a un automorfismo único de H ₁ : $${\displaystyle J{\begin{pmatrix}x\\\xi \end{pmatrix}}={\begin{pmatrix}-\xi \\x\end{pmatrix}}}$$ $${\displaystyle j\left(x,\xi ,t\right)=\left(-\xi ,x,te^{-i2\pi \xi x}\right).}$$

Según el teorema de Stone-von Neumann , las representaciones unitarias ρ y ρ ∘ j son unitariamente equivalentes, por lo que existe un entrelazador único W ∈ U ( L ² ( R )) tal que Este operador W es la transformada de Fourier. $${\displaystyle \rho \circ j=W\rho W^{*}.}$$

Muchas de las propiedades estándar de la transformada de Fourier son consecuencias inmediatas de este marco más general. ^[29] Por ejemplo, el cuadrado de la transformada de Fourier, W ² , es un entrelazador asociado con J ² = − I , y por lo tanto tenemos que ( W ² f )( x ) = f (− x ) es el reflejo de la función original f .

Dominio complejo

La integral de la transformada de Fourier se puede estudiar para valores complejos de su argumento ξ . Dependiendo de las propiedades de f , es posible que no converja fuera del eje real en absoluto, o que converja a una función analítica compleja para todos los valores de ξ = σ + iτ , o algo intermedio. ^[30] $${\displaystyle {\hat {f}}(\xi )=\int _{-\infty }^{\infty }e^{-i2\pi \xi t}f(t)\,dt}$$

El teorema de Paley-Wiener dice que f es suave (es decir, n veces diferenciable para todos los enteros positivos n ) y con soporte compacto si y solo si f̂ ( σ + iτ ) es una función holomorfa para la que existe una constante a > 0 tal que para cualquier entero n ≥ 0 , para alguna constante C . (En este caso, f se soporta en [− a , a ] .) Esto se puede expresar diciendo que f̂ es una función entera que es rápidamente decreciente en σ (para τ fijo ) y de crecimiento exponencial en τ (uniformemente en σ ). ^[31] $${\displaystyle \left\vert \xi ^{n}{\hat {f}}(\xi )\right\vert \leq Ce^{a\vert \tau \vert }}$$

(Si f no es suave, sino solo L ² , la afirmación sigue siendo válida siempre que n = 0 . ^[32] ) El espacio de tales funciones de una variable compleja se denomina espacio de Paley-Wiener. Este teorema se ha generalizado a grupos de Lie semisimples . ^[33]

Si f se apoya en la semirrecta t ≥ 0 , entonces se dice que f es "causal" porque la función de respuesta al impulso de un filtro físicamente realizable debe tener esta propiedad, ya que ningún efecto puede preceder a su causa. Paley y Wiener demostraron que entonces f̂ se extiende a una función holomorfa en el semiplano inferior complejo τ < 0 que tiende a cero cuando τ tiende a infinito. ^[34] La inversa es falsa y no se sabe cómo caracterizar la transformada de Fourier de una función causal. ^[35]

Transformada de Laplace

La transformada de Fourier f̂ ( ξ ) está relacionada con la transformada de Laplace F ( s ) , que también se utiliza para la solución de ecuaciones diferenciales y el análisis de filtros .

Puede suceder que una función f para la cual la integral de Fourier no converge en absoluto al eje real, tenga sin embargo una transformada de Fourier compleja definida en alguna región del plano complejo .

Por ejemplo, si f ( t ) es de crecimiento exponencial, es decir, para algunas constantes C , a ≥ 0 , entonces ^[36] convergente para todo 2π τ < − a , es la transformada de Laplace de dos lados de f . $${\displaystyle \vert f(t)\vert <Ce^{a\vert t\vert }}$$ $${\displaystyle {\hat {f}}(i\tau )=\int _{-\infty }^{\infty }e^{2\pi \tau t}f(t)\,dt,}$$

La versión más habitual ("unilateral") de la transformada de Laplace es $${\displaystyle F(s)=\int _{0}^{\infty }f(t)e^{-st}\,dt.}$$

Si f también es causal y analítica, entonces: Por lo tanto, extender la transformada de Fourier al dominio complejo significa que incluye la transformada de Laplace como un caso especial en el caso de funciones causales, pero con el cambio de variable s = i 2π ξ . ${\displaystyle {\hat {f}}(i\tau )=F(-2\pi \tau ).}$

Desde otro punto de vista, quizás más clásico, la transformada de Laplace, por su forma, implica un término regulador exponencial adicional que le permite converger fuera de la línea imaginaria donde se define la transformada de Fourier. Como tal, puede converger para series e integrales exponencialmente divergentes como máximo, mientras que la descomposición de Fourier original no puede, lo que permite el análisis de sistemas con elementos divergentes o críticos. Dos ejemplos particulares del procesamiento de señales lineales son la construcción de redes de filtros pasatodo a partir de peines críticos y filtros de mitigación mediante la cancelación exacta de polos y ceros en el círculo unitario. Estos diseños son comunes en el procesamiento de audio, donde se busca una respuesta de fase altamente no lineal, como en la reverberación.

Además, cuando se buscan respuestas de impulsos extendidas de tipo pulso para el trabajo de procesamiento de señales, la forma más fácil de producirlas es tener un circuito que produzca una respuesta temporal divergente y luego cancelar su divergencia mediante una respuesta compensatoria opuesta y retardada. En este caso, solo el circuito de retardo intermedio admite una descripción clásica de Fourier, que es fundamental. Ambos circuitos laterales son inestables y no admiten una descomposición convergente de Fourier. Sin embargo, sí admiten una descripción del dominio de Laplace, con semiplanos de convergencia idénticos en el plano complejo (o en el caso discreto, el plano Z), en el que sus efectos se cancelan.

En las matemáticas modernas, la transformada de Laplace se engloba tradicionalmente en los métodos de Fourier, y ambos se engloban en la idea mucho más general y abstracta del análisis armónico .

Inversión

Aún con , si es analítica compleja para a ≤ τ ≤ b , entonces ${\displaystyle \xi =\sigma +i\tau }$ ${\displaystyle {\widehat {f}}}$

$${\displaystyle \int _{-\infty }^{\infty }{\hat {f}}(\sigma +ia)e^{i2\pi \xi t}\,d\sigma =\int _{-\infty }^{\infty }{\hat {f}}(\sigma +ib)e^{i2\pi \xi t}\,d\sigma }$$por el teorema integral de Cauchy . Por lo tanto, la fórmula de inversión de Fourier puede utilizar la integración a lo largo de diferentes líneas, paralelas al eje real. ^[37]

Teorema: Si f ( t ) = 0 para t < 0 , y | f ( t ) | < Ce ^{a | t |} para algunas constantes C , a > 0 , entonces para cualquier τ < − ⁠ $${\displaystyle f(t)=\int _{-\infty }^{\infty }{\hat {f}}(\sigma +i\tau )e^{i2\pi \xi t}\,d\sigma ,}$$a/2π⁠ .

Este teorema implica la fórmula de inversión de Mellin para la transformación de Laplace, ^[36] para cualquier b > a , donde F ( s ) es la transformada de Laplace de f ( t ) . $${\displaystyle f(t)={\frac {1}{i2\pi }}\int _{b-i\infty }^{b+i\infty }F(s)e^{st}\,ds}$$

Las hipótesis pueden debilitarse, como en los resultados de Carleson y Hunt, a f ( t ) e ^{− at} siendo L ¹ , siempre que f tenga una variación acotada en un entorno cerrado de t (cf. prueba de Dini ), que el valor de f en t se tome como la media aritmética de los límites izquierdo y derecho, y que las integrales se tomen en el sentido de los valores principales de Cauchy. ^[38]

También están disponibles versiones L2 de estas fórmulas ^{de inversión. [39]}

Transformada de Fourier en el espacio euclidiano

The Fourier transform can be defined in any arbitrary number of dimensions n. As with the one-dimensional case, there are many conventions. For an integrable function f(x), this article takes the definition: $${\displaystyle {\hat {f}}({\boldsymbol {\xi }})={\mathcal {F}}(f)({\boldsymbol {\xi }})=\int _{\mathbb {R} ^{n}}f(\mathbf {x} )e^{-i2\pi {\boldsymbol {\xi }}\cdot \mathbf {x} }\,d\mathbf {x} }$$where x and ξ are n-dimensional vectors, and x · ξ is the dot product of the vectors. Alternatively, ξ can be viewed as belonging to the dual vector space ${\displaystyle \mathbb {R} ^{n\star }}$, in which case the dot product becomes the contraction of x and ξ, usually written as ⟨x, ξ⟩.

All of the basic properties listed above hold for the n-dimensional Fourier transform, as do Plancherel's and Parseval's theorem. When the function is integrable, the Fourier transform is still uniformly continuous and the Riemann–Lebesgue lemma holds.^[11]

Uncertainty principle

Generally speaking, the more concentrated f(x) is, the more spread out its Fourier transform f̂(ξ) must be. In particular, the scaling property of the Fourier transform may be seen as saying: if we squeeze a function in x, its Fourier transform stretches out in ξ. It is not possible to arbitrarily concentrate both a function and its Fourier transform.

The trade-off between the compaction of a function and its Fourier transform can be formalized in the form of an uncertainty principle by viewing a function and its Fourier transform as conjugate variables with respect to the symplectic form on the time–frequency domain: from the point of view of the linear canonical transformation, the Fourier transform is rotation by 90° in the time–frequency domain, and preserves the symplectic form.

Suppose f(x) is an integrable and square-integrable function. Without loss of generality, assume that f(x) is normalized: $${\displaystyle \int _{-\infty }^{\infty }|f(x)|^{2}\,dx=1.}$$

It follows from the Plancherel theorem that f̂(ξ) is also normalized.

The spread around x = 0 may be measured by the dispersion about zero^[40] defined by $${\displaystyle D_{0}(f)=\int _{-\infty }^{\infty }x^{2}|f(x)|^{2}\,dx.}$$

In probability terms, this is the second moment of |f(x)|² about zero.

The uncertainty principle states that, if f(x) is absolutely continuous and the functions x·f(x) and f′(x) are square integrable, then^[14] $${\displaystyle D_{0}(f)D_{0}({\hat {f}})\geq {\frac {1}{16\pi ^{2}}}.}$$

The equality is attained only in the case $${\displaystyle {\begin{aligned}f(x)&=C_{1}\,e^{-\pi {\frac {x^{2}}{\sigma ^{2}}}}\\\therefore {\hat {f}}(\xi )&=\sigma C_{1}\,e^{-\pi \sigma ^{2}\xi ^{2}}\end{aligned}}}$$where σ > 0 is arbitrary and C₁ = ⁠⁴√2/√σ⁠ so that f is L²-normalized.^[14] In other words, where f is a (normalized) Gaussian function with variance σ²/2π, centered at zero, and its Fourier transform is a Gaussian function with variance σ⁻²/2π.

In fact, this inequality implies that: $${\displaystyle \left(\int _{-\infty }^{\infty }(x-x_{0})^{2}|f(x)|^{2}\,dx\right)\left(\int _{-\infty }^{\infty }(\xi -\xi _{0})^{2}\left|{\hat {f}}(\xi )\right|^{2}\,d\xi \right)\geq {\frac {1}{16\pi ^{2}}}}$$for any x₀, ξ₀ ∈ R.^[41]

In quantum mechanics, the momentum and position wave functions are Fourier transform pairs, up to a factor of the Planck constant. With this constant properly taken into account, the inequality above becomes the statement of the Heisenberg uncertainty principle.^[42]

A stronger uncertainty principle is the Hirschman uncertainty principle, which is expressed as: $${\displaystyle H\left(\left|f\right|^{2}\right)+H\left(\left|{\hat {f}}\right|^{2}\right)\geq \log \left({\frac {e}{2}}\right)}$$where H(p) is the differential entropy of the probability density function p(x): $${\displaystyle H(p)=-\int _{-\infty }^{\infty }p(x)\log {\bigl (}p(x){\bigr )}\,dx}$$where the logarithms may be in any base that is consistent. The equality is attained for a Gaussian, as in the previous case.

Sine and cosine transforms

Fourier's original formulation of the transform did not use complex numbers, but rather sines and cosines. Statisticians and others still use this form. An absolutely integrable function f for which Fourier inversion holds can be expanded in terms of genuine frequencies (avoiding negative frequencies, which are sometimes considered hard to interpret physically^[43]) λ by $${\displaystyle f(t)=\int _{0}^{\infty }{\bigl (}a(\lambda )\cos(2\pi \lambda t)+b(\lambda )\sin(2\pi \lambda t){\bigr )}\,d\lambda .}$$

This is called an expansion as a trigonometric integral, or a Fourier integral expansion. The coefficient functions a and b can be found by using variants of the Fourier cosine transform and the Fourier sine transform (the normalisations are, again, not standardised): $${\displaystyle a(\lambda )=2\int _{-\infty }^{\infty }f(t)\cos(2\pi \lambda t)\,dt}$$and $${\displaystyle b(\lambda )=2\int _{-\infty }^{\infty }f(t)\sin(2\pi \lambda t)\,dt.}$$

Older literature refers to the two transform functions, the Fourier cosine transform, a, and the Fourier sine transform, b.

The function f can be recovered from the sine and cosine transform using $${\displaystyle f(t)=2\int _{0}^{\infty }\int _{-\infty }^{\infty }f(\tau )\cos {\bigl (}2\pi \lambda (\tau -t){\bigr )}\,d\tau \,d\lambda .}$$together with trigonometric identities. This is referred to as Fourier's integral formula.^{[36][44][45][46]}

Spherical harmonics

Let the set of homogeneous harmonic polynomials of degree k on Rⁿ be denoted by A_k. The set A_k consists of the solid spherical harmonics of degree k. The solid spherical harmonics play a similar role in higher dimensions to the Hermite polynomials in dimension one. Specifically, if f(x) = e^−π|x|2P(x) for some P(x) in A_k, then f̂(ξ) = i^−k f(ξ). Let the set H_k be the closure in L²(Rⁿ) of linear combinations of functions of the form f(|x|)P(x) where P(x) is in A_k. The space L²(Rⁿ) is then a direct sum of the spaces H_k and the Fourier transform maps each space H_k to itself and is possible to characterize the action of the Fourier transform on each space H_k.^[11]

Let f(x) = f₀(|x|)P(x) (with P(x) in A_k), then $${\displaystyle {\hat {f}}(\xi )=F_{0}(|\xi |)P(\xi )}$$where $${\displaystyle F_{0}(r)=2\pi i^{-k}r^{-{\frac {n+2k-2}{2}}}\int _{0}^{\infty }f_{0}(s)J_{\frac {n+2k-2}{2}}(2\pi rs)s^{\frac {n+2k}{2}}\,ds.}$$

Here J_{(n + 2k − 2)/2} denotes the Bessel function of the first kind with order ⁠n + 2k − 2/2⁠. When k = 0 this gives a useful formula for the Fourier transform of a radial function.^[47] This is essentially the Hankel transform. Moreover, there is a simple recursion relating the cases n + 2 and n^[48] allowing to compute, e.g., the three-dimensional Fourier transform of a radial function from the one-dimensional one.

Restriction problems

In higher dimensions it becomes interesting to study restriction problems for the Fourier transform. The Fourier transform of an integrable function is continuous and the restriction of this function to any set is defined. But for a square-integrable function the Fourier transform could be a general class of square integrable functions. As such, the restriction of the Fourier transform of an L²(Rⁿ) function cannot be defined on sets of measure 0. It is still an active area of study to understand restriction problems in L^p for 1 < p < 2. It is possible in some cases to define the restriction of a Fourier transform to a set S, provided S has non-zero curvature. The case when S is the unit sphere in Rⁿ is of particular interest. In this case the Tomas–Stein restriction theorem states that the restriction of the Fourier transform to the unit sphere in Rⁿ is a bounded operator on L^p provided 1 ≤ p ≤ ⁠2n + 2/n + 3⁠.

One notable difference between the Fourier transform in 1 dimension versus higher dimensions concerns the partial sum operator. Consider an increasing collection of measurable sets E_R indexed by R ∈ (0,∞): such as balls of radius R centered at the origin, or cubes of side 2R. For a given integrable function f, consider the function f_R defined by: $${\displaystyle f_{R}(x)=\int _{E_{R}}{\hat {f}}(\xi )e^{i2\pi x\cdot \xi }\,d\xi ,\quad x\in \mathbb {R} ^{n}.}$$

Suppose in addition that f ∈ L^p(Rⁿ). For n = 1 and 1 < p < ∞, if one takes E_R = (−R, R), then f_R converges to f in L^p as R tends to infinity, by the boundedness of the Hilbert transform. Naively one may hope the same holds true for n > 1. In the case that E_R is taken to be a cube with side length R, then convergence still holds. Another natural candidate is the Euclidean ball E_R = {ξ : |ξ| < R}. In order for this partial sum operator to converge, it is necessary that the multiplier for the unit ball be bounded in L^p(Rⁿ). For n ≥ 2 it is a celebrated theorem of Charles Fefferman that the multiplier for the unit ball is never bounded unless p = 2.^[23] In fact, when p ≠ 2, this shows that not only may f_R fail to converge to f in L^p, but for some functions f ∈ L^p(Rⁿ), f_R is not even an element of L^p.

Fourier transform on function spaces

On Lp spaces

On L¹

The definition of the Fourier transform by the integral formula $${\displaystyle {\hat {f}}(\xi )=\int _{\mathbb {R} ^{n}}f(x)e^{-i2\pi \xi \cdot x}\,dx}$$is valid for Lebesgue integrable functions f; that is, f ∈ L¹(Rⁿ).

The Fourier transform F : L¹(Rⁿ) → L^∞(Rⁿ) is a bounded operator. This follows from the observation that $${\displaystyle \left\vert {\hat {f}}(\xi )\right\vert \leq \int _{\mathbb {R} ^{n}}\vert f(x)\vert \,dx,}$$which shows that its operator norm is bounded by 1. Indeed, it equals 1, which can be seen, for example, from the transform of the rect function. The image of L¹ is a subset of the space C₀(Rⁿ) of continuous functions that tend to zero at infinity (the Riemann–Lebesgue lemma), although it is not the entire space. Indeed, there is no simple characterization of the image.

On L²

Since compactly supported smooth functions are integrable and dense in L²(Rⁿ), the Plancherel theorem allows one to extend the definition of the Fourier transform to general functions in L²(Rⁿ) by continuity arguments. The Fourier transform in L²(Rⁿ) is no longer given by an ordinary Lebesgue integral, although it can be computed by an improper integral, here meaning that for an L² function f, $${\displaystyle {\hat {f}}(\xi )=\lim _{R\to \infty }\int _{|x|\leq R}f(x)e^{-i2\pi \xi \cdot x}\,dx}$$where the limit is taken in the L² sense.^[49][50])

Many of the properties of the Fourier transform in L¹ carry over to L², by a suitable limiting argument.

Furthermore, F : L²(Rⁿ) → L²(Rⁿ) is a unitary operator.^[51] For an operator to be unitary it is sufficient to show that it is bijective and preserves the inner product, so in this case these follow from the Fourier inversion theorem combined with the fact that for any f, g ∈ L²(Rⁿ) we have $${\displaystyle \int _{\mathbb {R} ^{n}}f(x){\mathcal {F}}g(x)\,dx=\int _{\mathbb {R} ^{n}}{\mathcal {F}}f(x)g(x)\,dx.}$$

In particular, the image of L²(Rⁿ) is itself under the Fourier transform.

On other L^p

The definition of the Fourier transform can be extended to functions in L^p(Rⁿ) for 1 ≤ p ≤ 2 by decomposing such functions into a fat tail part in L² plus a fat body part in L¹. In each of these spaces, the Fourier transform of a function in L^p(Rⁿ) is in L^q(Rⁿ), where q = ⁠p/p − 1⁠ is the Hölder conjugate of p (by the Hausdorff–Young inequality). However, except for p = 2, the image is not easily characterized. Further extensions become more technical. The Fourier transform of functions in L^p for the range 2 < p < ∞ requires the study of distributions.^[16] In fact, it can be shown that there are functions in L^p with p > 2 so that the Fourier transform is not defined as a function.^[11]

Tempered distributions

One might consider enlarging the domain of the Fourier transform from L¹ + L² by considering generalized functions, or distributions. A distribution on Rⁿ is a continuous linear functional on the space C_c(Rⁿ) of compactly supported smooth functions, equipped with a suitable topology. The strategy is then to consider the action of the Fourier transform on C_c(Rⁿ) and pass to distributions by duality. The obstruction to doing this is that the Fourier transform does not map C_c(Rⁿ) to C_c(Rⁿ). In fact the Fourier transform of an element in C_c(Rⁿ) can not vanish on an open set; see the above discussion on the uncertainty principle. The right space here is the slightly larger space of Schwartz functions. The Fourier transform is an automorphism on the Schwartz space, as a topological vector space, and thus induces an automorphism on its dual, the space of tempered distributions.^[11] The tempered distributions include all the integrable functions mentioned above, as well as well-behaved functions of polynomial growth and distributions of compact support.

For the definition of the Fourier transform of a tempered distribution, let f and g be integrable functions, and let f̂ and ĝ be their Fourier transforms respectively. Then the Fourier transform obeys the following multiplication formula,^[11] $${\displaystyle \int _{\mathbb {R} ^{n}}{\hat {f}}(x)g(x)\,dx=\int _{\mathbb {R} ^{n}}f(x){\hat {g}}(x)\,dx.}$$

Every integrable function f defines (induces) a distribution T_f by the relation $${\displaystyle T_{f}(\varphi )=\int _{\mathbb {R} ^{n}}f(x)\varphi (x)\,dx}$$for all Schwartz functions φ. So it makes sense to define Fourier transform T̂_f of T_f by $${\displaystyle {\hat {T}}_{f}(\varphi )=T_{f}\left({\hat {\varphi }}\right)}$$for all Schwartz functions φ. Extending this to all tempered distributions T gives the general definition of the Fourier transform.

Distributions can be differentiated and the above-mentioned compatibility of the Fourier transform with differentiation and convolution remains true for tempered distributions.

Generalizations

Fourier–Stieltjes transform

The Fourier transform of a finite Borel measure μ on Rⁿ is given by:^[52] $${\displaystyle {\hat {\mu }}(\xi )=\int _{\mathbb {R} ^{n}}e^{-i2\pi x\cdot \xi }\,d\mu .}$$

This transform continues to enjoy many of the properties of the Fourier transform of integrable functions. One notable difference is that the Riemann–Lebesgue lemma fails for measures.^[16] In the case that dμ = f(x) dx, then the formula above reduces to the usual definition for the Fourier transform of f. In the case that μ is the probability distribution associated to a random variable X, the Fourier–Stieltjes transform is closely related to the characteristic function, but the typical conventions in probability theory take e^iξx instead of e^−i2πξx.^[14] In the case when the distribution has a probability density function this definition reduces to the Fourier transform applied to the probability density function, again with a different choice of constants.

The Fourier transform may be used to give a characterization of measures. Bochner's theorem characterizes which functions may arise as the Fourier–Stieltjes transform of a positive measure on the circle.^[16]

Furthermore, the Dirac delta function, although not a function, is a finite Borel measure. Its Fourier transform is a constant function (whose specific value depends upon the form of the Fourier transform used).

Locally compact abelian groups

The Fourier transform may be generalized to any locally compact abelian group. A locally compact abelian group is an abelian group that is at the same time a locally compact Hausdorff topological space so that the group operation is continuous. If G is a locally compact abelian group, it has a translation invariant measure μ, called Haar measure. For a locally compact abelian group G, the set of irreducible, i.e. one-dimensional, unitary representations are called its characters. With its natural group structure and the topology of uniform convergence on compact sets (that is, the topology induced by the compact-open topology on the space of all continuous functions from ${\displaystyle G}$ to the circle group), the set of characters Ĝ is itself a locally compact abelian group, called the Pontryagin dual of G. For a function f in L¹(G), its Fourier transform is defined by^[16] $${\displaystyle {\hat {f}}(\xi )=\int _{G}\xi (x)f(x)\,d\mu \quad {\text{for any }}\xi \in {\hat {G}}.}$$

The Riemann–Lebesgue lemma holds in this case; f̂(ξ) is a function vanishing at infinity on Ĝ.

The Fourier transform on T = R/Z is an example; here T is a locally compact abelian group, and the Haar measure μ on T can be thought of as the Lebesgue measure on [0,1). Consider the representation of T on the complex plane C that is a 1-dimensional complex vector space. There are a group of representations (which are irreducible since C is 1-dim) ${\displaystyle \{e_{k}:T\rightarrow GL_{1}(C)=C^{*}\mid k\in Z\}}$ where ${\displaystyle e_{k}(x)=e^{i2\pi kx}}$ for ${\displaystyle x\in T}$.

The character of such representation, that is the trace of ${\displaystyle e_{k}(x)}$ for each ${\displaystyle x\in T}$ and ${\displaystyle k\in Z}$, is ${\displaystyle e^{i2\pi kx}}$ itself. In the case of representation of finite group, the character table of the group G are rows of vectors such that each row is the character of one irreducible representation of G, and these vectors form an orthonormal basis of the space of class functions that map from G to C by Schur's lemma. Now the group T is no longer finite but still compact, and it preserves the orthonormality of character table. Each row of the table is the function ${\displaystyle e_{k}(x)}$ of ${\displaystyle x\in T,}$ and the inner product between two class functions (all functions being class functions since T is abelian) ${\displaystyle f,g\in L^{2}(T,d\mu )}$ is defined as ${\textstyle \langle f,g\rangle ={\frac {1}{|T|}}\int _{[0,1)}f(y){\overline {g}}(y)d\mu (y)}$ with the normalizing factor ${\displaystyle |T|=1}$. The sequence ${\displaystyle \{e_{k}\mid k\in Z\}}$ is an orthonormal basis of the space of class functions ${\displaystyle L^{2}(T,d\mu )}$.

For any representation V of a finite group G, ${\displaystyle \chi _{v}}$ can be expressed as the span ${\textstyle \sum _{i}\left\langle \chi _{v},\chi _{v_{i}}\right\rangle \chi _{v_{i}}}$ ( ${\displaystyle V_{i}}$ are the irreps of G), such that ${\textstyle \left\langle \chi _{v},\chi _{v_{i}}\right\rangle ={\frac {1}{|G|}}\sum _{g\in G}\chi _{v}(g){\overline {\chi }}_{v_{i}}(g)}$. Similarly for ${\displaystyle G=T}$ and ${\displaystyle f\in L^{2}(T,d\mu )}$, ${\textstyle f(x)=\sum _{k\in Z}{\hat {f}}(k)e_{k}}$. The Pontriagin dual ${\displaystyle {\hat {T}}}$ is ${\displaystyle \{e_{k}\}(k\in Z)}$ and for ${\displaystyle f\in L^{2}(T,d\mu )}$, ${\textstyle {\hat {f}}(k)={\frac {1}{|T|}}\int _{[0,1)}f(y)e^{-i2\pi ky}dy}$ is its Fourier transform for ${\displaystyle e_{k}\in {\hat {T}}}$.

Gelfand transform

The Fourier transform is also a special case of Gelfand transform. In this particular context, it is closely related to the Pontryagin duality map defined above.

Given an abelian locally compact Hausdorff topological group G, as before we consider space L¹(G), defined using a Haar measure. With convolution as multiplication, L¹(G) is an abelian Banach algebra. It also has an involution * given by $${\displaystyle f^{*}(g)={\overline {f\left(g^{-1}\right)}}.}$$

Taking the completion with respect to the largest possibly C*-norm gives its enveloping C*-algebra, called the group C*-algebra C*(G) of G. (Any C*-norm on L¹(G) is bounded by the L¹ norm, therefore their supremum exists.)

Given any abelian C*-algebra A, the Gelfand transform gives an isomorphism between A and C₀(A^), where A^ is the multiplicative linear functionals, i.e. one-dimensional representations, on A with the weak-* topology. The map is simply given by $${\displaystyle a\mapsto {\bigl (}\varphi \mapsto \varphi (a){\bigr )}}$$It turns out that the multiplicative linear functionals of C*(G), after suitable identification, are exactly the characters of G, and the Gelfand transform, when restricted to the dense subset L¹(G) is the Fourier–Pontryagin transform.

Compact non-abelian groups

The Fourier transform can also be defined for functions on a non-abelian group, provided that the group is compact. Removing the assumption that the underlying group is abelian, irreducible unitary representations need not always be one-dimensional. This means the Fourier transform on a non-abelian group takes values as Hilbert space operators.^[53] The Fourier transform on compact groups is a major tool in representation theory^[54] and non-commutative harmonic analysis.

Let G be a compact Hausdorff topological group. Let Σ denote the collection of all isomorphism classes of finite-dimensional irreducible unitary representations, along with a definite choice of representation U^(σ) on the Hilbert space H_σ of finite dimension d_σ for each σ ∈ Σ. If μ is a finite Borel measure on G, then the Fourier–Stieltjes transform of μ is the operator on H_σ defined by $${\displaystyle \left\langle {\hat {\mu }}\xi ,\eta \right\rangle _{H_{\sigma }}=\int _{G}\left\langle {\overline {U}}_{g}^{(\sigma )}\xi ,\eta \right\rangle \,d\mu (g)}$$where U^(σ) is the complex-conjugate representation of U^(σ) acting on H_σ. If μ is absolutely continuous with respect to the left-invariant probability measure λ on G, represented as $${\displaystyle d\mu =f\,d\lambda }$$for some f ∈ L¹(λ), one identifies the Fourier transform of f with the Fourier–Stieltjes transform of μ.

The mapping $${\displaystyle \mu \mapsto {\hat {\mu }}}$$defines an isomorphism between the Banach space M(G) of finite Borel measures (see rca space) and a closed subspace of the Banach space C_∞(Σ) consisting of all sequences E = (E_σ) indexed by Σ of (bounded) linear operators E_σ : H_σ → H_σ for which the norm $${\displaystyle \|E\|=\sup _{\sigma \in \Sigma }\left\|E_{\sigma }\right\|}$$is finite. The "convolution theorem" asserts that, furthermore, this isomorphism of Banach spaces is in fact an isometric isomorphism of C*-algebras into a subspace of C_∞(Σ). Multiplication on M(G) is given by convolution of measures and the involution * defined by $${\displaystyle f^{*}(g)={\overline {f\left(g^{-1}\right)}},}$$and C_∞(Σ) has a natural C*-algebra structure as Hilbert space operators.

The Peter–Weyl theorem holds, and a version of the Fourier inversion formula (Plancherel's theorem) follows: if f ∈ L²(G), then $${\displaystyle f(g)=\sum _{\sigma \in \Sigma }d_{\sigma }\operatorname {tr} \left({\hat {f}}(\sigma )U_{g}^{(\sigma )}\right)}$$where the summation is understood as convergent in the L² sense.

The generalization of the Fourier transform to the noncommutative situation has also in part contributed to the development of noncommutative geometry.^{[citation needed]} In this context, a categorical generalization of the Fourier transform to noncommutative groups is Tannaka–Krein duality, which replaces the group of characters with the category of representations. However, this loses the connection with harmonic functions.

Alternatives

In signal processing terms, a function (of time) is a representation of a signal with perfect time resolution, but no frequency information, while the Fourier transform has perfect frequency resolution, but no time information: the magnitude of the Fourier transform at a point is how much frequency content there is, but location is only given by phase (argument of the Fourier transform at a point), and standing waves are not localized in time – a sine wave continues out to infinity, without decaying. This limits the usefulness of the Fourier transform for analyzing signals that are localized in time, notably transients, or any signal of finite extent.

As alternatives to the Fourier transform, in time–frequency analysis, one uses time–frequency transforms or time–frequency distributions to represent signals in a form that has some time information and some frequency information – by the uncertainty principle, there is a trade-off between these. These can be generalizations of the Fourier transform, such as the short-time Fourier transform, fractional Fourier transform, Synchrosqueezing Fourier transform,^[55] or other functions to represent signals, as in wavelet transforms and chirplet transforms, with the wavelet analog of the (continuous) Fourier transform being the continuous wavelet transform.^[24]

Applications

Some problems, such as certain differential equations, become easier to solve when the Fourier transform is applied. In that case the solution to the original problem is recovered using the inverse Fourier transform.

Linear operations performed in one domain (time or frequency) have corresponding operations in the other domain, which are sometimes easier to perform. The operation of differentiation in the time domain corresponds to multiplication by the frequency,^{[note 6]} so some differential equations are easier to analyze in the frequency domain. Also, convolution in the time domain corresponds to ordinary multiplication in the frequency domain (see Convolution theorem). After performing the desired operations, transformation of the result can be made back to the time domain. Harmonic analysis is the systematic study of the relationship between the frequency and time domains, including the kinds of functions or operations that are "simpler" in one or the other, and has deep connections to many areas of modern mathematics.

Analysis of differential equations

Perhaps the most important use of the Fourier transformation is to solve partial differential equations. Many of the equations of the mathematical physics of the nineteenth century can be treated this way. Fourier studied the heat equation, which in one dimension and in dimensionless units is $${\displaystyle {\frac {\partial ^{2}y(x,t)}{\partial ^{2}x}}={\frac {\partial y(x,t)}{\partial t}}.}$$The example we will give, a slightly more difficult one, is the wave equation in one dimension, $${\displaystyle {\frac {\partial ^{2}y(x,t)}{\partial ^{2}x}}={\frac {\partial ^{2}y(x,t)}{\partial ^{2}t}}.}$$

As usual, the problem is not to find a solution: there are infinitely many. The problem is that of the so-called "boundary problem": find a solution which satisfies the "boundary conditions" $${\displaystyle y(x,0)=f(x),\qquad {\frac {\partial y(x,0)}{\partial t}}=g(x).}$$

Here, f and g are given functions. For the heat equation, only one boundary condition can be required (usually the first one). But for the wave equation, there are still infinitely many solutions y which satisfy the first boundary condition. But when one imposes both conditions, there is only one possible solution.

It is easier to find the Fourier transform ŷ of the solution than to find the solution directly. This is because the Fourier transformation takes differentiation into multiplication by the Fourier-dual variable, and so a partial differential equation applied to the original function is transformed into multiplication by polynomial functions of the dual variables applied to the transformed function. After ŷ is determined, we can apply the inverse Fourier transformation to find y.

Fourier's method is as follows. First, note that any function of the forms $${\displaystyle \cos {\bigl (}2\pi \xi (x\pm t){\bigr )}{\text{ or }}\sin {\bigl (}2\pi \xi (x\pm t){\bigr )}}$$satisfies the wave equation. These are called the elementary solutions.

Second, note that therefore any integral $${\displaystyle {\begin{aligned}y(x,t)=\int _{0}^{\infty }d\xi {\Bigl [}&a_{+}(\xi )\cos {\bigl (}2\pi \xi (x+t){\bigr )}+a_{-}(\xi )\cos {\bigl (}2\pi \xi (x-t){\bigr )}+{}\\&b_{+}(\xi )\sin {\bigl (}2\pi \xi (x+t){\bigr )}+b_{-}(\xi )\sin \left(2\pi \xi (x-t)\right){\Bigr ]}\end{aligned}}}$$satisfies the wave equation for arbitrary a₊, a₋, b₊, b₋. This integral may be interpreted as a continuous linear combination of solutions for the linear equation.

Now this resembles the formula for the Fourier synthesis of a function. In fact, this is the real inverse Fourier transform of a_± and b_± in the variable x.

The third step is to examine how to find the specific unknown coefficient functions a_± and b_± that will lead to y satisfying the boundary conditions. We are interested in the values of these solutions at t = 0. So we will set t = 0. Assuming that the conditions needed for Fourier inversion are satisfied, we can then find the Fourier sine and cosine transforms (in the variable x) of both sides and obtain $${\displaystyle 2\int _{-\infty }^{\infty }y(x,0)\cos(2\pi \xi x)\,dx=a_{+}+a_{-}}$$and $${\displaystyle 2\int _{-\infty }^{\infty }y(x,0)\sin(2\pi \xi x)\,dx=b_{+}+b_{-}.}$$

Similarly, taking the derivative of y with respect to t and then applying the Fourier sine and cosine transformations yields $${\displaystyle 2\int _{-\infty }^{\infty }{\frac {\partial y(u,0)}{\partial t}}\sin(2\pi \xi x)\,dx=(2\pi \xi )\left(-a_{+}+a_{-}\right)}$$and $${\displaystyle 2\int _{-\infty }^{\infty }{\frac {\partial y(u,0)}{\partial t}}\cos(2\pi \xi x)\,dx=(2\pi \xi )\left(b_{+}-b_{-}\right).}$$

These are four linear equations for the four unknowns a_± and b_±, in terms of the Fourier sine and cosine transforms of the boundary conditions, which are easily solved by elementary algebra, provided that these transforms can be found.

In summary, we chose a set of elementary solutions, parametrized by ξ, of which the general solution would be a (continuous) linear combination in the form of an integral over the parameter ξ. But this integral was in the form of a Fourier integral. The next step was to express the boundary conditions in terms of these integrals, and set them equal to the given functions f and g. But these expressions also took the form of a Fourier integral because of the properties of the Fourier transform of a derivative. The last step was to exploit Fourier inversion by applying the Fourier transformation to both sides, thus obtaining expressions for the coefficient functions a_± and b_± in terms of the given boundary conditions f and g.

From a higher point of view, Fourier's procedure can be reformulated more conceptually. Since there are two variables, we will use the Fourier transformation in both x and t rather than operate as Fourier did, who only transformed in the spatial variables. Note that ŷ must be considered in the sense of a distribution since y(x, t) is not going to be L¹: as a wave, it will persist through time and thus is not a transient phenomenon. But it will be bounded and so its Fourier transform can be defined as a distribution. The operational properties of the Fourier transformation that are relevant to this equation are that it takes differentiation in x to multiplication by i2πξ and differentiation with respect to t to multiplication by i2πf where f is the frequency. Then the wave equation becomes an algebraic equation in ŷ: $${\displaystyle \xi ^{2}{\hat {y}}(\xi ,f)=f^{2}{\hat {y}}(\xi ,f).}$$This is equivalent to requiring ŷ(ξ, f) = 0 unless ξ = ±f. Right away, this explains why the choice of elementary solutions we made earlier worked so well: obviously f̂ = δ(ξ ± f) will be solutions. Applying Fourier inversion to these delta functions, we obtain the elementary solutions we picked earlier. But from the higher point of view, one does not pick elementary solutions, but rather considers the space of all distributions which are supported on the (degenerate) conic ξ² − f² = 0.

We may as well consider the distributions supported on the conic that are given by distributions of one variable on the line ξ = f plus distributions on the line ξ = −f as follows: if Φ is any test function, $${\displaystyle \iint {\hat {y}}\phi (\xi ,f)\,d\xi \,df=\int s_{+}\phi (\xi ,\xi )\,d\xi +\int s_{-}\phi (\xi ,-\xi )\,d\xi ,}$$where s₊, and s₋, are distributions of one variable.

Then Fourier inversion gives, for the boundary conditions, something very similar to what we had more concretely above (put Φ(ξ, f) = e^i2π(xξ+tf), which is clearly of polynomial growth): $${\displaystyle y(x,0)=\int {\bigl \{}s_{+}(\xi )+s_{-}(\xi ){\bigr \}}e^{i2\pi \xi x+0}\,d\xi }$$and $${\displaystyle {\frac {\partial y(x,0)}{\partial t}}=\int {\bigl \{}s_{+}(\xi )-s_{-}(\xi ){\bigr \}}i2\pi \xi e^{i2\pi \xi x+0}\,d\xi .}$$

Now, as before, applying the one-variable Fourier transformation in the variable x to these functions of x yields two equations in the two unknown distributions s_± (which can be taken to be ordinary functions if the boundary conditions are L¹ or L²).

From a calculational point of view, the drawback of course is that one must first calculate the Fourier transforms of the boundary conditions, then assemble the solution from these, and then calculate an inverse Fourier transform. Closed form formulas are rare, except when there is some geometric symmetry that can be exploited, and the numerical calculations are difficult because of the oscillatory nature of the integrals, which makes convergence slow and hard to estimate. For practical calculations, other methods are often used.

The twentieth century has seen the extension of these methods to all linear partial differential equations with polynomial coefficients, and by extending the notion of Fourier transformation to include Fourier integral operators, some non-linear equations as well.

Fourier-transform spectroscopy

The Fourier transform is also used in nuclear magnetic resonance (NMR) and in other kinds of spectroscopy, e.g. infrared (FTIR). In NMR an exponentially shaped free induction decay (FID) signal is acquired in the time domain and Fourier-transformed to a Lorentzian line-shape in the frequency domain. The Fourier transform is also used in magnetic resonance imaging (MRI) and mass spectrometry.

Quantum mechanics

The Fourier transform is useful in quantum mechanics in at least two different ways. To begin with, the basic conceptual structure of quantum mechanics postulates the existence of pairs of complementary variables, connected by the Heisenberg uncertainty principle. For example, in one dimension, the spatial variable q of, say, a particle, can only be measured by the quantum mechanical "position operator" at the cost of losing information about the momentum p of the particle. Therefore, the physical state of the particle can either be described by a function, called "the wave function", of q or by a function of p but not by a function of both variables. The variable p is called the conjugate variable to q. In classical mechanics, the physical state of a particle (existing in one dimension, for simplicity of exposition) would be given by assigning definite values to both p and q simultaneously. Thus, the set of all possible physical states is the two-dimensional real vector space with a p-axis and a q-axis called the phase space.

In contrast, quantum mechanics chooses a polarisation of this space in the sense that it picks a subspace of one-half the dimension, for example, the q-axis alone, but instead of considering only points, takes the set of all complex-valued "wave functions" on this axis. Nevertheless, choosing the p-axis is an equally valid polarisation, yielding a different representation of the set of possible physical states of the particle. Both representations of the wavefunction are related by a Fourier transform, such that $${\displaystyle \phi (p)=\int dq\,\psi (q)e^{-ipq/h},}$$or, equivalently, $${\displaystyle \psi (q)=\int dp\,\phi (p)e^{ipq/h}.}$$

Physically realisable states are L², and so by the Plancherel theorem, their Fourier transforms are also L². (Note that since q is in units of distance and p is in units of momentum, the presence of the Planck constant in the exponent makes the exponent dimensionless, as it should be.)

Therefore, the Fourier transform can be used to pass from one way of representing the state of the particle, by a wave function of position, to another way of representing the state of the particle: by a wave function of momentum. Infinitely many different polarisations are possible, and all are equally valid. Being able to transform states from one representation to another by the Fourier transform is not only convenient but also the underlying reason of the Heisenberg uncertainty principle.

The other use of the Fourier transform in both quantum mechanics and quantum field theory is to solve the applicable wave equation. In non-relativistic quantum mechanics, Schrödinger's equation for a time-varying wave function in one-dimension, not subject to external forces, is $${\displaystyle -{\frac {\partial ^{2}}{\partial x^{2}}}\psi (x,t)=i{\frac {h}{2\pi }}{\frac {\partial }{\partial t}}\psi (x,t).}$$

This is the same as the heat equation except for the presence of the imaginary unit i. Fourier methods can be used to solve this equation.

In the presence of a potential, given by the potential energy function V(x), the equation becomes $${\displaystyle -{\frac {\partial ^{2}}{\partial x^{2}}}\psi (x,t)+V(x)\psi (x,t)=i{\frac {h}{2\pi }}{\frac {\partial }{\partial t}}\psi (x,t).}$$

The "elementary solutions", as we referred to them above, are the so-called "stationary states" of the particle, and Fourier's algorithm, as described above, can still be used to solve the boundary value problem of the future evolution of ψ given its values for t = 0. Neither of these approaches is of much practical use in quantum mechanics. Boundary value problems and the time-evolution of the wave function is not of much practical interest: it is the stationary states that are most important.

In relativistic quantum mechanics, Schrödinger's equation becomes a wave equation as was usual in classical physics, except that complex-valued waves are considered. A simple example, in the absence of interactions with other particles or fields, is the free one-dimensional Klein–Gordon–Schrödinger–Fock equation, this time in dimensionless units, $${\displaystyle \left({\frac {\partial ^{2}}{\partial x^{2}}}+1\right)\psi (x,t)={\frac {\partial ^{2}}{\partial t^{2}}}\psi (x,t).}$$

This is, from the mathematical point of view, the same as the wave equation of classical physics solved above (but with a complex-valued wave, which makes no difference in the methods). This is of great use in quantum field theory: each separate Fourier component of a wave can be treated as a separate harmonic oscillator and then quantized, a procedure known as "second quantization". Fourier methods have been adapted to also deal with non-trivial interactions.

Finally, the number operator of the quantum harmonic oscillator can be interpreted, for example via the Mehler kernel, as the generator of the Fourier transform ${\displaystyle {\mathcal {F}}}$.^[27]

Signal processing

The Fourier transform is used for the spectral analysis of time-series. The subject of statistical signal processing does not, however, usually apply the Fourier transformation to the signal itself. Even if a real signal is indeed transient, it has been found in practice advisable to model a signal by a function (or, alternatively, a stochastic process) which is stationary in the sense that its characteristic properties are constant over all time. The Fourier transform of such a function does not exist in the usual sense, and it has been found more useful for the analysis of signals to instead take the Fourier transform of its autocorrelation function.

The autocorrelation function R of a function f is defined by $${\displaystyle R_{f}(\tau )=\lim _{T\rightarrow \infty }{\frac {1}{2T}}\int _{-T}^{T}f(t)f(t+\tau )\,dt.}$$

This function is a function of the time-lag τ elapsing between the values of f to be correlated.

For most functions f that occur in practice, R is a bounded even function of the time-lag τ and for typical noisy signals it turns out to be uniformly continuous with a maximum at τ = 0.

The autocorrelation function, more properly called the autocovariance function unless it is normalized in some appropriate fashion, measures the strength of the correlation between the values of f separated by a time lag. This is a way of searching for the correlation of f with its own past. It is useful even for other statistical tasks besides the analysis of signals. For example, if f(t) represents the temperature at time t, one expects a strong correlation with the temperature at a time lag of 24 hours.

It possesses a Fourier transform, $${\displaystyle P_{f}(\xi )=\int _{-\infty }^{\infty }R_{f}(\tau )e^{-i2\pi \xi \tau }\,d\tau .}$$

This Fourier transform is called the power spectral density function of f. (Unless all periodic components are first filtered out from f, this integral will diverge, but it is easy to filter out such periodicities.)

The power spectrum, as indicated by this density function P, measures the amount of variance contributed to the data by the frequency ξ. In electrical signals, the variance is proportional to the average power (energy per unit time), and so the power spectrum describes how much the different frequencies contribute to the average power of the signal. This process is called the spectral analysis of time-series and is analogous to the usual analysis of variance of data that is not a time-series (ANOVA).

Knowledge of which frequencies are "important" in this sense is crucial for the proper design of filters and for the proper evaluation of measuring apparatuses. It can also be useful for the scientific analysis of the phenomena responsible for producing the data.

The power spectrum of a signal can also be approximately measured directly by measuring the average power that remains in a signal after all the frequencies outside a narrow band have been filtered out.

Spectral analysis is carried out for visual signals as well. The power spectrum ignores all phase relations, which is good enough for many purposes, but for video signals other types of spectral analysis must also be employed, still using the Fourier transform as a tool.

Other notations

Other common notations for ${\displaystyle {\hat {f}}(\xi )}$ include: $${\displaystyle {\tilde {f}}(\xi ),\ F(\xi ),\ {\mathcal {F}}\left(f\right)(\xi ),\ \left({\mathcal {F}}f\right)(\xi ),\ {\mathcal {F}}(f),\ {\mathcal {F}}\{f\},\ {\mathcal {F}}{\bigl (}f(t){\bigr )},\ {\mathcal {F}}{\bigl \{}f(t){\bigr \}}.}$$

In the sciences and engineering it is also common to make substitutions like these: $${\displaystyle \xi \rightarrow f,\quad x\rightarrow t,\quad f\rightarrow x,\quad {\hat {f}}\rightarrow X.}$$

So the transform pair ${\displaystyle f(x)\ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ {\hat {f}}(\xi )}$ can become ${\displaystyle x(t)\ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ X(f)}$

A disadvantage of the capital letter notation is when expressing a transform such as ${\displaystyle {\widehat {f\cdot g}}}$ or ${\displaystyle {\widehat {f'}},}$ which become the more awkward ${\displaystyle {\mathcal {F}}\{f\cdot g\}}$ and ${\displaystyle {\mathcal {F}}\{f'\}.}$

In some contexts such as particle physics, the same symbol ${\displaystyle f}$ may be used for both for a function as well as it Fourier transform, with the two only distinguished by their argument I.e. ${\displaystyle f(k_{1}+k_{2})}$ would refer to the Fourier transform because of the momentum argument, while ${\displaystyle f(x_{0}+\pi {\vec {r}})}$ would refer to the original function because of the positional argument. Although tildes may be used as in ${\displaystyle {\tilde {f}}}$ to indicate Fourier transforms, tildes may also be used to indicate a modification of a quantity with a more Lorentz invariant form, such as ${\displaystyle {\tilde {dk}}={\frac {dk}{(2\pi )^{3}2\omega }}}$, so care must be taken. Similarly, ${\displaystyle {\hat {f}}}$ often denotes the Hilbert transform of ${\displaystyle f}$.

The interpretation of the complex function f̂(ξ) may be aided by expressing it in polar coordinate form $${\displaystyle {\hat {f}}(\xi )=A(\xi )e^{i\varphi (\xi )}}$$in terms of the two real functions A(ξ) and φ(ξ) where: $${\displaystyle A(\xi )=\left|{\hat {f}}(\xi )\right|,}$$is the amplitude and $${\displaystyle \varphi (\xi )=\arg \left({\hat {f}}(\xi )\right),}$$is the phase (see arg function).

Then the inverse transform can be written: $${\displaystyle f(x)=\int _{-\infty }^{\infty }A(\xi )\ e^{i{\bigl (}2\pi \xi x+\varphi (\xi ){\bigr )}}\,d\xi ,}$$which is a recombination of all the frequency components of f(x). Each component is a complex sinusoid of the form e^2πixξ whose amplitude is A(ξ) and whose initial phase angle (at x = 0) is φ(ξ).

The Fourier transform may be thought of as a mapping on function spaces. This mapping is here denoted F and F(f) is used to denote the Fourier transform of the function f. This mapping is linear, which means that F can also be seen as a linear transformation on the function space and implies that the standard notation in linear algebra of applying a linear transformation to a vector (here the function f) can be used to write F f instead of F(f). Since the result of applying the Fourier transform is again a function, we can be interested in the value of this function evaluated at the value ξ for its variable, and this is denoted either as F f(ξ) or as (F f)(ξ). Notice that in the former case, it is implicitly understood that F is applied first to f and then the resulting function is evaluated at ξ, not the other way around.

In mathematics and various applied sciences, it is often necessary to distinguish between a function f and the value of f when its variable equals x, denoted f(x). This means that a notation like F(f(x)) formally can be interpreted as the Fourier transform of the values of f at x. Despite this flaw, the previous notation appears frequently, often when a particular function or a function of a particular variable is to be transformed. For example, $${\displaystyle {\mathcal {F}}{\bigl (}\operatorname {rect} (x){\bigr )}=\operatorname {sinc} (\xi )}$$is sometimes used to express that the Fourier transform of a rectangular function is a sinc function, or $${\displaystyle {\mathcal {F}}{\bigl (}f(x+x_{0}){\bigr )}={\mathcal {F}}{\bigl (}f(x){\bigr )}\,e^{i2\pi x_{0}\xi }}$$is used to express the shift property of the Fourier transform.

Notice, that the last example is only correct under the assumption that the transformed function is a function of x, not of x₀.

As discussed above, the characteristic function of a random variable is the same as the Fourier–Stieltjes transform of its distribution measure, but in this context it is typical to take a different convention for the constants. Typically characteristic function is defined $${\displaystyle E\left(e^{it\cdot X}\right)=\int e^{it\cdot x}\,d\mu _{X}(x).}$$

As in the case of the "non-unitary angular frequency" convention above, the factor of 2π appears in neither the normalizing constant nor the exponent. Unlike any of the conventions appearing above, this convention takes the opposite sign in the exponent.

Computation methods

The appropriate computation method largely depends how the original mathematical function is represented and the desired form of the output function. In this section we consider both functions of a continuous variable, ${\displaystyle f(x),}$ and functions of a discrete variable (i.e. ordered pairs of ${\displaystyle x}$ and ${\displaystyle f}$ values). For discrete-valued ${\displaystyle x,}$ the transform integral becomes a summation of sinusoids, which is still a continuous function of frequency ( ${\displaystyle \xi }$ or ${\displaystyle \omega }$). When the sinusoids are harmonically-related (i.e. when the ${\displaystyle x}$-values are spaced at integer multiples of an interval), the transform is called discrete-time Fourier transform (DTFT).

Discrete Fourier transforms and fast Fourier transforms

Sampling the DTFT at equally-spaced values of frequency is the most common modern method of computation. Efficient procedures, depending on the frequency resolution needed, are described at Discrete-time Fourier transform § Sampling the DTFT. The discrete Fourier transform (DFT), used there, is usually computed by a fast Fourier transform (FFT) algorithm.

Analytic integration of closed-form functions

Tables of closed-form Fourier transforms, such as § Square-integrable functions, one-dimensional and § Table of discrete-time Fourier transforms, are created by mathematically evaluating the Fourier analysis integral (or summation) into another closed-form function of frequency ( ${\displaystyle \xi }$ or ${\displaystyle \omega }$).^[56] When mathematically possible, this provides a transform for a continuum of frequency values.

Many computer algebra systems such as Matlab and Mathematica that are capable of symbolic integration are capable of computing Fourier transforms analytically. For example, to compute the Fourier transform of cos(6πt) e^−πt2 one might enter the command integrate cos(6*pi*t) exp(−pi*t^2) exp(-i*2*pi*f*t) from -inf to inf into Wolfram Alpha.^{[note 7]}

Numerical integration of closed-form continuous functions

Discrete sampling of the Fourier transform can also be done by numerical integration of the definition at each value of frequency for which transform is desired.^[57][58][59] The numerical integration approach works on a much broader class of functions than the analytic approach.

Numerical integration of a series of ordered pairs

If the input function is a series of ordered pairs, numerical integration reduces to just a summation over the set of data pairs.^[60] The DTFT is a common subcase of this more general situation.

Tables of important Fourier transforms

The following tables record some closed-form Fourier transforms. For functions f(x) and g(x) denote their Fourier transforms by f̂ and ĝ. Only the three most common conventions are included. It may be useful to notice that entry 105 gives a relationship between the Fourier transform of a function and the original function, which can be seen as relating the Fourier transform and its inverse.

Functional relationships, one-dimensional

The Fourier transforms in this table may be found in Erdélyi (1954) or Kammler (2000, appendix).

Square-integrable functions, one-dimensional

The Fourier transforms in this table may be found in Campbell & Foster (1948), Erdélyi (1954), or Kammler (2000, appendix).

Distributions, one-dimensional

The Fourier transforms in this table may be found in Erdélyi (1954) or Kammler (2000, appendix).

Two-dimensional functions

Formulas for general n-dimensional functions

See also

• Analog signal processing
• Beevers–Lipson strip
• Constant-Q transform
• Discrete Fourier transform
• *DFT matrix
• Fast Fourier transform
• Fourier integral operator
• Fourier inversion theorem
• Fourier multiplier
• Fourier series
• Fourier sine transform
• Fourier–Deligne transform
• Fourier–Mukai transform
• Fractional Fourier transform
• Indirect Fourier transform
• Integral transform
  • Hankel transform
  • Hartley transform
• Laplace transform
• Least-squares spectral analysis
• Linear canonical transform
• List of Fourier-related transforms
• Mellin transform
• Multidimensional transform
• NGC 4622, especially the image NGC 4622 Fourier transform m = 2.
• Nonlocal operator
• Quantum Fourier transform
• Quadratic Fourier transform
• Short-time Fourier transform
• Spectral density
  • Spectral density estimation
• Symbolic integration
• Time stretch dispersive Fourier transform
• Transform (mathematics)

Notes

1. Depending on the application a Lebesgue integral, distributional, or other approach may be most appropriate.
2. Vretblad (2000) provides solid justification for these formal procedures without going too deeply into functional analysis or the theory of distributions.
3. In relativistic quantum mechanics one encounters vector-valued Fourier transforms of multi-component wave functions. In quantum field theory, operator-valued Fourier transforms of operator-valued functions of spacetime are in frequent use, see for example Greiner & Reinhardt (1996).
4. A possible source of confusion is the frequency-shifting property; i.e. the transform of function ${\displaystyle f(x)e^{-i2\pi \xi _{0}x}}$ is ${\displaystyle {\widehat {f}}(\xi +\xi _{0}).}$  The value of this function at   ${\displaystyle \xi =0}$  is ${\displaystyle {\widehat {f}}(\xi _{0}),}$ meaning that a frequency ${\displaystyle \xi _{0}}$ has been shifted to zero (also see Negative frequency).
5. The operator ${\displaystyle U\left({\frac {1}{2\pi }}{\frac {d}{dx}}\right)}$ is defined by replacing ${\displaystyle x}$ by ${\displaystyle {\frac {1}{2\pi }}{\frac {d}{dx}}}$ in the Taylor expansion of ${\displaystyle U(x).}$
6. Up to an imaginary constant factor whose magnitude depends on what Fourier transform convention is used.
7. The direct command fourier transform of cos(6*pi*t) exp(−pi*t^2) would also work for Wolfram Alpha, although the options for the convention (see Fourier transform § Other conventions) must be changed away from the default option, which is actually equivalent to integrate cos(6*pi*t) exp(−pi*t^2) exp(i*omega*t) /sqrt(2*pi) from -inf to inf.
8. In Gelfand & Shilov 1964, p. 363, with the non-unitary conventions of this table, the transform of ${\displaystyle |\mathbf {x} |^{\lambda }}$ is given to be
   ${\displaystyle 2^{\lambda +n}\pi ^{{\tfrac {1}{2}}n}{\frac {\Gamma \left({\frac {\lambda +n}{2}}\right)}{\Gamma \left(-{\frac {\lambda }{2}}\right)}}|{\boldsymbol {\omega }}|^{-\lambda -n}}$
   from which this follows, with ${\displaystyle \lambda =-\alpha }$.

Citations

1. Khare, Butola & Rajora 2023, pp. 13–14
2. Kaiser 1994, p. 29
3. Rahman 2011, p. 11
4. Dym & McKean 1985
5. Fourier 1822, p. 525
6. Fourier 1878, p. 408
7. Jordan (1883) proves on pp. 216–226 the Fourier integral theorem before studying Fourier series.
8. Titchmarsh 1986, p. 1
9. Rahman 2011, p. 10.
10. Oppenheim, Schafer & Buck 1999, p. 58
11. Stein & Weiss 1971
12. Folland 1989
13. Fourier 1822
14. Pinsky 2002
15. Arfken 1985
16. Katznelson 1976
17. Rudin 1987, p. 187
18. Rudin 1987, p. 186
19. Folland 1992, p. 216
20. Wolf 1979, p. 307ff
21. Folland 1989, p. 53
22. Celeghini, Gadella & del Olmo 2021
23. Duoandikoetxea 2001
24. Boashash 2003
25. Condon 1937
26. Wolf 1979, p. 320
27. Wolf 1979, p. 312
28. Folland 1989, p. 52
29. Howe 1980
30. Paley & Wiener 1934
31. Gelfand & Vilenkin 1964
32. Kirillov & Gvishiani 1982
33. Clozel & Delorme 1985, pp. 331–333
34. de Groot & Mazur 1984, p. 146
35. Champeney 1987, p. 80
36. Kolmogorov & Fomin 1999
37. Wiener 1949
38. Champeney 1987, p. 63
39. Widder & Wiener 1938, p. 537
40. Pinsky 2002, p. 131
41. Stein & Shakarchi 2003
42. Stein & Shakarchi 2003, p. 158
43. Chatfield 2004, p. 113
44. Fourier 1822, p. 441
45. Poincaré 1895, p. 102
46. Whittaker & Watson 1927, p. 188
47. Grafakos 2004
48. Grafakos & Teschl 2013
49. More generally, one can take a sequence of functions that are in the intersection of L¹ and L² and that converges to f in the L²-norm, and define the Fourier transform of f as the L² -limit of the Fourier transforms of these functions.
50. "Applied Fourier Analysis and Elements of Modern Signal Processing Lecture 3" (PDF). January 12, 2016. Retrieved 2019-10-11.
51. Stein & Weiss 1971, Thm. 2.3
52. Pinsky 2002, p. 256
53. Hewitt & Ross 1970, Chapter 8
54. Knapp 2001
55. Correia, L. B.; Justo, J. F.; Angélico, B. A. (2024). "Polynomial Adaptive Synchrosqueezing Fourier Transform: A method to optimize multiresolution". Digital Signal Processing. 150: 104526. doi:10.1016/j.dsp.2024.104526.
56. Gradshteyn et al. 2015
57. Press et al. 1992
58. Bailey & Swarztrauber 1994
59. Lado 1971
60. Simonen & Olkkonen 1985
61. "The Integration Property of the Fourier Transform". The Fourier Transform .com. 2015 [2010]. Archived from the original on 2022-01-26. Retrieved 2023-08-20.
62. Stein & Weiss 1971, Thm. IV.3.3
63. Easton 2010
64. Stein & Weiss 1971, Thm. 4.15
65. Stein & Weiss 1971, p. 6

References

• Arfken, George (1985), Mathematical Methods for Physicists (3rd ed.), Academic Press, ISBN 9780120598205
• Bailey, David H.; Swarztrauber, Paul N. (1994), "A fast method for the numerical evaluation of continuous Fourier and Laplace transforms" (PDF), SIAM Journal on Scientific Computing, 15 (5): 1105–1110, Bibcode:1994SJSC...15.1105B, CiteSeerX 10.1.1.127.1534, doi:10.1137/0915067, archived from the original (PDF) on 2008-07-20, retrieved 2017-11-01
• Boashash, B., ed. (2003), Time–Frequency Signal Analysis and Processing: A Comprehensive Reference, Oxford: Elsevier Science, ISBN 978-0-08-044335-5
• Bochner, S.; Chandrasekharan, K. (1949), Fourier Transforms, Princeton University Press
• Bracewell, R. N. (2000), The Fourier Transform and Its Applications (3rd ed.), Boston: McGraw-Hill, ISBN 978-0-07-116043-8
• Campbell, George; Foster, Ronald (1948), Fourier Integrals for Practical Applications, New York: D. Van Nostrand Company, Inc.
• Celeghini, Enrico; Gadella, Manuel; del Olmo, Mariano A. (2021), "Hermite Functions and Fourier Series", Symmetry, 13 (5): 853, arXiv:2007.10406, Bibcode:2021Symm...13..853C, doi:10.3390/sym13050853
• Champeney, D.C. (1987), A Handbook of Fourier Theorems, Cambridge University Press
• Chatfield, Chris (2004), The Analysis of Time Series: An Introduction, Texts in Statistical Science (6th ed.), London: Chapman & Hall/CRC, ISBN 9780203491683
• Clozel, Laurent; Delorme, Patrice (1985), "Sur le théorème de Paley-Wiener invariant pour les groupes de Lie réductifs réels", Comptes Rendus de l'Académie des Sciences, Série I, 300: 331–333
• Condon, E. U. (1937), "Immersion of the Fourier transform in a continuous group of functional transformations", Proc. Natl. Acad. Sci., 23 (3): 158–164, Bibcode:1937PNAS...23..158C, doi:10.1073/pnas.23.3.158, PMC 1076889, PMID 16588141
• de Groot, Sybren R.; Mazur, Peter (1984), Non-Equilibrium Thermodynamics (2nd ed.), New York: Dover
• Duoandikoetxea, Javier (2001), Fourier Analysis, American Mathematical Society, ISBN 978-0-8218-2172-5
• Dym, H.; McKean, H. (1985), Fourier Series and Integrals, Academic Press, ISBN 978-0-12-226451-1
• Easton, Roger L. Jr. (2010), Fourier Methods in Imaging, John Wiley & Sons, ISBN 978-0-470-68983-7, retrieved 26 May 2020
• Erdélyi, Arthur, ed. (1954), Tables of Integral Transforms, vol. 1, McGraw-Hill
• Feller, William (1971), An Introduction to Probability Theory and Its Applications, vol. II (2nd ed.), New York: Wiley, MR 0270403
• Folland, Gerald (1989), Harmonic analysis in phase space, Princeton University Press
• Folland, Gerald (1992), Fourier analysis and its applications, Wadsworth & Brooks/Cole
• Fourier, J.B. Joseph (1822), Théorie analytique de la chaleur (in French), Paris: Firmin Didot, père et fils, OCLC 2688081
• Fourier, J.B. Joseph (1878) [1822], The Analytical Theory of Heat, translated by Alexander Freeman, The University Press (translated from French)
• Gradshteyn, Izrail Solomonovich; Ryzhik, Iosif Moiseevich; Geronimus, Yuri Veniaminovich; Tseytlin, Michail Yulyevich; Jeffrey, Alan (2015), Zwillinger, Daniel; Moll, Victor Hugo (eds.), Table of Integrals, Series, and Products, translated by Scripta Technica, Inc. (8th ed.), Academic Press, ISBN 978-0-12-384933-5
• Grafakos, Loukas (2004), Classical and Modern Fourier Analysis, Prentice-Hall, ISBN 978-0-13-035399-3
• Grafakos, Loukas; Teschl, Gerald (2013), "On Fourier transforms of radial functions and distributions", J. Fourier Anal. Appl., 19: 167–179, arXiv:1112.5469, doi:10.1007/s00041-012-9242-5, S2CID 1280745
• Greiner, W.; Reinhardt, J. (1996), Field Quantization, Springer, ISBN 978-3-540-59179-5
• Gelfand, I.M.; Shilov, G.E. (1964), Generalized Functions, vol. 1, New York: Academic Press (translated from Russian)
• Gelfand, I.M.; Vilenkin, N.Y. (1964), Generalized Functions, vol. 4, New York: Academic Press (translated from Russian)
• Hewitt, Edwin; Ross, Kenneth A. (1970), Abstract harmonic analysis, Die Grundlehren der mathematischen Wissenschaften, Band 152, vol. II: Structure and analysis for compact groups. Analysis on locally compact Abelian groups, Springer, MR 0262773
• Hörmander, L. (1976), Linear Partial Differential Operators, vol. 1, Springer, ISBN 978-3-540-00662-6
• Howe, Roger (1980), "On the role of the Heisenberg group in harmonic analysis", Bulletin of the American Mathematical Society, 3 (2): 821–844, doi:10.1090/S0273-0979-1980-14825-9, MR 0578375
• James, J.F. (2011), A Student's Guide to Fourier Transforms (3rd ed.), Cambridge University Press, ISBN 978-0-521-17683-5
• Jordan, Camille (1883), Cours d'Analyse de l'École Polytechnique, vol. II, Calcul Intégral: Intégrales définies et indéfinies (2nd ed.), Paris{{citation}}: CS1 maint: location missing publisher (link)
• Kaiser, Gerald (1994), "A Friendly Guide to Wavelets", Physics Today, 48 (7): 57–58, Bibcode:1995PhT....48g..57K, doi:10.1063/1.2808105, ISBN 978-0-8176-3711-8
• Kammler, David (2000), A First Course in Fourier Analysis, Prentice Hall, ISBN 978-0-13-578782-3
• Katznelson, Yitzhak (1976), An Introduction to Harmonic Analysis, Dover, ISBN 978-0-486-63331-2
• Khare, Kedar; Butola, Mansi; Rajora, Sunaina (2023), "Chapter 2.3 Fourier Transform as a Limiting Case of Fourier Series", Fourier Optics and Computational Imaging (2nd ed.), Springer, doi:10.1007/978-3-031-18353-9, ISBN 978-3-031-18353-9, S2CID 255676773
• Kirillov, Alexandre; Gvishiani, Alexei D. (1982) [1979], Theorems and Problems in Functional Analysis, Springer (translated from Russian)
• Knapp, Anthony W. (2001), Representation Theory of Semisimple Groups: An Overview Based on Examples, Princeton University Press, ISBN 978-0-691-09089-4
• Kolmogorov, Andrey Nikolaevich; Fomin, Sergei Vasilyevich (1999) [1957], Elements of the Theory of Functions and Functional Analysis, Dover (translated from Russian)
• Lado, F. (1971), "Numerical Fourier transforms in one, two, and three dimensions for liquid state calculations", Journal of Computational Physics, 8 (3): 417–433, Bibcode:1971JCoPh...8..417L, doi:10.1016/0021-9991(71)90021-0
• Müller, Meinard (2015), The Fourier Transform in a Nutshell. (PDF), Springer, doi:10.1007/978-3-319-21945-5, ISBN 978-3-319-21944-8, S2CID 8691186, archived from the original (PDF) on 2016-04-08, retrieved 2016-03-28; also available at Fundamentals of Music Processing, Section 2.1, pages 40–56
• Oppenheim, Alan V.; Schafer, Ronald W.; Buck, John R. (1999), Discrete-time signal processing (2nd ed.), Upper Saddle River, N.J.: Prentice Hall, ISBN 0-13-754920-2
• Paley, R.E.A.C.; Wiener, Norbert (1934), Fourier Transforms in the Complex Domain, American Mathematical Society Colloquium Publications, Providence, Rhode Island: American Mathematical Society
• Pinsky, Mark (2002), Introduction to Fourier Analysis and Wavelets, Brooks/Cole, ISBN 978-0-534-37660-4
• Poincaré, Henri (1895), Théorie analytique de la propagation de la chaleur, Paris: Carré
• Polyanin, A. D.; Manzhirov, A. V. (1998), Handbook of Integral Equations, Boca Raton: CRC Press, ISBN 978-0-8493-2876-3
• Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T. (1992), Numerical Recipes in C: The Art of Scientific Computing, Second Edition (2nd ed.), Cambridge University Press
• Proakis, John G.; Manolakis, Dimitri G. (1996). Digital Signal Processing: Principles, Algorithms and Applications (3 ed.). New Jersey: Prentice-Hall International. Bibcode:1996dspp.book.....P. ISBN 9780133942897. sAcfAQAAIAAJ.
• Rahman, Matiur (2011), Applications of Fourier Transforms to Generalized Functions, WIT Press, ISBN 978-1-84564-564-9
• Rudin, Walter (1987), Real and Complex Analysis (3rd ed.), Singapore: McGraw Hill, ISBN 978-0-07-100276-9
• Simonen, P.; Olkkonen, H. (1985), "Fast method for computing the Fourier integral transform via Simpson's numerical integration", Journal of Biomedical Engineering, 7 (4): 337–340, doi:10.1016/0141-5425(85)90067-6, PMID 4057997
• Smith, Julius O. "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition". ccrma.stanford.edu. Retrieved 2022-12-29. We may think of a real sinusoid as being the sum of a positive-frequency and a negative-frequency complex sinusoid.
• Stein, Elias; Shakarchi, Rami (2003), Fourier Analysis: An introduction, Princeton University Press, ISBN 978-0-691-11384-5
• Stein, Elias; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton, N.J.: Princeton University Press, ISBN 978-0-691-08078-9
• Taneja, H.C. (2008), "Chapter 18: Fourier integrals and Fourier transforms", Advanced Engineering Mathematics, vol. 2, New Delhi, India: I. K. International Pvt Ltd, ISBN 978-8189866563
• Titchmarsh, E. (1986) [1948], Introducción a la teoría de las integrales de Fourier (2.ª ed.), Universidad de Oxford: Clarendon Press , ISBN 978-0-8284-0324-5
• Vretblad, Anders (2000), Análisis de Fourier y sus aplicaciones , Textos de posgrado en matemáticas , vol. 223, Nueva York: Springer , ISBN 978-0-387-00836-3
• Whittaker, ET ; Watson, GN (1927), Un curso de análisis moderno (4.ª ed.), Cambridge University Press
• Widder, David Vernon; Wiener, Norbert (agosto de 1938), "Observaciones sobre la fórmula de inversión clásica para la integral de Laplace", Boletín de la Sociedad Matemática Americana , 44 (8): 573–575, doi :10.1090/s0002-9904-1938-06812-7
• Wiener, Norbert (1949), Extrapolación, interpolación y suavizado de series temporales estacionarias con aplicaciones de ingeniería , Cambridge, Mass.: Technology Press y John Wiley & Sons y Chapman & Hall
• Wilson, RG (1995), Series de Fourier y técnicas de transformada óptica en óptica contemporánea , Nueva York: Wiley , ISBN 978-0-471-30357-2
• Wolf, Kurt B. (1979), Transformadas integrales en ciencia e ingeniería, Springer , doi :10.1007/978-1-4757-0872-1, ISBN 978-1-4757-0874-5
• Yosida, K. (1968), Análisis funcional , Springer , ISBN 978-3-540-58654-8

Enlaces externos

• Medios relacionados con la transformación de Fourier en Wikimedia Commons
• Enciclopedia de Matemáticas
• Weisstein, Eric W. "Transformada de Fourier". MundoMatemático .
• Transformada de Fourier en cristalografía