
El análisis espectral de mínimos cuadrados ( LSSA ) es un método para estimar un espectro de frecuencia basado en un ajuste de mínimos cuadrados de sinusoides a muestras de datos, similar al análisis de Fourier . [1] [2] El análisis de Fourier, el método espectral más utilizado en la ciencia, generalmente aumenta el ruido periódico largo en los registros largos y con espacios; LSSA mitiga tales problemas. [3] A diferencia del análisis de Fourier, no es necesario que los datos estén igualmente espaciados para utilizar LSSA.
Desarrollado en 1969 [4] y 1971, [5] LSSA también se conoce como método de Vaníček y método de Gauss-Vaniček en honor a Petr Vaníček , [6] [7] y como método de Lomb [3] o periodograma de Lomb-Scargle. , [2] [8] basado en las simplificaciones primero de Nicholas R. Lomb [9] y luego de Jeffrey D. Scargle. [10]
Las estrechas conexiones entre el análisis de Fourier , el periodograma y el ajuste de mínimos cuadrados de las sinusoides se conocen desde hace mucho tiempo. [11] Sin embargo, la mayoría de los desarrollos se limitan a conjuntos de datos completos de muestras igualmente espaciadas. En 1963, Freek JM Barning de Mathematisch Centrum , Amsterdam, manejó datos espaciados desigualmente mediante técnicas similares, [12] incluyendo un análisis de periodograma equivalente a lo que hoy se llama método de Lomb y un ajuste de mínimos cuadrados de frecuencias seleccionadas de sinusoides determinadas a partir de tales periodogramas, y conectados mediante un procedimiento conocido hoy como búsqueda de coincidencia con ajuste post-back [13] o búsqueda de coincidencia ortogonal. [14]
Petr Vaníček , geofísico y geodesista canadiense de la Universidad de New Brunswick , propuso en 1969 también el enfoque de búsqueda de coincidencias para datos igualmente y desigualmente espaciados, al que llamó "análisis espectral sucesivo" y al resultado un "periodograma de mínimos cuadrados". [4] Generalizó este método para tener en cuenta cualquier componente sistemático más allá de una media simple, como una "tendencia secular lineal (cuadrática, exponencial,...) prevista de magnitud desconocida", y lo aplicó a una variedad de muestras, en 1971. [5]
El método de mínimos cuadrados estricto de Vaníček fue simplificado en 1976 por Nicholas R. Lomb de la Universidad de Sydney , quien señaló su estrecha conexión con el análisis de periodograma . [9] Posteriormente, la definición de periodograma de datos desigualmente espaciados fue modificada y analizada por Jeffrey D. Scargle del Centro de Investigación Ames de la NASA , [10] quien demostró que, con cambios menores, se vuelve idéntica a la fórmula de mínimos cuadrados de Lomb para Ajuste de frecuencias sinusoides individuales.
Scargle afirma que su artículo "no introduce una nueva técnica de detección, sino que estudia la confiabilidad y eficiencia de la detección con la técnica más comúnmente utilizada, el periodograma, en el caso en que los tiempos de observación no están espaciados uniformemente ", y señala además con respecto a ajuste de mínimos cuadrados de sinusoides en comparación con el análisis de periodograma, que su artículo "establece, aparentemente por primera vez, que (con las modificaciones propuestas) estos dos métodos son exactamente equivalentes". [10]
Press [3] resume el desarrollo de esta manera:
Lomb desarrolló un método completamente diferente de análisis espectral para datos muestreados de manera desigual, uno que mitiga estas dificultades y tiene algunas otras propiedades muy deseables, basado en parte en trabajos anteriores de Barning y Vanicek, y además elaborado por Scargle.
En 1989, Michael J. Korenberg de la Universidad Queen en Kingston, Ontario, desarrolló el método de "búsqueda ortogonal rápida" para encontrar más rápidamente una descomposición casi óptima de espectros u otros problemas, [15] similar a la técnica que más tarde se conoció como la búsqueda de emparejamiento ortogonal.
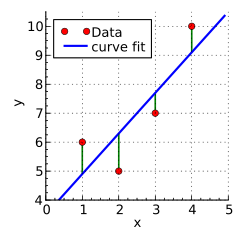
En el método de Vaníček, un conjunto de datos discretos se aproxima mediante una suma ponderada de sinusoides de frecuencias determinadas progresivamente mediante una regresión lineal estándar o un ajuste de mínimos cuadrados . [16] Las frecuencias se eligen utilizando un método similar al de Barning, pero yendo más allá al optimizar la elección de cada nueva frecuencia sucesiva eligiendo la frecuencia que minimice el residuo después del ajuste de mínimos cuadrados (equivalente a la técnica de ajuste ahora conocida como búsqueda de emparejamiento). con preequipamiento [13] ). El número de sinusoides debe ser menor o igual al número de muestras de datos (contando los senos y cosenos de la misma frecuencia como sinusoides separados).
Un vector de datos Φ se representa como una suma ponderada de funciones de base sinusoidal, tabuladas en una matriz A evaluando cada función en los tiempos de muestra, con el vector de peso x :
donde el vector de pesos x se elige para minimizar la suma de errores al cuadrado al aproximar Φ . La solución para x es de forma cerrada, utilizando regresión lineal estándar : [17]
Aquí la matriz A puede basarse en cualquier conjunto de funciones mutuamente independientes (no necesariamente ortogonales) cuando se evalúan en los tiempos de muestra; Las funciones utilizadas para el análisis espectral suelen ser senos y cosenos distribuidos uniformemente en el rango de frecuencia de interés. Si elegimos demasiadas frecuencias en un rango de frecuencias demasiado estrecho, las funciones no serán lo suficientemente independientes, la matriz estará mal condicionada y el espectro resultante carecerá de significado. [17]
Cuando las funciones base en A son ortogonales (es decir, no correlacionadas, lo que significa que las columnas tienen productos escalares por pares cero ), la matriz A T A es diagonal; cuando todas las columnas tienen la misma potencia (suma de cuadrados de elementos), entonces esa matriz es una matriz identidad multiplicada por una constante, por lo que la inversión es trivial. Este último es el caso cuando los tiempos de muestra están igualmente espaciados y las sinusoides se eligen como senos y cosenos igualmente espaciados en pares en el intervalo de frecuencia 0 a medio ciclo por muestra (espaciados por 1/N ciclos por muestra, omitiendo las fases sinusoidales en 0 y frecuencia máxima donde son idénticamente cero). Este caso se conoce como transformada discreta de Fourier , ligeramente reescrita en términos de medidas y coeficientes. [17]
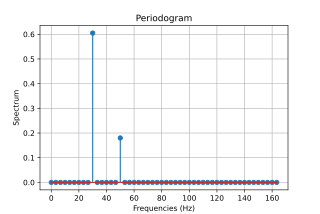
Al intentar reducir la carga computacional del método Vaníček en 1976 [9] (ya no es un problema), Lomb propuso usar la simplificación anterior en general, excepto para las correlaciones por pares entre bases seno y coseno de la misma frecuencia, ya que las correlaciones entre pares de sinusoides suelen ser pequeños, al menos cuando no están muy espaciados. Esta formulación es esencialmente la del periodograma tradicional , pero adaptada para su uso con muestras espaciadas de manera desigual. El vector x es una estimación razonablemente buena de un espectro subyacente, pero como ignoramos cualquier correlación, A x ya no es una buena aproximación a la señal y el método ya no es un método de mínimos cuadrados; ser referido como tal.
En lugar de simplemente tomar productos escalares de los datos con formas de onda seno y coseno directamente, Scargle modificó la fórmula del periodograma estándar para encontrar primero un retraso de tiempo, de modo que este par de sinusoides fuera mutuamente ortogonal en tiempos de muestra y también se ajustara para los tiempos potencialmente desiguales. potencias de estas dos funciones básicas, para obtener una mejor estimación de la potencia a una frecuencia. [3] [10] Este procedimiento hizo que su método de periodograma modificado fuera exactamente equivalente al método de Lomb. El retraso de tiempo por definición es igual a
Entonces el periodograma en frecuencia se estima como:
que, como informa Scargle, tiene la misma distribución estadística que el periodograma en el caso de muestra uniforme. [10]
En cualquier frecuencia individual , este método proporciona la misma potencia que un ajuste de mínimos cuadrados para sinusoides de esa frecuencia y de la forma:
En la práctica, siempre es difícil juzgar si un pico de Lomb determinado es significativo o no, especialmente cuando se desconoce la naturaleza del ruido, por lo que, por ejemplo, un pico espectral de falsa alarma en el análisis del periodograma de Lomb de una señal periódica ruidosa puede resultar de ruido en datos de turbulencia. [19] Los métodos de Fourier también pueden informar picos espectrales falsos cuando se analizan datos parcheados o editados de otra manera. [7]
El periodograma estándar de Lomb-Scargle solo es válido para un modelo con media cero. Por lo general, esto se aproxima: restando la media de los datos antes de calcular el periodograma. Sin embargo, esta es una suposición inexacta cuando la media del modelo (las sinusoides ajustadas) es distinta de cero. El periodograma generalizado de Lomb-Scargle elimina esta suposición y resuelve explícitamente la media. En este caso, la función instalada es
El periodograma generalizado de Lomb-Scargle también se ha denominado en la literatura periodograma medio flotante . [21]
Michael Korenberg, de la Queen's University en Kingston, Ontario , desarrolló un método para elegir un conjunto disperso de componentes de un conjunto demasiado completo, como componentes sinusoidales para análisis espectral, llamado búsqueda ortogonal rápida (FOS). Matemáticamente, FOS utiliza una descomposición de Cholesky ligeramente modificada en un proceso de reducción del error cuadrático medio (MSER), implementado como una inversión de matriz dispersa . [15] [22] Al igual que con los otros métodos LSSA, FOS evita la principal deficiencia del análisis discreto de Fourier, por lo que puede identificar con precisión periodicidades incrustadas y sobresalir con datos espaciados de manera desigual. El método de búsqueda ortogonal rápida se aplicó también a otros problemas, como la identificación de sistemas no lineales .
Palmer ha desarrollado un método para encontrar la función que mejor se ajuste a cualquier número elegido de armónicos, lo que permite una mayor libertad para encontrar funciones armónicas no sinusoidales. [23] La suya es una técnica rápida ( basada en FFT ) para el análisis de mínimos cuadrados ponderados en datos espaciados arbitrariamente con errores estándar no uniformes. El código fuente que implementa esta técnica está disponible. [24] Debido a que los datos a menudo no se muestrean en tiempos discretos espaciados uniformemente, este método "cuadricula" los datos llenando escasamente una matriz de series de tiempo en los tiempos de muestreo. Todos los puntos de la cuadrícula que intervienen reciben un peso estadístico cero, lo que equivale a tener infinitas barras de error en momentos entre muestras.
La característica más útil de LSSA es permitir el análisis espectral de registros incompletos , sin la necesidad de manipular datos o inventar datos que de otro modo no existirían.
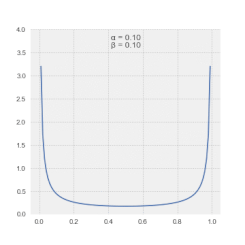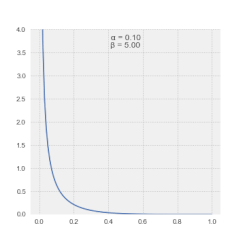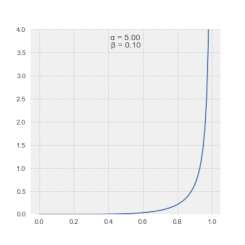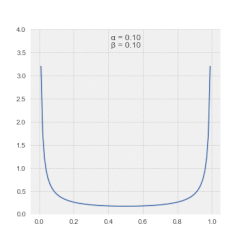
Las magnitudes en el espectro LSSA representan la contribución de una frecuencia o período a la varianza de la serie temporal . [4] Generalmente, las magnitudes espectrales así definidas permiten un régimen de nivel de significancia sencillo de la salida . [25] Alternativamente, las magnitudes espectrales en el espectro de Vaníček también se pueden expresar en dB . [26] Tenga en cuenta que las magnitudes espectrales en el espectro de Vaníček siguen la distribución β . [27]
Es posible la transformación inversa del LSSA de Vaníček, como se ve más fácilmente escribiendo la transformación directa como una matriz; la matriz inversa (cuando la matriz no es singular) o pseudoinversa será entonces una transformación inversa; lo inverso coincidirá exactamente con los datos originales si las sinusoides elegidas son mutuamente independientes en los puntos de muestra y su número es igual al número de puntos de datos. [17] No se conoce ningún procedimiento inverso de este tipo para el método del periodograma.
El LSSA se puede implementar en menos de una página de código MATLAB . [28] En esencia: [16]
"para calcular el espectro de mínimos cuadrados debemos calcular m valores espectrales... lo que implica realizar la aproximación de mínimos cuadrados m veces, cada vez para obtener [la potencia espectral] para una frecuencia diferente"
Es decir, para cada frecuencia en un conjunto de frecuencias deseado, se evalúan las funciones seno y coseno en los tiempos correspondientes a las muestras de datos, y se toman y normalizan apropiadamente los productos escalares del vector de datos con los vectores sinusoides; siguiendo el método conocido como periodograma de Lomb/Scargle, se calcula un desplazamiento de tiempo para cada frecuencia para ortogonalizar los componentes seno y coseno antes del producto escalar; [17] finalmente, se calcula una potencia a partir de esos dos componentes de amplitud . Este mismo proceso implementa una transformada de Fourier discreta cuando los datos están espaciados uniformemente en el tiempo y las frecuencias elegidas corresponden a números enteros de ciclos sobre el registro de datos finito.
Este método trata cada componente sinusoidal de forma independiente o fuera de contexto, aunque no sean ortogonales a los puntos de datos; es el método original de Vaníček. Además, es posible realizar un ajuste de mínimos cuadrados simultáneo o en contexto resolviendo una ecuación matricial y dividiendo la varianza total de los datos entre las frecuencias sinusoides especificadas. [17] Esta solución matricial de mínimos cuadrados está disponible de forma nativa en MATLAB como operador de barra invertida . [29]
Además, el método simultáneo o en contexto, a diferencia de la versión independiente o fuera de contexto (así como la versión de periodograma debido a Lomb), no puede ajustar más componentes (senos y cosenos) que muestras de datos, por lo que que: [17]
"...también pueden surgir graves repercusiones si las frecuencias seleccionadas dan como resultado que algunos de los componentes de Fourier (funciones trigonométricas) se vuelvan casi linealmente dependientes entre sí, produciendo así un N mal condicionado o casi singular. Para evitar tal mal condicionamiento, se convierte en Es necesario seleccionar un conjunto diferente de frecuencias a estimar (por ejemplo, frecuencias equiespaciadas) o simplemente ignorar las correlaciones en N (es decir, los bloques fuera de la diagonal) y estimar la transformada de mínimos cuadrados inversa por separado para las frecuencias individuales... "
El método del periodograma de Lomb, por otro lado, puede utilizar un número arbitrariamente alto o una densidad de componentes de frecuencia, como en un periodograma estándar ; es decir, el dominio de la frecuencia puede sobremuestrearse mediante un factor arbitrario. [3] Sin embargo, como se mencionó anteriormente, se debe tener en cuenta que la simplificación de Lomb y su desviación del criterio de mínimos cuadrados abrió su técnica a graves fuentes de errores, resultando incluso en picos espectrales falsos. [19]
En el análisis de Fourier, como la transformada de Fourier y la transformada discreta de Fourier , las sinusoides ajustadas a los datos son todas mutuamente ortogonales, por lo que no hay distinción entre la simple proyección fuera de contexto basada en productos escalares sobre funciones base versus una proyección integrada. contexto de ajuste simultáneo de mínimos cuadrados; es decir, no se requiere inversión de matrices para dividir por mínimos cuadrados la varianza entre sinusoides ortogonales de diferentes frecuencias. [30] En el pasado, el método de Fourier era para muchos el método elegido gracias a su rápida implementación de la transformada de Fourier , eficiente en el procesamiento , cuando estaban disponibles registros de datos completos con muestras igualmente espaciadas, y también utilizaron la familia de técnicas de Fourier para analizar registros con espacios. , que, sin embargo, requirió manipular e incluso inventar datos inexistentes para poder ejecutar un algoritmo basado en Fourier.