Flujo de acortamiento de una curva
Pierde área a un ritmo constante, y su perímetro disminuye lo más rápido posible para cualquier evolución de curva continua.
El círculo es la única curva cerrada simple que mantiene su forma bajo el proceso de flujo de acortamiento, pero algunas curvas que se cruzan entre sí o tienen una longitud infinita mantienen su forma, incluida la curva de la parca, una curva infinita que se traslada hacia arriba, así como las espirales que giran sobre sí mismas manteniendo el mismo tamaño y forma.
[3] Debido a que los elementos de esta ecuación, la longitud del arco, la curvatura y el tiempo, no se ven afectados por las traslaciones y rotaciones del plano euclídeo, se deduce que el flujo definido por esta ecuación es invariante bajo traslaciones y rotaciones (o más precisamente, se puede afirmar que es equivariante).
[7] El seno del topólogo es un ejemplo que instantáneamente se vuelve suave, a pesar de no ser siquiera localmente conexa.
Las curvas en el espacio pueden cruzarse con otras o consigo mismas de acuerdo con este flujo, y el flujo puede conducir a singularidades en las curvas; con la condición de que toda singularidad es asintótica a un plano.
[12] Es posible extender la definición del flujo a entidades más generales que las curvas, lo que se puede comprobar utilizando varivariedades rectificables o el método del conjunto de nivel.
[14] Si dos curvas simples cerradas suaves disjuntas experimentan el flujo de acortamiento de la curva simultáneamente, permanecen disjuntas a medida que avanza el flujo.
La razón es que, si dos curvas suaves se mueven de una manera que crean un cruce, entonces, en el momento del primer cruce, las curvas serían necesariamente tangentes entre sí, sin cruzarse.
Porque, si una curva suave dada C está rodeada por una circunferencia, ambas permanecerán disjuntas mientras existan.
El integrando siempre es no negativo, y para cualquier curva cerrada suave existen arcos dentro de los cuales es estrictamente positivo, por lo que la longitud disminuye monótonamente.
[17] Debido a que el área de una curva se reduce a una tasa constante, y (por isoperimetría) un círculo tiene el área más grande posible entre las curvas cerradas simples de una longitud dada, se deduce que las circunferencias son las curvas más lentas en colapsar hasta un punto bajo el flujo de acortamiento.
Todas las demás curvas tardan menos en contraerse que una circunferencia de la misma longitud.
Por lo tanto, la curvatura absoluta total nunca puede aumentar a medida que evoluciona la curva.
[24] Este resultado se debe a Michael Gage, Richard Hamilton y Matthew Grayson.
Gage demostró la convergencia a una circunferencia para curvas convexas que se contraen en un punto.
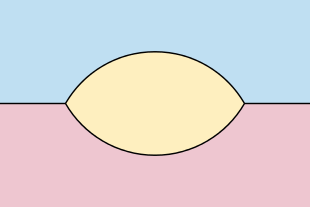
[28] Para redes formadas por dos rayos disjuntos en la misma línea, junto con dos curvas suaves que conectan los extremos de los dos rayos, se cumple un análogo del teorema de Gage-Hamilton-Grayson, según el cual la región entre las dos curvas se vuelve convexa y luego converge a una forma de "vesica piscis" (mandorla).
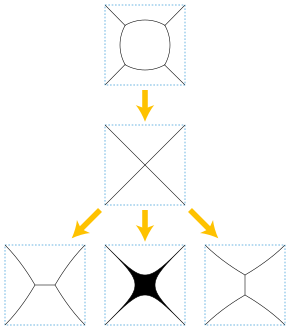
Por ejemplo, si una lemniscata (cualquier curva inmersa suave con un solo cruce, parecida a la figura de un 8 o al símbolo de infinito) tiene áreas desiguales en sus dos lóbulos, finalmente el lóbulo más pequeño colapsará en un punto.
Cuando un bucle colapsa en una singularidad, la cantidad de curvatura absoluta total que se pierde es al menos 2Π o exactamente Π.
[30] En una variedad de Riemann, cualquier curva cerrada simple suave seguirá siendo suave y simple a medida que evoluciona, al igual que en el caso euclidiano.
En este último caso, la curva necesariamente converge a una geodésica cerrada de la superficie.
[34] Debido a que todas las demás curvas cerradas simples convergen en una circunferencia, la circunferencia es precisamente la única curva cerrada simple que mantiene su forma bajo el flujo de acortamiento.
Sin embargo, hay muchos otros ejemplos de curvas que no son simples (incluyen cruces automáticos) o no están cerradas (se extienden hasta el infinito) y mantienen su forma.
Todas las soluciones autosimilares que se encogen o mantienen el mismo tamaño en lugar de crecer son soluciones antecedentes en este sentido; se pueden extrapolar hacia atrás invirtiendo la transformación autosimilar que experimentarán por el flujo de acortamiento de la curva hacia adelante.
El método de las diferencias finitas se usa para obtener fórmulas con las que calcular el vector normal aproximado y la curvatura en cada vértice del polígono, y estos valores se usan para determinar cómo mover cada vértice en cada paso de tiempo.
[49] Otro método de diferenciación finita por Crandall y Lions (1996) modifica la fórmula para la curvatura en cada vértice al agregarle un término pequeño basado en un operador laplaciano.
Esta modificación se llama regularización elíptica y puede usarse para ayudar a probar la existencia de flujos generalizados, así como en su simulación numérica.
[50] Usándolo, se puede demostrar que el método de Crandall y Lions converge y es el único método numérico enumerado por Cao que está equipado con límites en su tasa de convergencia.
Mokhtarian y Mackworth (1992) sugiere un método numérico para calcular una aproximación al flujo de acortamiento de la curva que mantiene una aproximación discreta a la curva y alterna entre dos pasos: Merriman, Bence y Osher (1992) describe un procedimiento que opera en una cuadrícula cuadrada bidimensional, en la práctica una matriz de píxeles.
Esta representación se actualiza alternando dos pasos: Para que este esquema sea preciso, el paso de tiempo debe ser lo suficientemente grande como para hacer que la curva se mueva al menos un píxel incluso en puntos de baja curvatura, pero lo suficientemente pequeño como para hacer que el radio de desenfoque sea menor que el radio mínimo de curvatura.
Es posible usar núcleos distintos a la función del calor, o refinar adaptativamente la cuadrícula para que tenga alta resolución cerca de la curva pero no pierda tiempo y memoria en píxeles situados lejos de la curva que no contribuyen al resultado.