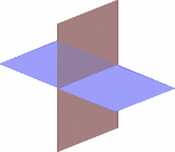
Plano (geometría)
Se denomina frontera, borde u origen del semiplano.
Los planos son especialmente utilizados en ingeniería, arquitectura y diseño, ya que sirven para diagramar en una superficie plana o en otras superficies que son regularmente tridimensionales.
Consecuentemente, el sistema cartesiano establece una correspondencia biunívoca entre un concepto geométrico como es el de los puntos del plano y un concepto algebraico como son los pares ordenados de números.
Ocasionalmente se usa el término "área" como sinónimo de superficie, cuando no existe confusión entre el concepto geométrico en sí mismo (superficie) y la magnitud métrica asociada al concepto geométrico (área).
Cada línea de referencia se llama eje de coordenadas o simplemente eje del sistema, y el punto donde se encuentran es su origen', normalmente en el par ordenado (0, 0).
Las coordenadas también pueden definirse como las posiciones de las proyecciones perpendiculares del punto sobre los dos ejes, expresadas como distancias con signo desde el origen.
Estos comentaristas introdujeron varios conceptos al tiempo que intentaban aclarar las ideas contenidas en la obra de Descartes.
[2] Más tarde, se pensó en el plano como un campo, en el que dos puntos cualesquiera podían multiplicarse y, excepto 0, dividirse.
Estos reciben su nombre de Jean-Robert Argand (1768-1822), aunque fueron descritos por primera vez por el topógrafo y matemático danés-noruego Caspar Wessel (1745-1818).
Los planos euclídeos surgen a menudo como subespacios del espacio tridimensional.
A continuación se muestran los primeros regulares: El símbolo de Schläfli
El monógono (o henágono) regular {1} y el digon regular {2} {2} pueden considerarse polígonos regulares degenerados y existen de forma no degenerada en espacios no euclidianos como una 2-esfera, un 2-toro, o un cilindro circular recto.
Existen infinitos polígonos regulares no convexos en dos dimensiones, cuyos símbolos de Schläfli consisten en números racionales {n/m}.
La hiperesfera en 2 dimensiones es un círculo, a veces llamado 1-esfera (S1) porque es un colector unidimensional.
Existen infinidad de otras formas curvas en dos dimensiones, entre las que destacan las secciones cónicas: la elipse, la parábola y la hipérbola.
En un espacio euclidiano tridimensional ℝ3, podemos hallar los siguientes hechos (los cuales no son necesariamente válidos para dimensiones mayores): Un plano queda definido por los siguientes elementos geométricos: un punto y dos vectores: Punto P = (x1, y1, z1)Vector u = (ux, uy, uz)Vector v = (a2, b2, c2) donde
De esta manera la ecuación del plano es: Donde (A, B, C) es un vector perpendicular al plano y coincide con el producto vectorial de los vectores u y v.
La fórmula para hallar la ecuación cuando no está en el origen es: P = P0 + mA + nB es la ecuación del plano determinado por un punto fijo y dos vectores A y B no colineales.
[4] a.x = 0, donde a es un vector ortogonal y x un punto del plano.
, entonces la fórmula anterior de la distancia D se reduce a: Se llama semiplano, en geometría, cada una de las dos partes en que un plano queda dividido por una recta.
En cada pareja de semiplanos que una recta r determina sobre un plano existen infinitos puntos tales que: En topología, el plano se caracteriza por ser el único espacio contráctil bidimensional.
Su dimensión se caracteriza por el hecho de que la eliminación de un punto del plano deja un espacio que está conectado, pero no simplemente conectado.