Parábola (matemática)
En geometría proyectiva, la parábola se define como la curva envolvente de las rectas que unen pares de puntos homólogos en una proyectividad semejante o semejanza.
Por ejemplo, son parábolas las trayectorias ideales de los cuerpos que se mueven bajo la influencia exclusiva de la gravedad (ver movimiento parabólico y trayectoria balística).
Es Apolonio quien menciona que un espejo parabólico refleja de forma paralela los rayos emitidos desde su foco, propiedad usada hoy en día en las antenas satelitales.
La parábola también fue estudiada por Arquímedes, nuevamente en la búsqueda de una solución para un problema famoso: la cuadratura del círculo, dando como resultado el libro Sobre la cuadratura de la parábola.
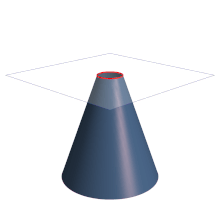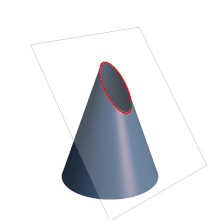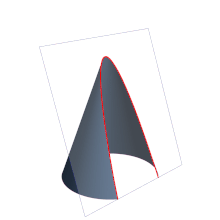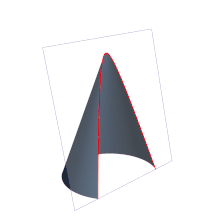
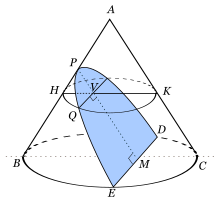
Aunque la identificación de parábola con la intersección entre un cono recto y un plano que forme un ángulo con el eje de revolución del cono igual al que presenta su generatriz es exacta, es común definirla también como un lugar geométrico: Se denomina parábola al lugar geométrico de un punto que se mueve en un plano de tal manera que equidista de una recta fija, llamada directriz y de un punto fijo en el plano, que no pertenece a la parábola ni a la directriz, llamado foco.
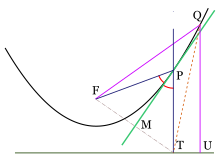
De esta forma, una vez fijados una recta y un punto se puede construir una parábola que los tenga por directriz y foco respectivamente, usando el siguiente procedimiento: Se toma un punto
cualquiera de la recta, se lo une con el foco dado
y a continuación se traza la mediatriz (o perpendicular por el punto medio) del segmento
se pueden hallar tantos puntos de la parábola como sea necesario.
sean cuadrados, junto con la construcción mencionada en la sección anterior.
La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.
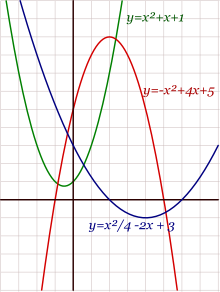
Desafortunadamente, al estudiar analíticamente las parábolas (basándose en ecuaciones), se suele afirmar erróneamente que los parámetros de la ecuación cambian la forma de la parábola, haciéndola más ancha o estrecha.
Un argumento geométrico informal es que al ser la directriz una recta infinita, al tomar cualquier punto y efectuar la construcción descrita arriba, se obtiene siempre la misma curva, salvo su escala, que depende de la distancia del punto a la directriz.
, y como la desigualdad es estricta, no hay otro punto de la parábola que toque a la recta
La curva dual de la parábola respecto a un círculo interior es una elipse.
La dual de la parábola respecto a un círculo exterior es una hipérbola.
Las aplicaciones prácticas son muchas: las antenas satelitales y radiotelescopios aprovechan el principio concentrando señales recibidas desde un emisor lejano en un receptor colocado en la posición del foco.
La concentración de la radiación solar en un punto, mediante un reflector parabólico tiene su aplicación en pequeñas cocinas solares y grandes centrales captadoras de energía solar.
Análogamente, una fuente emisora situada en el foco, enviará un haz de rayos paralelos al eje: diversas lámparas y faros tienen espejos con superficies parabólicas reflectantes para poder enviar haces de luz paralelos emanados de una fuente en posición focal.
Los rayos convergen o divergen si el emisor se desplaza de la posición focal.
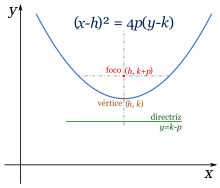
La ecuación de una parábola cuyo eje es vertical y su vértice es
Puede haber muchas parábolas que tengan un mismo vértice (variando el parámetro a) en la primera ecuación.
Sin embargo, dados dos puntos fijos, existe solamente una parábola que los tiene por vértice y foco, ya que la directriz queda automáticamente fija como la perpendicular a la línea que une el foco con el vértice y a esa misma distancia del último.
Cuando la parábola es horizontal «hacia la derecha», se obtiene una ecuación similar intercambiando los roles de x, y: La ecuación de una parábola con vértice en (0,0) y foco en (p,0) es
Finalmente, las ecuaciones cuando el vértice no está en el centro se obtienen mediante una traslación.
En el caso común de la parábola vertical hacia arriba se tiene La ecuación de una parábola con vértice en (h,k) y foco en (h,k + p) es
, mientras que para la parábola horizontal se intercambia x con y: La ecuación de una parábola con vértice en (h,k) y foco en (h + p,k) es
Mediante traslaciones y rotaciones es posible hallar un sistema de referencia en el que la ecuación anterior se exprese mediante una fórmula algebraica de la forma
La parábola se puede utilizar como trisectriz, es decir, permite realizar la trisección exacta de un ángulo arbitrario al ser utilizada como medio auxiliar de una construcción con regla y compás.
Esta trisección se remonta a René Descartes, quien la describió en su libro La Géométrie (1637).