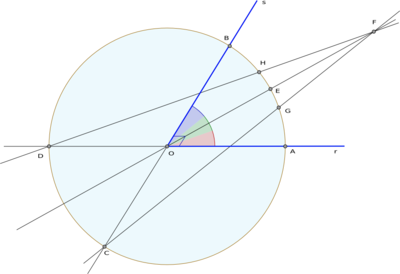
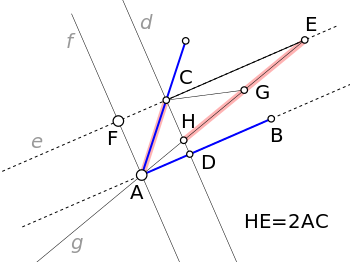
Trisección del ángulo

El problema es sencillo en algunos casos (por ejemplo, si el ángulo dado es recto o si en el barrido por la circunferencia total puede construirse un ángulo que sea la tercera parte del mismo), pero es imposible de resolver en general, como demostró Pierre Wantzel en su artículo Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compas, de 1837.La cuadratura del círculo también es imposible, como probó Carl Louis Ferdinand von Lindemann en 1882.Es posible trisecar un ángulo arbitrario utilizando herramientas distintas a la regla y el compás.Por ejemplo, el método neusis, también conocido por los antiguos griegos, implica el deslizamiento y la rotación simultáneos de una regla graduada, lo que no se puede lograr con las herramientas originales.Estas soluciones a menudo implican interpretaciones erróneas de las reglas o simplemente son incorrectas.Sin embargo, tres problemas específicos resultaron ser especialmente esquivos: trisecar un ángulo, duplicar un cubo y cuadrar un círculo.Debido a que p(t) tiene grado 3, si tiene solución en Q, entonces tiene una raíz racional.Por lo tanto, p(t) es irreducible sobre Q, y el polinomio mínimo para cos 20° es de grado 3.Nuevamente, denótese el conjunto de los números racionales por Q. Teorema: un ángulo de medida θ se puede trisecar si y solo si se puede reducir sobre la extensión del cuerpo Q(cos(θ)).Se han propuesto muchos métodos incorrectos para trisecar un ángulo en general.El matemático Underwood Dudley ha detallado algunos de estos intentos fallidos en su libro "The trisectors" (Los Trisectores).Dividiendo el numerador y el denominador del primer miembro de la expresión anterior, resulta:La trisección se puede aproximar mediante la repetición del método de la regla y el compás para bisecar un ángulo.[9]​ Un ángulo se puede trisecar con un dispositivo que es esencialmente una versión de cuatro brazos de un compás, con conexiones articuladas intermedias diseñadas para mantener iguales los tres ángulos entre los brazos adyacentes.[10]​ Este dispositivo fue estudiado por René Descartes en 1629, según consta en su correspondencia con Isaac Beeckman.La semejanza de los tres triángulos HAA', P'AA' y P'AB' demuestra que las rectas AP' y AA' dividen el ángulo dAh0 en tres ángulos de la misma medida.En 1932, Ludwig Bieberbach publicó en el "Journal für die reine und angewandte Mathematik" su obra "Zur Lehre von den kubischen Konstruktionen".[13]​ Según sus propias palabras (traducción libre): La siguiente descripción de la construcción (animación adyacente) contiene su continuación hasta la trisección completa del ángulo.En el siguiente paso se utiliza el llamado "medio de construcción adicional", que en el ejemplo ilustrado es el "Geodreieck".El triángulo se debe colocar sobre el dibujo de la siguiente manera: el vértice del ángulo recto determina el punto(de acuerdo con el ajuste del ángulo recto mencionado anteriormente como Rechtwinkelhaken).Hay ciertas curvas llamadas trisectrices que, si se dibujan en el plano usando otros métodos distintos de la regla y el compás, se pueden usar para trisecar ángulos arbitrarios.Ahora, los triángulos ABC y BCD son isósceles, por lo tanto (según el tercer principio), cada uno tiene dos ángulos iguales.Construcción: Dado cualquier ángulo CÂB (véase la figura adjunta), se considera una recta, ajustándola de forma que (véase método neusis): Demostración: La construcción cumple las siguientes condiciones: SeaTras devolver el cilindro a su posición original, los dos nuevos puntos generados se corresponden con la trisección del ángulo de partida.Un dispositivo trisector o "tomahawk" es una forma geométrica que consta de un semicírculo y dos segmentos ortogonales, de modo que la longitud del segmento más corto es igual al radio del círculo.Aunque el "tomahawk" se puede construir con regla y compás, generalmente no es posible colocarlo en la posición que resuelve el problema utilizando exclusivamente estos dos elementos.Un ecuación de tercer grado con coeficientes reales se puede resolver geométricamente con compás, regla y un trisector de ángulos si y solo si tiene tres raíces reales.[16]​: Thm.(es decir, son números primos de Pierpont mayores que 3).[16]​: Thm.