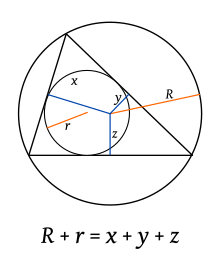Triángulo

En geometría plana, se llama triángulo, trígono o trigonoide al polígono de tres lados.

Los puntos comunes a cada par de lados se denominan vértices del triángulo.

Si está contenido en una superficie plana se denomina triángulo o trígono, un nombre menos común para este tipo de polígonos.

Tal como los vértices de un polígono, suelen ser denotados por letras latinas mayúsculas:

Un triángulo se nombra, entonces, como cualquier otro polígono, designando sucesivamente sus vértices, por ejemplo ABC.

Cada par de vértices determina un segmento, que se conoce como lado del triángulo.

Los lados del triángulo se denotan, como todos los segmentos, por sus extremos: AB, BC y AC.

Dos triángulos rectángulos son semejantes si cumplen con al menos uno de los criterios siguientes: Se consideran dos triángulos semejantes con lados paralelos y con circuncentro común ( centro de la circunferencia circunscrita).

Un punto es interior si está entre las intersecciones que determina un rayo con origen en el circuncentro con los lados homólogos.

En cambio, si el cuarto punto agregado es no coplanar y no alineado, se obtiene un tetraedro que es el poliedro más simple y está conformado por 4 caras triángulares.

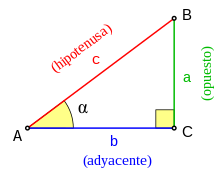
Para resolver triángulos (en general) se suele utilizar los teoremas del seno y del coseno, para el caso especial de triángulos rectángulos se utiliza generalmente el Teorema de Pitágoras.

Arcsin (arcoseno) puede ser usado para calcular un ángulo con la longitud del cateto opuesto y la de la hipotenusa.

Arccos (arcocoseno) puede ser usado para calcular un ángulo con la longitud del cateto adyacente y la de la hipotenusa.

Sin embargo, la notación de arcsin, arccos, etc., es estándar en matemáticas superiores donde las funciones trigonométricas son comúnmente elevadas a potencias, pues esto evita la confusión entre el inverso multiplicativo y la función inversa.

Dado un punto en el plano euclídeo, diremos que este es interior a un triángulo si al trazar una recta por él, dicho punto se halla entre los cortes con los lados del triángulo.

[15]​ Los tres lados de un triángulo constituyen su frontera y los puntos del plano que no están en el interior ni en la frontera están en el exterior del triángulo.

radios de las circunferencias exinscritas de un triángulo ABC; R y r radios de la circunfrencia circunscrita e inscrita en el mismo triángulo, respectivamente, entonces se cumple la ecuación que sigue: [27]​ Para cualquier triángulo, donde h = la menor altura, l = la menor bisectriz y S el área, se cumple lo siguiente Se nombra simediana a la recta (ceviana) que es simétrica a la mediana, siendo el eje de simetría la bisectriz con el mismo vértice.

de las circunferencias circunscrita e inscrita, respectivamente, del triángulo:[37]​ Usando un lado, llamado base, y la altura correspondiente, es decir, la distancia del vértice opuesto a la recta que el lado define, el área de un triángulo es igual al semiproducto de la base por su altura respectiva.

Conociendo la longitud de los tres lados a, b y c, se puede calcular el área para cualquier triángulo euclideo.

Conociendo la longitud de los tres lados a, b y c, se puede calcular el área para cualquier triángulo euclideo, (estas fórmulas no requieren precalcular el semiperímetro ni conocer la altura).

- S) = sen(S) e igualmente: Si un triángulo cualquiera (en el plano euclidiano ℝ²), tiene alguno de sus vértices (supongamos el A) ubicado en (0, 0) —el origen de las coordenadas cartesianas—, y las coordenadas de los otros dos vértices (supongamos B y C) vienen dadas por B = (xB, yB) y C = (xC, yC), entonces el área puede ser calculada como ½ del valor absoluto del determinate (reducido a los dos vértices arbitrarios B y C).

Para un triángulo genérico (en el espacio euclidiano ℝ³), cuyas coordenadas son { A = (xA, yA, zA), B = (xB, yB, zB) y C = (xC, yC, zC) }, entonces el área viene dada por la suma pitagórica de las áreas de las respectivas proyecciones sobre los tres planos principales (es decir x = 0, y = 0 y z = 0):

Sin embargo para ℝn, n > 3, uno de los vectores se usa como base, luego se obtiene el coseno del ángulo que forman los lados concurrentes en A, por medio del producto escalar de los vectores correspondiente a dichos lados.

Después el seno de tal ángulo, que propicia hallar la altura del triángulo.

[44]​ En estos espacios está definido el producto escalar ( interno) de vectores .

: [47]​[48]​ Ver, también, terna pitagórica En estas fórmulas, u y v son dos enteros positivos arbitrarios de distinta paridad tales que u > v y son primos entre sí.

Como el lector puede apreciar, aunque estas fórmulas fueron diseñadas para obtener ternas con lados enteros, al ser una identidad, también son válidas para lados reales, exceptuando el caso en que ambos catetos son iguales (que la hipotenusa sea diagonal de un cuadrado).

Pero en algunos casos, su escritura puede echar luz sobre cuestiones que de otra forma pasan inadvertidas.

Sin embargo, la fórmula utilizada para calcular el área hace pensar en la interpretación en favor de la primera solución.

[55]​ El escriba tomaba la mitad de la base del triángulo y calculaba el área del rectángulo formado por ese lado y la altura; es decir equivalente a la fórmula común utilizada en nuestros días: El hecho de que un triángulo de lados 3-4-5 es un triángulo rectángulo también era conocido por los antiguos egipcios y mesopotámicos.