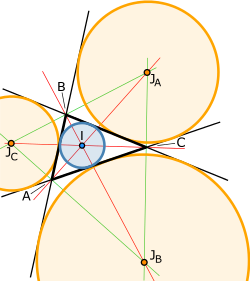
Circunferencia exinscrita

Al centro de la circunferencia exinscrita se le llama exincentro.

Las bisectrices interiores y exteriores (en rojo) se intersecan en cuatro puntos: uno es el centro del círculo inscrito (en pardo), y los demás son centros de los círculos exinscritos (en amarillo).

Estos últimos están "inscritos" en el sentido de que son tangentes simultáneamente a los tres lados, y se hallan al exterior del triángulo, de ahí su apelación.

Para demostrar que dos bisectrices exteriores de dos ángulos de un triángulo y la bisectriz interna del tercer ángulo concurren tomemos, por ejemplo, la bisectriz interior en A y las exteriores en B y C: Por lo anterior, el punto A' es equidistante de los tres lados (AB), (AC) y (BC).

[3]​ Todo triángulo posee tres exincentros, uno en el trapecio infinito exterior de cada lado.. Desde él, se puede trazar una circunferencia que es tangente a un lado y la prolongación de los otros dos.