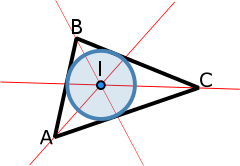
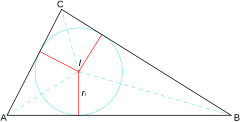
Incentro

El Incentro de un triángulo (marcado con la letra I en el gráfico) es el punto en el que se cortan las tres bisectrices de sus ángulos internos.Equidista de los tres lados, y por lo tanto, es el centro de la circunferencia inscrita en el triángulo, tangente a sus tres lados.Junto con el centroide (o baricentro) , circuncentro y ortocentro, es uno de los cuatro puntos notables del triángulo conocidos por los antiguos griegos, y el único que no se sitúa sobre la recta de Euler.Se pueden deducir las coordenadas cartesianas del incentro a partir de las coordenadas de los tres vértices del triángulo A, B y C. Si los vértices tienen por coordenadasLas coordenadas trilineales del incentro son La colección de centros del triángulo presenta estructura de grupo cuando se expresan sus coordenadas en el sistema trilineal respecto a la operación producto.son los ángulos de los tres vértices del triángulo.Denominando al incentro del triángulo ABC como I, las distancias desde el incentro a los vértices, de acuerdo con las longitudes de los lados, obedecen a la ecuación[4]​ Adicionalmente,[5]​ donde R y r son los radios de las circunferencias circunscrita e inscrita respectivamente.Conociendo el ángulo A y el radio r 2.Se reemplaza r y csc A/2 en la fórmula anterior (1).[7]​ La distancia entre el incentro y el centroide es menor que una tercera parte de la longitud de la mediana más larga del triángulo.[8]​ De acuerdo con el Teorema geométrico de Euler, la distancia entre el incentro I y el circuncentro O elevada al cuadrado, viene dada por[9]​[10]​ donde R y r son el circunradio y el inradio respectivamente; en consecuencia, el circunradio es al menos dos veces el inradio (siendo exactamente el doble únicamente en el caso del triángulo equilátero[11]​: p. 198 ).La distancia desde el incentro al centro N de la circunferencia de los nueve puntos es[10]​ La distancia al cuadrado entre el incentro y el ortocentro H es[12]​ Existen inecuaciones que afirman que: El incentro es el punto de Nagel del triángulo medial (el triángulo cuyos vértices son los puntos medios de los lados) y se halla situado en el interior de este triángulo.[13]​ El incentro se localiza en el interior de un disco cuyo diámetro une el centroide G y el ortocentro H (el disco ortocentroidal), pero no puede coincidir con el centro de los nueve puntos, cuya posición es fija a 1/4 a lo largo del diámetro (más cercano a G).El incentro generalmente no pertenece a la recta de Euler;[15]​ salvo para los triángulos isósceles,[16]​ en cuyo caso la recta de Euler coincide con el eje de simetría del triángulo y contiene todos sus centros.Denominando a la distancia desde el incentro a la recta de Euler d; a la longitud de la mayor mediana v; a la longitud del mayor lado del triángulo u; al circunradio R; a la longitud del segmento de la recta de Euler desde el ortocentro hasta el circuncentro e; y al semiperímetro s; se tienen las inecuaciones siguientes:[17]​ Cualquier recta que divida un triángulo en dos partes de igual área e igual perímetro (ambas condiciones se dan simultáneamente), pasa por su incentro.Puede haber una, dos o tres de estas líneas para cualquier triángulo dado.[18]​ Sea X un punto de la bisectriz del ángulo A.Entonces, cuando X = I (el incentro) se maximiza o minimiza el cociente