Coordenadas baricéntricas (n-simplex)
Las coordenadas baricéntricas permiten parametrizar mediante n+1 números reales en el intervalo [0,1] el interior de un n-simplex.
En realidad, de las n+1 coordenadas baricéntricas solo n son independientes, ya que la suma de todas es igual a uno.
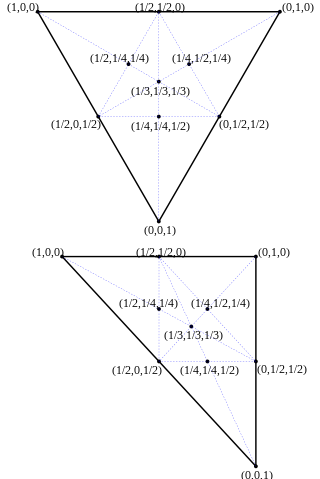
Como ejemplo introductorio se considera un triángulo en el plano euclídeo
puede ser representado por tres coordenadas baricéntricas
Donde la relación entre las coordenadas cartesianas y las baricéntricas viene dada por:
Dicha web cuenta con miles de centros con coordenadas baricéntricas y trilineales.
Normalmente solo aparece la 1ª (alfa), pero al ser homogéneas se pueden deducir las otras 2 permutando las letras de la 1ª, por ejemplo, el punto P =
β = b ( c − a )
γ = c ( a − b )
{\displaystyle P=(a(b-c):b(c-a):c(a-b))}
Es decir, solo hay 3 letras: a,b,c ya que el triángulo solo tiene 3 lados, y cada letra corresponde a la longitud de un lado.
Si empieza en la a, la siguiente es la b, y la última la c. Si comienza en la b, la siguiente es la c y la siguiente, como no hay d, recomienza en la a.
Si comienza en la c, al ser una triada cíclica, la siguiente es la a y después la b.
Si el punto o centro Kimberling viniera en coordenadas trilineales, basta convertirlas a baricéntricas multiplicando cada una por una letra distinta: a,b,c.
El triángulo estará formado por todos los puntos del conjunto T:
El lado a (opuesto al vértice A) será el conjunto de puntos: (left)
y análogamente los lados b y c por lo que la frontera del triángulo estará formada por los puntos tales que alguna de sus coordenadas baricéntricas sea cero.
Y los vértices satisfacen que una de sus coordenadas baricéntricas es uno y las otras son nulas.
La construcción anterior puede ampliarse a un tetraedro, no necesariamente regular, en el espacio euclídeo
Si los vértices del tetraedro en cuestión son
puede ser representado por cuatro coordenadas baricéntricas
{\displaystyle (t_{A},t_{B},t_{C},t_{D})}
{\displaystyle t_{A}+t_{B}+t_{C}+t_{D}=1\,\qquad 0\leq t_{X}\leq 1}
Donde la relación entre las coordenadas cartesianas y las baricéntricas viene dada por:
{\displaystyle {\begin{cases}x=t_{A}x_{A}+t_{B}x_{B}+t_{C}x_{C}+t_{D}x_{D}\\y=t_{A}y_{A}+t_{B}y_{B}+t_{C}y_{C}+t_{D}y_{D}\\z=t_{A}z_{A}+t_{B}z_{B}+t_{C}z_{C}+t_{D}z_{D}\end{cases}}}
Dado un punto P si ninguna de las coordenadas baricéntricas es cero
el punto será un interior, si solo una de ellas es cero será un punto interior a una de las caras del tetraedro, si dos y solo dos de las coordenadas baricéntricas son cero el punto será el interior de una arista y si tres de las coordenadas baricéntricas son cero (y por tanto la otra igual a 1) el punto será un vértice.
Dado un n-simplex (o simplex) en el espacio euclídeo
, se pueden definir las coordenadas baricéntricas generalizadas.
Donde la relación entre las coordenadas cartesianas y las baricéntricas viene dada por: