

Las matemáticas y el arte están relacionadas de diversas maneras. Las matemáticas en sí mismas han sido descritas como un arte motivado por la belleza . Las matemáticas pueden percibirse en artes como la música , la danza , la pintura , la arquitectura , la escultura y los textiles . Sin embargo, este artículo se centra en las matemáticas en las artes visuales.
Las matemáticas y el arte tienen una larga relación histórica. Los artistas han utilizado las matemáticas desde el siglo IV a. C., cuando el escultor griego Policleto escribió su Canon , prescribiendo proporciones que se supone que se basaban en la razón 1: √ 2 para el desnudo masculino ideal. Se han hecho afirmaciones populares persistentes sobre el uso de la proporción áurea en el arte y la arquitectura antiguos, sin evidencia confiable. En el Renacimiento italiano , Luca Pacioli escribió el influyente tratado De divina percentagee (1509), ilustrado con xilografías de Leonardo da Vinci , sobre el uso de la proporción áurea en el arte. Otro pintor italiano, Piero della Francesca , desarrolló las ideas de Euclides sobre la perspectiva en tratados como De Prospectiva Pingendi y en sus pinturas. El grabador Alberto Durero hizo muchas referencias a las matemáticas en su obra Melencolia I. En la época moderna, el artista gráfico M. C. Escher hizo un uso intensivo de la teselación y la geometría hiperbólica , con la ayuda del matemático HSM Coxeter , mientras que el movimiento De Stijl liderado por Theo van Doesburg y Piet Mondrian adoptó explícitamente las formas geométricas. Las matemáticas han inspirado artes textiles como el acolchado , el tejido , el punto de cruz , el crochet , el bordado , el tejido , la confección de alfombras turcas y de otros tipos , así como los kilims . En el arte islámico , las simetrías son evidentes en formas tan variadas como el girih persa y el mosaico zellige marroquí , las pantallas de piedra perforada jali mogol y las bóvedas de muqarnas generalizadas .
Las matemáticas han influido directamente en el arte con herramientas conceptuales como la perspectiva lineal , el análisis de la simetría y objetos matemáticos como los poliedros y la cinta de Möbius . Magnus Wenninger crea poliedros estrellados coloridos , originalmente como modelos para la enseñanza. Los conceptos matemáticos como la recursión y la paradoja lógica se pueden ver en las pinturas de René Magritte y en los grabados de MC Escher. El arte informático a menudo hace uso de fractales , incluido el conjunto de Mandelbrot , y a veces explora otros objetos matemáticos como los autómatas celulares . De manera controvertida, el artista David Hockney ha argumentado que los artistas desde el Renacimiento en adelante hicieron uso de la cámara lúcida para dibujar representaciones precisas de escenas; el arquitecto Philip Steadman argumentó de manera similar que Vermeer usó la cámara oscura en sus pinturas distintivamente observadas.
Otras relaciones incluyen el análisis algorítmico de obras de arte mediante espectroscopia de fluorescencia de rayos X , el hallazgo de que los batiks tradicionales de diferentes regiones de Java tienen dimensiones fractales distintas y estímulos a la investigación matemática, especialmente la teoría de la perspectiva de Filippo Brunelleschi , que eventualmente condujo a la geometría proyectiva de Girard Desargues . Una visión persistente, basada en última instancia en la noción pitagórica de armonía en la música, sostiene que todo fue organizado por Número, que Dios es el geómetra del mundo y que, por lo tanto, la geometría del mundo es sagrada .

Policleto el Viejo (c. 450–420 a. C.) fue un escultor griego de la escuela de Argos , contemporáneo de Fidias . Sus obras y estatuas consistían principalmente en bronce y representaban a atletas. Según el filósofo y matemático Jenócrates , Policleto está clasificado como uno de los escultores más importantes de la antigüedad clásica por su trabajo en el Doríforo y la estatua de Hera en el Hereo de Argos . [3] Aunque sus esculturas pueden no ser tan famosas como las de Fidias, son muy admiradas. En su Canon , un tratado que escribió diseñado para documentar las proporciones corporales "perfectas" del desnudo masculino, Policleto nos da un enfoque matemático para esculpir el cuerpo humano. [3]
El canon en sí se ha perdido, pero se conjetura que Policleto utilizó una secuencia de proporciones donde cada longitud es la de la diagonal de un cuadrado dibujado sobre su predecesor, 1: √ 2 (aproximadamente 1:1.4142). [4]
La influencia del Canon de Policleto es inmensa en la escultura clásica griega , romana y renacentista , y muchos escultores siguieron la prescripción de Policleto. Si bien no sobrevive ninguna de las obras originales de Policleto, las copias romanas demuestran su ideal de perfección física y precisión matemática. Algunos estudiosos sostienen que el pensamiento pitagórico influyó en el Canon de Policleto. [5] El Canon aplica los conceptos matemáticos básicos de la geometría griega, como la razón, la proporción y la simetría (del griego "proporciones armoniosas") y los convierte en un sistema capaz de describir la forma humana a través de una serie de progresiones geométricas continuas . [4]

En la época clásica, en lugar de hacer que las figuras distantes fueran más pequeñas con la perspectiva lineal , los pintores dimensionaban los objetos y las figuras según su importancia temática. En la Edad Media, algunos artistas usaban la perspectiva inversa para dar un énfasis especial. El matemático musulmán Alhazen (Ibn al-Haytham) describió una teoría de la óptica en su Libro de Óptica en 1021, pero nunca la aplicó al arte. [6] El Renacimiento vio un renacimiento de la cultura y las ideas clásicas griegas y romanas, entre ellas el estudio de las matemáticas para comprender la naturaleza y las artes . Dos motivos principales impulsaron a los artistas de finales de la Edad Media y el Renacimiento hacia las matemáticas. En primer lugar, los pintores necesitaban descubrir cómo representar escenas tridimensionales en un lienzo bidimensional. En segundo lugar, tanto los filósofos como los artistas estaban convencidos de que las matemáticas eran la verdadera esencia del mundo físico y que todo el universo, incluidas las artes, podían explicarse en términos geométricos. [7]
Los rudimentos de la perspectiva llegaron con Giotto (1266/7 – 1337), quien intentó dibujar en perspectiva utilizando un método algebraico para determinar la ubicación de las líneas distantes. En 1415, el arquitecto italiano Filippo Brunelleschi y su amigo Leon Battista Alberti demostraron el método geométrico de aplicación de la perspectiva en Florencia, utilizando triángulos similares según lo formulado por Euclides, para encontrar la altura aparente de los objetos distantes. [8] [9] Las propias pinturas en perspectiva de Brunelleschi se han perdido, pero la pintura de la Santísima Trinidad de Masaccio muestra sus principios en acción. [6] [10] [11]
_01.jpg/440px-San_Romano_Battle_(Paolo_Uccello,_London)_01.jpg)
El pintor italiano Paolo Uccello (1397-1475) estaba fascinado por la perspectiva, como se muestra en sus pinturas de La batalla de San Romano (c. 1435-1460): las lanzas rotas se ubican convenientemente a lo largo de las líneas de perspectiva. [12] [13]
El pintor Piero della Francesca (c. 1415-1492) ejemplificó este nuevo cambio en el pensamiento renacentista italiano. Fue un matemático y geómetra experto , que escribió libros sobre geometría de sólidos y perspectiva , incluidos De prospectiva pingendi (Sobre la perspectiva para la pintura) , Trattato d'Abaco (Tratado del ábaco) y De quinque corporibus regularibus (Sobre los cinco sólidos regulares) . [14] [15] [16] El historiador Vasari en sus Vidas de los pintores llama a Piero el "mayor geómetra de su tiempo, o quizás de cualquier tiempo". [17] El interés de Piero por la perspectiva se puede ver en sus pinturas, incluido el Políptico de Perugia , [18] el retablo de San Agostino y La flagelación de Cristo . Su trabajo sobre geometría influyó en matemáticos y artistas posteriores, incluido Luca Pacioli en su De divina proporción y Leonardo da Vinci . Piero estudió matemáticas clásicas y las obras de Arquímedes . [19] Le enseñaron aritmética comercial en "escuelas de ábaco"; sus escritos tienen el formato de los libros de texto de las escuelas de ábaco, [20] tal vez incluyendo el Liber Abaci de Leonardo Pisano ( Fibonacci ) de 1202. La perspectiva lineal estaba recién introduciéndose en el mundo artístico. Alberti explicó en su De pictura de 1435 : "los rayos de luz viajan en línea recta desde puntos en la escena observada hasta el ojo, formando una especie de pirámide con el ojo como vértice". Una pintura construida con perspectiva lineal es una sección transversal de esa pirámide. [21]
En De Prospectiva Pingendi , Piero transforma sus observaciones empíricas sobre la forma en que los aspectos de una figura cambian con el punto de vista en pruebas matemáticas. Su tratado comienza en la línea de Euclides: define el punto como "la cosa más pequeña que es posible que el ojo comprenda". [a] [7] Utiliza la lógica deductiva para llevar al lector a la representación en perspectiva de un cuerpo tridimensional. [22]
El artista David Hockney argumentó en su libro Secret Knowledge: Rediscovering the Lost Techniques of the Old Masters que los artistas comenzaron a usar una cámara lúcida a partir de la década de 1420, lo que resultó en un cambio repentino en la precisión y el realismo, y que esta práctica fue continuada por artistas importantes como Ingres , Van Eyck y Caravaggio . [23] Los críticos no están de acuerdo sobre si Hockney estaba en lo cierto. [24] [25] De manera similar, el arquitecto Philip Steadman argumentó controvertidamente [26] que Vermeer había usado un dispositivo diferente, la cámara oscura , para ayudarlo a crear sus pinturas distintivamente observadas. [27]
En 1509, Luca Pacioli (c. 1447-1517) publicó De divina percentagee sobre la proporción matemática y artística , incluso en el rostro humano. Leonardo da Vinci (1452-1519) ilustró el texto con xilografías de sólidos regulares mientras estudiaba con Pacioli en la década de 1490. Los dibujos de Leonardo son probablemente las primeras ilustraciones de sólidos esqueletizados. [28] Estos, como el rombicuboctaedro , fueron de los primeros en ser dibujados para demostrar la perspectiva al superponerse uno sobre el otro. La obra analiza la perspectiva en las obras de Piero della Francesca , Melozzo da Forlì y Marco Palmezzano . [29] Leonardo estudió la Summa de Pacioli , de la que copió tablas de proporciones. [30] En Mona Lisa y La última cena , la obra de Leonardo incorporó la perspectiva lineal con un punto de fuga para proporcionar una profundidad aparente. [31] La Última Cena está construida en una proporción estricta de 12:6:4:3, al igual que La Escuela de Atenas de Rafael , que incluye a Pitágoras con una tablilla de proporciones ideales, sagrada para los pitagóricos. [32] [33] En El Hombre de Vitruvio , Leonardo expresó las ideas del arquitecto romano Vitruvio , mostrando de manera innovadora la figura masculina dos veces y centrándola tanto en un círculo como en un cuadrado. [34]
Ya en el siglo XV, la perspectiva curvilínea se abrió camino en las pinturas de artistas interesados en las distorsiones de la imagen. El Retrato de Arnolfini de Jan van Eyck de 1434 contiene un espejo convexo con reflejos de las personas en la escena, [35] mientras que el Autorretrato en un espejo convexo de Parmigianino , c. 1523-1524, muestra el rostro del artista en gran parte sin distorsión en el centro, con un fondo fuertemente curvado y la mano del artista alrededor del borde. [36]
El espacio tridimensional puede representarse de manera convincente en el arte, como en el dibujo técnico , por otros medios además de la perspectiva. Las proyecciones oblicuas , incluida la perspectiva caballera (utilizada por los artistas militares franceses para representar fortificaciones en el siglo XVIII), fueron utilizadas de manera continua y ubicua por los artistas chinos desde el siglo I o II hasta el siglo XVIII. Los chinos adquirieron la técnica de la India, que la adquirió de la Antigua Roma. La proyección oblicua se ve en el arte japonés, como en las pinturas Ukiyo-e de Torii Kiyonaga (1752-1815). [37]
La proporción áurea (aproximadamente igual a 1,618) era conocida por Euclides . [38] Se ha afirmado persistentemente [39] [40] [41] [42] en los tiempos modernos que la proporción áurea se utilizó en el arte y la arquitectura por los antiguos en Egipto, Grecia y otros lugares, sin evidencia confiable. [43] La afirmación puede derivar de la confusión con "proporción áurea", que para los antiguos griegos significaba "evitar el exceso en cualquier dirección", no una proporción. [43] Los piramidólogos desde el siglo XIX han argumentado sobre bases matemáticas dudosas para la proporción áurea en el diseño de pirámides. [b] Se ha afirmado que el Partenón , un templo del siglo V a. C. en Atenas, utilizó la proporción áurea en su fachada y planta, [47] [48] [49] pero estas afirmaciones también están refutadas por la medición. [43] También se ha afirmado que la Gran Mezquita de Kairouan en Túnez utilizó la proporción áurea en su diseño, [50] pero la proporción no aparece en las partes originales de la mezquita. [51] El historiador de arquitectura Frederik Macody Lund argumentó en 1919 que la Catedral de Chartres (siglo XII), Notre-Dame de Laon (1157-1205) y Notre Dame de París (1160) están diseñadas según la proporción áurea, [52] dibujando líneas reguladoras para respaldar su argumento. Otros académicos sostienen que hasta la obra de Pacioli en 1509, la proporción áurea era desconocida para los artistas y arquitectos. [53] Por ejemplo, la altura y el ancho del frente de Notre-Dame de Laon tienen la proporción 8/5 o 1,6, no 1,618. Tales proporciones de Fibonacci rápidamente se vuelven difíciles de distinguir de la proporción áurea. [54] Después de Pacioli, la proporción áurea se percibe con mayor claridad en obras de arte como la Mona Lisa de Leonardo . [55]
Otra razón, el único otro número mórfico, [56] fue denominado número plástico [c] en 1928 por el arquitecto holandés Hans van der Laan (originalmente llamado le nombre radiant en francés). [57] Su valor es la solución de la ecuación cúbica
un número irracional que es aproximadamente 1,325. Según el arquitecto Richard Padovan , este tiene proporciones características .3/4 y 1/7, que rigen los límites de la percepción humana al relacionar un tamaño físico con otro. Van der Laan utilizó estas proporciones al diseñar la iglesia de la abadía de San Benedicto en los Países Bajos en 1967. [57]

Las simetrías planas se han explotado durante milenios en obras de arte como alfombras , celosías, textiles y azulejos. [59] [60] [61] [62]
Muchas alfombras tradicionales, ya sean alfombras de pelo o kilims de tejido plano , se dividen en un campo central y un borde que enmarca; ambos pueden tener simetrías, aunque en las alfombras tejidas a mano estas a menudo se rompen ligeramente por pequeños detalles, variaciones de patrón y cambios de color introducidos por el tejedor. [59] En los kilims de Anatolia , los motivos utilizados suelen ser simétricos. El diseño general también suele estar presente, con disposiciones como rayas, rayas alternadas con filas de motivos y conjuntos compactos de motivos aproximadamente hexagonales. El campo se presenta comúnmente como un papel tapiz con un grupo de papel tapiz como pmm, mientras que el borde puede presentarse como un friso del grupo de frisos pm11, pmm2 o pma2. Los kilims turcos y de Asia Central a menudo tienen tres o más bordes en diferentes grupos de frisos. Los tejedores ciertamente tenían la intención de la simetría, sin un conocimiento explícito de sus matemáticas. [59] El matemático y teórico de la arquitectura Nikos Salingaros sugiere que la "poderosa presencia" [58] (efecto estético) de una "gran alfombra" [58] como las mejores alfombras de dos medallones de Konya del siglo XVII se crea mediante técnicas matemáticas relacionadas con las teorías del arquitecto Christopher Alexander . Estas técnicas incluyen hacer que los opuestos se acoplen; oponer valores de color; diferenciar áreas geométricamente, ya sea mediante el uso de formas complementarias o equilibrando la direccionalidad de los ángulos agudos; proporcionar complejidad a pequeña escala (desde el nivel de nudo hacia arriba) y simetría tanto a pequeña como a gran escala; repetir elementos en una jerarquía de diferentes escalas (con una relación de aproximadamente 2,7 de cada nivel al siguiente). Salingaros sostiene que "todas las alfombras exitosas satisfacen al menos nueve de las diez reglas anteriores", y sugiere que podría ser posible crear una métrica a partir de estas reglas. [58]
En la India, en el arte jali se encuentran elaboradas celosías talladas en mármol para adornar tumbas y palacios. [60] Las celosías chinas, siempre con cierta simetría, existen en 14 de los 17 grupos de papel pintado; a menudo tienen simetría especular, de doble espejo o rotacional. Algunas tienen un medallón central y otras tienen un borde en un grupo de frisos. [63] Daniel S. Dye ha analizado matemáticamente muchas celosías chinas; identifica a Sichuan como el centro de la artesanía. [64]
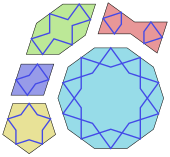
Las simetrías son prominentes en las artes textiles , incluyendo el acolchado , [61] el tejido , [65] el punto de cruz , el crochet , [66] el bordado [67] [68] y el tejido , [69] donde pueden ser puramente decorativas o pueden ser marcas de estatus. [70] La simetría rotacional se encuentra en estructuras circulares como cúpulas ; estas a veces están decoradas elaboradamente con patrones simétricos por dentro y por fuera, como en la Mezquita Sheikh Lotfollah de 1619 en Isfahán . [71] Los artículos de bordado y encaje como manteles y manteles individuales, hechos con bobinas o con frivolité , pueden tener una amplia variedad de simetrías reflexivas y rotacionales que se están explorando matemáticamente. [72]
El arte islámico explota las simetrías en muchas de sus formas artísticas, en particular en los mosaicos girih . Estos se forman utilizando un conjunto de cinco formas de mosaico, a saber, un decágono regular, un hexágono alargado, una pajarita, un rombo y un pentágono regular. Todos los lados de estos mosaicos tienen la misma longitud; y todos sus ángulos son múltiplos de 36° (π/5 radianes ), ofreciendo simetrías quíntuples y décuples. Los mosaicos están decorados con líneas de correas (girih), generalmente más visibles que los límites de los mosaicos. En 2007, los físicos Peter Lu y Paul Steinhardt argumentaron que el girih se parecía a los mosaicos cuasicristalinos de Penrose . [73] El elaborado mosaico geométrico zellige es un elemento distintivo en la arquitectura marroquí . [62] Las bóvedas de muqarnas son tridimensionales, pero fueron diseñadas en dos dimensiones con dibujos de celdas geométricas. [74]
Los sólidos platónicos y otros poliedros son un tema recurrente en el arte occidental. Se encuentran, por ejemplo, en un mosaico de mármol que presenta el pequeño dodecaedro estrellado , atribuido a Paolo Uccello, en el piso de la Basílica de San Marcos en Venecia; [12] en los diagramas de poliedros regulares de Leonardo da Vinci dibujados como ilustraciones para el libro de Luca Pacioli de 1509 La divina proporción ; [12] como un rombicuboctaedro de vidrio en el retrato de Pacioli de Jacopo de Barbari, pintado en 1495; [12] en el poliedro truncado (y varios otros objetos matemáticos) en el grabado Melencolia I de Alberto Durero ; [12] y en la pintura de Salvador Dalí La última cena en la que Cristo y sus discípulos están representados dentro de un dodecaedro gigante . [75]
Alberto Durero (1471-1528) fue un grabador renacentista alemán que hizo importantes contribuciones a la literatura poliédrica en su libro de 1525, Underweysung der Messung (Educación sobre la medición) , destinado a enseñar los temas de perspectiva lineal , geometría en arquitectura , sólidos platónicos y polígonos regulares . Durero probablemente estuvo influenciado por las obras de Luca Pacioli y Piero della Francesca durante sus viajes a Italia . [76] Si bien los ejemplos de perspectiva en Underweysung der Messung están subdesarrollados y contienen imprecisiones, hay una discusión detallada de los poliedros. Durero también es el primero en introducir en el texto la idea de redes poliédricas , poliedros desplegados para quedar planos para imprimir. [77] Durero publicó otro libro influyente sobre las proporciones humanas llamado Vier Bücher von Menschlicher Proportion (Cuatro libros sobre la proporción humana) en 1528. [78]
El conocido grabado de Durero Melencolia I representa a un pensador frustrado sentado junto a un trapezoedro triangular truncado y un cuadrado mágico . [1] Estos dos objetos, y el grabado en su conjunto, han sido objeto de una interpretación más moderna que el contenido de casi cualquier otro grabado, [1] [79] [80] incluido un libro de dos volúmenes de Peter-Klaus Schuster, [81] y una discusión influyente en la monografía de Durero de Erwin Panofsky . [1] [82]
La pintura Corpus Hypercubus de Salvador Dalí de 1954 representa de manera única la cruz de Cristo como una red tridimensional desplegada para un hipercubo , también conocido como teseracto : el despliegue de un teseracto en estos ocho cubos es análogo a desplegar los lados de un cubo en una forma de cruz de seis cuadrados, que aquí representa la perspectiva divina con un poliedro regular de cuatro dimensiones. [83] [84] La pintura muestra la figura de Cristo frente al teseracto; normalmente se lo mostraría fijado con clavos a la cruz, pero no hay clavos en la pintura. En cambio, hay cuatro pequeños cubos frente a su cuerpo, en las esquinas del cubo de teseracto más delantero de los ocho. El matemático Thomas Banchoff afirma que Dalí estaba intentando ir más allá del mundo tridimensional, mientras que el poeta y crítico de arte Kelly Grovier dice que "la pintura parece haber roto el vínculo entre la espiritualidad de la salvación de Cristo y la materialidad de las fuerzas geométricas y físicas. Parece tender un puente sobre la división que muchos sienten que separa la ciencia de la religión". [85]

Los diseños tradicionales indonesios de batik con cera resistente sobre tela combinan motivos figurativos (como elementos florales y vegetales) con elementos abstractos y algo caóticos, incluida la imprecisión en la aplicación de la cera resistente y la variación aleatoria introducida por el agrietamiento de la cera. Los diseños de batik tienen una dimensión fractal entre 1 y 2, que varía en diferentes estilos regionales. Por ejemplo, el batik de Cirebon tiene una dimensión fractal de 1,1; los batik de Yogyakarta y Surakarta (Solo) en Java Central tienen una dimensión fractal de 1,2 a 1,5; y los batik de Lasem en la costa norte de Java y de Tasikmalaya en Java Occidental tienen una dimensión fractal entre 1,5 y 1,7. [86]
Las obras de pintura por goteo del artista moderno Jackson Pollock son igualmente distintivas en su dimensión fractal. Su Número 14 de 1948 tiene una dimensión similar a la de una costa de 1,45, mientras que sus pinturas posteriores tuvieron dimensiones fractales cada vez más altas y, en consecuencia, patrones más elaborados. Una de sus últimas obras, Blue Poles , tardó seis meses en crearse y tiene una dimensión fractal de 1,72. [87]
El astrónomo Galileo Galilei escribió en su Il Saggiatore que "[El universo] está escrito en el lenguaje de las matemáticas , y sus caracteres son triángulos, círculos y otras figuras geométricas". [88] Los artistas que se esfuerzan y buscan estudiar la naturaleza deben primero, en opinión de Galileo, comprender completamente las matemáticas. Los matemáticos, por el contrario, han buscado interpretar y analizar el arte a través de la lente de la geometría y la racionalidad. El matemático Felipe Cucker sugiere que las matemáticas, y especialmente la geometría, son una fuente de reglas para la "creación artística impulsada por reglas", aunque no la única. [89] A continuación se describen algunas de las muchas vertientes de la compleja relación resultante [90] .

El matemático Jerry P. King describe las matemáticas como un arte, afirmando que "las claves de las matemáticas son la belleza y la elegancia y no la monotonía y el tecnicismo", y que la belleza es la fuerza motivadora de la investigación matemática. [91] King cita el ensayo de 1940 del matemático GH Hardy A Mathematician's Apology . En él, Hardy analiza por qué considera dos teoremas de la época clásica como de primera categoría, a saber, la prueba de Euclides de que hay infinitos números primos y la prueba de que la raíz cuadrada de 2 es irracional . King evalúa este último en relación con los criterios de Hardy para la elegancia matemática : " seriedad, profundidad, generalidad, imprevisibilidad, inevitabilidad y economía " (cursiva de King), y describe la prueba como "estéticamente agradable". [92] El matemático húngaro Paul Erdős coincidía en que las matemáticas poseían belleza, pero consideraba que las razones estaban más allá de toda explicación: “¿Por qué son bellos los números? Es como preguntar por qué es bella la Novena Sinfonía de Beethoven . Si no ves por qué, nadie te lo puede decir. Yo sé que los números son bellos”. [93]
Las matemáticas se pueden discernir en muchas de las artes, como la música , la danza , [94] la pintura , la arquitectura y la escultura . Cada una de estas está ricamente asociada con las matemáticas. [95] Entre las conexiones con las artes visuales, las matemáticas pueden proporcionar herramientas para los artistas, como las reglas de la perspectiva lineal descritas por Brook Taylor y Johann Lambert , o los métodos de geometría descriptiva , ahora aplicados en el modelado de sólidos por software, que se remontan a Alberto Durero y Gaspard Monge . [96] Los artistas, desde Luca Pacioli en la Edad Media hasta Leonardo da Vinci y Alberto Durero en el Renacimiento, han hecho uso y desarrollado ideas matemáticas en la búsqueda de su trabajo artístico. [95] [97] El uso de la perspectiva comenzó, a pesar de algunos usos embrionarios en la arquitectura de la Antigua Grecia, con pintores italianos como Giotto en el siglo XIII; Las reglas como el punto de fuga fueron formuladas por primera vez por Brunelleschi alrededor de 1413, [6] su teoría influyó en Leonardo y Durero. El trabajo de Isaac Newton sobre el espectro óptico influyó en la Teoría de los colores de Goethe y, a su vez, en artistas como Philipp Otto Runge , JMW Turner , [98] los prerrafaelitas y Wassily Kandinsky . [99] [100] Los artistas también pueden optar por analizar la simetría de una escena. [101] Las herramientas pueden ser aplicadas por matemáticos que están explorando el arte, o artistas inspirados por las matemáticas, como MC Escher (inspirado por HSM Coxeter ) y el arquitecto Frank Gehry , quien argumentó de manera más tenue que el diseño asistido por computadora le permitió expresarse de una manera completamente nueva. [102]

El artista Richard Wright sostiene que los objetos matemáticos que se pueden construir pueden verse como "procesos para simular fenómenos" o como obras de " arte informático ". Considera la naturaleza del pensamiento matemático, observando que los fractales eran conocidos por los matemáticos durante un siglo antes de que fueran reconocidos como tales. Wright concluye afirmando que es apropiado someter los objetos matemáticos a cualquier método utilizado para "llegar a un acuerdo con los artefactos culturales como el arte, la tensión entre objetividad y subjetividad, sus significados metafóricos y el carácter de los sistemas de representación". Da como ejemplos una imagen del conjunto de Mandelbrot , una imagen generada por un algoritmo de autómata celular y una imagen renderizada por computadora , y analiza, con referencia a la prueba de Turing , si los productos algorítmicos pueden ser arte. [103] Math and Art: An Introduction to Visual Mathematics de Sasho Kalajdzievski adopta un enfoque similar, analizando temas de matemáticas adecuadamente visuales como mosaicos, fractales y geometría hiperbólica. [104]
Algunas de las primeras obras de arte por ordenador fueron creadas por "Drawing Machine 1" de Desmond Paul Henry , una máquina analógica basada en una computadora con mira de bombardeo y exhibida en 1962. [105] [106] La máquina era capaz de crear dibujos lineales complejos, abstractos, asimétricos, curvilíneos, pero repetitivos. [105] [107] Más recientemente, Hamid Naderi Yeganeh ha creado formas que sugieren objetos del mundo real, como peces y pájaros, utilizando fórmulas que se varían sucesivamente para dibujar familias de curvas o líneas en ángulo. [108] [109] [110] Artistas como Mikael Hvidtfeldt Christensen crean obras de arte generativo o algorítmico escribiendo scripts para un sistema de software como Structure Synth : el artista dirige efectivamente el sistema para aplicar una combinación deseada de operaciones matemáticas a un conjunto de datos elegido. [111] [112]

La Ciencia y la hipótesis del matemático y físico teórico Henri Poincaré fue ampliamente leída por los cubistas , incluidos Pablo Picasso y Jean Metzinger . [114] [115] Al estar completamente familiarizado con el trabajo de Bernhard Riemann sobre geometría no euclidiana, Poincaré era más que consciente de que la geometría euclidiana es solo una de las muchas configuraciones geométricas posibles, en lugar de una verdad objetiva absoluta. La posible existencia de una cuarta dimensión inspiró a los artistas a cuestionar la perspectiva clásica del renacimiento : la geometría no euclidiana se convirtió en una alternativa válida. [116] [117] [118] El concepto de que la pintura podía expresarse matemáticamente, en color y forma, contribuyó al cubismo, el movimiento artístico que condujo al arte abstracto . [119] Metzinger, en 1910, escribió que: "[Picasso] presenta una perspectiva libre y móvil, de la que ese ingenioso matemático Maurice Princet ha deducido toda una geometría". [120] Más tarde, Metzinger escribió en sus memorias:
Maurice Princet se unió a nosotros a menudo... fue como artista que conceptualizó las matemáticas, como esteta que invocó los continuos n -dimensionales. Le encantaba despertar el interés de los artistas por las nuevas visiones del espacio que habían abierto Schlegel y algunos otros. Y lo logró. [121]
El impulso de hacer modelos didácticos o de investigación de formas matemáticas crea naturalmente objetos que tienen simetrías y formas sorprendentes o agradables. Algunas de ellas han inspirado a artistas como los dadaístas Man Ray , [122] Marcel Duchamp [123] y Max Ernst , [124] [125] y, siguiendo a Man Ray, Hiroshi Sugimoto . [126]

Man Ray fotografió algunos de los modelos matemáticos del Instituto Henri Poincaré de París, entre ellos el Objet mathematique (Objeto matemático). Observó que representaba superficies de Enneper con curvatura negativa constante , derivadas de la pseudoesfera . Esta base matemática fue importante para él, ya que le permitió negar que el objeto fuera "abstracto", afirmando en cambio que era tan real como el urinario que Duchamp convirtió en una obra de arte. Man Ray admitió que la fórmula del objeto [superficie de Enneper] "no significaba nada para mí, pero las formas en sí mismas eran tan variadas y auténticas como cualquier otra en la naturaleza". Utilizó sus fotografías de los modelos matemáticos como figuras en su serie que hizo sobre las obras de Shakespeare , como su pintura de 1934 Antonio y Cleopatra . [127] El reportero de arte Jonathan Keats, escribiendo en ForbesLife , sostiene que Man Ray fotografió "los paraboloides elípticos y los puntos cónicos con la misma luz sensual que sus imágenes de Kiki de Montparnasse ", y "reutiliza ingeniosamente los fríos cálculos de las matemáticas para revelar la topología del deseo". [128] Escultores del siglo XX como Henry Moore , Barbara Hepworth y Naum Gabo se inspiraron en modelos matemáticos. [129] Moore escribió sobre su Madre e hijo con cuerdas de 1938 : "Sin duda, la fuente de mis figuras con cuerdas fue el Museo de la Ciencia ... Me fascinaron los modelos matemáticos que vi allí... No fue el estudio científico de estos modelos sino la capacidad de mirar a través de las cuerdas como con una jaula de pájaros y ver una forma dentro de otra lo que me emocionó". [130]

Los artistas Theo van Doesburg y Piet Mondrian fundaron el movimiento De Stijl , con el que querían «establecer un vocabulario visual compuesto de formas geométricas elementales comprensibles para todos y adaptables a cualquier disciplina». [131] [132] Muchas de sus obras de arte consisten visiblemente en cuadrados y triángulos reglados, a veces también con círculos. Los artistas de De Stijl trabajaron en pintura, mobiliario, diseño de interiores y arquitectura. [131] Después de la disolución de De Stijl, Van Doesburg fundó el movimiento de vanguardia Art Concret , describiendo su Composición aritmética de 1929-1930 , una serie de cuatro cuadrados negros en la diagonal de un fondo cuadrado, como «una estructura que se puede controlar, una superficie definida sin elementos aleatorios ni caprichos individuales», pero «no carente de espíritu, no carente de lo universal y no... vacía ya que hay todo lo que encaja en el ritmo interno». La crítica de arte Gladys Fabre observa que en la pintura se dan dos progresiones: los cuadrados negros crecientes y los fondos alternados. [133]
Las matemáticas de la teselación , los poliedros, la conformación del espacio y la autorreferencia proporcionaron al artista gráfico MC Escher (1898-1972) materiales para sus xilografías que le durarían toda una vida. [134] [135] En el Boceto de la Alhambra , Escher demostró que se puede crear arte con polígonos o formas regulares como triángulos, cuadrados y hexágonos. Escher utilizó polígonos irregulares al teselar el plano y a menudo utilizó reflexiones, reflexiones de deslizamiento y traslaciones para obtener más patrones. Muchas de sus obras contienen construcciones imposibles, realizadas utilizando objetos geométricos que establecen una contradicción entre la proyección en perspectiva y las tres dimensiones, pero que son agradables a la vista humana. El Ascenso y descenso de Escher se basa en la " escalera imposible " creada por el científico médico Lionel Penrose y su hijo, el matemático Roger Penrose . [136] [137] [138]
Algunos de los numerosos dibujos de teselaciones de Escher se inspiraron en conversaciones con el matemático HSM Coxeter sobre geometría hiperbólica . [139] Escher estaba especialmente interesado en cinco poliedros específicos, que aparecen muchas veces en su obra. Los sólidos platónicos (tetraedros, cubos, octaedros, dodecaedros e icosaedros) son especialmente prominentes en Orden y caos y Cuatro sólidos regulares . [140] Estas figuras esteladas a menudo residen dentro de otra figura que distorsiona aún más el ángulo de visión y la conformación de los poliedros y proporciona una obra de arte en perspectiva multifacética. [141]
La complejidad visual de las estructuras matemáticas, como los teselados y los poliedros, ha inspirado una variedad de obras de arte matemáticas. Stewart Coffin fabrica rompecabezas poliédricos en maderas raras y hermosas; George W. Hart trabaja en la teoría de los poliedros y esculpe objetos inspirados en ellos; Magnus Wenninger hace modelos "especialmente hermosos" de complejos poliedros estrellados . [142]
Las perspectivas distorsionadas de la anamorfosis han sido exploradas en el arte desde el siglo XVI, cuando Hans Holbein el Joven incorporó un cráneo severamente distorsionado en su pintura de 1533 Los embajadores . Muchos artistas desde entonces, incluido Escher, han hecho uso de trucos anamórficos. [143]
Las matemáticas de la topología han inspirado a varios artistas en los tiempos modernos. El escultor John Robinson (1935-2007) creó obras como Nudo gordiano y Bandas de la amistad , que muestran la teoría de nudos en bronce pulido. [7] Otras obras de Robinson exploran la topología de los toros . Génesis se basa en los anillos borromeos , un conjunto de tres círculos, de los cuales no hay dos que se enlacen pero en el que toda la estructura no se puede desmontar sin romperse. [144] El escultor Helaman Ferguson crea superficies complejas y otros objetos topológicos . [145] Sus obras son representaciones visuales de objetos matemáticos; El camino óctuple se basa en el grupo lineal especial proyectivo PSL(2,7) , un grupo finito de 168 elementos. [146] [147] La escultora Bathsheba Grossman basa de manera similar su trabajo en estructuras matemáticas. [148] [149] El artista Nelson Saiers incorpora conceptos matemáticos y teoremas en su arte, desde topos y esquemas hasta el teorema de los cuatro colores y la irracionalidad de π . [150]
Un proyecto de investigación de artes liberales examina las conexiones entre las matemáticas y el arte a través de la cinta de Möbius , los flexágonos , el origami y la fotografía panorámica . [151]
Los objetos matemáticos, incluida la variedad de Lorenz y el plano hiperbólico, se han elaborado utilizando artes de fibra , incluido el crochet. [d] [153] La tejedora estadounidense Ada Dietz escribió una monografía de 1949 Expresiones algebraicas en textiles tejidos a mano , definiendo patrones de tejido basados en la expansión de polinomios multivariados . [154] La matemática Daina Taimiņa demostró características del plano hiperbólico tejiendo a crochet en 2001. [155] Esto llevó a Margaret y Christine Wertheim a tejer a crochet un arrecife de coral , que consta de muchos animales marinos como nudibranquios cuyas formas se basan en planos hiperbólicos. [156] El matemático JCP Miller utilizó el autómata celular de la Regla 90 para diseñar tapices que representan árboles y patrones abstractos de triángulos. [157] Los "matemáticos" [158] Pat Ashforth y Steve Plummer utilizan versiones tejidas de objetos matemáticos como hexaflexágonos en su enseñanza, aunque su esponja Menger resultó demasiado problemática para tejer y en su lugar estaba hecha de lona plástica. [159] [160] Su proyecto "mathghans" (afganos para las escuelas) introdujo el tejido en el currículo británico de matemáticas y tecnología. [161] [162]



El modelado está lejos de ser la única forma posible de ilustrar conceptos matemáticos. El Tríptico Stefaneschi de Giotto , 1320, ilustra la recursión en forma de mise en abyme ; el panel central del tríptico contiene, abajo a la izquierda, la figura arrodillada del cardenal Stefaneschi, sosteniendo el tríptico como una ofrenda. [165] Las pinturas metafísicas de Giorgio de Chirico , como su Gran interior metafísico de 1917, exploran la cuestión de los niveles de representación en el arte al representar pinturas dentro de sus pinturas. [166]
El arte puede ejemplificar paradojas lógicas, como en algunas pinturas del surrealista René Magritte , que pueden leerse como bromas semióticas sobre la confusión entre niveles. En La condición humana (1933), Magritte representa un caballete (sobre el lienzo real), que sostiene sin problemas una vista a través de una ventana que está enmarcada por cortinas "reales" en la pintura. De manera similar, la Galería de grabados de Escher (1956) es un grabado que representa una ciudad distorsionada que contiene una galería que contiene recursivamente la imagen, y así ad infinitum . [167] Magritte hizo uso de esferas y cuboides para distorsionar la realidad de una manera diferente, pintándolos junto a una variedad de casas en su Aritmética mental de 1931 como si fueran bloques de construcción para niños, pero del tamaño de una casa. [168] The Guardian observó que la "espeluznante imagen de ciudad de juguetes" profetizaba la usurpación por parte del modernismo de las "cómodas formas tradicionales", pero también juega con la tendencia humana a buscar patrones en la naturaleza . [169]

La última pintura de Salvador Dalí, La cola de golondrina (1983), fue parte de una serie inspirada en la teoría de catástrofes de René Thom . [171] El pintor y escultor español Pablo Palazuelo (1916-2007) se centró en la investigación de la forma. Desarrolló un estilo que describió como la geometría de la vida y la geometría de toda la naturaleza. Con formas geométricas simples con patrones y colores detallados, en obras como Angular I y Automnes , Palazuelo se expresó en transformaciones geométricas. [7]
El artista Adrian Gray practica el equilibrio de piedras , explotando la fricción y el centro de gravedad para crear composiciones sorprendentes y aparentemente imposibles. [172]

Sin embargo, los artistas no necesariamente toman la geometría en sentido literal. Como escribe Douglas Hofstadter en su reflexión de 1980 sobre el pensamiento humano, Gödel, Escher, Bach , a modo de (entre otras cosas) las matemáticas del arte: "La diferencia entre un dibujo de Escher y la geometría no euclidiana es que en esta última se pueden encontrar interpretaciones comprensibles para los términos indefinidos, lo que da como resultado un sistema total comprensible, mientras que en la primera, el resultado final no es conciliable con la propia concepción del mundo, sin importar cuánto tiempo se mire la imagen". Hofstadter analiza la litografía aparentemente paradójica Print Gallery de MC Escher; representa una ciudad costera que contiene una galería de arte que parece contener una pintura de la ciudad costera, existiendo un "bucle extraño o una jerarquía enredada" en los niveles de realidad de la imagen. El propio artista, observa Hofstadter, no es visto; su realidad y su relación con la litografía no son paradójicas. [170] El vacío central de la imagen también ha atraído el interés de los matemáticos Bart de Smit y Hendrik Lenstra , quienes proponen que podría contener una copia de sí misma con efecto Droste , rotada y encogida; esto sería una ilustración más de la recursión más allá de lo señalado por Hofstadter. [173] [174]
El análisis algorítmico de imágenes de obras de arte, por ejemplo mediante espectroscopia de fluorescencia de rayos X , puede revelar información sobre el arte. Estas técnicas pueden descubrir imágenes en capas de pintura que luego cubrió un artista; ayudar a los historiadores del arte a visualizar una obra de arte antes de que se agrietara o se desvaneciera; ayudar a distinguir una copia de un original o distinguir el estilo de pincelada de un maestro del de sus aprendices. [175] [176]

El estilo de pintura por goteo de Jackson Pollock [177] tiene una dimensión fractal definida ; [178] entre los artistas que pueden haber influido en el caos controlado de Pollock , [179] Max Ernst pintó figuras de Lissajous directamente balanceando un cubo perforado de pintura sobre un lienzo. [180]
El informático Neil Dodgson investigó si las pinturas de rayas de Bridget Riley podían caracterizarse matemáticamente y concluyó que, si bien la distancia de separación podía "proporcionar cierta caracterización" y la entropía global funcionaba en algunas pinturas, la autocorrelación fallaba porque los patrones de Riley eran irregulares. La entropía local funcionaba mejor y se correlacionaba bien con la descripción dada por el crítico de arte Robert Kudielka. [181]
La Medida Estética del matemático estadounidense George Birkhoff de 1933 propone una métrica cuantitativa de la calidad estética de una obra de arte. No intenta medir las connotaciones de una obra, como lo que podría significar una pintura, sino que se limita a los "elementos de orden" de una figura poligonal. Birkhoff primero combina (como una suma) cinco de estos elementos: si hay un eje de simetría vertical; si hay equilibrio óptico; cuántas simetrías rotacionales tiene; qué tan parecida es la figura a un papel tapiz; y si hay características insatisfactorias como tener dos vértices demasiado juntos. Esta métrica, O , toma un valor entre −3 y 7. La segunda métrica, C , cuenta los elementos de la figura, que para un polígono es el número de líneas rectas diferentes que contienen al menos uno de sus lados. Birkhoff luego define su medida estética de la belleza de un objeto como O/C . Esto puede interpretarse como un equilibrio entre el placer que da mirar el objeto y la cantidad de esfuerzo necesario para asimilarlo. La propuesta de Birkhoff ha sido criticada de diversas maneras, en particular por intentar poner la belleza en una fórmula, pero él nunca afirmó haberlo hecho. [182]
El arte ha estimulado a veces el desarrollo de las matemáticas, como cuando la teoría de la perspectiva en la arquitectura y la pintura de Brunelleschi inició un ciclo de investigación que condujo al trabajo de Brook Taylor y Johann Heinrich Lambert sobre los fundamentos matemáticos del dibujo en perspectiva, [183] y, en última instancia, a las matemáticas de la geometría proyectiva de Girard Desargues y Jean-Victor Poncelet . [184]
El arte japonés del plegado de papel, el origami, ha sido reelaborado matemáticamente por Tomoko Fusé utilizando módulos , piezas de papel congruentes como cuadrados, y convirtiéndolas en poliedros o teselas. [185] El plegado de papel fue utilizado en 1893 por T. Sundara Rao en sus Ejercicios geométricos de plegado de papel para demostrar pruebas geométricas. [186] Las matemáticas del plegado de papel han sido exploradas en el teorema de Maekawa , [187] el teorema de Kawasaki , [188] y los axiomas de Huzita-Hatori . [189]

Las ilusiones ópticas como la espiral de Fraser demuestran de forma sorprendente las limitaciones de la percepción visual humana, creando lo que el historiador de arte Ernst Gombrich llamó un "truco desconcertante". Las cuerdas blancas y negras que parecen formar espirales son, de hecho, círculos concéntricos . El Op art o estilo de arte óptico de mediados del siglo XX de pintura y gráficos explotó tales efectos para crear la impresión de movimiento y patrones parpadeantes o vibrantes que se ven en la obra de artistas como Bridget Riley , Spyros Horemis, [191] y Victor Vasarely . [192]
Una corriente artística que se remonta a la Antigua Grecia considera a Dios como el geómetra del mundo y, por tanto, a la geometría del mundo como sagrada. La creencia de que Dios creó el universo según un plan geométrico tiene orígenes antiguos. Plutarco atribuyó esta creencia a Platón , escribiendo que «Platón dijo que Dios geometriza continuamente» ( Convivialium disputationum , liber 8,2). Esta imagen ha influido en el pensamiento occidental desde entonces. El concepto platónico derivaba a su vez de una noción pitagórica de armonía en la música, donde las notas estaban espaciadas en proporciones perfectas, correspondientes a las longitudes de las cuerdas de la lira; de hecho, los pitagóricos sostenían que todo estaba ordenado por números. De la misma manera, en el pensamiento platónico, los sólidos regulares o platónicos dictan las proporciones que se encuentran en la naturaleza y en el arte. [193] [194] Una iluminación en el Codex Vindobonensis del siglo XIII muestra a Dios dibujando el universo con un compás, lo que puede hacer referencia a un versículo del Antiguo Testamento: "Cuando él estableció los cielos, yo estaba allí; cuando puso una brújula sobre la faz del abismo" (Proverbios 8:27). [195] En 1596, el astrónomo matemático Johannes Kepler modeló el universo como un conjunto de sólidos platónicos anidados, determinando los tamaños relativos de las órbitas de los planetas. [195] El Anciano de Días de William Blake (que representa a Urizen , la encarnación de la razón y la ley de Blake) y su pintura del físico Isaac Newton , desnudo, encorvado y dibujando con un compás, usan el simbolismo de las brújulas para criticar la razón convencional y el materialismo como de miras estrechas. [196] [197] La Crucifixión (Corpus Hypercubus) de Salvador Dalí de 1954 representa la cruz como un hipercubo , que representa la perspectiva divina con cuatro dimensiones en lugar de las tres habituales. [84] En El sacramento de la última cena (1955) de Dalí, Cristo y sus discípulos están representados dentro de un dodecaedro gigante . [198]
que ilustran la fascinación de Uccello por la perspectiva. Los combatientes en una justa se enfrentan en un campo de batalla plagado de lanzas rotas que han caído en un patrón casi cuadriculado y apuntan hacia un punto de fuga en algún lugar en la distancia.
{{cite book}}: Mantenimiento de CS1: falta la ubicación del editor ( enlace ){{cite book}}: Mantenimiento de CS1: falta la ubicación del editor ( enlace )el Libro I, después de algunas construcciones elementales para introducir la idea de que el tamaño aparente de un objeto es en realidad su ángulo subtendido a la vista, y haciendo referencia a los Elementos Libros I y VI de Euclides y a la Óptica de Euclides, pasa, en la Proposición 13, a la representación de un cuadrado que yace plano en el suelo frente al espectador. ¿Qué debería dibujar realmente el artista? Después de esto, se construyen objetos en el cuadrado (azulejos, por ejemplo, para representar un suelo de baldosas), y los objetos correspondientes se construyen en perspectiva; en el Libro II se erigen prismas sobre estos objetos planos, para representar casas, columnas, etc.; pero la base del método es el cuadrado original, del que se desprende todo lo demás.
La técnica geométrica de construcción de la sección áurea parece haber determinado las decisiones principales de la organización espacial. La sección áurea aparece repetidamente en algunas partes de las medidas del edificio. Se encuentra en la proporción general de la planta y en el dimensionamiento del espacio de oración, el patio y el minarete. La existencia de la sección áurea en algunas partes de la mezquita de Kairuán indica que los elementos diseñados y generados con este principio pueden haber sido realizados en el mismo período.
{{cite journal}}: CS1 maint: URL no apta ( enlace )Pollock murió en 1956, antes de que se descubrieran el caos y los fractales. Por lo tanto, es muy poco probable que Pollock comprendiera conscientemente los fractales que estaba pintando. Sin embargo, su introducción de fractales fue deliberada. Por ejemplo, el color de la capa de anclaje se eligió para producir el contraste más marcado contra el fondo del lienzo y esta capa también ocupa más espacio del lienzo que las otras capas, lo que sugiere que Pollock quería que esta capa de anclaje altamente fractal dominara visualmente la pintura. Además, una vez terminadas las pinturas, cortaba el lienzo para eliminar las regiones cerca del borde donde la densidad del patrón era menos uniforme.
A lo largo de los primeros años de la década de 1980, los patrones de Riley pasaron de ser más regulares a ser más aleatorios (como se caracteriza por la entropía global), sin perder su estructura rítmica (como se caracteriza por la entropía local). Esto refleja la descripción que hace Kudielka de su desarrollo artístico.