
En el estudio matemático de los autómatas celulares , la Regla 90 es un autómata celular elemental basado en la función o exclusiva . Consiste en una matriz unidimensional de celdas, cada una de las cuales puede contener un valor 0 o 1. En cada paso de tiempo, todos los valores se reemplazan simultáneamente por el XOR de sus dos valores vecinos. [1] Martin, Odlyzko y Wolfram (1984) lo llaman "el autómata celular no trivial más simple", [2] y se describe extensamente en el libro de Stephen Wolfram de 2002 A New Kind of Science . [3]
Cuando se inicia con una única célula viva, la Regla 90 tiene un diagrama espacio-temporal en forma de triángulo de Sierpiński . El comportamiento de cualquier otra configuración se puede explicar como una superposición de copias de este patrón, combinadas mediante la función o exclusiva . Cualquier configuración con solo un número finito de células distintas de cero se convierte en un replicador que, con el tiempo, llena la matriz con copias de sí mismo. Cuando la Regla 90 se inicia con una configuración inicial aleatoria , su configuración sigue siendo aleatoria en cada paso de tiempo. Su diagrama espacio-temporal forma muchas "ventanas" triangulares de diferentes tamaños, patrones que se forman cuando una fila consecutiva de células se vuelve simultáneamente cero y luego las células con valor 1 se mueven gradualmente hacia esta fila desde ambos extremos.
Algunos de los primeros estudios de la Regla 90 se realizaron en relación con un problema no resuelto en la teoría de números , la conjetura de Gilbreath , sobre las diferencias de números primos consecutivos . Esta regla también está relacionada con la teoría de números de una manera diferente, a través de la secuencia de Gould . Esta secuencia cuenta el número de celdas distintas de cero en cada paso de tiempo después de iniciar la Regla 90 con una sola celda viva. Sus valores son potencias de dos , con exponentes iguales al número de dígitos distintos de cero en la representación binaria del número de paso. Otras aplicaciones de la Regla 90 han incluido el diseño de tapices .
Cada configuración de la Regla 90 tiene exactamente cuatro predecesores, otras configuraciones que forman la configuración dada después de un solo paso. Por lo tanto, a diferencia de muchos otros autómatas celulares como el Juego de la Vida de Conway , la Regla 90 no tiene Jardín del Edén , una configuración sin predecesores. Proporciona un ejemplo de un autómata celular que es sobreyectivo (cada configuración tiene un predecesor) pero no inyectivo (tiene conjuntos de más de una configuración con el mismo sucesor). Se deduce del teorema del Jardín del Edén que la Regla 90 es localmente inyectiva (todas las configuraciones con el mismo sucesor varían en un número infinito de celdas).

La regla 90 es un autómata celular elemental . Esto significa que consiste en una matriz unidimensional de celdas, cada una de las cuales contiene un único valor binario, ya sea 0 o 1. La asignación de valores a todas las celdas se denomina configuración . El autómata recibe una configuración inicial y luego progresa a través de otras configuraciones en una secuencia de pasos de tiempo discretos. En cada paso, todas las celdas se actualizan simultáneamente. Una regla preestablecida determina el nuevo valor de cada celda en función de su valor anterior y de los valores en sus dos celdas vecinas. Todas las celdas obedecen a la misma regla, que puede darse como una fórmula o como una tabla de reglas que especifica el nuevo valor para cada posible combinación de valores vecinos. [1]
En el caso de la regla 90, el nuevo valor de cada celda es el o exclusivo de los dos valores vecinos. De manera equivalente, el siguiente estado de este autómata en particular se rige por la siguiente tabla de reglas: [1]
El nombre de la Regla 90 proviene de la notación binario-decimal de Stephen Wolfram para las reglas de autómatas celulares unidimensionales. Para calcular la notación de la regla, concatene los nuevos estados en la tabla de reglas en un solo número binario y convierta el número en decimal : 01011010 2 = 90 10 . [1] La Regla 90 también se ha llamado autómata de Sierpiński , debido a la forma característica de triángulo de Sierpiński que genera, [4] y autómata celular de Martin–Odlyzko–Wolfram después de la investigación temprana de Olivier Martin, Andrew M. Odlyzko y Stephen Wolfram (1984) sobre este autómata. [5]
Una configuración en la Regla 90 se puede dividir en dos subconjuntos de celdas que no interactúan entre sí. Uno de estos dos subconjuntos consta de las celdas en posiciones pares en pasos de tiempo pares y las celdas en posiciones impares en pasos de tiempo impares. El otro subconjunto consta de las celdas en posiciones pares en pasos de tiempo impares y las celdas en posiciones impares en pasos de tiempo pares. Cada uno de estos dos subconjuntos se puede ver como un autómata celular con solo su mitad de celdas. [6] La regla para el autómata dentro de cada uno de estos subconjuntos es equivalente (excepto por un cambio de media celda por paso de tiempo) a otro autómata celular elemental , la Regla 102 , en la que el nuevo estado de cada celda es el o exclusivo de su estado anterior y su vecino derecho. Es decir, el comportamiento de la Regla 90 es esencialmente el mismo que el comportamiento de dos copias intercaladas de la Regla 102. [7]
Las reglas 90 y 102 se denominan autómatas celulares aditivos . Esto significa que, si se combinan dos estados iniciales calculando el o exclusivo de cada uno de sus estados, sus configuraciones posteriores se combinarán de la misma manera. En términos más generales, se puede dividir cualquier configuración de la regla 90 en dos subconjuntos con celdas disjuntas no nulas, desarrollar los dos subconjuntos por separado y calcular cada configuración sucesiva del autómata original como el o exclusivo de las configuraciones en los mismos pasos de tiempo de los dos subconjuntos. [2]
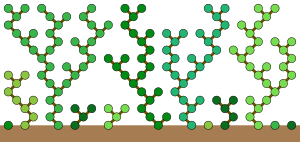
El autómata de la Regla 90 (en su forma equivalente en uno de los dos subconjuntos independientes de celdas alternas) fue investigado a principios de la década de 1970, en un intento de obtener información adicional sobre la conjetura de Gilbreath sobre las diferencias de números primos consecutivos . En el triángulo de números generado a partir de los primos mediante la aplicación repetida del operador de diferencia hacia adelante , parece que la mayoría de los valores son 0 o 2. En particular, la conjetura de Gilbreath afirma que los valores más a la izquierda en cada fila de este triángulo son todos 0 o 2. Cuando una subsecuencia contigua de valores en una fila del triángulo son todos 0 o 2, entonces la Regla 90 se puede utilizar para determinar la subsecuencia correspondiente en la siguiente fila. Miller (1970) explicó la regla mediante una metáfora del crecimiento de los árboles en un bosque, titulando su artículo sobre el tema "Bosques periódicos de árboles atrofiados". En esta metáfora, un árbol comienza a crecer en cada posición de la configuración inicial cuyo valor es 1, y este bosque de árboles crece simultáneamente, hasta una nueva altura sobre el suelo en cada paso de tiempo. Cada celda distinta de cero en cada paso de tiempo representa una posición que está ocupada por una rama de árbol en crecimiento. En cada paso de tiempo sucesivo, una rama puede crecer hacia una de las dos celdas que se encuentran por encima de ella a su izquierda y derecha solo cuando no hay otra rama que compita por la misma celda. Un bosque de árboles que crece según estas reglas tiene exactamente el mismo comportamiento que la Regla 90. [8]
A partir de cualquier configuración inicial de la Regla 90, se puede formar un bosque matemático , un grafo acíclico dirigido en el que cada vértice tiene como máximo una arista saliente, cuyos árboles son los mismos que los árboles de la metáfora de Miller. El bosque tiene un vértice para cada par ( x , i ) tal que la celda x es distinta de cero en el tiempo i . Los vértices en el tiempo 0 no tienen aristas salientes; cada uno forma la raíz de un árbol en el bosque. Para cada vértice ( x , i ) con i distinto de cero, su arista saliente va a ( x ± 1, i − 1) , el único vecino distinto de cero de x en el paso de tiempo i − 1 . Miller observó que estos bosques desarrollan "claros" triangulares, regiones del diagrama espacio-temporal sin celdas distintas de cero delimitadas por una arista inferior plana y lados diagonales. Este tipo de claro se forma cuando una secuencia consecutiva de células se vuelve cero simultáneamente en un paso de tiempo, y luego (en la metáfora del árbol) las ramas crecen hacia adentro, cubriendo eventualmente nuevamente las células de la secuencia. [8]
En condiciones iniciales aleatorias, los límites entre los árboles formados de esta manera se desplazan en un patrón aparentemente aleatorio y, con frecuencia, los árboles mueren por completo. Pero mediante la teoría de los registros de desplazamiento, él y otros pudieron encontrar condiciones iniciales en las que todos los árboles permanecen vivos para siempre, el patrón de crecimiento se repite periódicamente y se puede garantizar que todos los claros permanezcan limitados en tamaño. [8] [9] Miller utilizó estos patrones repetitivos para formar los diseños de tapices . Algunos de los tapices de Miller representan árboles físicos; otros visualizan el autómata de la Regla 90 utilizando patrones abstractos de triángulos. [8]

El diagrama espacio-temporal de la Regla 90 es un gráfico en el que la fila i registra la configuración del autómata en el paso i . Cuando el estado inicial tiene una sola celda distinta de cero, este diagrama tiene la apariencia del triángulo de Sierpinski , un fractal formado al combinar triángulos en triángulos más grandes. Las reglas 18, 22, 26, 82, 146, 154, 210 y 218 también generan triángulos de Sierpinski a partir de una sola celda, sin embargo, no todos estos se crean de manera completamente idéntica. Una forma de explicar esta estructura utiliza el hecho de que, en la Regla 90, cada celda es la exclusiva o de sus dos vecinas. Debido a que esto es equivalente a la adición módulo -2, esto genera la versión módulo-2 del triángulo de Pascal . El diagrama tiene un 1 donde el triángulo de Pascal tiene un número impar , y un 0 donde el triángulo de Pascal tiene un número par . Esta es una versión discreta del triángulo de Sierpiński. [1] [10]
El número de células vivas en cada fila de este patrón es una potencia de dos . En la fila i , es igual a 2 k , donde k es el número de dígitos distintos de cero en la representación binaria del número i . La secuencia de estos números de células vivas,
Se conoce como secuencia de Gould . La única célula viva de la configuración inicial es un patrón de dientes de sierra . Esto significa que en algunos pasos de tiempo la cantidad de células vivas crece arbitrariamente, mientras que en otros vuelve a solo dos células vivas, con una frecuencia infinita. La tasa de crecimiento de este patrón tiene una forma característica de onda de dientes de sierra creciente que se puede utilizar para reconocer procesos físicos que se comportan de manera similar a la Regla 90. [4]
El triángulo de Sierpiński también se presenta de una manera más sutil en la evolución de cualquier configuración en la Regla 90. En cualquier paso de tiempo i en la evolución de la Regla, el estado de cualquier celda puede calcularse como el o exclusivo de un subconjunto de las celdas en la configuración inicial. Ese subconjunto tiene la misma forma que la fila i del triángulo de Sierpiński. [11]
En el triángulo de Sierpiński, para cualquier entero i , las filas numeradas por múltiplos de 2 i tienen celdas distintas de cero espaciadas al menos 2 i unidades entre sí. Por lo tanto, debido a la propiedad aditiva de la Regla 90, si una configuración inicial consiste en un patrón finito P de celdas distintas de cero con un ancho menor que 2 i , entonces en pasos que son múltiplos de 2 i , la configuración consistirá en copias de P espaciadas al menos 2 i unidades de inicio a inicio. Este espaciamiento es lo suficientemente amplio para evitar que las copias interfieran entre sí. El número de copias es el mismo que el número de celdas distintas de cero en la fila correspondiente del triángulo de Sierpiński. Por lo tanto, en esta regla, cada patrón es un replicador : genera múltiples copias de sí mismo que se extienden por la configuración, llenando eventualmente toda la matriz. Otras reglas, como el constructor universal de Von Neumann , el autómata celular de Codd y los bucles de Langton, también tienen replicadores que funcionan mediante el transporte y la copia de una secuencia de instrucciones para construirse a sí mismos. En cambio, la replicación en la regla 90 es trivial y automática. [12]
En la Regla 90, en una red unidimensional infinita, cada configuración tiene exactamente cuatro configuraciones predecesoras. Esto se debe a que, en una predecesora, dos celdas consecutivas pueden tener cualquier combinación de estados, pero una vez que se eligen los estados de esas dos celdas, solo hay una elección consistente para los estados de las celdas restantes. Por lo tanto, no hay Jardín del Edén en la Regla 90, una configuración sin predecesoras. La configuración de la Regla 90 que consiste en una sola celda distinta de cero (con todas las demás celdas cero) no tiene predecesoras que tengan un número finito de distintos de cero. Sin embargo, esta configuración no es un Jardín del Edén porque sí tiene predecesoras con un número infinito de distintos de cero. [13]
El hecho de que cada configuración tenga un predecesor puede resumirse diciendo que la Regla 90 es sobreyectiva . La función que asigna cada configuración a su sucesora es, matemáticamente, una función sobreyectiva. La Regla 90 tampoco es inyectiva . En una regla inyectiva, cada dos configuraciones diferentes tienen sucesores diferentes, pero la Regla 90 tiene pares de configuraciones con el mismo sucesor. La Regla 90 proporciona un ejemplo de un autómata celular que es sobreyectivo pero no inyectivo. El teorema del Jardín del Edén de Moore y Myhill implica que todo autómata celular inyectivo debe ser sobreyectivo, pero este ejemplo muestra que lo inverso no es cierto. [13] [14]
Como cada configuración tiene sólo un número limitado de predecesoras, la evolución de la Regla 90 preserva la entropía de cualquier configuración. En particular, si se selecciona una configuración inicial infinita eligiendo el estado de cada celda de forma independiente al azar, y cada uno de los dos estados tiene la misma probabilidad de ser seleccionado, entonces cada configuración posterior puede describirse exactamente con la misma distribución de probabilidad. [2]
Muchos otros autómatas celulares y otros sistemas computacionales son capaces de emular el comportamiento de la Regla 90. Por ejemplo, una configuración en la Regla 90 puede ser traducida a una configuración en el autómata celular elemental diferente Regla 22. La traducción reemplaza cada celda de la Regla 90 por tres celdas consecutivas de la Regla 22. Estas celdas son todas cero si la celda de la Regla 90 es en sí misma cero. Una celda de la Regla 90 distinta de cero se traduce en un uno seguido de dos ceros. Con esta transformación, cada seis pasos del autómata de la Regla 22 simulan un solo paso del autómata de la Regla 90. También son posibles simulaciones directas similares de la Regla 90 para los autómatas celulares elementales Regla 45 y Regla 126, para ciertos sistemas de reescritura de cadenas y sistemas de etiquetas , y en algunos autómatas celulares bidimensionales, incluido Wireworld . La Regla 90 también puede simularse a sí misma de la misma manera. Si cada celda de una configuración de la Regla 90 se reemplaza por un par de celdas consecutivas, la primera conteniendo el valor de la celda original y la segunda conteniendo cero, entonces esta configuración duplicada tiene el mismo comportamiento que la configuración original a la mitad de la velocidad. [15]
Se sabe que otros autómatas celulares admiten replicadores, patrones que hacen copias de sí mismos, y la mayoría comparten el mismo comportamiento que en el modelo de crecimiento de árbol de la Regla 90. Se coloca una nueva copia a cada lado del patrón del replicador, siempre que el espacio esté vacío. Sin embargo, si dos replicadores intentan copiarse a sí mismos en la misma posición, el espacio permanece vacío. En cualquier caso, los replicadores desaparecen, dejando que sus copias continúen con la replicación. Un ejemplo estándar de este comportamiento es el patrón de "pasta con moños" en la regla bidimensional HighLife . Esta regla se comporta en muchos sentidos como el Juego de la Vida de Conway, pero un replicador tan pequeño no existe en Life. Siempre que un autómata admita replicadores con el mismo patrón de crecimiento, se pueden utilizar matrices unidimensionales de replicadores para simular la Regla 90. [16] La Regla 90 (en filas finitas de células) también se puede simular mediante los osciladores de bloque del autómata celular bidimensional similar a Life B36/S125, también llamado "2x2", y el comportamiento de la Regla 90 se puede utilizar para caracterizar los posibles períodos de estos osciladores. [17]