Exponenciación

Arithmetic operation

Gráficas de y = b ^x para varias bases b :  base 10,   base e,   base 2,   base ​1/2⁠ .Cada curva pasa por el punto(0, 1)porque cualquier número distinto de cero elevado a la potencia0es1.Enx= 1, el valor deyes igual a la base porque cualquier número elevado a la potencia1es el número mismo.

En matemáticas , la exponenciación es una operación que involucra dos números : la base y el exponente o potencia . La exponenciación se escribe como b ⁿ , donde b es la base y n es la potencia ; esto se pronuncia como " b (elevado) a la (potencia de) n ". ^[1] Cuando n es un entero positivo , la exponenciación corresponde a la multiplicación repetida de la base: es decir, b ⁿ es el producto de multiplicar n bases: ^[1] $${\displaystyle b^{n}=\underbrace {b\times b\times \dots \times b\times b} _{n{\text{ times}}}.}$$

El exponente se muestra generalmente como un superíndice a la derecha de la base. En ese caso, b ⁿ se llama " b elevado a la n -ésima potencia", " b (elevado) a la n- ésima potencia ", "la n - ésima potencia de b ", " b elevado a la n -ésima potencia" ^[2] o, de forma más breve, " b elevado a la n -ésima potencia".

Partiendo del hecho básico indicado anteriormente de que, para cualquier entero positivo , las ocurrencias de todos se multiplican entre sí, se deducen directamente otras propiedades de la exponenciación. En particular: ^{[nb 1]} ${\displaystyle n}$ ${\displaystyle b^{n}}$ ${\displaystyle n}$ ${\displaystyle b}$

$${\displaystyle {\begin{aligned}b^{n+m}&=\underbrace {b\times \dots \times b} _{n+m{\text{ times}}}\\[1ex]&=\underbrace {b\times \dots \times b} _{n{\text{ times}}}\times \underbrace {b\times \dots \times b} _{m{\text{ times}}}\\[1ex]&=b^{n}\times b^{m}\end{aligned}}}$$

En otras palabras, al multiplicar una base elevada a un exponente por la misma base elevada a otro exponente, los exponentes se suman. A partir de esta regla básica de que los exponentes se suman, podemos deducir que debe ser igual a 1 para cualquier , de la siguiente manera. Para cualquier , . Dividiendo ambos lados por se obtiene . ${\displaystyle b^{0}}$ ${\displaystyle b\neq 0}$ ${\displaystyle n}$ ${\displaystyle b^{0}\times b^{n}=b^{0+n}=b^{n}}$ ${\displaystyle b^{n}}$ ${\displaystyle b^{0}=b^{n}/b^{n}=1}$

El hecho de que se puede derivar de manera similar de la misma regla. Por ejemplo, . Tomando la raíz cúbica de ambos lados se obtiene . ${\displaystyle b^{1}=b}$ ${\displaystyle (b^{1})^{3}=b^{1}\times b^{1}\times b^{1}=b^{1+1+1}=b^{3}}$ ${\displaystyle b^{1}=b}$

La regla de que la multiplicación hace que los exponentes se sumen también se puede utilizar para derivar las propiedades de los exponentes enteros negativos. Consideremos la cuestión de qué debería significar. Para respetar la regla de que "los exponentes se suman", debe darse el caso de que . Dividiendo ambos lados por obtenemos , que se puede escribir de forma más sencilla como , utilizando el resultado anterior de que . Por un argumento similar, . ${\displaystyle b^{-1}}$ ${\displaystyle b^{-1}\times b^{1}=b^{-1+1}=b^{0}=1}$ ${\displaystyle b^{1}}$ ${\displaystyle b^{-1}=1/b^{1}}$ ${\displaystyle b^{-1}=1/b}$ ${\displaystyle b^{1}=b}$ ${\displaystyle b^{-n}=1/b^{n}}$

Las propiedades de los exponentes fraccionarios también se derivan de la misma regla. Por ejemplo, supongamos que consideramos y preguntamos si hay algún exponente adecuado, al que podamos llamar , tal que . De la definición de la raíz cuadrada, tenemos que . Por lo tanto, el exponente debe ser tal que . Usando el hecho de que la multiplicación hace que los exponentes se sumen, obtenemos . El en el lado derecho también se puede escribir como , dando . Igualando los exponentes en ambos lados, tenemos . Por lo tanto, , entonces . ${\displaystyle {\sqrt {b}}}$ ${\displaystyle r}$ ${\displaystyle b^{r}={\sqrt {b}}}$ ${\displaystyle {\sqrt {b}}\times {\sqrt {b}}=b}$ ${\displaystyle r}$ ${\displaystyle b^{r}\times b^{r}=b}$ ${\displaystyle b^{r+r}=b}$ ${\displaystyle b}$ ${\displaystyle b^{1}}$ ${\displaystyle b^{r+r}=b^{1}}$ ${\displaystyle r+r=1}$ ${\displaystyle r={\tfrac {1}{2}}}$ ${\displaystyle {\sqrt {b}}=b^{1/2}}$

La definición de exponenciación se puede ampliar para admitir cualquier exponente real o complejo . La exponenciación por exponentes enteros también se puede definir para una amplia variedad de estructuras algebraicas, incluidas las matrices .

La exponenciación se utiliza ampliamente en muchos campos, incluidos la economía , la biología , la química , la física y la informática , con aplicaciones como el interés compuesto , el crecimiento poblacional , la cinética de las reacciones químicas , el comportamiento de las ondas y la criptografía de clave pública .

Etimología

El término exponente tiene su origen en el latín exponentem , participio presente de exponere , que significa "poner adelante". ^[3] El término potencia ( latín : potentia, potestas, dignitas ) es una traducción errónea ^{[4] [5]} del griego antiguo δύναμις ( dúnamis , aquí: "amplificación" ^[4] ) utilizado por el matemático griego Euclides para el cuadrado de una línea, ^[6] siguiendo a Hipócrates de Quíos . ^[7]

Historia

Antigüedad

El contador de arena

En The Sand Reckoner , Arquímedes demostró la ley de los exponentes, 10 ^a · 10 ^b = 10 ^{a + b} , necesaria para manipular potencias de 10. ^[8] Luego utilizó potencias de 10 para estimar la cantidad de granos de arena que pueden contener el universo.

Edad de oro islámica

MalyKaaba("cuadrado" y "cubo")

En el siglo IX, el matemático persa Al-Khwarizmi utilizó los términos مَال ( māl , "posesiones", "propiedad") para un cuadrado —los musulmanes, "como la mayoría de los matemáticos de aquellos tiempos y anteriores, pensaban en un número cuadrado como una representación de un área, especialmente de tierra, por lo tanto, propiedad" ^[9] —y كَعْبَة ( Kaʿbah , "cubo") para un cubo , que los matemáticos islámicos posteriores representaron en notación matemática como las letras mīm (m) y kāf (k), respectivamente, en el siglo XV, como se ve en la obra de Abu'l-Hasan ibn Ali al-Qalasadi . ^[10]

Siglo XV-XVIII

Introducción de exponentes

Nicolas Chuquet utilizó una forma de notación exponencial en el siglo XV, por ejemplo 12 ² para representar 12 x ² . ^[11] Esto fue utilizado más tarde por Henricus Grammateus y Michael Stifel en el siglo XVI. A finales del siglo XVI, Jost Bürgi utilizaría números romanos para exponentes de una manera similar a la de Chuquet, por ejemploiii4para 4 x ³ . ^[12]

"Exponente"; "cuadrado" y "cubo"

La palabra exponente fue acuñada en 1544 por Michael Stifel. ^{[13] [14]} En el siglo XVI, Robert Recorde utilizó los términos cuadrado, cubo, zenzizenzic ( cuarta potencia ), sursólido (quinto), zenzicubo (sexto), segundo sursólido (séptimo) y zenzizenzizenzic (octavo). ^[9] Bicuadrado también se ha utilizado para referirse a la cuarta potencia.

Notación exponencial moderna

En 1636, James Hume utilizó en esencia la notación moderna, cuando en L'algèbre de Viète escribió A ⁱⁱⁱ por A ³ . ^[15] A principios del siglo XVII, la primera forma de nuestra notación exponencial moderna fue introducida por René Descartes en su texto titulado La Géométrie ; allí, la notación se introduce en el Libro I. ^[16]

Yo designo... aa , o un ² al multiplicar a por sí mismo; y un ³ al multiplicarlo una vez más por a , y así hasta el infinito.

—  René Descartes, La geometría

Algunos matemáticos (como Descartes) utilizaban exponentes solo para potencias mayores que dos, prefiriendo representar los cuadrados como multiplicaciones repetidas. Así, escribían los polinomios , por ejemplo, como ax + bxx + cx ³ + d .

"Índices"

Samuel Jeake introdujo el término índices en 1696. ^[6] El término involución se usaba como sinónimo del término índices , pero su uso había disminuido ^[17] y no debe confundirse con su significado más común .

Exponentes variables, exponentes no enteros

En 1748, Leonhard Euler introdujo exponentes variables y, implícitamente, exponentes no enteros escribiendo:

Consideremos exponenciales o potencias en las que el propio exponente es una variable. Es claro que cantidades de este tipo no son funciones algebraicas , ya que en ellas los exponentes deben ser constantes. ^[18]

Terminología

La expresión b ² = b · b se llama "el cuadrado de b " o " b al cuadrado", porque el área de un cuadrado con lado b es b ² . (Es cierto que también podría llamarse " b elevado a la segunda potencia", pero "el cuadrado de b " y " b elevado al cuadrado" están tan arraigados por la tradición y la conveniencia que " b elevado a la segunda potencia" tiende a sonar inusual o torpe.)

De manera similar, la expresión b ³ = b · b · b se llama "el cubo de b " o " b al cubo", porque el volumen de un cubo con lados b es b ³ .

Cuando un exponente es un entero positivo , ese exponente indica cuántas copias de la base se multiplican entre sí. Por ejemplo, 3 ⁵ = 3 · 3 · 3 · 3 · 3 = 243. La base 3 aparece 5 veces en la multiplicación, porque el exponente es 5. Aquí, 243 es la quinta potencia de 3 , o 3 elevado a la quinta potencia .

La palabra "elevado" suele omitirse, y a veces también "potencia", por lo que 3 ⁵ puede leerse simplemente "3 elevado a la 5", o "3 elevado a la 5". Por lo tanto, la potencia b ⁿ puede expresarse como " b elevado a la n ", " b elevado a la n ", " b elevado a la n " o, de forma más breve, como " b elevado a la n ".

Exponentes enteros

La operación de exponenciación con exponentes enteros puede definirse directamente a partir de operaciones aritméticas elementales .

Exponentes positivos

La definición de la exponenciación como una multiplicación iterada se puede formalizar mediante el uso de inducción , ^[19] y esta definición se puede utilizar tan pronto como se tenga una multiplicación asociativa :

El caso base es

${\displaystyle b^{1}=b}$

y la recurrencia es

${\displaystyle b^{n+1}=b^{n}\cdot b.}$

La asociatividad de la multiplicación implica que para cualesquiera números enteros positivos m y n ,

${\displaystyle b^{m+n}=b^{m}\cdot b^{n},}$

y

${\displaystyle (b^{m})^{n}=b^{mn}.}$

Exponente cero

Como se mencionó anteriormente, un número (distinto de cero) elevado a la potencia 0 es 1 : ^{[20] [1]}

${\displaystyle b^{0}=1.}$

Este valor también se obtiene por la convención del producto vacío , que se puede utilizar en cualquier estructura algebraica con una multiplicación que tenga una identidad . De esta manera la fórmula

${\displaystyle b^{m+n}=b^{m}\cdot b^{n}}$

También es válido para . ${\displaystyle n=0}$

El caso de 0 ⁰ es controvertido. En contextos en los que solo se consideran potencias enteras, generalmente se asigna el valor 1 a 0 ^0, pero, en caso contrario, la elección de asignarle un valor y qué valor asignar puede depender del contexto. Para obtener más detalles, consulte Cero elevado a la potencia de cero .

Exponentes negativos

La exponenciación con exponentes negativos se define por la siguiente identidad, que es válida para cualquier entero n y b distinto de cero :

${\displaystyle b^{-n}={\frac {1}{b^{n}}}}$. ^[1]

Elevar 0 a un exponente negativo no está definido pero, en algunas circunstancias, puede interpretarse como infinito ( ). ^[21] ${\displaystyle \infty }$

Esta definición de exponenciación con exponentes negativos es la única que permite extender la identidad a exponentes negativos (consideremos el caso ). ${\displaystyle b^{m+n}=b^{m}\cdot b^{n}}$ ${\displaystyle m=-n}$

La misma definición se aplica a los elementos invertibles en un monoide multiplicativo , es decir, una estructura algebraica , con una multiplicación asociativa y una identidad multiplicativa denotada 1 (por ejemplo, las matrices cuadradas de una dimensión dada). En particular, en una estructura de este tipo, el inverso de un elemento invertible x se denota de manera estándar ${\displaystyle x^{-1}.}$

Identidades y propiedades

Las siguientes identidades , a menudo llamadasLas reglas de los exponentes se aplican a todos los exponentes enteros, siempre que la base no sea cero:^[1]

${\displaystyle {\begin{aligned}b^{m+n}&=b^{m}\cdot b^{n}\\\left(b^{m}\right)^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b^{n}\cdot c^{n}\end{aligned}}}$

A diferencia de la suma y la multiplicación, la exponenciación no es conmutativa . Por ejemplo, 2 ³ = 8 ≠ 3 ² = 9. Además, a diferencia de la suma y la multiplicación, la exponenciación no es asociativa . Por ejemplo, (2 ³ ) ² = 8 ² = 64 , mientras que 2 ^{(3 2 )} = 2 ⁹ = 512. Sin paréntesis, el orden convencional de operaciones para la exponenciación serial en notación de superíndice es de arriba hacia abajo (o asociativa por la derecha ), no de abajo hacia arriba ^{[22] [23] [24]} (o asociativa por la izquierda ). Es decir,

${\displaystyle b^{p^{q}}=b^{\left(p^{q}\right)},}$

que, en general, es diferente de

${\displaystyle \left(b^{p}\right)^{q}=b^{pq}.}$

Potencias de una suma

Las potencias de una suma normalmente se pueden calcular a partir de las potencias de los sumandos mediante la fórmula binomial.

${\displaystyle (a+b)^{n}=\sum _{i=0}^{n}{\binom {n}{i}}a^{i}b^{n-i}=\sum _{i=0}^{n}{\frac {n!}{i!(n-i)!}}a^{i}b^{n-i}.}$

Sin embargo, esta fórmula es verdadera solo si los sumandos conmutan (es decir, que ab = ba ), lo que está implícito si pertenecen a una estructura que es conmutativa . De lo contrario, si a y b son, digamos, matrices cuadradas del mismo tamaño, esta fórmula no se puede utilizar. De ello se deduce que en álgebra computacional , muchos algoritmos que involucran exponentes enteros deben cambiarse cuando las bases de exponenciación no conmutan. Algunos sistemas de álgebra computacional de propósito general usan una notación diferente (a veces ^^ en lugar de ^ ) para la exponenciación con bases no conmutativas, que entonces se llama exponenciación no conmutativa .

Interpretación combinatoria

Para los números enteros no negativos n y m , el valor de n ^m es el número de funciones de un conjunto de m elementos a un conjunto de n elementos (véase exponenciación cardinal ). Dichas funciones se pueden representar como m - tuplas de un conjunto de n - elementos (o como palabras de m - letras de un alfabeto de n - letras). En la siguiente tabla se dan algunos ejemplos de valores particulares de m y n :

Bases particulares

Potencias de diez

En el sistema de numeración decimal , las potencias enteras de 10 se escriben como el dígito 1 seguido o precedido por una cantidad de ceros determinada por el signo y la magnitud del exponente. Por ejemplo,10 ³ =1000 y10 ⁻⁴ =0,0001 .

La exponenciación con base 10 se utiliza en notación científica para indicar números grandes o pequeños. Por ejemplo,299 792 458  m/s (la velocidad de la luz en el vacío, en metros por segundo ) se puede escribir como2,997 924 58 × 10 ⁸  m/s y luego se aproxima como2,998 × 10 ⁸  m/s .

Los prefijos del SI basados ​​en potencias de 10 también se utilizan para describir cantidades pequeñas o grandes. Por ejemplo, el prefijo kilo significa10 ³ =1000 , entonces un kilómetro es1000 metros .

Potencias de dos

Las primeras potencias negativas de 2 se utilizan comúnmente y tienen nombres especiales, por ejemplo: mitad y cuarto .

Las potencias de 2 aparecen en ^la teoría de conjuntos , ya que un conjunto con n miembros tiene un conjunto potencia , el conjunto de todos sus subconjuntos , que tiene 2n miembros.

Las potencias enteras de 2 son importantes en informática . Las potencias enteras positivas 2 ⁿ dan el número de valores posibles para un número binario entero de n bits ; por ejemplo, un byte puede tomar 2 ⁸ = 256 valores diferentes. El sistema de numeración binario expresa cualquier número como una suma de potencias de 2 , y lo denota como una secuencia de 0 y 1 , separados por un punto binario , donde 1 indica una potencia de 2 que aparece en la suma; el exponente está determinado por el lugar de este 1 : los exponentes no negativos son el rango del 1 a la izquierda del punto (empezando desde 0 ), y los exponentes negativos están determinados por el rango a la derecha del punto.

Potencias de uno

Toda potencia de uno es igual a: 1 ⁿ = 1. Esto es cierto incluso si n es negativo.

La primera potencia de un número es el número mismo: n ¹ = n .

Potencias de cero

Si el exponente n es positivo ( n > 0 ), la n- ésima potencia de cero es cero: 0 ⁿ = 0 .

Si el exponente n es negativo ( n < 0 ), la n- ésima potencia de cero 0 ⁿ no está definida, porque debe ser igual a − n > 0 , y esto sería de acuerdo a lo anterior. ${\displaystyle 1/0^{-n}}$ ${\displaystyle 1/0}$

La expresión 0 0 se define como 1 o se deja sin definir.

Potencias de menos uno

Si n es un entero par, entonces (−1) ⁿ = 1. Esto se debe a que un número negativo multiplicado por otro número negativo cancela el signo y, por lo tanto, da un número positivo.

Si n es un entero impar, entonces (−1) ⁿ = −1 . Esto se debe a que quedará un −1 después de eliminar los pares −1 .

Por este motivo, las potencias de −1 son útiles para expresar secuencias alternadas . Para un análisis similar de las potencias del número complejo i , véase § Raíces n-ésimas de un número complejo .

Grandes exponentes

El límite de una secuencia de potencias de un número mayor que uno diverge; en otras palabras, la secuencia crece sin límite:

b ⁿ → ∞ cuando n → ∞ cuando b > 1

Esto puede leerse como " b elevado a n tiende a +∞ cuando n tiende a infinito cuando b es mayor que uno".

Las potencias de un número con valor absoluto menor que uno tienden a cero:

b ⁿ → 0 cuando n → ∞ cuando | b | < 1

Cualquier potencia de uno es siempre uno:

b ⁿ = 1 para todo n si b = 1

Las potencias de –1 alternan entre 1 y –1 a medida que n alterna entre par e impar, y por lo tanto no tienden a ningún límite a medida que n crece.

Si b < –1 , b ⁿ alterna entre números positivos y negativos cada vez mayores a medida que n alterna entre pares e impares, y por lo tanto no tiende a ningún límite a medida que n crece.

Si el número exponencial varía mientras tiende a 1 a medida que el exponente tiende a infinito, entonces el límite no es necesariamente uno de los anteriores. Un caso particularmente importante es

(1 + 1/ n ) ⁿ → e como n → ∞

Véase § Función exponencial a continuación.

Otros límites, en particular los de las expresiones que toman una forma indeterminada , se describen en el § Límites de las potencias más adelante.

Funciones de potencia

Funciones de potencia para n = 1, 3, 5

Funciones de potencia para n = 2, 4, 6

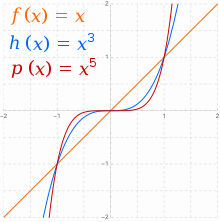
Las funciones reales de la forma , donde , a veces se denominan funciones potencia. ^[25] Cuando es un número entero y , existen dos familias primarias: para par, y para impar. En general , para , cuando es par tenderá hacia el infinito positivo con el aumento de , y también hacia el infinito positivo con la disminución de . Todos los gráficos de la familia de funciones potencia pares tienen la forma general de , aplanándose más en el medio a medida que aumenta. ^[26] Las funciones con este tipo de simetría ( ) se denominan funciones pares . ${\displaystyle f(x)=cx^{n}}$ ${\displaystyle c\neq 0}$ ${\displaystyle n}$ ${\displaystyle n\geq 1}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle c>0}$ ${\displaystyle n}$ ${\displaystyle f(x)=cx^{n}}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y=cx^{2}}$ ${\displaystyle n}$ ${\displaystyle f(-x)=f(x)}$

Cuando es impar, el comportamiento asintótico de se invierte de positivo a negativo . Para , también tenderá hacia el infinito positivo con el aumento de , pero hacia el infinito negativo con la disminución de . Todos los gráficos de la familia de funciones de potencia impares tienen la forma general de , aplanándose más en el medio a medida que aumenta y perdiendo toda planitud allí en la línea recta para . Las funciones con este tipo de simetría ( ) se denominan funciones impares . ${\displaystyle n}$ ${\displaystyle f(x)}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle c>0}$ ${\displaystyle f(x)=cx^{n}}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y=cx^{3}}$ ${\displaystyle n}$ ${\displaystyle n=1}$ ${\displaystyle f(-x)=-f(x)}$

Para , el comportamiento asintótico opuesto es cierto en cada caso. ^[26] ${\displaystyle c<0}$

Tabla de potencias de dígitos decimales

Exponentes racionales

De arriba a abajo: x ^1/8 , x ^1/4 , x ^1/2 , x ¹ , x ² , x ⁴ , x ⁸ .

Si x es un número real no negativo , y n es un entero positivo, o denota la única raíz n- ésima real positiva de x , es decir, el único número real positivo y tal que ${\displaystyle x^{1/n}}$ ${\displaystyle {\sqrt[{n}]{x}}}$ ${\displaystyle y^{n}=x.}$

Si x es un número real positivo, y es un número racional , con p y q > 0 enteros, entonces se define como ${\displaystyle {\frac {p}{q}}}$ ${\textstyle x^{p/q}}$

${\displaystyle x^{\frac {p}{q}}=\left(x^{p}\right)^{\frac {1}{q}}=(x^{\frac {1}{q}})^{p}.}$

La igualdad a la derecha se puede derivar estableciendo y escribiendo ${\displaystyle y=x^{\frac {1}{q}},}$ ${\displaystyle (x^{\frac {1}{q}})^{p}=y^{p}=\left((y^{p})^{q}\right)^{\frac {1}{q}}=\left((y^{q})^{p}\right)^{\frac {1}{q}}=(x^{p})^{\frac {1}{q}}.}$

Si r es un número racional positivo, 0 ^r = 0 , por definición.

Todas estas definiciones son necesarias para extender la identidad a exponentes racionales. ${\displaystyle (x^{r})^{s}=x^{rs}}$

Por otra parte, existen problemas con la extensión de estas definiciones a bases que no son números reales positivos. Por ejemplo, un número real negativo tiene una raíz n- ésima real, que es negativa, si n es impar , y no tiene raíz real si n es par. En el último caso, no se puede satisfacer la raíz n- ésima compleja que se elija para la identidad . Por ejemplo, ${\displaystyle x^{\frac {1}{n}},}$ ${\displaystyle (x^{a})^{b}=x^{ab}}$

${\displaystyle \left((-1)^{2}\right)^{\frac {1}{2}}=1^{\frac {1}{2}}=1\neq (-1)^{2\cdot {\frac {1}{2}}}=(-1)^{1}=-1.}$

Consulte § Exponentes reales y § Potencias no enteras de números complejos para obtener detalles sobre la forma en que se pueden resolver estos problemas.

Exponentes reales

Para los números reales positivos, la exponenciación a potencias reales se puede definir de dos maneras equivalentes, ya sea extendiendo las potencias racionales a los reales por continuidad ( § Límites de exponentes racionales , a continuación), o en términos del logaritmo de la base y la función exponencial ( § Potencias mediante logaritmos , a continuación). El resultado es siempre un número real positivo, y las identidades y propiedades mostradas anteriormente para exponentes enteros siguen siendo verdaderas con estas definiciones para exponentes reales. La segunda definición se utiliza más comúnmente, ya que se generaliza directamente a exponentes complejos .

Por otra parte, la exponenciación a una potencia real de un número real negativo es mucho más difícil de definir de manera consistente, ya que puede ser no real y tener varios valores. Se puede elegir uno de estos valores, llamado valor principal , pero no hay elección del valor principal para el cual se calcula la identidad.

${\displaystyle \left(b^{r}\right)^{s}=b^{rs}}$

es verdadera; véase § Falla de identidades de potencia y logaritmo . Por lo tanto, la exponenciación con una base que no es un número real positivo generalmente se considera como una función multivaluada .

Límites de exponentes racionales

El límite de e ^{1/ n} es e ⁰ = 1 cuando n tiende al infinito.

Dado que cualquier número irracional puede expresarse como el límite de una secuencia de números racionales, la exponenciación de un número real positivo b con un exponente real arbitrario x puede definirse por continuidad con la regla ^[27]

${\displaystyle b^{x}=\lim _{r(\in \mathbb {Q} )\to x}b^{r}\quad (b\in \mathbb {R} ^{+},\,x\in \mathbb {R} ),}$

donde el límite se toma únicamente sobre valores racionales de r . Este límite existe para cada b positivo y cada x real .

Por ejemplo, si x = π , la representación decimal no terminal π = 3,14159... y la monotonía de las potencias racionales se puede utilizar para obtener intervalos acotados por potencias racionales que sean tan pequeños como se desee, y deben contener ${\displaystyle b^{\pi }:}$

${\displaystyle \left[b^{3},b^{4}\right],\left[b^{3.1},b^{3.2}\right],\left[b^{3.14},b^{3.15}\right],\left[b^{3.141},b^{3.142}\right],\left[b^{3.1415},b^{3.1416}\right],\left[b^{3.14159},b^{3.14160}\right],\ldots }$

Por lo tanto, los límites superiores y los límites inferiores de los intervalos forman dos secuencias que tienen el mismo límite, denotado ${\displaystyle b^{\pi }.}$

Esto define para cada b positivo y x real como una función continua de b y x . Véase también Expresión bien definida . ^[28] ${\displaystyle b^{x}}$

Función exponencial

La función exponencial se define a menudo como donde es el número de Euler . Para evitar el razonamiento circular , esta definición no se puede utilizar aquí. Por lo tanto, se da una definición de la función exponencial, denotada como y del número de Euler, que se basan únicamente en la exponenciación con exponentes enteros positivos. Luego se esboza una prueba de que, si se utiliza la definición de exponenciación dada en las secciones anteriores, se tiene ${\displaystyle x\mapsto e^{x},}$ ${\displaystyle e\approx 2.718}$ ${\displaystyle \exp(x),}$

${\displaystyle \exp(x)=e^{x}.}$

Hay muchas formas equivalentes de definir la función exponencial , una de ellas es

${\displaystyle \exp(x)=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}.}$

Se tiene y la identidad exponencial también se cumple, ya que ${\displaystyle \exp(0)=1,}$ ${\displaystyle \exp(x+y)=\exp(x)\exp(y)}$

${\displaystyle \exp(x)\exp(y)=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}\left(1+{\frac {y}{n}}\right)^{n}=\lim _{n\rightarrow \infty }\left(1+{\frac {x+y}{n}}+{\frac {xy}{n^{2}}}\right)^{n},}$

y el término de segundo orden no afecta el límite, dando como resultado . ${\displaystyle {\frac {xy}{n^{2}}}}$ ${\displaystyle \exp(x)\exp(y)=\exp(x+y)}$

El número de Euler se puede definir como . De las ecuaciones anteriores se deduce que cuando x es un entero (esto resulta de la definición de multiplicación repetida de la exponenciación). Si x es real, resulta de las definiciones dadas en las secciones anteriores, utilizando la identidad exponencial si x es racional y la continuidad de la función exponencial en caso contrario. ${\displaystyle e=\exp(1)}$ ${\displaystyle \exp(x)=e^{x}}$ ${\displaystyle \exp(x)=e^{x}}$

El límite que define la función exponencial converge para cada valor complejo de x y, por lo tanto, se puede utilizar para extender la definición de y, por lo tanto, de los números reales a cualquier argumento complejo z . Esta función exponencial extendida aún satisface la identidad exponencial y se utiliza comúnmente para definir la exponenciación para bases y exponentes complejos. ${\displaystyle \exp(z)}$ ${\displaystyle e^{z},}$

Potencias mediante logaritmos

La definición de e ^x como función exponencial permite definir b ^x para cada número real positivo b , en términos de función exponencial y logarítmica . En concreto, el hecho de que el logaritmo natural ln( x ) sea la inversa de la función exponencial e ^x significa que se tiene

${\displaystyle b=\exp(\ln b)=e^{\ln b}}$

para cada b > 0. Para preservar la identidad se debe tener ${\displaystyle (e^{x})^{y}=e^{xy},}$

${\displaystyle b^{x}=\left(e^{\ln b}\right)^{x}=e^{x\ln b}}$

Por lo tanto, se puede utilizar como definición alternativa de b ^x para cualquier número real positivo b . Esto concuerda con la definición dada anteriormente utilizando exponentes racionales y continuidad, con la ventaja de extenderse directamente a cualquier exponente complejo. ${\displaystyle e^{x\ln b}}$

Exponentes complejos con base real positiva

Si b es un número real positivo, la exponenciación con base b y exponente complejo z se define por medio de la función exponencial con argumento complejo (ver el final del § Función exponencial , arriba) como

${\displaystyle b^{z}=e^{(z\ln b)},}$

donde denota el logaritmo natural de b . ${\displaystyle \ln b}$

Esto satisface la identidad

${\displaystyle b^{z+t}=b^{z}b^{t},}$

En general, no está definida, ya que b ^z no es un número real. Si se le da un significado a la exponenciación de un número complejo (ver § Potencias no enteras de números complejos , más adelante), se tiene, en general, ${\textstyle \left(b^{z}\right)^{t}}$

${\displaystyle \left(b^{z}\right)^{t}\neq b^{zt},}$

a menos que z sea real o t sea un entero.

Fórmula de Euler ,

${\displaystyle e^{iy}=\cos y+i\sin y,}$

permite expresar la forma polar de en términos de las partes reales e imaginarias de z , es decir ${\displaystyle b^{z}}$

${\displaystyle b^{x+iy}=b^{x}(\cos(y\ln b)+i\sin(y\ln b)),}$

donde el valor absoluto del factor trigonométrico es uno. Esto resulta de

${\displaystyle b^{x+iy}=b^{x}b^{iy}=b^{x}e^{iy\ln b}=b^{x}(\cos(y\ln b)+i\sin(y\ln b)).}$

Potencias no enteras de números complejos

En las secciones anteriores, la exponenciación con exponentes no enteros se ha definido sólo para bases reales positivas. Para otras bases, las dificultades aparecen ya con el caso aparentemente simple de raíces n -ésimas, es decir, de exponentes donde n es un entero positivo. Aunque la teoría general de la exponenciación con exponentes no enteros se aplica a raíces n- ésimas , este caso merece ser considerado primero, ya que no necesita utilizar logaritmos complejos y, por lo tanto, es más fácil de entender. ${\displaystyle 1/n,}$

norteraíces de un número complejo

Todo número complejo z distinto de cero puede escribirse en forma polar como

${\displaystyle z=\rho e^{i\theta }=\rho (\cos \theta +i\sin \theta ),}$

donde es el valor absoluto de z , y es su argumento . El argumento se define hasta un múltiplo entero de 2 π ; esto significa que, si es el argumento de un número complejo, entonces es también un argumento del mismo número complejo para cada entero . ${\displaystyle \rho }$ ${\displaystyle \theta }$ ${\displaystyle \theta }$ ${\displaystyle \theta +2k\pi }$ ${\displaystyle k}$

La forma polar del producto de dos números complejos se obtiene multiplicando los valores absolutos y sumando los argumentos. De ello se deduce que la forma polar de una raíz n -ésima de un número complejo se puede obtener tomando la raíz n -ésima del valor absoluto y dividiendo su argumento por n :

${\displaystyle \left(\rho e^{i\theta }\right)^{\frac {1}{n}}={\sqrt[{n}]{\rho }}\,e^{\frac {i\theta }{n}}.}$

Si se suma a , el número complejo no cambia, pero esto se suma al argumento de la raíz n -ésima y proporciona una nueva raíz n -ésima. Esto se puede hacer n veces y proporciona las raíces n - ésimas del número complejo. ${\displaystyle 2\pi }$ ${\displaystyle \theta }$ ${\displaystyle 2i\pi /n}$

Es habitual elegir una de las raíces n n -ésimas como raíz principal . La elección común es elegir la raíz n -ésima para la cual es decir, la raíz n -ésima que tiene la parte real más grande y, si hay dos, la que tiene la parte imaginaria positiva. Esto hace que la raíz n -ésima principal sea una función continua en todo el plano complejo, excepto para valores reales negativos del radicando . Esta función es igual a la raíz n -ésima habitual para radicandos reales positivos. Para radicandos reales negativos y exponentes impares, la raíz n -ésima principal no es real, aunque la raíz n -ésima habitual sí lo es. La continuación analítica muestra que la raíz n -ésima principal es la única función compleja diferenciable que extiende la raíz n -ésima habitual al plano complejo sin los números reales no positivos. ${\displaystyle -\pi <\theta \leq \pi ,}$

Si el número complejo se mueve alrededor del cero incrementando su argumento, tras un incremento de , el número complejo vuelve a su posición inicial, y sus raíces n -ésimas se permutan circularmente (se multiplican por ). Esto demuestra que no es posible definir una función raíz n- ésima que sea continua en todo el plano complejo. ${\displaystyle 2\pi ,}$ $e^{2i\pi /n}$

Raíces de la unidad

Las tres raíces terceras de 1

Las raíces n- ésimas de la unidad son los n números complejos tales que w ⁿ = 1 , donde n es un entero positivo. Surgen en diversas áreas de las matemáticas, como en la transformada de Fourier discreta o en las soluciones algebraicas de ecuaciones algebraicas ( resolvente de Lagrange ).

Las raíces n n ésimas de la unidad son las n primeras potencias de , es decir Las raíces n ésimas de la unidad que tienen esta propiedad generadora se llaman raíces n ésimas primitivas de la unidad ; tienen la forma con k coprimo con n . La única raíz cuadrada primitiva de la unidad es las raíces cuartas primitivas de la unidad son y ${\displaystyle \omega =e^{\frac {2\pi i}{n}}}$ ${\displaystyle 1=\omega ^{0}=\omega ^{n},\omega =\omega ^{1},\omega ^{2},\omega ^{n-1}.}$ ${\displaystyle \omega ^{k}=e^{\frac {2k\pi i}{n}},}$ ${\displaystyle -1;}$ ${\displaystyle i}$ ${\displaystyle -i.}$

Las n -ésimas raíces de la unidad permiten expresar todas las n -ésimas raíces de un número complejo z como los n productos de una n -ésima raíz dada de z con una n -ésima raíz de la unidad.

Geométricamente, las raíces n -ésimas de la unidad se encuentran en el círculo unitario del plano complejo en los vértices de un n -gono regular con un vértice en el número real 1.

Como el número es la raíz n- ésima primitiva de la unidad con el argumento positivo más pequeño , se le llama raíz n- ésima primitiva principal de la unidad , a veces abreviada como raíz n- ésima principal de la unidad , aunque esta terminología puede confundirse con el valor principal de , que es 1. ^{[29] [30] [31]} ${\displaystyle e^{\frac {2k\pi i}{n}}}$ ${\displaystyle 1^{1/n}}$

Exponenciación compleja

La definición de exponenciación con bases complejas conduce a dificultades similares a las descritas en la sección anterior, excepto que, en general, hay infinitos valores posibles para . Por lo tanto, o bien se define un valor principal , que no es continuo para los valores de z que son reales y no positivos, o bien se define como una función multivaluada . $z^{w}$ $z^{w}$

En todos los casos, el logaritmo complejo se utiliza para definir la exponenciación compleja como

${\displaystyle z^{w}=e^{w\log z},}$

donde es la variante del logaritmo complejo que se utiliza, es decir, una función o una función multivaluada tal que ${\displaystyle \log z}$

${\displaystyle e^{\log z}=z}$

para cada z en su dominio de definición .

Valor principal

El valor principal del logaritmo complejo es la única función continua, comúnmente denotada de manera que, para cada número complejo distinto de cero z , ${\displaystyle \log ,}$

${\displaystyle e^{\log z}=z,}$

y el argumento de z satisface

${\displaystyle -\pi <\operatorname {Arg} z\leq \pi .}$

El valor principal del logaritmo complejo no está definido porque es discontinuo en valores reales negativos de z y es holomorfo (es decir, complejo diferenciable) en cualquier otro lugar. Si z es real y positivo, el valor principal del logaritmo complejo es el logaritmo natural: ${\displaystyle z=0,}$ ${\displaystyle \log z=\ln z.}$

El valor principal de se define como donde es el valor principal del logaritmo. ${\displaystyle z^{w}}$ ${\displaystyle z^{w}=e^{w\log z},}$ ${\displaystyle \log z}$

La función es holomorfa excepto en la vecindad de los puntos donde z es real y no positivo. ${\displaystyle (z,w)\to z^{w}}$

Si z es real y positivo, el valor principal de es igual a su valor habitual definido anteriormente. Si donde n es un entero, este valor principal es el mismo que el definido anteriormente. ${\displaystyle z^{w}}$ ${\displaystyle w=1/n,}$

Función multivalor

En algunos contextos, existe un problema con la discontinuidad de los valores principales de y en los valores reales negativos de z . En este caso, es útil considerar estas funciones como funciones multivaluadas . ${\displaystyle \log z}$ ${\displaystyle z^{w}}$

Si denota uno de los valores del logaritmo multivaluado (normalmente su valor principal), los demás valores son donde k es cualquier entero. De manera similar, si es un valor de la potenciación, entonces los demás valores están dados por ${\displaystyle \log z}$ ${\displaystyle 2ik\pi +\log z,}$ ${\displaystyle z^{w}}$

${\displaystyle e^{w(2ik\pi +\log z)}=z^{w}e^{2ik\pi w},}$

donde k es cualquier entero.

Diferentes valores de k dan diferentes valores de a menos que w sea un número racional , es decir, existe un entero d tal que dw es un entero. Esto resulta de la periodicidad de la función exponencial, más específicamente, que si y solo si es un múltiplo entero de ${\displaystyle z^{w}}$ ${\displaystyle e^{a}=e^{b}}$ ${\displaystyle a-b}$ ${\displaystyle 2\pi i.}$

Si es un número racional con m y n enteros coprimos con entonces tiene exactamente n valores. En el caso de que estos valores sean los mismos que los descritos en § Raíces n-ésimas de un número complejo. Si w es un entero, solo hay un valor que concuerda con el de § Exponentes enteros. ${\displaystyle w={\frac {m}{n}}}$ ${\displaystyle n>0,}$ ${\displaystyle z^{w}}$ ${\displaystyle m=1,}$

La exponenciación multivaluada es holomorfa en el sentido de que su gráfica consta de varias láminas que definen cada una una función holomorfa en la vecindad de cada punto. Si z varía continuamente a lo largo de un círculo alrededor de 0 , entonces, después de un giro, el valor de ha cambiado de lámina. ${\displaystyle z\neq 0,}$ ${\displaystyle z^{w}}$

Cálculo

La forma canónica de se puede calcular a partir de la forma canónica de z y w . Aunque esto se puede describir con una única fórmula, resulta más claro dividir el cálculo en varios pasos. ${\displaystyle x+iy}$ ${\displaystyle z^{w}}$

• Forma polar de z . Sies la forma canónica de z ( a y b son reales), entonces su forma polar esdondey(consulte atan2 para la definición de esta función). ${\displaystyle z=a+ib}$ $${\displaystyle z=\rho e^{i\theta }=\rho (\cos \theta +i\sin \theta ),}$$ ${\displaystyle \rho ={\sqrt {a^{2}+b^{2}}}}$ ${\displaystyle \theta =\operatorname {atan2} (a,b)}$
• Logaritmo de z . El valor principal de este logaritmo esdondedenota el logaritmo natural . Los demás valores del logaritmo se obtienen sumandopara cualquier entero k . ${\displaystyle \log z=\ln \rho +i\theta ,}$ ${\displaystyle \ln }$ ${\displaystyle 2ik\pi }$
• Forma canónica de ${\displaystyle w\log z.}$ Si con c y d reales, los valores de son el valor principal correspondiente a ${\displaystyle w=c+di}$ ${\displaystyle w\log z}$ $${\displaystyle w\log z=(c\ln \rho -d\theta -2dk\pi )+i(d\ln \rho +c\theta +2ck\pi ),}$$ ${\displaystyle k=0.}$
• Resultado final . Utilizando las identidades y se obtiene con para el valor principal. ${\displaystyle e^{x+y}=e^{x}e^{y}}$ ${\displaystyle e^{y\ln x}=x^{y},}$ $${\displaystyle z^{w}=\rho ^{c}e^{-d(\theta +2k\pi )}\left(\cos(d\ln \rho +c\theta +2ck\pi )+i\sin(d\ln \rho +c\theta +2ck\pi )\right),}$$ ${\displaystyle k=0}$

Ejemplos

• ${\displaystyle i^{i}}$
  La forma polar de i es y los valores de son, por lo tanto, se deduce que Entonces, todos los valores de son reales, siendo el principal ${\displaystyle i=e^{i\pi /2},}$ ${\displaystyle \log i}$ $${\displaystyle \log i=i\left({\frac {\pi }{2}}+2k\pi \right).}$$ $${\displaystyle i^{i}=e^{i\log i}=e^{-{\frac {\pi }{2}}}e^{-2k\pi }.}$$ ${\displaystyle i^{i}}$ $${\displaystyle e^{-{\frac {\pi }{2}}}\approx 0.2079.}$$
• ${\displaystyle (-2)^{3+4i}}$
  De manera similar, la forma polar de −2 es Entonces, el método descrito anteriormente proporciona los valores En este caso, todos los valores tienen el mismo argumento y diferentes valores absolutos. ${\displaystyle -2=2e^{i\pi }.}$ $${\displaystyle {\begin{aligned}(-2)^{3+4i}&=2^{3}e^{-4(\pi +2k\pi )}(\cos(4\ln 2+3(\pi +2k\pi ))+i\sin(4\ln 2+3(\pi +2k\pi )))\\&=-2^{3}e^{-4(\pi +2k\pi )}(\cos(4\ln 2)+i\sin(4\ln 2)).\end{aligned}}}$$ ${\displaystyle 4\ln 2,}$

En ambos ejemplos, todos los valores de tienen el mismo argumento. En términos más generales, esto es cierto si y solo si la parte real de w es un número entero. ${\displaystyle z^{w}}$

Falla de identidades de potencia y logaritmo

Algunas identidades para potencias y logaritmos de números reales positivos fallarán para números complejos, sin importar cuán complejas sean las potencias y logaritmos complejos definidos como funciones de un solo valor . Por ejemplo:

• La identidad log( b ^x ) = x ⋅ log  b se cumple siempre que b sea un número real positivo y x sea un número real. Pero para la rama principal del logaritmo complejo se tiene

  $${\displaystyle \log((-i)^{2})=\log(-1)=i\pi \neq 2\log(-i)=2\log(e^{-i\pi /2})=2\,{\frac {-i\pi }{2}}=-i\pi }$$

  Independientemente de la rama del logaritmo que se utilice, se producirá un fallo similar en la identidad. Lo mejor que se puede decir (si solo se utiliza este resultado) es que: $${\displaystyle \log w^{z}\equiv z\log w{\pmod {2\pi i}}}$$

  Esta identidad no se cumple ni siquiera cuando se considera log como una función multivaluada. Los valores posibles de log( w ^z ) contienen los de z ⋅ log  w como subconjunto propio . Si utilizamos Log( w ) como valor principal de log( w ) y m , n como números enteros cualesquiera, los valores posibles de ambos lados son:

  $${\displaystyle {\begin{aligned}\left\{\log w^{z}\right\}&=\left\{z\cdot \operatorname {Log} w+z\cdot 2\pi in+2\pi im\mid m,n\in \mathbb {Z} \right\}\\\left\{z\log w\right\}&=\left\{z\operatorname {Log} w+z\cdot 2\pi in\mid n\in \mathbb {Z} \right\}\end{aligned}}}$$
• Las identidades ( bc ) ^x = b ^x c ^x y ( b / c ) ^x = b ^x / c ^x son válidas cuando b y c son números reales positivos y x es un número real. Pero, para los valores principales, se tiene y Por otro lado, cuando x es un entero, las identidades son válidas para todos los números complejos distintos de cero. Si la exponenciación se considera como una función multivaluada, entonces los valores posibles de (−1 ⋅ −1) ^1/2 son {1, −1} . La identidad se cumple, pero decir {1} = {(−1 ⋅ −1) ^1/2 } es incorrecto. $${\displaystyle (-1\cdot -1)^{\frac {1}{2}}=1\neq (-1)^{\frac {1}{2}}(-1)^{\frac {1}{2}}=-1}$$ $${\displaystyle \left({\frac {1}{-1}}\right)^{\frac {1}{2}}=(-1)^{\frac {1}{2}}=i\neq {\frac {1^{\frac {1}{2}}}{(-1)^{\frac {1}{2}}}}={\frac {1}{i}}=-i}$$
• La identidad ( e ^x ) ^y = e ^xy se cumple para los números reales x e y , pero suponer su verdad para números complejos conduce a la siguiente paradoja , descubierta en 1827 por Clausen : ^[32] Para cualquier entero n , tenemos:
  1. ${\displaystyle e^{1+2\pi in}=e^{1}e^{2\pi in}=e\cdot 1=e}$
  2. ${\displaystyle \left(e^{1+2\pi in}\right)^{1+2\pi in}=e\qquad }$(tomando la -ésima potencia de ambos lados) ${\displaystyle (1+2\pi in)}$
  3. ${\displaystyle e^{1+4\pi in-4\pi ^{2}n^{2}}=e\qquad }$(usando y expandiendo el exponente) ${\displaystyle \left(e^{x}\right)^{y}=e^{xy}}$
  4. ${\displaystyle e^{1}e^{4\pi in}e^{-4\pi ^{2}n^{2}}=e\qquad }$(usando ) ${\displaystyle e^{x+y}=e^{x}e^{y}}$
  5. ${\displaystyle e^{-4\pi ^{2}n^{2}}=1\qquad }$(dividiendo por e )
  pero esto es falso cuando el entero n es distinto de cero. El error es el siguiente: por definición, es una notación para una función verdadera, y es una notación para la cual es una función multivaluada. Por lo tanto, la notación es ambigua cuando x = e . Aquí, antes de expandir el exponente, la segunda línea debería ser Por lo tanto, al expandir el exponente, uno ha supuesto implícitamente que para valores complejos de z , lo cual es incorrecto, ya que el logaritmo complejo es multivaluado. En otras palabras, la identidad incorrecta ( e ^x ) ^y = e ^xy debe reemplazarse por la identidad que es una identidad verdadera entre funciones multivaluadas. ${\displaystyle e^{y}}$ ${\displaystyle \exp(y),}$ ${\displaystyle x^{y}}$ ${\displaystyle \exp(y\log x),}$ $${\displaystyle \exp \left((1+2\pi in)\log \exp(1+2\pi in)\right)=\exp(1+2\pi in).}$$ ${\displaystyle \log \exp z=z}$ $${\displaystyle \left(e^{x}\right)^{y}=e^{y\log e^{x}},}$$

Irracionalidad y trascendencia

Si b es un número algebraico real positivo y x es un número racional, entonces b ^x es un número algebraico. Esto resulta de la teoría de extensiones algebraicas . Esto sigue siendo cierto si b es cualquier número algebraico, en cuyo caso, todos los valores de b ^x (como una función multivaluada ) son algebraicos. Si x es irracional (es decir, no racional ), y tanto b como x son algebraicos, el teorema de Gelfond-Schneider afirma que todos los valores de b ^x son trascendentales (es decir, no algebraicos), excepto si b es igual a 0 o 1 .

En otras palabras, si x es irracional y entonces al menos uno de b , x y b ^x es trascendental. ${\displaystyle b\not \in \{0,1\},}$

Potencias enteras en álgebra

La definición de exponenciación con exponentes enteros positivos como multiplicación repetida puede aplicarse a cualquier operación asociativa denotada como una multiplicación. ^{[nb 2]} La definición de x ⁰ requiere además la existencia de una identidad multiplicativa . ^[33]

Una estructura algebraica que consiste en un conjunto junto con una operación asociativa denotada multiplicativamente y una identidad multiplicativa denotada por 1 es un monoide . En tal monoide, la exponenciación de un elemento x se define inductivamente por

• ${\displaystyle x^{0}=1,}$
• ${\displaystyle x^{n+1}=xx^{n}}$para cada entero no negativo n .

Si n es un entero negativo, se define solo si x tiene un inverso multiplicativo . ^[34] En este caso, el inverso de x se denota x ⁻¹ , y x ⁿ se define como ${\displaystyle x^{n}}$ ${\displaystyle \left(x^{-1}\right)^{-n}.}$

La exponenciación con exponentes enteros obedece las siguientes leyes, para x e y en la estructura algebraica, y m y n números enteros:

${\displaystyle {\begin{aligned}x^{0}&=1\\x^{m+n}&=x^{m}x^{n}\\(x^{m})^{n}&=x^{mn}\\(xy)^{n}&=x^{n}y^{n}\quad {\text{if }}xy=yx,{\text{and, in particular, if the multiplication is commutative.}}\end{aligned}}}$

Estas definiciones se utilizan ampliamente en muchas áreas de las matemáticas, en particular para grupos , anillos , cuerpos y matrices cuadradas (que forman un anillo). También se aplican a funciones de un conjunto a sí mismo, que forman un monoide bajo composición de funciones . Esto incluye, como casos específicos, las transformaciones geométricas y los endomorfismos de cualquier estructura matemática .

Cuando existen varias operaciones que pueden repetirse, es común indicar la operación repetida colocando su símbolo en el superíndice, antes del exponente. Por ejemplo, si f es una función real cuyo valor puede ser multiplicado, denota la potenciación respecto de la multiplicación, y puede denotar la potenciación respecto de la composición de la función . Es decir, ${\displaystyle f^{n}}$ ${\displaystyle f^{\circ n}}$

${\displaystyle (f^{n})(x)=(f(x))^{n}=f(x)\,f(x)\cdots f(x),}$

y

${\displaystyle (f^{\circ n})(x)=f(f(\cdots f(f(x))\cdots )).}$

Comúnmente, se denota mientras que se denota ${\displaystyle (f^{n})(x)}$ ${\displaystyle f(x)^{n},}$ ${\displaystyle (f^{\circ n})(x)}$ ${\displaystyle f^{n}(x).}$

En un grupo

Un grupo multiplicativo es un conjunto con una operación asociativa denotada como multiplicación, que tiene un elemento identidad y tal que cada elemento tiene un inverso.

Entonces, si G es un grupo, se define para todo y cada entero n . ${\displaystyle x^{n}}$ ${\displaystyle x\in G}$

El conjunto de todas las potencias de un elemento de un grupo forma un subgrupo . Un grupo (o subgrupo) que consta de todas las potencias de un elemento específico x es el grupo cíclico generado por x . Si todas las potencias de x son distintas, el grupo es isomorfo al grupo aditivo de los números enteros. En caso contrario, el grupo cíclico es finito (tiene un número finito de elementos), y su número de elementos es el orden de x . Si el orden de x es n , entonces y el grupo cíclico generado por x consta de las n primeras potencias de x (empezando indistintamente por el exponente 0 o 1 ). ${\displaystyle \mathbb {Z} }$ ${\displaystyle x^{n}=x^{0}=1,}$

El orden de los elementos juega un papel fundamental en la teoría de grupos . Por ejemplo, el orden de un elemento en un grupo finito es siempre un divisor del número de elementos del grupo (el orden del grupo). Los posibles órdenes de los elementos del grupo son importantes en el estudio de la estructura de un grupo (ver teoremas de Sylow ) y en la clasificación de grupos finitos simples .

La notación superíndice también se utiliza para la conjugación ; es decir, g ^h = h ⁻¹ gh , donde g y h son elementos de un grupo. Esta notación no se puede confundir con la exponenciación, ya que el superíndice no es un número entero. La motivación de esta notación es que la conjugación obedece algunas de las leyes de la exponenciación, a saber : ${\displaystyle (g^{h})^{k}=g^{hk}}$ ${\displaystyle (gh)^{k}=g^{k}h^{k}.}$

En un anillo

En un anillo , puede ocurrir que algunos elementos distintos de cero satisfagan para algún entero n . Se dice que un elemento de este tipo es nilpotente . En un anillo conmutativo , los elementos nilpotentes forman un ideal , llamado radical nil del anillo. ${\displaystyle x^{n}=0}$

Si el radical nil se reduce al ideal cero (es decir, si implica para cada entero positivo n ), se dice que el anillo conmutativo está reducido . Los anillos reducidos son importantes en geometría algebraica , ya que el anillo de coordenadas de un conjunto algebraico afín es siempre un anillo reducido. ${\displaystyle x\neq 0}$ ${\displaystyle x^{n}\neq 0}$

En términos más generales, dado un ideal I en un anillo conmutativo R , el conjunto de los elementos de R que tienen una potencia en I es un ideal, llamado radical de I . El nilradical es el radical del ideal cero . Un ideal radical es un ideal que es igual a su propio radical. En un anillo de polinomios sobre un cuerpo k , un ideal es radical si y solo si es el conjunto de todos los polinomios que son cero en un conjunto algebraico afín (esto es una consecuencia del Nullstellensatz de Hilbert ). ${\displaystyle k[x_{1},\ldots ,x_{n}]}$

Matrices y operadores lineales

Si A es una matriz cuadrada, entonces el producto de A consigo misma n veces se denomina potencia de matriz . También se define como la matriz identidad, ^[35] y si A es invertible, entonces . ${\displaystyle A^{0}}$ ${\displaystyle A^{-n}=\left(A^{-1}\right)^{n}}$

Las potencias matriciales aparecen a menudo en el contexto de sistemas dinámicos discretos , donde la matriz A expresa una transición desde un vector de estado x de algún sistema al siguiente estado Ax del sistema. ^[36] Esta es la interpretación estándar de una cadena de Markov , por ejemplo. Entonces es el estado del sistema después de dos pasos de tiempo, y así sucesivamente: es el estado del sistema después de n pasos de tiempo. La potencia matricial es la matriz de transición entre el estado actual y el estado en un momento n pasos en el futuro. Por lo tanto, calcular potencias matriciales es equivalente a resolver la evolución del sistema dinámico. En muchos casos, las potencias matriciales se pueden calcular convenientemente utilizando valores propios y vectores propios . ${\displaystyle A^{2}x}$ ${\displaystyle A^{n}x}$ ${\displaystyle A^{n}}$

Además de las matrices, también se pueden exponenciar operadores lineales más generales. Un ejemplo es el operador de derivada del cálculo, , que es un operador lineal que actúa sobre funciones para dar una nueva función . La potencia n del operador de diferenciación es la derivada n : ${\displaystyle d/dx}$ ${\displaystyle f(x)}$ ${\displaystyle (d/dx)f(x)=f'(x)}$

${\displaystyle \left({\frac {d}{dx}}\right)^{n}f(x)={\frac {d^{n}}{dx^{n}}}f(x)=f^{(n)}(x).}$

Estos ejemplos son para exponentes discretos de operadores lineales, pero en muchas circunstancias también es deseable definir potencias de tales operadores con exponentes continuos. Este es el punto de partida de la teoría matemática de semigrupos . ^[37] Así como el cálculo de potencias matriciales con exponentes discretos resuelve sistemas dinámicos discretos, el cálculo de potencias matriciales con exponentes continuos resuelve sistemas con dinámica continua. Los ejemplos incluyen enfoques para resolver la ecuación del calor , la ecuación de Schrödinger , la ecuación de onda y otras ecuaciones diferenciales parciales que incluyen una evolución temporal. El caso especial de exponenciar el operador derivada a una potencia no entera se llama derivada fraccionaria que, junto con la integral fraccionaria , es una de las operaciones básicas del cálculo fraccionario .

Campos finitos

Un campo es una estructura algebraica en la que se definen la multiplicación, la suma, la resta y la división y satisfacen las propiedades de que la multiplicación es asociativa y cada elemento distinto de cero tiene un inverso multiplicativo . Esto implica que la exponenciación con exponentes enteros está bien definida, excepto para potencias no positivas de 0. Ejemplos comunes son el campo de números complejos , los números reales y los números racionales , considerados anteriormente en este artículo, que son todos infinitos .

Un cuerpo finito es un cuerpo con un número finito de elementos. Este número de elementos es un número primo o una potencia prima ; es decir, tiene la forma donde p es un número primo y k es un entero positivo. Para cada uno de estos q , existen cuerpos con q elementos. Los cuerpos con q elementos son todos isomorfos , lo que permite, en general, trabajar como si hubiera un solo cuerpo con q elementos, denotado ${\displaystyle q=p^{k},}$ ${\displaystyle \mathbb {F} _{q}.}$

Uno tiene

${\displaystyle x^{q}=x}$

Para cada uno ${\displaystyle x\in \mathbb {F} _{q}.}$

Un elemento primitivo en es un elemento g tal que el conjunto de las q − 1 primeras potencias de g (es decir, ) es igual al conjunto de los elementos distintos de cero de Hay elementos primitivos en donde es la función totiente de Euler . ${\displaystyle \mathbb {F} _{q}}$ ${\displaystyle \{g^{1}=g,g^{2},\ldots ,g^{p-1}=g^{0}=1\}}$ ${\displaystyle \mathbb {F} _{q}.}$ ${\displaystyle \varphi (p-1)}$ ${\displaystyle \mathbb {F} _{q},}$ ${\displaystyle \varphi }$

En la identidad soñada del estudiante de primer año ${\displaystyle \mathbb {F} _{q},}$

${\displaystyle (x+y)^{p}=x^{p}+y^{p}}$

es cierto para el exponente p . Como en Se deduce que el mapa ${\displaystyle x^{p}=x}$ ${\displaystyle \mathbb {F} _{q},}$

${\displaystyle {\begin{aligned}F\colon {}&\mathbb {F} _{q}\to \mathbb {F} _{q}\\&x\mapsto x^{p}\end{aligned}}}$

es lineal sobre y es un automorfismo de cuerpo , llamado automorfismo de Frobenius . Si el cuerpo tiene k automorfismos, que son las k primeras potencias (bajo composición ) de F . En otras palabras, el grupo de Galois de es cíclico de orden k , generado por el automorfismo de Frobenius. ${\displaystyle \mathbb {F} _{q},}$ ${\displaystyle q=p^{k},}$ ${\displaystyle \mathbb {F} _{q}}$ ${\displaystyle \mathbb {F} _{q}}$

The Diffie–Hellman key exchange is an application of exponentiation in finite fields that is widely used for secure communications. It uses the fact that exponentiation is computationally inexpensive, whereas the inverse operation, the discrete logarithm, is computationally expensive. More precisely, if g is a primitive element in ${\displaystyle \mathbb {F} _{q},}$ then ${\displaystyle g^{e}}$ can be efficiently computed with exponentiation by squaring for any e, even if q is large, while there is no known computationally practical algorithm that allows retrieving e from ${\displaystyle g^{e}}$ if q is sufficiently large.

Powers of sets

The Cartesian product of two sets S and T is the set of the ordered pairs ${\displaystyle (x,y)}$ such that ${\displaystyle x\in S}$ and ${\displaystyle y\in T.}$ This operation is not properly commutative nor associative, but has these properties up to canonical isomorphisms, that allow identifying, for example, ${\displaystyle (x,(y,z)),}$ ${\displaystyle ((x,y),z),}$ and ${\displaystyle (x,y,z).}$

This allows defining the nth power ${\displaystyle S^{n}}$ of a set S as the set of all n-tuples ${\displaystyle (x_{1},\ldots ,x_{n})}$ of elements of S.

When S is endowed with some structure, it is frequent that ${\displaystyle S^{n}}$ is naturally endowed with a similar structure. In this case, the term "direct product" is generally used instead of "Cartesian product", and exponentiation denotes product structure. For example ${\displaystyle \mathbb {R} ^{n}}$ (where ${\displaystyle \mathbb {R} }$ denotes the real numbers) denotes the Cartesian product of n copies of ${\displaystyle \mathbb {R} ,}$ as well as their direct product as vector space, topological spaces, rings, etc.

Sets as exponents

A n-tuple ${\displaystyle (x_{1},\ldots ,x_{n})}$ of elements of S can be considered as a function from ${\displaystyle \{1,\ldots ,n\}.}$ This generalizes to the following notation.

Given two sets S and T, the set of all functions from T to S is denoted ${\displaystyle S^{T}}$. This exponential notation is justified by the following canonical isomorphisms (for the first one, see Currying):

${\displaystyle (S^{T})^{U}\cong S^{T\times U},}$

${\displaystyle S^{T\sqcup U}\cong S^{T}\times S^{U},}$

where ${\displaystyle \times }$ denotes the Cartesian product, and ${\displaystyle \sqcup }$ the disjoint union.

One can use sets as exponents for other operations on sets, typically for direct sums of abelian groups, vector spaces, or modules. For distinguishing direct sums from direct products, the exponent of a direct sum is placed between parentheses. For example, ${\displaystyle \mathbb {R} ^{\mathbb {N} }}$ denotes the vector space of the infinite sequences of real numbers, and ${\displaystyle \mathbb {R} ^{(\mathbb {N} )}}$ the vector space of those sequences that have a finite number of nonzero elements. The latter has a basis consisting of the sequences with exactly one nonzero element that equals 1, while the Hamel bases of the former cannot be explicitly described (because their existence involves Zorn's lemma).

In this context, 2 can represents the set ${\displaystyle \{0,1\}.}$ So, ${\displaystyle 2^{S}}$ denotes the power set of S, that is the set of the functions from S to ${\displaystyle \{0,1\},}$ which can be identified with the set of the subsets of S, by mapping each function to the inverse image of 1.

This fits in with the exponentiation of cardinal numbers, in the sense that |S^T| = |S|^|T|, where |X| is the cardinality of X.

In category theory

In the category of sets, the morphisms between sets X and Y are the functions from X to Y. It results that the set of the functions from X to Y that is denoted ${\displaystyle Y^{X}}$ in the preceding section can also be denoted ${\displaystyle \hom(X,Y).}$ The isomorphism ${\displaystyle (S^{T})^{U}\cong S^{T\times U}}$ can be rewritten

${\displaystyle \hom(U,S^{T})\cong \hom(T\times U,S).}$

This means the functor "exponentiation to the power T " is a right adjoint to the functor "direct product with T ".

This generalizes to the definition of exponentiation in a category in which finite direct products exist: in such a category, the functor ${\displaystyle X\to X^{T}}$ is, if it exists, a right adjoint to the functor ${\displaystyle Y\to T\times Y.}$ A category is called a Cartesian closed category, if direct products exist, and the functor ${\displaystyle Y\to X\times Y}$ has a right adjoint for every T.

Repeated exponentiation

Just as exponentiation of natural numbers is motivated by repeated multiplication, it is possible to define an operation based on repeated exponentiation; this operation is sometimes called hyper-4 or tetration. Iterating tetration leads to another operation, and so on, a concept named hyperoperation. This sequence of operations is expressed by the Ackermann function and Knuth's up-arrow notation. Just as exponentiation grows faster than multiplication, which is faster-growing than addition, tetration is faster-growing than exponentiation. Evaluated at (3, 3), the functions addition, multiplication, exponentiation, and tetration yield 6, 9, 27, and 7625597484987 (=3²⁷ = 3³³ = ³3) respectively.

Limits of powers

Zero to the power of zero gives a number of examples of limits that are of the indeterminate form 0⁰. The limits in these examples exist, but have different values, showing that the two-variable function x^y has no limit at the point (0, 0). One may consider at what points this function does have a limit.

More precisely, consider the function ${\displaystyle f(x,y)=x^{y}}$ defined on ${\displaystyle D=\{(x,y)\in \mathbf {R} ^{2}:x>0\}}$. Then D can be viewed as a subset of R² (that is, the set of all pairs (x, y) with x, y belonging to the extended real number line R = [−∞, +∞], endowed with the product topology), which will contain the points at which the function f has a limit.

In fact, f has a limit at all accumulation points of D, except for (0, 0), (+∞, 0), (1, +∞) and (1, −∞).^[38] Accordingly, this allows one to define the powers x^y by continuity whenever 0 ≤ x ≤ +∞, −∞ ≤ y ≤ +∞, except for 0⁰, (+∞)⁰, 1^+∞ and 1^−∞, which remain indeterminate forms.

Under this definition by continuity, we obtain:

• x^+∞ = +∞ and x^−∞ = 0, when 1 < x ≤ +∞.
• x^+∞ = 0 and x^−∞ = +∞, when 0 ≤ x < 1.
• 0^y = 0 and (+∞)^y = +∞, when 0 < y ≤ +∞.
• 0^y = +∞ and (+∞)^y = 0, when −∞ ≤ y < 0.

These powers are obtained by taking limits of x^y for positive values of x. This method does not permit a definition of x^y when x < 0, since pairs (x, y) with x < 0 are not accumulation points of D.

On the other hand, when n is an integer, the power xⁿ is already meaningful for all values of x, including negative ones. This may make the definition 0ⁿ = +∞ obtained above for negative n problematic when n is odd, since in this case xⁿ → +∞ as x tends to 0 through positive values, but not negative ones.

Efficient computation with integer exponents

Computing bⁿ using iterated multiplication requires n − 1 multiplication operations, but it can be computed more efficiently than that, as illustrated by the following example. To compute 2¹⁰⁰, apply Horner's rule to the exponent 100 written in binary:

${\displaystyle 100=2^{2}+2^{5}+2^{6}=2^{2}(1+2^{3}(1+2))}$.

Then compute the following terms in order, reading Horner's rule from right to left.

This series of steps only requires 8 multiplications instead of 99.

In general, the number of multiplication operations required to compute bⁿ can be reduced to ${\displaystyle \sharp n+\lfloor \log _{2}n\rfloor -1,}$ by using exponentiation by squaring, where ${\displaystyle \sharp n}$ denotes the number of 1s in the binary representation of n. For some exponents (100 is not among them), the number of multiplications can be further reduced by computing and using the minimal addition-chain exponentiation. Finding the minimal sequence of multiplications (the minimal-length addition chain for the exponent) for bⁿ is a difficult problem, for which no efficient algorithms are currently known (see Subset sum problem), but many reasonably efficient heuristic algorithms are available.^[39] However, in practical computations, exponentiation by squaring is efficient enough, and much more easy to implement.

Iterated functions

Function composition is a binary operation that is defined on functions such that the codomain of the function written on the right is included in the domain of the function written on the left. It is denoted ${\displaystyle g\circ f,}$ and defined as

${\displaystyle (g\circ f)(x)=g(f(x))}$

for every x in the domain of f.

If the domain of a function f equals its codomain, one may compose the function with itself an arbitrary number of time, and this defines the nth power of the function under composition, commonly called the nth iterate of the function. Thus ${\displaystyle f^{n}}$ denotes generally the nth iterate of f; for example, ${\displaystyle f^{3}(x)}$ means ${\displaystyle f(f(f(x))).}$^[40]

When a multiplication is defined on the codomain of the function, this defines a multiplication on functions, the pointwise multiplication, which induces another exponentiation. When using functional notation, the two kinds of exponentiation are generally distinguished by placing the exponent of the functional iteration before the parentheses enclosing the arguments of the function, and placing the exponent of pointwise multiplication after the parentheses. Thus ${\displaystyle f^{2}(x)=f(f(x)),}$ and ${\displaystyle f(x)^{2}=f(x)\cdot f(x).}$ When functional notation is not used, disambiguation is often done by placing the composition symbol before the exponent; for example ${\displaystyle f^{\circ 3}=f\circ f\circ f,}$ and ${\displaystyle f^{3}=f\cdot f\cdot f.}$ For historical reasons, the exponent of a repeated multiplication is placed before the argument for some specific functions, typically the trigonometric functions. So, ${\displaystyle \sin ^{2}x}$ and ${\displaystyle \sin ^{2}(x)}$ both mean ${\displaystyle \sin(x)\cdot \sin(x)}$ and not ${\displaystyle \sin(\sin(x)),}$ which, in any case, is rarely considered. Historically, several variants of these notations were used by different authors.^[41][42][43]

In this context, the exponent ${\displaystyle -1}$ denotes always the inverse function, if it exists. So ${\displaystyle \sin ^{-1}x=\sin ^{-1}(x)=\arcsin x.}$ For the multiplicative inverse fractions are generally used as in ${\displaystyle 1/\sin(x)={\frac {1}{\sin x}}.}$

In programming languages

Programming languages generally express exponentiation either as an infix operator or as a function application, as they do not support superscripts. The most common operator symbol for exponentiation is the caret (^). The original version of ASCII included an uparrow symbol (↑), intended for exponentiation, but this was replaced by the caret in 1967, so the caret became usual in programming languages.^[44]The notations include:

• x ^ y: AWK, BASIC, J, MATLAB, Wolfram Language (Mathematica), R, Microsoft Excel, Analytica, TeX (and its derivatives), TI-BASIC, bc (for integer exponents), Haskell (for nonnegative integer exponents), Lua, and most computer algebra systems.
• x ** y. The Fortran character set did not include lowercase characters or punctuation symbols other than +-*/()&=.,' and so used ** for exponentiation^[45][46] (the initial version used a xx b instead.^[47]). Many other languages followed suit: Ada, Z shell, KornShell, Bash, COBOL, CoffeeScript, Fortran, FoxPro, Gnuplot, Groovy, JavaScript, OCaml, F#, Perl, PHP, PL/I, Python, Rexx, Ruby, SAS, Seed7, Tcl, ABAP, Mercury, Haskell (for floating-point exponents), Turing, and VHDL.
• x ↑ y: Algol Reference language, Commodore BASIC, TRS-80 Level II/III BASIC.^[48][49]
• x ^^ y: Haskell (for fractional base, integer exponents), D.
• x⋆y: APL.

In most programming languages with an infix exponentiation operator, it is right-associative, that is, a^b^c is interpreted as a^(b^c).^[50] This is because (a^b)^c is equal to a^(b*c) and thus not as useful. In some languages, it is left-associative, notably in Algol, MATLAB, and the Microsoft Excel formula language.

Other programming languages use functional notation:

• (expt x y): Common Lisp.
• pown x y: F# (for integer base, integer exponent).

Still others only provide exponentiation as part of standard libraries:

• pow(x, y): C, C++ (in math library).
• Math.Pow(x, y): C#.
• math:pow(X, Y): Erlang.
• Math.pow(x, y): Java.
• [Math]::Pow(x, y): PowerShell.

In some statically typed languages that prioritize type safety such as Rust, exponentiation is performed via a multitude of methods:

• x.pow(y) for x and y as integers
• x.powf(y) for x and y as floating point numbers
• x.powi(y) for x as a float and y as an integer

See also

• Mathematics portal

• Double exponential function
• Exponential decay
• Exponential field
• Exponential growth
• Hyperoperation
• Tetration
• Pentation
• List of exponential topics
• Modular exponentiation
• Scientific notation
• Unicode subscripts and superscripts
• x^y = y^x
• Zero to the power of zero

Notes

1. There are three common notations for multiplication: ${\displaystyle x\times y}$ is most commonly used for explicit numbers and at a very elementary level; ${\displaystyle xy}$ is most common when variables are used; ${\displaystyle x\cdot y}$ is used for emphasizing that one talks of multiplication or when omitting the multiplication sign would be confusing.
2. More generally, power associativity is sufficient for the definition.

References

1. Nykamp, Duane. "Basic rules for exponentiation". Math Insight. Retrieved 2020-08-27.
2. Weisstein, Eric W. "Power". MathWorld. Retrieved 2020-08-27.
3. "Exponent | Etymology of exponent by etymonline".
4. Rotman, Joseph J. (2015). Advanced Modern Algebra, Part 1. Graduate Studies in Mathematics. Vol. 165 (3rd ed.). Providence, RI: American Mathematical Society. p. 130, fn. 4. ISBN 978-1-4704-1554-9.
5. Szabó, Árpád (1978). The Beginnings of Greek Mathematics. Synthese Historical Library. Vol. 17. Translated by A.M. Ungar. Dordrecht: D. Reidel. p. 37. ISBN 90-277-0819-3.
6. O'Connor, John J.; Robertson, Edmund F. "Etymology of some common mathematical terms". MacTutor History of Mathematics Archive. University of St Andrews.
7. Ball, W. W. Rouse (1915). A Short Account of the History of Mathematics (6th ed.). London: Macmillan. p. 38.
8. Archimedes. (2009). THE SAND-RECKONER. In T. Heath (Ed.), The Works of Archimedes: Edited in Modern Notation with Introductory Chapters (Cambridge Library Collection - Mathematics, pp. 229-232). Cambridge: Cambridge University Press. doi:10.1017/CBO9780511695124.017.
9. Quinion, Michael. "Zenzizenzizenzic". World Wide Words. Retrieved 2020-04-16.
10. O'Connor, John J.; Robertson, Edmund F. "Abu'l Hasan ibn Ali al Qalasadi". MacTutor History of Mathematics Archive. University of St Andrews.
11. Cajori, Florian (1928). A History of Mathematical Notations. Vol. 1. The Open Court Company. p. 102.
12. Cajori, Florian (1928). A History of Mathematical Notations. Vol. 1. London: Open Court Publishing Company. p. 344.
13. "Earliest Known Uses of Some of the Words of Mathematics (E)". 2017-06-23.
14. Stifel, Michael (1544). Arithmetica integra. Nuremberg: Johannes Petreius. p. 235v.
15. Cajori, Florian (1928). A History of Mathematical Notations. Vol. 1. The Open Court Company. p. 204.
16. Descartes, René (1637). "La Géométrie". Discourse de la méthode [...]. Leiden: Jan Maire. p. 299. Et aa, ou a², pour multiplier a par soy mesme; Et a³, pour le multiplier encore une fois par a, & ainsi a l'infini (And aa, or a², in order to multiply a by itself; and a³, in order to multiply it once more by a, and thus to infinity).
17. The most recent usage in this sense cited by the OED is from 1806 ("involution". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)).
18. Euler, Leonhard (1748). Introductio in analysin infinitorum (in Latin). Vol. I. Lausanne: Marc-Michel Bousquet. pp. 69, 98–99. Primum ergo considerandæ sunt quantitates exponentiales, seu Potestates, quarum Exponens ipse est quantitas variabilis. Perspicuum enim est hujusmodi quantitates ad Functiones algebraicas referri non posse, cum in his Exponentes non nisi constantes locum habeant.
19. Hodge, Jonathan K.; Schlicker, Steven; Sundstorm, Ted (2014). Abstract Algebra: an inquiry based approach. CRC Press. p. 94. ISBN 978-1-4665-6706-1.
20. Achatz, Thomas (2005). Technical Shop Mathematics (3rd ed.). Industrial Press. p. 101. ISBN 978-0-8311-3086-2.
21. Knobloch, Eberhard (1994). "The infinite in Leibniz's mathematics – The historiographical method of comprehension in context". In Kostas Gavroglu; Jean Christianidis; Efthymios Nicolaidis (eds.). Trends in the Historiography of Science. Boston Studies in the Philosophy of Science. Vol. 151. Springer Netherlands. p. 276. doi:10.1007/978-94-017-3596-4_20. ISBN 9789401735964. A positive power of zero is infinitely small, a negative power of zero is infinite.
22. Bronstein, Ilja Nikolaevič; Semendjajew, Konstantin Adolfovič (1987) [1945]. "2.4.1.1. Definition arithmetischer Ausdrücke" [Definition of arithmetic expressions]. Written at Leipzig, Germany. In Grosche, Günter; Ziegler, Viktor; Ziegler, Dorothea (eds.). Taschenbuch der Mathematik [Pocketbook of mathematics] (in German). Vol. 1. Translated by Ziegler, Viktor. Weiß, Jürgen (23 ed.). Thun, Switzerland / Frankfurt am Main, Germany: Verlag Harri Deutsch (and B. G. Teubner Verlagsgesellschaft, Leipzig). pp. 115–120, 802. ISBN 3-87144-492-8.
23. Olver, Frank W. J.; Lozier, Daniel W.; Boisvert, Ronald F.; Clark, Charles W., eds. (2010). NIST Handbook of Mathematical Functions. National Institute of Standards and Technology (NIST), U.S. Department of Commerce, Cambridge University Press. ISBN 978-0-521-19225-5. MR 2723248.[1]
24. Zeidler, Eberhard [in German]; Schwarz, Hans Rudolf; Hackbusch, Wolfgang; Luderer, Bernd [in German]; Blath, Jochen; Schied, Alexander; Dempe, Stephan; Wanka, Gert; Hromkovič, Juraj; Gottwald, Siegfried (2013) [2012]. Zeidler, Eberhard [in German] (ed.). Springer-Handbuch der Mathematik I (in German). Vol. I (1 ed.). Berlin / Heidelberg, Germany: Springer Spektrum, Springer Fachmedien Wiesbaden. p. 590. ISBN 978-3-658-00284-8. (xii+635 pages)
25. Hass, Joel R.; Heil, Christopher E.; Weir, Maurice D.; Thomas, George B. (2018). Thomas' Calculus (14 ed.). Pearson. pp. 7–8. ISBN 9780134439020.
26. Anton, Howard; Bivens, Irl; Davis, Stephen (2012). Calculus: Early Transcendentals (9th ed.). John Wiley & Sons. p. 28. ISBN 9780470647691.
27. Denlinger, Charles G. (2011). Elements of Real Analysis. Jones and Bartlett. pp. 278–283. ISBN 978-0-7637-7947-4.
28. Tao, Terence (2016). "Limits of sequences". Analysis I. Texts and Readings in Mathematics. Vol. 37. pp. 126–154. doi:10.1007/978-981-10-1789-6_6. ISBN 978-981-10-1789-6.
29. Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). Introduction to Algorithms (second ed.). MIT Press. ISBN 978-0-262-03293-3. Online resource Archived 2007-09-30 at the Wayback Machine.
30. Cull, Paul; Flahive, Mary; Robson, Robby (2005). Difference Equations: From Rabbits to Chaos (Undergraduate Texts in Mathematics ed.). Springer. ISBN 978-0-387-23234-8. Defined on p. 351.
31. Weisstein, Eric W. "Principal root of unity". MathWorld.
32. Steiner, J.; Clausen, T.; Abel, Niels Henrik (1827). "Aufgaben und Lehrsätze, erstere aufzulösen, letztere zu beweisen" [Problems and propositions, the former to solve, the later to prove]. Journal für die reine und angewandte Mathematik. 2: 286–287.
33. Bourbaki, Nicolas (1970). Algèbre. Springer. I.2.
34. Bloom, David M. (1979). Linear Algebra and Geometry. Cambridge University Press. p. 45. ISBN 978-0-521-29324-2.
35. Chapter 1, Elementary Linear Algebra, 8E, Howard Anton.
36. Strang, Gilbert (1988). Linear algebra and its applications (3rd ed.). Brooks-Cole. Chapter 5.
37. E. Hille, R. S. Phillips: Functional Analysis and Semi-Groups. American Mathematical Society, 1975.
38. Nicolas Bourbaki, Topologie générale, V.4.2.
39. Gordon, D. M. (1998). "A Survey of Fast Exponentiation Methods" (PDF). Journal of Algorithms. 27: 129–146. CiteSeerX 10.1.1.17.7076. doi:10.1006/jagm.1997.0913. Archived from the original (PDF) on 2018-07-23. Retrieved 2024-01-11.
40. Peano, Giuseppe (1903). Formulaire mathématique (in French). Vol. IV. p. 229.
41. Herschel, John Frederick William (1813) [1812-11-12]. "On a Remarkable Application of Cotes's Theorem". Philosophical Transactions of the Royal Society of London. 103 (Part 1). London: Royal Society of London, printed by W. Bulmer and Co., Cleveland-Row, St. James's, sold by G. and W. Nicol, Pall-Mall: 8–26 [10]. doi:10.1098/rstl.1813.0005. JSTOR 107384. S2CID 118124706.
42. Herschel, John Frederick William (1820). "Part III. Section I. Examples of the Direct Method of Differences". A Collection of Examples of the Applications of the Calculus of Finite Differences. Cambridge, UK: Printed by J. Smith, sold by J. Deighton & sons. pp. 1–13 [5–6]. Archived from the original on 2020-08-04. Retrieved 2020-08-04. [2] (NB. Inhere, Herschel refers to his 1813 work and mentions Hans Heinrich Bürmann's older work.)
43. Cajori, Florian (1952) [March 1929]. A History of Mathematical Notations. Vol. 2 (3rd ed.). Chicago, USA: Open court publishing company. pp. 108, 176–179, 336, 346. ISBN 978-1-60206-714-1. Retrieved 2016-01-18.
44. Richard Gillam (2003). Unicode Demystified: A Practical Programmer's Guide to the Encoding Standard. Addison-Wesley Professional. p. 33. ISBN 0201700522.
45. Backus, John Warner; Beeber, R. J.; Best, Sheldon F.; Goldberg, Richard; Herrick, Harlan L.; Hughes, R. A.; Mitchell, L. B.; Nelson, Robert A.; Nutt, Roy; Sayre, David; Sheridan, Peter B.; Stern, Harold; Ziller, Irving (1956-10-15). Sayre, David (ed.). The FORTRAN Automatic Coding System for the IBM 704 EDPM: Programmer's Reference Manual (PDF). New York, USA: Applied Science Division and Programming Research Department, International Business Machines Corporation. p. 15. Archived (PDF) from the original on 2022-07-04. Retrieved 2022-07-04. (2+51+1 pages)
46. Brice Carnahan; James O. Wilkes (1968). Introduction to Digital Computing and FORTRAN IV with MTS Applications. pp. 2–2, 2–6.
47. Backus, John Warner; Herrick, Harlan L.; Nelson, Robert A.; Ziller, Irving (1954-11-10). Backus, John Warner (ed.). Specifications for: The IBM Mathematical FORmula TRANSlating System, FORTRAN (PDF) (Preliminary report). New York, USA: Programming Research Group, Applied Science Division, International Business Machines Corporation. pp. 4, 6. Archived (PDF) from the original on 2022-03-29. Retrieved 2022-07-04. (29 pages)
48. Daneliuk, Timothy "Tim" A. (1982-08-09). "BASCOM - A BASIC compiler for TRS-80 I and II". InfoWorld. Software Reviews. Vol. 4, no. 31. Popular Computing, Inc. pp. 41–42. Archived from the original on 2020-02-07. Retrieved 2020-02-06.
49. "80 Contents". 80 Micro (45). 1001001, Inc.: 5. October 1983. ISSN 0744-7868. Retrieved 2020-02-06.
50. Robert W. Sebesta (2010). Concepts of Programming Languages. Addison-Wesley. pp. 130, 324. ISBN 978-0136073475.