Base (álgebra lineal)

Conjunto de vectores utilizados para definir coordenadas.

Un mismo vector se puede representar en dos bases diferentes (flechas moradas y rojas).

En matemáticas , un conjunto B de vectores en un espacio vectorial V se llama base ( pl.: bases ) si cada elemento de V puede escribirse de forma única como una combinación lineal finita de elementos de B. Los coeficientes de esta combinación lineal se denominan componentes o coordenadas del vector con respecto a B. Los elementos de una base se llamanvectores de base .

De manera equivalente, un conjunto B es una base si sus elementos son linealmente independientes y cada elemento de V es una combinación lineal de elementos de B. ^[1] En otras palabras, una base es un conjunto generador linealmente independiente .

Un espacio vectorial puede tener varias bases; sin embargo todas las bases tienen la misma cantidad de elementos, llamada dimensión del espacio vectorial .

Este artículo trata principalmente de espacios vectoriales de dimensión finita. Sin embargo, muchos de los principios también son válidos para espacios vectoriales de dimensión infinita.

Definición

Una base B de un espacio vectorial V sobre un campo F ( como los números reales R o los números complejos C ) es un subconjunto linealmente independiente de V que abarca V. Esto significa que un subconjunto B de V es una base si satisface las dos condiciones siguientes:

independencia lineal

para cada subconjunto finito de B , si es para alguno en F , entonces ; ${\displaystyle \{\mathbf {v} _{1},\dotsc ,\mathbf {v} _{m}\}}$ ${\displaystyle c_{1}\mathbf {v} _{1}+\cdots +c_{m}\mathbf {v} _{m}=\mathbf {0} }$ ${\displaystyle c_{1},\dotsc ,c_{m}}$ ${\displaystyle c_{1}=\cdots =c_{m}=0}$

propiedad que abarca

para cada vector v en V , se puede elegir en F y en B tal que . ${\displaystyle a_{1},\dotsc ,a_{n}}$ ${\displaystyle \mathbf {v} _{1},\dotsc ,\mathbf {v} _{n}}$ ${\displaystyle \mathbf {v} =a_{1}\mathbf {v} _{1}+\cdots +a_{n}\mathbf {v} _{n}}$

Los escalares se denominan coordenadas del vector v con respecto a la base B y por la primera propiedad están determinadas de forma única. ${\displaystyle a_{i}}$

Un espacio vectorial que tiene una base finita se llama de dimensión finita . En este caso, el subconjunto finito se puede tomar como el propio B para verificar la independencia lineal en la definición anterior.

A menudo es conveniente o incluso necesario tener un orden en los vectores base, por ejemplo, cuando se habla de orientación , o cuando se consideran los coeficientes escalares de un vector con respecto a una base sin hacer referencia explícita a los elementos de la base. En este caso, el ordenamiento es necesario para asociar cada coeficiente al elemento base correspondiente. Este orden se puede realizar numerando los elementos básicos. Para enfatizar que se ha elegido un orden, se habla de base ordenada , que por tanto no es simplemente un conjunto no estructurado , sino una secuencia , una familia indexada , o similar; ver § Bases ordenadas y coordenadas a continuación.

Ejemplos

Esta imagen ilustra la base estándar en R ² . Los vectores azul y naranja son los elementos de la base; el vector verde se puede dar en términos de los vectores base y, por tanto, depende linealmente de ellos.

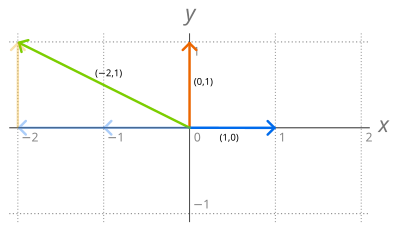
El conjunto R ² de los pares ordenados de números reales es un espacio vectorial bajo las operaciones de suma por componentes

$${\displaystyle (a,b)+(c,d)=(a+c,b+d)}$$

$${\displaystyle \lambda (a,b)=(\lambda a,\lambda b),}$$

e ₁ = (1, 0)e ₂ = (0, 1)base estándarv = ( a , b )R ² ${\displaystyle \lambda }$

$${\displaystyle \mathbf {v} =a\mathbf {e} _{1}+b\mathbf {e} _{2}.}$$

R ²(1, 1)(−1, 2)R ²

De manera más general, si F es un campo , el conjunto de n -tuplas de elementos de F es un espacio vectorial para suma y multiplicación escalar definidas de manera similar. Dejar ${\displaystyle F^{n}}$

$${\displaystyle \mathbf {e} _{i}=(0,\ldots ,0,1,0,\ldots ,0)}$$

nibase estándar ${\displaystyle \mathbf {e} _{1},\ldots ,\mathbf {e} _{n}}$ ${\displaystyle F^{n},}$ ${\displaystyle F^{n}.}$

Un ejemplo diferente lo dan los anillos polinomiales . Si F es un campo, la colección F [ X ] de todos los polinomios en un X indeterminado con coeficientes en F es un espacio vectorial F. Una base para este espacio es la base monomial B , que consta de todos los monomios :

$${\displaystyle B=\{1,X,X^{2},\ldots \}.}$$

polinomios de base de Bernsteinlos polinomios de Chebyshevsecuencia polinómicaF [ X ]

Propiedades

Muchas propiedades de las bases finitas resultan del lema de intercambio de Steinitz , que establece que, para cualquier espacio vectorial V , dado un conjunto finito S y un conjunto linealmente independiente L de n elementos de V , se pueden reemplazar n elementos bien elegidos de S. por los elementos de L para obtener un conjunto generador que contenga L , que tenga sus otros elementos en S y que tenga el mismo número de elementos que S .

La mayoría de las propiedades resultantes del lema de intercambio de Steinitz siguen siendo verdaderas cuando no hay un conjunto finito, pero sus demostraciones en el caso infinito generalmente requieren el axioma de elección o una forma más débil del mismo, como el lema del ultrafiltro .

Si V es un espacio vectorial sobre un campo F , entonces:

• Si L es un subconjunto linealmente independiente de un conjunto generador S ⊆ V , entonces existe una base B tal que
  $${\displaystyle L\subseteq B\subseteq S.}$$
• V tiene una base (esta es la propiedad anterior, siendo L el conjunto vacío y S = V ).
• Todas las bases de V tienen la misma cardinalidad , lo que se denomina dimensión de V. Este es el teorema de la dimensión .
• Un conjunto generador S es una base de V si y sólo si es mínimo, es decir, ningún subconjunto propio de S es también un conjunto generador de V.
• Un conjunto linealmente independiente L es una base si y sólo si es máximo, es decir, no es un subconjunto propio de ningún conjunto linealmente independiente.

Si V es un espacio vectorial de dimensión n , entonces:

• Un subconjunto de V con n elementos es una base si y sólo si es linealmente independiente.
• Un subconjunto de V con n elementos es una base si y sólo si es un conjunto generador de V.

Coordenadas

Sea V un espacio vectorial de dimensión finita n sobre un campo F , y

$${\displaystyle B=\{\mathbf {b} _{1},\ldots ,\mathbf {b} _{n}\}}$$

VvV

$${\displaystyle \mathbf {v} =\lambda _{1}\mathbf {b} _{1}+\cdots +\lambda _{n}\mathbf {b} _{n},}$$

)coordenadasvB. conjuntoconjunto{2, 3}forma ordenadaindexandosecuenciamarco ${\displaystyle \lambda _{1},\ldots ,\lambda _{n}}$ ${\displaystyle 3\mathbf {b} _{1}+2\mathbf {b} _{2}}$ ${\displaystyle 2\mathbf {b} _{1}+3\mathbf {b} _{2}}$

Sea, como siempre, el conjunto de las n -tuplas de elementos de F . Este conjunto es un F -espacio vectorial, con la suma y la multiplicación escalar definidas por componentes. El mapa ${\displaystyle F^{n}}$

$${\displaystyle \varphi :(\lambda _{1},\ldots ,\lambda _{n})\mapsto \lambda _{1}\mathbf {b} _{1}+\cdots +\lambda _{n}\mathbf {b} _{n}}$$

isomorfismo linealVespacio de coordenadasVnvector de coordenadasv ${\displaystyle F^{n}}$ ${\displaystyle F^{n}}$ ${\displaystyle \varphi ^{-1}(\mathbf {v} )}$

La imagen inversa de es la n -tupla cuyos componentes son 0, excepto el i -ésimo que es 1. La forma es una base ordenada de , que se llama base estándar o base canónica . La base ordenada B es la imagen de la base canónica de . ${\displaystyle \varphi }$ ${\displaystyle \mathbf {b} _{i}}$ ${\displaystyle \mathbf {e} _{i}}$ ${\displaystyle \mathbf {e} _{i}}$ ${\displaystyle F^{n}}$ ${\displaystyle \varphi }$ ${\displaystyle F^{n}}$

De lo anterior se deduce que cada base ordenada es la imagen mediante un isomorfismo lineal de la base canónica de , y que cada isomorfismo lineal de sobre V puede definirse como el isomorfismo que mapea la base canónica de sobre una base ordenada dada de V . En otras palabras, equivale a definir una base ordenada de V , o un isomorfismo lineal de sobre V. ${\displaystyle F^{n}}$ ${\displaystyle F^{n}}$ ${\displaystyle F^{n}}$ ${\displaystyle F^{n}}$

Cambio de base

Sea V un espacio vectorial de dimensión n sobre un campo F. Dadas dos bases (ordenadas) y de V , a menudo es útil expresar las coordenadas de un vector x con respecto a en términos de las coordenadas con respecto a Esto se puede hacer mediante la fórmula de cambio de base , que se describe a continuación . Se han elegido los subíndices "antiguo" y "nuevo" porque es habitual referirse a y como base antigua y base nueva , respectivamente. Es útil describir las coordenadas antiguas en términos de las nuevas, porque, en general, se tienen expresiones que involucran las coordenadas antiguas, y si se quiere obtener expresiones equivalentes en términos de las coordenadas nuevas; esto se obtiene reemplazando las antiguas coordenadas por sus expresiones en términos de las nuevas coordenadas. ${\displaystyle B_{\text{old}}=(\mathbf {v} _{1},\ldots ,\mathbf {v} _{n})}$ ${\displaystyle B_{\text{new}}=(\mathbf {w} _{1},\ldots ,\mathbf {w} _{n})}$ ${\displaystyle B_{\mathrm {old} }}$ ${\displaystyle B_{\mathrm {new} }.}$ ${\displaystyle B_{\mathrm {old} }}$ ${\displaystyle B_{\mathrm {new} }}$

Normalmente, los nuevos vectores de base están dados por sus coordenadas sobre la base anterior, es decir,

$${\displaystyle \mathbf {w} _{j}=\sum _{i=1}^{n}a_{i,j}\mathbf {v} _{i}.}$$

x ${\displaystyle (x_{1},\ldots ,x_{n})}$ ${\displaystyle (y_{1},\ldots ,y_{n})}$

$${\displaystyle x_{i}=\sum _{j=1}^{n}a_{i,j}y_{j},}$$

i = 1, ..., norte

Esta fórmula se puede escribir de forma concisa en notación matricial . Sea A la matriz de , y ${\displaystyle a_{i,j}}$

$${\displaystyle X={\begin{bmatrix}x_{1}\\\vdots \\x_{n}\end{bmatrix}}\quad {\text{and}}\quad Y={\begin{bmatrix}y_{1}\\\vdots \\y_{n}\end{bmatrix}}}$$

vectores columnav

$${\displaystyle X=AY.}$$

La fórmula se puede probar considerando la descomposición del vector x en las dos bases: se tiene

$${\displaystyle \mathbf {x} =\sum _{i=1}^{n}x_{i}\mathbf {v} _{i},}$$

$${\displaystyle \mathbf {x} =\sum _{j=1}^{n}y_{j}\mathbf {w} _{j}=\sum _{j=1}^{n}y_{j}\sum _{i=1}^{n}a_{i,j}\mathbf {v} _{i}=\sum _{i=1}^{n}{\biggl (}\sum _{j=1}^{n}a_{i,j}y_{j}{\biggr )}\mathbf {v} _{i}.}$$

La fórmula del cambio de base resulta entonces de la unicidad de la descomposición de un vector sobre una base, aquí ; eso es ${\displaystyle B_{\text{old}}}$

$${\displaystyle x_{i}=\sum _{j=1}^{n}a_{i,j}y_{j},}$$

i = 1, ..., norte

Nociones relacionadas

módulo gratuito

Si se reemplaza el campo que aparece en la definición de un espacio vectorial por un anillo , se obtiene la definición de un módulo . Para los módulos, la independencia lineal y los conjuntos de expansión se definen exactamente como para los espacios vectoriales, aunque " conjunto generador " se usa más comúnmente que "conjunto de expansión".

Al igual que en los espacios vectoriales, la base de un módulo es un subconjunto linealmente independiente que también es un conjunto generador. Una diferencia importante con la teoría de los espacios vectoriales es que no todos los módulos tienen una base. Un módulo que tiene una base se llama módulo libre . Los módulos libres juegan un papel fundamental en la teoría de módulos, ya que pueden usarse para describir la estructura de módulos no libres a través de resoluciones libres .

Un módulo sobre los números enteros es exactamente lo mismo que un grupo abeliano . Por tanto, un módulo libre sobre los números enteros también es un grupo abeliano libre. Los grupos abelianos libres tienen propiedades específicas que los módulos no comparten con otros anillos. Específicamente, cada subgrupo de un grupo abeliano libre es un grupo abeliano libre y, si G es un subgrupo de un grupo abeliano libre finitamente generado H (es decir, un grupo abeliano que tiene una base finita), entonces hay una base de H y un número entero 0 ≤ k ≤ n tal que sea una base de G , para algunos números enteros distintos de cero . Para obtener más información, consulte Grupo abeliano libre § Subgrupos . ${\displaystyle \mathbf {e} _{1},\ldots ,\mathbf {e} _{n}}$ ${\displaystyle a_{1}\mathbf {e} _{1},\ldots ,a_{k}\mathbf {e} _{k}}$ ${\displaystyle a_{1},\ldots ,a_{k}}$

Análisis

En el contexto de espacios vectoriales de dimensión infinita sobre números reales o complejos, el términoLa base de Hamel (llamada así porGeorg Hamel^[2]) ola base algebraicase pueden utilizar para referirse a una base como se define en este artículo. Esto es para hacer una distinción con otras nociones de "base" que existen cuando los espacios vectoriales de dimensión infinita están dotados de una estructura adicional. Las alternativas más importantes sonlas bases ortogonalesenespacios de Hilbert,las bases de Schauderylas bases de Markushevichenespacios lineales normados. En el caso de los números realesRvistos como un espacio vectorial sobre el campoQde los números racionales, las bases de Hamel son incontables, y tienen específicamente lacardinalidaddel continuo, que es elnúmero cardinal ,donde(alef-nada) es el más pequeño cardinal infinito, el cardinal de los números enteros. ${\displaystyle 2^{\aleph _{0}}}$ ${\displaystyle \aleph _{0}}$

La característica común de las otras nociones es que permiten tomar infinitas combinaciones lineales de los vectores base para generar el espacio. Esto, por supuesto, requiere que se definan significativamente sumas infinitas en estos espacios, como es el caso de los espacios vectoriales topológicos , una gran clase de espacios vectoriales que incluyen, por ejemplo, espacios de Hilbert , espacios de Banach o espacios de Fréchet .

La preferencia de otros tipos de bases por espacios de dimensión infinita se justifica por el hecho de que la base de Hamel se vuelve "demasiado grande" en los espacios de Banach: si X es un espacio vectorial normado de dimensión infinita que es completo (es decir, X es un espacio de Banach ), entonces cualquier base Hamel de X es necesariamente incontable . Esto es una consecuencia del teorema de la categoría de Baire . La integridad y la dimensión infinita son supuestos cruciales en la afirmación anterior. De hecho, los espacios de dimensión finita tienen, por definición, bases finitas y hay espacios normados de dimensión infinita ( no completos ) que tienen bases de Hamel contables. Considere , el espacio de las secuencias de números reales que tienen sólo un número finito de elementos distintos de cero, con la norma . Su base estándar , que consta de secuencias que tienen un solo elemento distinto de cero, que es igual a 1, es una base de Hamel contable. ${\displaystyle c_{00}}$ ${\displaystyle x=(x_{n})}$ ${\textstyle \|x\|=\sup _{n}|x_{n}|}$

Ejemplo

En el estudio de las series de Fourier , se aprende que las funciones {1} ∪ { sin( nx ), cos( nx ) : n = 1, 2, 3, ... } son una "base ortogonal" de las series (reales o complejo) espacio vectorial de todas las funciones (reales o de valores complejos) en el intervalo [0, 2π] que son integrables al cuadrado en este intervalo, es decir, funciones f que satisfacen

$${\displaystyle \int _{0}^{2\pi }\left|f(x)\right|^{2}\,dx<\infty .}$$

Las funciones {1} ∪ { sin( nx ), cos( nx ) : n = 1, 2, 3, ... } son linealmente independientes, y cada función f que es integrable al cuadrado en [0, 2π] es una "combinación lineal infinita" de ellos, en el sentido de que

$${\displaystyle \lim _{n\to \infty }\int _{0}^{2\pi }{\biggl |}a_{0}+\sum _{k=1}^{n}\left(a_{k}\cos \left(kx\right)+b_{k}\sin \left(kx\right)\right)-f(x){\biggr |}^{2}dx=0}$$

para coeficientes adecuados (reales o complejos) a _k , b _k . Pero muchas ^[3] funciones integrables al cuadrado no pueden representarse como combinaciones lineales finitas de estas funciones base, que por lo tanto no comprenden una base de Hamel. Cada base de Hamel de este espacio es mucho más grande que este conjunto de funciones meramente contablemente infinito. Las bases de Hamel de espacios de este tipo normalmente no son útiles, mientras que las bases ortonormales de estos espacios son esenciales en el análisis de Fourier .

Geometría

Las nociones geométricas de espacio afín , espacio proyectivo , conjunto convexo y cono tienen nociones relacionadas de base . ^[4] Una base afín para un espacio afín de n dimensiones son los puntos en posición lineal general . A ${\displaystyle n+1}$La base proyectiva sonpuntos en posición general, en un espacio proyectivo de dimensiónn. A ${\displaystyle n+2}$La base convexa de unpolitopoes el conjunto de los vértices de sucáscara convexa. ALa base del cono ^[5]consiste en un punto por arista de un cono poligonal. Véase también unabase de Hilbert (programación lineal).

Base aleatoria

Para una distribución de probabilidad en R ⁿ con una función de densidad de probabilidad , como la equidistribución en una bola de n dimensiones con respecto a la medida de Lebesgue, se puede demostrar que n vectores elegidos aleatoria e independientemente formarán una base con probabilidad uno , que es debido al hecho de que n vectores linealmente dependientes x ₁ , ..., x _n en R ⁿ deberían satisfacer la ecuación det[ x ₁ ⋯ x _n ] = 0 (determinante cero de la matriz con columnas x _i ), y el conjunto de ceros de un polinomio no trivial tiene medida cero. Esta observación ha llevado a técnicas para aproximar bases aleatorias. ^{[6] [7]}

Distribución empírica de longitudes N de cadenas de vectores casi ortogonales por pares que se muestrean aleatoriamente de forma independiente del cubo de n dimensiones [−1, 1] ⁿ en función de la dimensión, n . Los diagramas de caja muestran el segundo y tercer cuartil de estos datos para cada n , las barras rojas corresponden a las medianas y las estrellas azules indican las medias. La curva roja muestra el límite teórico dado por la ecuación. (1) y la curva verde muestra una estimación refinada. ^[7]

Es difícil comprobar numéricamente la dependencia lineal o la ortogonalidad exacta. Por tanto, se utiliza la noción de ε-ortogonalidad. Para espacios con producto interno , x es ε-ortogonal a y si (es decir, el coseno del ángulo entre xey es menor que ε ) . ${\displaystyle \left|\left\langle x,y\right\rangle \right|/\left(\left\|x\right\|\left\|y\right\|\right)<\varepsilon }$

En dimensiones altas, dos vectores aleatorios independientes son con alta probabilidad casi ortogonales, y el número de vectores aleatorios independientes, que con una alta probabilidad dada son casi ortogonales por pares, crece exponencialmente con la dimensión. Más precisamente, considere la equidistribución en una bola de n dimensiones. Elija N vectores aleatorios independientes de una bola (son independientes y están distribuidos de manera idéntica ). Sea θ un pequeño número positivo. Entonces para

N vectores aleatorios son todos ε-ortogonales por pares con probabilidad 1 − θ . ^[7] Este N crece exponencialmente con dimensión n y para n suficientemente grande . Esta propiedad de las bases aleatorias es una manifestación del llamado fenómeno de concentración de medidas . ^[8] ${\displaystyle N\gg n}$

La figura (derecha) ilustra la distribución de longitudes N de cadenas de vectores casi ortogonales por pares que se muestrean aleatoriamente de forma independiente del cubo n -dimensional [−1, 1] ⁿ en función de la dimensión, n . Primero se selecciona aleatoriamente un punto en el cubo. El segundo punto se elige al azar en el mismo cubo. Si el ángulo entre los vectores estaba dentro de π/2 ± 0,037π/2, entonces se retuvo el vector. En el siguiente paso se genera un nuevo vector en el mismo hipercubo y se evalúan sus ángulos con los vectores generados previamente. Si estos ángulos están dentro de π/2 ± 0,037π/2, entonces se conserva el vector. El proceso se repite hasta que se rompe la cadena de casi ortogonalidad y se registra el número de dichos vectores casi ortogonales por pares (longitud de la cadena). Para cada n , se construyeron numéricamente 20 cadenas casi ortogonales por pares para cada dimensión. Se presenta la distribución de la longitud de estas cadenas.

Prueba de que todo espacio vectorial tiene una base.

Sea V cualquier espacio vectorial sobre algún campo F. Sea X el conjunto de todos los subconjuntos linealmente independientes de V.

El conjunto X no está vacío ya que el conjunto vacío es un subconjunto independiente de V y está parcialmente ordenado por inclusión, que se denota, como siempre, por ⊆ .

Sea Y un subconjunto de X que está totalmente ordenado por ⊆ , y sea L _Y la unión de todos los elementos de Y (que son en sí mismos ciertos subconjuntos de V ).

Dado que ( Y , ⊆) está totalmente ordenado, cada subconjunto finito de L _Y es un subconjunto de un elemento de Y , que es un subconjunto linealmente independiente de V , y por tanto L _Y es linealmente independiente. Por tanto, L Y _es un elemento de X. Por lo tanto, L _Y es un límite superior para Y en ( X , ⊆) : es un elemento de X , que contiene todos los elementos de Y.

Como X no está vacío y cada subconjunto totalmente ordenado de ( X , ⊆) tiene un límite superior en X , el lema de Zorn afirma que X tiene un elemento máximo. En otras palabras, existe algún elemento L _max de X que satisface la condición de que siempre que L _max ⊆ L para algún elemento L de X , entonces L = L _max .

Queda por demostrar que Lmax es una base _de V. Dado que L _max pertenece a X , ya sabemos que L _max es un subconjunto linealmente independiente de V.

Si hubiera algún vector w de V que no esté en el lapso de L _max , entonces w tampoco sería un elemento de L _max . Sea L _w = L _max ∪ { w } . Este conjunto es un elemento de X , es decir, es un subconjunto linealmente independiente de V (porque w no está en el lapso de L _max y L _max es independiente). Como L _max ⊆ L _w y L _max ≠ L _w (porque L _w contiene el vector w que no está contenido en L _max ), esto contradice la maximalidad de L _max . Por tanto, esto muestra que L _max abarca V .

Por tanto, L _max es linealmente independiente y abarca V . Por tanto, es una base de V , y esto prueba que todo espacio vectorial tiene una base.

Esta prueba se basa en el lema de Zorn, que equivale al axioma de elección . Por el contrario, se ha demostrado que si todo espacio vectorial tiene una base, entonces el axioma de elección es verdadero. ^[9] Por tanto, las dos afirmaciones son equivalentes.

Ver también

• Base de una matroide
• Base de un programa lineal
• Cambio de base  : cambio de coordenadas en álgebra lineal
• Marco de un espacio vectorial  : similar a la base de un espacio vectorial, pero no necesariamente linealmente independiente.Pages displaying short descriptions of redirect targets
• Base esférica  : base utilizada para expresar tensores esféricos.

Notas

1. Halmos, Paul Richard (1987). Espacios vectoriales de dimensiones finitas (4ª ed.). Nueva York: Springer. pag. 10.ISBN​ 978-0-387-90093-3.
2. Hamel 1905
3. Tenga en cuenta que no se puede decir "la mayoría" porque las cardinalidades de los dos conjuntos (funciones que pueden y no pueden representarse con un número finito de funciones básicas) son las mismas.
4. Rees, Elmer G. (2005). Notas sobre geometría. Berlín: Springer. pag. 7.ISBN​ 978-3-540-12053-7.
5. Kuczma, Marek (1970). "Algunas observaciones sobre funciones aditivas en conos". Aecuaciones Mathematicae . 4 (3): 303–306. doi :10.1007/BF01844160. S2CID  189836213.
6. Igelnik, B.; Pao, Y.-H. (1995). "Elección estocástica de funciones base en la aproximación de funciones adaptativas y la red de enlaces funcionales". Traducción IEEE. Red neuronal . 6 (6): 1320-1329. doi : 10.1109/72.471375. PMID  18263425.
7. Gorban, Alexander N .; Tyukin, Ivan Y.; Prokhorov, Danil V.; Sofeikov, Konstantin I. (2016). "Aproximación con bases aleatorias: pro y contra". Ciencias de la Información . 364–365: 129–145. arXiv : 1506.04631 . doi :10.1016/j.ins.2015.09.021. S2CID  2239376.
8. Artstein, Shiri (2002). «Fenómenos de concentración proporcional de la esfera» (PDF) . Revista Israelí de Matemáticas . 132 (1): 337–358. CiteSeerX 10.1.1.417.2375 . doi : 10.1007/BF02784520 . S2CID  8095719. 
9. Blas 1984

Referencias

Referencias generales

• Blass, Andreas (1984), "La existencia de bases implica el axioma de elección" (PDF) , Teoría de conjuntos axiomáticos , Matemáticas contemporáneas volumen 31, Providence, RI: American Mathematical Society , págs. 31–33, ISBN 978-0-8218-5026-8, señor  0763890
• Brown, William A. (1991), Matrices y espacios vectoriales, Nueva York: M. Dekker, ISBN 978-0-8247-8419-5
• Lang, Serge (1987), Álgebra lineal , Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-96412-6

Referencias históricas

• Banach, Stefan (1922), "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (Sobre operaciones en conjuntos abstractos y su aplicación a ecuaciones integrales)" (PDF) , Fundamenta Mathematicae (en francés), 3 : 133– 181, doi :10.4064/fm-3-1-133-181, ISSN  0016-2736
• Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Consideraciones de algunos aspectos de la geometría elemental) (en alemán)
• Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elementos de la historia de las matemáticas) (en francés), París: Hermann
• Dorier, Jean-Luc (1995), "Un esquema general de la génesis de la teoría del espacio vectorial", Historia Mathematica , 22 (3): 227–261, doi : 10.1006/hmat.1995.1024 , MR  1347828
• Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (en francés), Chez Firmin Didot, père et fils
• Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (en alemán), reimpresión: Hermann Grassmann. Traducido por Lloyd C. Kannenberg. (2000), Teoría de la extensión , Kannenberg, LC, Providence, RI: Sociedad Matemática Estadounidense , ISBN 978-0-8218-2031-5
• Hamel, Georg (1905), "Eine Basis aller Zahlen und die unstetigen Lösungen der Funktionalgleichung f(x+y)=f(x)+f(y)", Mathematische Annalen (en alemán), Leipzig, 60 (3): 459–462, doi :10.1007/BF01457624, S2CID  120063569
• Hamilton, William Rowan (1853), Conferencias sobre cuaterniones, Real Academia Irlandesa
• Möbius, August Ferdinand (1827), Der Barycentrische Calcul: ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Cálculo baricéntrico: una nueva utilidad para un tratamiento analítico de la geometría) (en alemán), archivado desde el original el 12 de abril de 2009
• Moore, Gregory H. (1995), "La axiomatización del álgebra lineal: 1875-1940", Historia Mathematica , 22 (3): 262–303, doi : 10.1006/hmat.1995.1025
• Peano, Giuseppe (1888), Calcolo Geométrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva (en italiano), Turín{{citation}}: CS1 maint: location missing publisher (link)

enlaces externos

• Vídeos instructivos de Khan Academy
  • Introducción a las bases de los subespacios.
  • Prueba de que cualquier base subespacial tiene el mismo número de elementos.
• "Combinaciones lineales, tramos y vectores de base". Esencia del álgebra lineal . 6 de agosto de 2016. Archivado desde el original el 17 de noviembre de 2021, a través de YouTube .
• "Base", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]