0,999…
En otras palabras, los símbolos «0,999...» y «1» son dos representaciones distintas del mismo número real.
La igualdad 0,999... = 1 ha sido aceptada desde hace tiempo por los matemáticos y se la incluye en los libros de texto.
La igualdad 0,999... = 1 está íntimamente relacionada con la ausencia de números reales infinitesimales no nulos.
Aunque los números reales son el objeto de estudio más común en el campo del análisis matemático, tanto los hiperreales como los p-ádicos tienen aplicaciones en esta área.
En álgebra elemental, estas demostraciones explican por qué el método general de conversión entre fracciones y números decimales funciona.
[9] Una sucesión (x0, x1, x2, ...) tiene por límite x si la distancia |x − xn| se vuelve arbitrariamente pequeña a medida que n aumenta.
La afirmación misma 0,999... = 1 puede ser interpretada y demostrada como límite:[10] El último paso, que
El proceso opuesto proporciona una visión complementaria: para un número real dado, definir la expansión decimal que lo denota.
Si un número real x pertenece al intervalo cerrado [0 ; 10] (i.e, es mayor o igual a cero y menor o igual a diez), se puede dividir este intervalo en diez partes que se superpongan únicamente en las extremidades: [0 ; 1], [1 ; 2], [2 ; 3], y así hasta [9 ; 10].
Para asegurarse de que esta notación no abuse del signo «=», se requiere de un método que permita reconstruir un único número real para cada decimal, como por ejemplo los límites; otras construcciones abordan el tema del ordenamiento.
Para explotar directamente estos objetos, se define b0,b1b2b3... como la mínima cota superior del conjunto de aproximantes {b0 ; b0,b1 ; b0,b1b2 ; ...}.
Estos conjuntos numéricos se acompañan de las cuatro operaciones aritméticas fundamentales: suma, resta, multiplicación y división.
[...] Entonces vemos que en la definición tradicional de los números reales, la ecuación 0,9* = 1 está incorporada desde el comienzo.
"[22] Una modificación suplementaria del proceso lleva a una estructura diferente en donde no son iguales.
[24] Luego, según este formalismo, la tarea es mostrar que la sucesión de números racionales tiene por límite 0.
El libro está escrito específicamente para ofrecer una segunda mirada sobre conceptos familiares bajo una interpretación moderna.
En general, para casi todo q entre 1 y 2, existen incontables expansiones en q-base del 1.
Este resultado fue obtenido por vez primera por Paul Erdős, Miklos Horváth e István Joó alrededor de 1990.
En esta base, 1 = 0,11010011001011010010110011010011...; los dígitos vienen dados por la sucesión de Thue-Morse, que no se repite.
[34] Los nueves repetidos aparecen también en otro trabajo de George Cantor: deben tomarse en cuenta para construir una prueba válida, al aplicar su prueba diagonal de 1891 a las expansiones decimales ed la no denombrabilidad del intervalo unidad.
Esta demostración necesita poder declarar la diferencia entre ciertos pares de números reales basada en sus expansiones decimales, por lo que se deben evitar parejas como 0,2 y 0,1999... Un método simple representa todos los números con expansión no finita; el método opuesto excluye nueves repetitivos.
Interrogando a sus estudiantes para determinar por qué la vasta mayoría rechaza inicialmente la igualdad, encontró que «los estudiantes continúan concibiendo el 0,999... como una sucesión de números que se acercan más y más a 1 y no como un valor fijo, porque 'no se ha especificado cuántos lugares hay' o 'es el decimal más cercano posible debajo del 1'».
[41] Tampoco están a salvo métodos más sofisticados: estudiantes que son absolutamente capaces de aplicar definiciones rigurosas, pueden aún sentir la necesidad de recurrir a imágenes intuitivas cuando son sorprendidos por resultados matemáticos avanzados, incluyendo 0,999...
[45] Las FAQ abarcan brevemente el caso 1⁄3, multiplicación por 10, límites y también alude a las sucesiones de Cauchy.
Se pueden construir estructuras algebraicas ordenadas, matemáticamente coherentes, incluyendo varias alternativas a los números reales, que son no arquimedianas.
Aunque no discute directamente 0,999..., muestra que el número real 1/3 se representa por 0,333...;...333... como consecuencia del principio de transferencia.
[55][56] La teoría de juegos combinatorios provee números alternativos a los reales; un ejemplo notorio es el Hackenbush[57] azul-negro infinito.
Después de definir la multiplicación, los números decimales forman un semianillo conmutativo positivo, totalmente ordenado.
Se puede sumar un 1 al lugar de las unidades, lo que deja detrás solo 0's después del acarreo: 1 + ...999 = ...000 = 0, y así ...999 = −1.
Esta ecuación no tiene sentido ni como expansión 10-ádica ni como expansión decimal ordinaria, pero resulta ser significativa y verdadera si se desarrolla una teoría de «dobles-decimales» con, eventualmente, terminaciones repetitivas a la izquierda para representar un sistema muy conocido: los números reales.




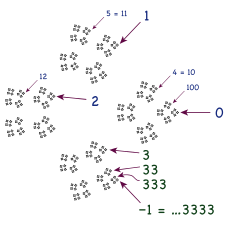
El 10-ádico análogo es ...999 = −1.
