Matriz (matemáticas)

Array of numbers

Una matriz m × n : las m filas son horizontales y las n columnas son verticales. Cada elemento de una matriz suele estar representado por una variable con dos subíndices . Por _ejemplo , 2,1 representa el elemento de la segunda fila y la primera columna de la matriz.

En matemáticas , una matriz ( pl.: matrices ) es una matriz rectangular o tabla de números , símbolos o expresiones , con elementos o entradas dispuestos en filas y columnas, que se utiliza para representar un objeto matemático o una propiedad de dicho objeto.

Por ejemplo, es una matriz con dos filas y tres columnas. A menudo se la denomina "matriz de dos por tres", " matriz" o matriz de dimensión . $${\displaystyle {\begin{bmatrix}1&9&-13\\20&5&-6\end{bmatrix}}}$$ ${\displaystyle 2\times 3}$ ${\displaystyle 2\times 3}$

Las matrices se relacionan comúnmente con el álgebra lineal . Las excepciones notables incluyen las matrices de incidencia y las matrices de adyacencia en la teoría de grafos . ^[1] Este artículo se centra en las matrices relacionadas con el álgebra lineal y, a menos que se especifique lo contrario, todas las matrices representan aplicaciones lineales o pueden considerarse como tales.

Las matrices cuadradas , matrices con el mismo número de filas y columnas, desempeñan un papel importante en la teoría de matrices. Las matrices cuadradas de una dimensión dada forman un anillo no conmutativo , que es uno de los ejemplos más comunes de un anillo no conmutativo. El determinante de una matriz cuadrada es un número asociado con la matriz, que es fundamental para el estudio de una matriz cuadrada; por ejemplo, una matriz cuadrada es invertible si y solo si tiene un determinante distinto de cero y los valores propios de una matriz cuadrada son las raíces de un determinante polinomial .

En geometría , las matrices se utilizan ampliamente para especificar y representar transformaciones geométricas (por ejemplo, rotaciones ) y cambios de coordenadas . En análisis numérico , muchos problemas computacionales se resuelven reduciéndolos a un cálculo matricial, y esto a menudo implica realizar cálculos con matrices de enormes dimensiones. Las matrices se utilizan en la mayoría de las áreas de las matemáticas y los campos científicos, ya sea directamente o mediante su uso en geometría y análisis numérico.

La teoría de matrices es la rama de las matemáticas que se centra en el estudio de las matrices. Inicialmente era una subrama del álgebra lineal , pero pronto se expandió para incluir temas relacionados con la teoría de grafos , el álgebra , la combinatoria y la estadística .

Definición

Una matriz es una matriz rectangular de números (u otros objetos matemáticos), denominadas las entradas de la matriz. Las matrices están sujetas a operaciones estándar como la suma y la multiplicación. ^[2] Lo más común es que una matriz sobre un cuerpo F sea una matriz rectangular de elementos de F. ^{[3] [4]} Una matriz real y una matriz compleja son matrices cuyas entradas son, respectivamente, números reales o números complejos . A continuación se analizan tipos de entradas más generales. Por ejemplo, esta es una matriz real:

${\displaystyle \mathbf {A} ={\begin{bmatrix}-1.3&0.6\\20.4&5.5\\9.7&-6.2\end{bmatrix}}.}$

Los números, símbolos o expresiones de la matriz se denominan sus entradas o sus elementos . Las líneas horizontales y verticales de entradas de una matriz se denominan filas y columnas , respectivamente.

Tamaño

El tamaño de una matriz se define por el número de filas y columnas que contiene. No hay límite para el número de filas y columnas que una matriz (en el sentido habitual) puede tener siempre que sean números enteros positivos. Una matriz con filas y columnas se denomina matriz, o matriz por matriz, donde y se denominan sus dimensiones . Por ejemplo, la matriz anterior es una matriz. ${\displaystyle {m}}$ ${\displaystyle {n}}$ ${\displaystyle {m\times n}}$ ${\displaystyle {m}}$ ${\displaystyle {n}}$ ${\displaystyle {m}}$ ${\displaystyle {n}}$ ${\displaystyle {\mathbf {A} }}$ ${\displaystyle {3\times 2}}$

Las matrices con una sola fila se denominan vectores fila y las que tienen una sola columna se denominan vectores columna . Una matriz con el mismo número de filas y columnas se denomina matriz cuadrada . ^[5] Una matriz con un número infinito de filas o columnas (o ambas) se denomina matriz infinita. En algunos contextos, como en los programas de álgebra computacional , es útil considerar una matriz sin filas o sin columnas, llamada matriz vacía.

Notación

Los detalles de la notación simbólica de matrices varían ampliamente, con algunas tendencias predominantes. Las matrices se escriben comúnmente entre corchetes o paréntesis , de modo que una matriz se representa como Esto se puede abreviar escribiendo solo un término genérico, posiblemente junto con índices, como en o en el caso de que . ${\displaystyle m\times n}$ ${\displaystyle \mathbf {A} }$ $${\displaystyle \mathbf {A} ={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{bmatrix}}={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{pmatrix}}.}$$ $${\displaystyle \mathbf {A} =\left(a_{ij}\right),\quad \left[a_{ij}\right],\quad {\text{or}}\quad \left(a_{ij}\right)_{1\leq i\leq m,\;1\leq j\leq n}}$$ ${\displaystyle \mathbf {A} =(a_{i,j})_{1\leq i,j\leq n}}$ ${\displaystyle n=m}$

Las matrices se simbolizan generalmente con letras mayúsculas (como en los ejemplos anteriores), mientras que las letras minúsculas correspondientes , con dos índices subscritos (por ejemplo, o ), representan las entradas. Además de utilizar letras mayúsculas para simbolizar matrices, muchos autores utilizan un estilo tipográfico especial , comúnmente Roman en negrita (no cursiva), para distinguir aún más las matrices de otros objetos matemáticos. Una notación alternativa implica el uso de un doble subrayado con el nombre de la variable, con o sin estilo en negrita, como en . ${\displaystyle {\mathbf {A} }}$ ${\displaystyle {a_{11}}}$ ${\displaystyle {a_{1,1}}}$ ${\displaystyle {\underline {\underline {A}}}}$

La entrada en la fila i y la columna j de una matriz A se denomina a veces entrada o de la matriz y se denota comúnmente por o . Las notaciones alternativas para esa entrada son y . Por ejemplo, la entrada de la siguiente matriz es 5 (también denotada como , o ) : ${\displaystyle {i,j}}$ ${\displaystyle {(i,j)}}$ ${\displaystyle {a_{i,j}}}$ ${\displaystyle {a_{ij}}}$ ${\displaystyle {\mathbf {A} [i,j]}}$ ${\displaystyle {\mathbf {A} _{i,j}}}$ ${\displaystyle (1,3)}$ ${\displaystyle \mathbf {A} }$ ${\displaystyle {a_{13}}}$ ${\displaystyle {a_{1,3}}}$ ${\displaystyle \mathbf {A} [1,3]}$ ${\displaystyle {{\mathbf {A} }_{1,3}}}$

${\displaystyle \mathbf {A} ={\begin{bmatrix}4&-7&\color {red}{5}&0\\-2&0&11&8\\19&1&-3&12\end{bmatrix}}}$

A veces, las entradas de una matriz se pueden definir mediante una fórmula como . Por ejemplo, cada una de las entradas de la siguiente matriz está determinada por la fórmula . ${\displaystyle a_{i,j}=f(i,j)}$ ${\displaystyle \mathbf {A} }$ ${\displaystyle a_{ij}=i-j}$

${\displaystyle \mathbf {A} ={\begin{bmatrix}0&-1&-2&-3\\1&0&-1&-2\\2&1&0&-1\end{bmatrix}}}$

En este caso, la propia matriz a veces se define mediante esa fórmula, entre corchetes o paréntesis dobles. Por ejemplo, la matriz anterior se define como o . Si el tamaño de la matriz es , la fórmula mencionada anteriormente es válida para cualquier y cualquier . Esto se puede especificar por separado o indicar utilizando como subíndice. Por ejemplo, la matriz anterior es , y se puede definir como o . ${\displaystyle {\mathbf {A} }=[i-j]}$ ${\displaystyle {\mathbf {A} }=((i-j))}$ ${\displaystyle m\times n}$ ${\displaystyle f(i,j)}$ ${\displaystyle i=1,\dots ,m}$ ${\displaystyle j=1,\dots ,n}$ ${\displaystyle m\times n}$ ${\displaystyle \mathbf {A} }$ ${\displaystyle 3\times 4}$ ${\displaystyle {\mathbf {A} }=[i-j](i=1,2,3;j=1,\dots ,4)}$ ${\displaystyle {\mathbf {A} }=[i-j]_{3\times 4}}$

Algunos lenguajes de programación utilizan matrices con subíndice doble (o matrices de matrices) para representar una matriz de m por n . Algunos lenguajes de programación comienzan la numeración de los índices de las matrices en cero, en cuyo caso las entradas de una matriz de m por n se indexan mediante y . ^[6] Este artículo sigue la convención más común en la escritura matemática, donde la enumeración comienza desde 1 . ${\displaystyle 0\leq i\leq m-1}$ ${\displaystyle 0\leq j\leq n-1}$

El conjunto de todas las matrices reales m por n se denota a menudo como o El conjunto de todas las matrices m por n sobre otro cuerpo , o sobre un anillo R , se denota de manera similar como o Si m = n , como en el caso de matrices cuadradas , no se repite la dimensión: o ^[7] A menudo, , o , se utiliza en lugar de ${\displaystyle {\mathcal {M}}(m,n),}$ ${\displaystyle {\mathcal {M}}_{m\times n}(\mathbb {R} ).}$ ${\displaystyle {\mathcal {M}}(m,n,R),}$ ${\displaystyle {\mathcal {M}}_{m\times n}(R).}$   ${\displaystyle {\mathcal {M}}(n,R),}$ ${\displaystyle {\mathcal {M}}_{n}(R).}$ ${\displaystyle M}$ ${\displaystyle \operatorname {Mat} }$ ${\displaystyle {\mathcal {M}}.}$

Operaciones básicas

Se pueden aplicar varias operaciones básicas a las matrices. Algunas, como la transposición y la submatriz, no dependen de la naturaleza de las entradas. Otras, como la suma de matrices , la multiplicación escalar , la multiplicación de matrices y las operaciones de fila , implican operaciones sobre las entradas de la matriz y, por lo tanto, requieren que las entradas de la matriz sean números o pertenezcan a un cuerpo o un anillo . ^[8]

En esta sección, se supone que las entradas de la matriz pertenecen a un anillo fijo, que normalmente es un campo de números.

Suma, multiplicación escalar, resta y transposición

Suma

La suma A + B de dos matrices A y B de m por n se calcula entrada por entrada:

( A + B ) _{i , j} = A _{i , j} + B _{i , j} , donde 1 ≤ i ≤ m y 1 ≤ j ≤ n .

Por ejemplo,

${\displaystyle {\begin{bmatrix}1&3&1\\1&0&0\end{bmatrix}}+{\begin{bmatrix}0&0&5\\7&5&0\end{bmatrix}}={\begin{bmatrix}1+0&3+0&1+5\\1+7&0+5&0+0\end{bmatrix}}={\begin{bmatrix}1&3&6\\8&5&0\end{bmatrix}}}$

Multiplicación escalar

El producto c A de un número c (también llamado escalar en este contexto) y una matriz A se calcula multiplicando cada entrada de A por c :

( c A ) _{i , j} = c · A _{i , j} .

Esta operación se denomina multiplicación escalar , pero su resultado no se denomina "producto escalar" para evitar confusiones, ya que "producto escalar" se suele utilizar como sinónimo de " producto interno ". Por ejemplo:

${\displaystyle 2\cdot {\begin{bmatrix}1&8&-3\\4&-2&5\end{bmatrix}}={\begin{bmatrix}2\cdot 1&2\cdot 8&2\cdot -3\\2\cdot 4&2\cdot -2&2\cdot 5\end{bmatrix}}={\begin{bmatrix}2&16&-6\\8&-4&10\end{bmatrix}}}$

Sustracción

La resta de dos matrices m × n se define componiendo la suma de matrices con la multiplicación escalar por –1 :

${\displaystyle \mathbf {A} -\mathbf {B} =\mathbf {A} +(-1)\cdot \mathbf {B} }$

Transposición

La transpuesta de una matriz A de m por n es la matriz A de n por m (también denotada A ^tr o ^t A ) formada al convertir filas ^en columnas y viceversa:

( AT ) _{i , j} = A _{j , i} .^​

Por ejemplo:

${\displaystyle {\begin{bmatrix}1&2&3\\0&-6&7\end{bmatrix}}^{\mathrm {T} }={\begin{bmatrix}1&0\\2&-6\\3&7\end{bmatrix}}}$

Las propiedades familiares de los números se extienden a estas operaciones con matrices: por ejemplo, la adición es conmutativa , es decir, la suma de matrices no depende del orden de los sumandos: A  + B = B + A . ^[9] La transpuesta es compatible con la adición y la multiplicación escalar, como se expresa por ( c A ) ^T = c ( A ^T ) y ( A + B ) ^T = A ^T + B ^T . Finalmente, ( A ^T ) ^T = A .             

Multiplicación de matrices

Representación esquemática del producto matricial AB de dos matrices A y B

La multiplicación de dos matrices se define si y solo si el número de columnas de la matriz izquierda es igual al número de filas de la matriz derecha. Si A es una matriz de m por n y B es una matriz de n por p , entonces su producto matricial AB es la matriz de m por p cuyos valores están dados por el producto escalar de la fila correspondiente de A y la columna correspondiente de B : ^[10]

${\displaystyle [\mathbf {AB} ]_{i,j}=a_{i,1}b_{1,j}+a_{i,2}b_{2,j}+\cdots +a_{i,n}b_{n,j}=\sum _{r=1}^{n}a_{i,r}b_{r,j},}$

donde 1 ≤ i ≤ m y 1 ≤ j ≤ p . ^[11] Por ejemplo, la entrada subrayada 2340 en el producto se calcula como (2 × 1000) + (3 × 100) + (4 × 10) = 2340:

${\displaystyle {\begin{aligned}{\begin{bmatrix}{\underline {2}}&{\underline {3}}&{\underline {4}}\\1&0&0\\\end{bmatrix}}{\begin{bmatrix}0&{\underline {1000}}\\1&{\underline {100}}\\0&{\underline {10}}\\\end{bmatrix}}&={\begin{bmatrix}3&{\underline {2340}}\\0&1000\\\end{bmatrix}}.\end{aligned}}}$

La multiplicación de matrices satisface las reglas ( AB ) C = A ( BC ) ( asociatividad ), y ( A + B ) C = AC + BC así como C ( A + B ) = CA + CB ( distributividad izquierda y derecha ), siempre que el tamaño de las matrices sea tal que los diversos productos estén definidos. ^[12] El producto AB puede definirse sin que se defina BA , es decir, si A y B son matrices m por n y n por k , respectivamente, y m ≠ k . Incluso si ambos productos están definidos, generalmente no necesitan ser iguales, es decir:

AB ≠ BA ,

En otras palabras, la multiplicación de matrices no es conmutativa , en marcado contraste con los números (racionales, reales o complejos), cuyo producto es independiente del orden de los factores. ^[10] Un ejemplo de dos matrices que no conmutan entre sí es:

${\displaystyle {\begin{bmatrix}1&2\\3&4\\\end{bmatrix}}{\begin{bmatrix}0&1\\0&0\\\end{bmatrix}}={\begin{bmatrix}0&1\\0&3\\\end{bmatrix}},}$

mientras

${\displaystyle {\begin{bmatrix}0&1\\0&0\\\end{bmatrix}}{\begin{bmatrix}1&2\\3&4\\\end{bmatrix}}={\begin{bmatrix}3&4\\0&0\\\end{bmatrix}}.}$

Además de la multiplicación de matrices ordinaria que acabamos de describir, también existen otras operaciones con matrices menos utilizadas que pueden considerarse formas de multiplicación, como el producto de Hadamard y el producto de Kronecker . ^[13] Surgen al resolver ecuaciones matriciales como la ecuación de Sylvester .

Operaciones de fila

Hay tres tipos de operaciones de fila:

1. suma de filas, es decir agregar una fila a otra.
2. multiplicación de filas, es decir, multiplicar todas las entradas de una fila por una constante distinta de cero;
3. cambio de filas, es decir, intercambiar dos filas de una matriz;

Estas operaciones se utilizan de varias maneras, incluida la resolución de ecuaciones lineales y la búsqueda de inversas de matrices .

Submatriz

Una submatriz de una matriz es una matriz que se obtiene eliminando cualquier conjunto de filas y/o columnas. ^{[14] [15] [16]} Por ejemplo, a partir de la siguiente matriz de 3 por 4, podemos construir una submatriz de 2 por 3 eliminando la fila 3 y la columna 2:

${\displaystyle \mathbf {A} ={\begin{bmatrix}1&\color {red}{2}&3&4\\5&\color {red}{6}&7&8\\\color {red}{9}&\color {red}{10}&\color {red}{11}&\color {red}{12}\end{bmatrix}}\rightarrow {\begin{bmatrix}1&3&4\\5&7&8\end{bmatrix}}.}$

Los menores y cofactores de una matriz se encuentran calculando el determinante de ciertas submatrices. ^{[16] [17]}

Una submatriz principal es una submatriz cuadrada que se obtiene eliminando ciertas filas y columnas. La definición varía de un autor a otro. Según algunos autores, una submatriz principal es una submatriz en la que el conjunto de índices de fila que quedan es el mismo que el conjunto de índices de columna que quedan. ^{[18] [19]} Otros autores definen una submatriz principal como aquella en la que las primeras k filas y columnas, para algún número k , son las que quedan; ^[20] este tipo de submatriz también se ha denominado submatriz principal principal . ^[21]

Ecuaciones lineales

Las matrices se pueden utilizar para escribir y trabajar de forma compacta con múltiples ecuaciones lineales, es decir, sistemas de ecuaciones lineales. Por ejemplo, si A es una matriz de m por n , x designa un vector columna (es decir, una matriz de n × 1) de n variables x ₁ , x ₂ , ..., x _n , y b es un vector columna de m × 1, entonces la ecuación matricial

${\displaystyle \mathbf {Ax} =\mathbf {b} }$

es equivalente al sistema de ecuaciones lineales ^[22]

${\displaystyle {\begin{aligned}a_{1,1}x_{1}+a_{1,2}x_{2}+&\cdots +a_{1,n}x_{n}=b_{1}\\&\ \ \vdots \\a_{m,1}x_{1}+a_{m,2}x_{2}+&\cdots +a_{m,n}x_{n}=b_{m}\end{aligned}}}$

Usando matrices, esto se puede resolver de manera más compacta de lo que sería posible escribiendo todas las ecuaciones por separado. Si n = m y las ecuaciones son independientes , entonces esto se puede hacer escribiendo

${\displaystyle \mathbf {x} =\mathbf {A} ^{-1}\mathbf {b} }$

donde A ⁻¹ es la matriz inversa de A . Si A no tiene inversa, las soluciones (si las hay) se pueden encontrar utilizando su inversa generalizada .

Transformaciones lineales

Los vectores representados por una matriz de 2x2 corresponden a los lados de un cuadrado unitario transformado en paralelogramo.

Las matrices y la multiplicación de matrices revelan sus características esenciales cuando se relacionan con las transformaciones lineales , también conocidas como aplicaciones lineales . Una matriz real m por n A da lugar a una transformación lineal R ⁿ → R ^m que asigna cada vector x en R ⁿ al producto (matricial) Ax , que es un vector en R ^m . A la inversa, cada transformación lineal f : R ⁿ → R ^m surge de una matriz única m por n A : explícitamente, la entrada ( i , j ) de A es la i ^ésima coordenada de f ( e _j ), donde e _j = (0,...,0,1,0,...,0) es el vector unitario con 1 en la j ^ésima posición y 0 en el resto. Se dice que la matriz A representa la aplicación lineal f , y A se denomina matriz de transformación de f .

Por ejemplo, la matriz 2×2

${\displaystyle \mathbf {A} ={\begin{bmatrix}a&c\\b&d\end{bmatrix}}}$

puede verse como la transformación del cuadrado unitario en un paralelogramo con vértices en (0, 0) , ( a , b ) , ( a + c , b + d ) y ( c , d ) . El paralelogramo que se muestra a la derecha se obtiene multiplicando A por cada uno de los vectores columna , y , a su vez. Estos vectores definen los vértices del cuadrado unitario. ${\displaystyle {\begin{bmatrix}0\\0\end{bmatrix}},{\begin{bmatrix}1\\0\end{bmatrix}},{\begin{bmatrix}1\\1\end{bmatrix}}}$ ${\displaystyle {\begin{bmatrix}0\\1\end{bmatrix}}}$

La siguiente tabla muestra varias matrices reales de 2×2 con las funciones lineales asociadas de R ² . El original azul se asigna a la cuadrícula y las formas verdes . El origen (0,0) está marcado con un punto negro.

Bajo la correspondencia 1 a 1 entre matrices y aplicaciones lineales, la multiplicación de matrices corresponde a la composición de aplicaciones: ^[23] si una matriz B de k por m representa otra aplicación lineal g : R ^m → R ^k , entonces la composición g ∘ f está representada por BA ya que

( g ∘ f )( x ) = g ( f ( x )) = g ( Ax ) = B ( Ax ) = ( BA ) x .

La última igualdad se deriva de la asociatividad de la multiplicación de matrices antes mencionada.

El rango de una matriz A es el número máximo de vectores fila linealmente independientes de la matriz, que es el mismo que el número máximo de vectores columna linealmente independientes. ^[24] Equivalentemente, es la dimensión de la imagen del mapa lineal representado por A . ^[25] El teorema de rango-nulidad establece que la dimensión del núcleo de una matriz más el rango es igual al número de columnas de la matriz. ^[26]

Matriz cuadrada

Una matriz cuadrada es una matriz con el mismo número de filas y columnas. ^[5] Una matriz n por n se conoce como matriz cuadrada de orden n. Se pueden sumar y multiplicar dos matrices cuadradas cualesquiera del mismo orden. Las entradas a _ii forman la diagonal principal de una matriz cuadrada. Se encuentran en la línea imaginaria que va desde la esquina superior izquierda hasta la esquina inferior derecha de la matriz.

Tipos principales

Matriz diagonal y triangular

Si todas las entradas de A por debajo de la diagonal principal son cero, A se denomina matriz triangular superior . De manera similar, si todas las entradas de A por encima de la diagonal principal son cero, A se denomina matriz triangular inferior . Si todas las entradas fuera de la diagonal principal son cero, A se denomina matriz diagonal .

Matriz de identidad

La matriz identidad I _n de tamaño n es la matriz n por n en la que todos los elementos de la diagonal principal son iguales a 1 y todos los demás elementos son iguales a 0, por ejemplo,

${\displaystyle \mathbf {I} _{1}={\begin{bmatrix}1\end{bmatrix}},\ \mathbf {I} _{2}={\begin{bmatrix}1&0\\0&1\end{bmatrix}},\ \ldots ,\ \mathbf {I} _{n}={\begin{bmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{bmatrix}}}$

Es una matriz cuadrada de orden n y también un tipo especial de matriz diagonal . Se llama matriz identidad porque la multiplicación por ella deja la matriz inalterada:

AI _n = I _m A = A para cualquiermatriz m por n A .

Un múltiplo escalar distinto de cero de una matriz identidad se denomina matriz escalar . Si las entradas de la matriz provienen de un cuerpo, las matrices escalares forman un grupo, en virtud de la multiplicación de matrices, que es isomorfo al grupo multiplicativo de elementos distintos de cero del cuerpo.

Matriz simétrica o antisimétrica

Una matriz cuadrada A que es igual a su transpuesta, es decir, A = A ^T , es una matriz simétrica . Si, en cambio, A es igual al negativo de su transpuesta, es decir, A = − A ^T , entonces A es una matriz antisimétrica . En matrices complejas, la simetría se suele sustituir por el concepto de matrices hermíticas , que satisface A ^∗ = A , donde la estrella o asterisco denota la transpuesta conjugada de la matriz, es decir, la transpuesta del conjugado complejo de A .

Por el teorema espectral , las matrices simétricas reales y las matrices hermíticas complejas tienen una base propia ; es decir, cada vector es expresable como una combinación lineal de vectores propios. En ambos casos, todos los valores propios son reales. ^[27] Este teorema se puede generalizar a situaciones de dimensión infinita relacionadas con matrices con infinitas filas y columnas, véase más abajo.

Matriz invertible y su inversa

Una matriz cuadrada A se llama invertible o no singular si existe una matriz B tal que

AB = BA = In _, ^{[28] [29} ]

donde I _n es la matriz identidad n × n con 1 en la diagonal principal y 0 en el resto. Si B existe, es única y se denomina matriz inversa de A , denotada A ⁻¹ .

Matriz definida

Una matriz real simétrica A se llama definida positiva si la forma cuadrática asociada

f  ( x ) = x ^T A  x

tiene un valor positivo para cada vector distinto de cero x en R ⁿ . Si f  ( x ) solo produce valores negativos, entonces A es definida negativamente ; si f produce valores negativos y positivos, entonces A es indefinida . ^[30] Si la forma cuadrática f produce solo valores no negativos (positivos o cero), la matriz simétrica se llama semidefinida positiva (o si solo produce valores no positivos, entonces semidefinida negativa); por lo tanto, la matriz es indefinida precisamente cuando no es ni semidefinida positiva ni semidefinida negativa.

Una matriz simétrica es positiva-definida si y sólo si todos sus valores propios son positivos, es decir, la matriz es positiva-semidefinida y es invertible. ^[31] La tabla de la derecha muestra dos posibilidades para matrices de 2 por 2.

Al permitir como entrada dos vectores diferentes, se obtiene la forma bilineal asociada a A : ^[32]

B _A ( x , y ) = x ^T Ay .

En el caso de matrices complejas, se aplican la misma terminología y resultado, con matriz simétrica , forma cuadrática , forma bilineal y transpuesta x ^T reemplazadas respectivamente por matriz hermítica , forma hermítica , forma sesquilineal y transpuesta conjugada x ^H.

Matriz ortogonal

Una matriz ortogonal es una matriz cuadrada con elementos reales cuyas columnas y filas son vectores unitarios ortogonales (es decir, vectores ortonormales ). De manera equivalente, una matriz A es ortogonal si su transpuesta es igual a su inversa :

${\displaystyle \mathbf {A} ^{\mathrm {T} }=\mathbf {A} ^{-1},\,}$

Lo que implica

${\displaystyle \mathbf {A} ^{\mathrm {T} }\mathbf {A} =\mathbf {A} \mathbf {A} ^{\mathrm {T} }=\mathbf {I} _{n},}$

donde I _n es la matriz identidad de tamaño n .

Una matriz ortogonal A es necesariamente invertible (con inversa A ⁻¹ = A ^T ), unitaria ( A ⁻¹ = A * ), y normal ( A * A = AA * ). El determinante de cualquier matriz ortogonal es +1 o −1 . Una matriz ortogonal especial es una matriz ortogonal con determinante +1. Como transformación lineal , toda matriz ortogonal con determinante +1 es una rotación pura sin reflexión, es decir, la transformación conserva la orientación de la estructura transformada, mientras que toda matriz ortogonal con determinante -1 invierte la orientación, es decir, es una composición de una reflexión pura y una rotación (posiblemente nula). Las matrices identidad tienen determinante 1 y son rotaciones puras por un ángulo cero.

El análogo complejo de una matriz ortogonal es una matriz unitaria .

Operaciones principales

Rastro

La traza tr( A ) de una matriz cuadrada A es la suma de sus elementos diagonales. Si bien la multiplicación de matrices no es conmutativa como se mencionó anteriormente, la traza del producto de dos matrices es independiente del orden de los factores:

${\displaystyle \operatorname {tr} (\mathbf {AB} )=\operatorname {tr} (\mathbf {BA} )}$.

Esto se desprende inmediatamente de la definición de multiplicación de matrices:

${\displaystyle \operatorname {tr} (\mathbf {AB} )=\sum _{i=1}^{m}\sum _{j=1}^{n}a_{ij}b_{ji}=\operatorname {tr} (\mathbf {BA} ).}$

De ello se deduce que la traza del producto de más de dos matrices es independiente de las permutaciones cíclicas de las matrices, sin embargo, esto no se aplica en general a permutaciones arbitrarias (por ejemplo, tr( ABC ) ≠ tr( BAC ), en general). Además, la traza de una matriz es igual a la de su transpuesta, es decir,

^tr ( A ) = tr( AT ) .

Determinante

Una transformación lineal sobre R ² dada por la matriz indicada. El determinante de esta matriz es −1, ya que el área del paralelogramo verde de la derecha es 1, pero la función invierte la orientación , ya que cambia la orientación de los vectores en sentido antihorario por una en el sentido horario.

El determinante de una matriz cuadrada A (denotado det( A ) o | A |) es un número que codifica ciertas propiedades de la matriz. Una matriz es invertible si y solo si su determinante es distinto de cero. Su valor absoluto es igual al área (en R ² ) o al volumen (en R ³ ) de la imagen del cuadrado (o cubo) unitario, mientras que su signo corresponde a la orientación de la función lineal correspondiente: el determinante es positivo si y solo si se conserva la orientación.

El determinante de matrices de 2 por 2 viene dado por

${\displaystyle \det {\begin{bmatrix}a&b\\c&d\end{bmatrix}}=ad-bc.}$^[33]

El determinante de matrices de 3 x 3 implica 6 términos ( regla de Sarrus ). La fórmula de Leibniz, más extensa, generaliza estas dos fórmulas a todas las dimensiones. ^[34]

El determinante de un producto de matrices cuadradas es igual al producto de sus determinantes:

det( AB ) = det( A ) · det( B ), o usando notación alternativa:

| AB | = | A | · | B |. ^[35]

La suma de un múltiplo de cualquier fila a otra fila, o un múltiplo de cualquier columna a otra columna, no cambia el determinante. Intercambiar dos filas o dos columnas afecta al determinante multiplicándolo por −1. ^[36] Usando estas operaciones, cualquier matriz puede transformarse en una matriz triangular inferior (o superior), y para tales matrices, el determinante es igual al producto de las entradas en la diagonal principal; esto proporciona un método para calcular el determinante de cualquier matriz. Finalmente, la expansión de Laplace expresa el determinante en términos de menores , es decir, determinantes de matrices más pequeñas. ^[37] Esta expansión puede usarse para una definición recursiva de determinantes (tomando como caso inicial el determinante de una matriz 1 por 1, que es su única entrada, o incluso el determinante de una matriz 0 por 0, que es 1), que puede verse como equivalente a la fórmula de Leibniz. Los determinantes se pueden utilizar para resolver sistemas lineales utilizando la regla de Cramer , donde la división de los determinantes de dos matrices cuadradas relacionadas equivale al valor de cada una de las variables del sistema. ^[38]

Valores propios y vectores propios

Un número y un vector distinto de cero v que satisfacen ${\textstyle \lambda }$

${\displaystyle \mathbf {A} \mathbf {v} =\lambda \mathbf {v} }$

se denominan valor propio y vector propio de A , respectivamente. ^{[39] [40]} El número λ es un valor propio de una matriz n × n A si y solo si A −λ I _n no es invertible, lo que es equivalente a

${\displaystyle \det(\mathbf {A} -\lambda \mathbf {I} )=0.}$^[41]

El polinomio p _A en una indeterminada X dada por la evaluación del determinante det( X I _n − A ) se llama polinomio característico de A . Es un polinomio mónico de grado n . Por lo tanto, la ecuación polinómica p _A (λ)  =  0 tiene como máximo n soluciones diferentes, es decir, valores propios de la matriz. ^[42] Pueden ser complejos incluso si las entradas de A son reales. Según el teorema de Cayley-Hamilton , p _A ( A ) = 0 , es decir, el resultado de sustituir la propia matriz en su polinomio característico produce la matriz cero .

Aspectos computacionales

Los cálculos matriciales se pueden realizar a menudo con diferentes técnicas. Muchos problemas se pueden resolver tanto con algoritmos directos como con enfoques iterativos. Por ejemplo, los vectores propios de una matriz cuadrada se pueden obtener hallando una secuencia de vectores x _n que convergen a un vector propio cuando n tiende a infinito . ^[43]

Para elegir el algoritmo más adecuado para cada problema específico, es importante determinar tanto la efectividad como la precisión de todos los algoritmos disponibles. El dominio que estudia estas cuestiones se denomina álgebra lineal numérica . ^[44] Como ocurre con otras situaciones numéricas, dos aspectos principales son la complejidad de los algoritmos y su estabilidad numérica .

Determinar la complejidad de un algoritmo significa encontrar límites superiores o estimaciones de cuántas operaciones elementales, como sumas y multiplicaciones de escalares, son necesarias para realizar algún algoritmo, por ejemplo, la multiplicación de matrices . Calcular el producto matricial de dos matrices n por n utilizando la definición dada anteriormente necesita n ³ multiplicaciones, ya que para cualquiera de las n ² entradas del producto, son necesarias n multiplicaciones. El algoritmo de Strassen supera a este algoritmo "ingenuo"; necesita solo n ^2,807 multiplicaciones. ^[45] Un enfoque refinado también incorpora características específicas de los dispositivos informáticos.

En muchas situaciones prácticas, se conoce información adicional sobre las matrices involucradas. Un caso importante son las matrices dispersas , es decir, matrices cuya mayoría de entradas son cero. Existen algoritmos específicamente adaptados para, por ejemplo, resolver sistemas lineales Ax = b para matrices dispersas A , como el método del gradiente conjugado . ^[46]

Un algoritmo es, en términos generales, numéricamente estable si pequeñas desviaciones en los valores de entrada no conducen a grandes desviaciones en el resultado. Por ejemplo, calcular la inversa de una matriz mediante la expansión de Laplace (adj( A ) denota la matriz adjunta de A )

A ⁻¹ = adj( A ) / det( A )

Puede dar lugar a errores de redondeo significativos si el determinante de la matriz es muy pequeño. La norma de una matriz se puede utilizar para capturar el condicionamiento de problemas algebraicos lineales, como el cálculo de la inversa de una matriz. ^[47]

La mayoría de los lenguajes de programación informática admiten matrices, pero no están diseñados con comandos integrados para matrices. En cambio, las bibliotecas externas disponibles proporcionan operaciones matriciales en matrices, en casi todos los lenguajes de programación utilizados actualmente. La manipulación de matrices fue una de las primeras aplicaciones numéricas de las computadoras. ^[48] El BASIC Dartmouth original tenía comandos integrados para aritmética matricial en matrices desde su implementación de la segunda edición en 1964. Ya en la década de 1970, algunas computadoras de escritorio de ingeniería como la HP 9830 tenían cartuchos ROM para agregar comandos BASIC para matrices . Algunos lenguajes informáticos como APL fueron diseñados para manipular matrices, y se pueden usar varios programas matemáticos para ayudar a la computación con matrices. ^[49] A partir de 2023, la mayoría de las computadoras tienen algún tipo de operaciones matriciales integradas a un nivel bajo que implementan la especificación BLAS estándar , en la que se basan la mayoría de las bibliotecas de álgebra lineal y de matriz de nivel superior (por ejemplo, EISPACK , LINPACK , LAPACK ). Si bien la mayoría de estas bibliotecas requieren un nivel profesional de codificación, se puede acceder a LAPACK mediante enlaces de nivel superior (y fáciles de usar) como NumPy / SciPy , R , GNU Octave , MATLAB .

Descomposición

Existen varios métodos para convertir las matrices en una forma más accesible. Generalmente se las conoce como técnicas de descomposición matricial o factorización matricial . El interés de todas estas técnicas es que preservan ciertas propiedades de las matrices en cuestión, como el determinante, el rango o la inversa, de modo que estas cantidades se puedan calcular después de aplicar la transformación, o que ciertas operaciones matriciales sean algorítmicamente más fáciles de llevar a cabo para algunos tipos de matrices.

La descomposición LU factoriza matrices como un producto de matrices triangulares inferior ( L ) y superior ( U ). ^[50] Una vez calculada esta descomposición, los sistemas lineales se pueden resolver de manera más eficiente, mediante una técnica simple llamada sustitución hacia adelante y hacia atrás . Asimismo, las inversas de matrices triangulares son algorítmicamente más fáciles de calcular. La eliminación gaussiana es un algoritmo similar; transforma cualquier matriz a forma escalonada por filas . ^[51] Ambos métodos proceden multiplicando la matriz por matrices elementales adecuadas , que corresponden a permutar filas o columnas y agregar múltiplos de una fila a otra fila. La descomposición en valores singulares expresa cualquier matriz A como un producto UDV ^∗ , donde U y V son matrices unitarias y D es una matriz diagonal.

Ejemplo de matriz en forma normal de Jordan. Los bloques grises se denominan bloques de Jordan.

La descomposición propia o diagonalización expresa A como un producto VDV ⁻¹ , donde D es una matriz diagonal y V es una matriz invertible adecuada. ^[52] Si A se puede escribir en esta forma, se llama diagonalizable . De manera más general, y aplicable a todas las matrices, la descomposición de Jordan transforma una matriz en forma normal de Jordan , es decir, matrices cuyas únicas entradas distintas de cero son los valores propios λ ₁ a λ _n de A , colocados en la diagonal principal y posiblemente entradas iguales a una directamente sobre la diagonal principal, como se muestra a la derecha. ^[53] Dada la descomposición propia, la n ^ésima potencia de A (es decir, la multiplicación de matrices iterada n veces) se puede calcular mediante

Un ^norte = ( VDV ⁻¹ ) ⁿ = VDV ⁻¹ VDV ⁻¹ ... VDV ⁻¹ = VD ⁿ V ⁻¹

y la potencia de una matriz diagonal se puede calcular tomando las potencias correspondientes de las entradas diagonales, lo que es mucho más fácil que hacer la exponenciación para A en su lugar. Esto se puede utilizar para calcular la exponencial matricial e ^A , una necesidad que surge con frecuencia al resolver ecuaciones diferenciales lineales , logaritmos matriciales y raíces cuadradas de matrices . ^[54] Para evitar situaciones numéricamente mal condicionadas , se pueden emplear otros algoritmos como la descomposición de Schur . ^[55]

Aspectos algebraicos abstractos y generalizaciones

Las matrices se pueden generalizar de diferentes maneras. El álgebra abstracta utiliza matrices con entradas en campos más generales o incluso anillos , mientras que el álgebra lineal codifica las propiedades de las matrices en la noción de mapas lineales. Es posible considerar matrices con infinitas columnas y filas. Otra extensión son los tensores , que pueden verse como matrices de números de dimensiones superiores, a diferencia de los vectores, que a menudo pueden realizarse como secuencias de números, mientras que las matrices son matrices rectangulares o bidimensionales de números. ^[56] Las matrices, sujetas a ciertos requisitos, tienden a formar grupos conocidos como grupos de matrices. De manera similar, bajo ciertas condiciones, las matrices forman anillos conocidos como anillos de matrices . Aunque el producto de matrices no es en general conmutativo, ciertas matrices forman campos conocidos como campos de matrices . En general, las matrices y su multiplicación también forman una categoría , la categoría de matrices .

Matrices con entradas más generales

Este artículo se centra en matrices cuyas entradas son números reales o complejos. Sin embargo, las matrices pueden considerarse con tipos de entradas mucho más generales que los números reales o complejos. Como primer paso de generalización, cualquier cuerpo , es decir, un conjunto donde las operaciones de suma , resta , multiplicación y división están definidas y se comportan bien, puede usarse en lugar de R o C , por ejemplo, números racionales o cuerpos finitos . Por ejemplo, la teoría de codificación hace uso de matrices sobre cuerpos finitos. Siempre que se consideren valores propios , como estos son raíces de un polinomio, pueden existir solo en un cuerpo más grande que el de las entradas de la matriz; por ejemplo, pueden ser complejos en el caso de una matriz con entradas reales. La posibilidad de reinterpretar las entradas de una matriz como elementos de un cuerpo más grande (por ejemplo, ver una matriz real como una matriz compleja cuyas entradas son todas reales) permite entonces considerar que cada matriz cuadrada posee un conjunto completo de valores propios. Alternativamente, se pueden considerar sólo matrices con entradas en un campo algebraicamente cerrado , como C , desde el principio.

De manera más general, las matrices con entradas en un anillo R se usan ampliamente en matemáticas. ^[57] Los anillos son una noción más general que los campos en el sentido de que no necesita existir una operación de división. Las mismas operaciones de adición y multiplicación de matrices se extienden también a este contexto. El conjunto M( n , R ) (también denotado M _n (R) ^[7] ) de todas las matrices cuadradas n -por- n sobre R es un anillo llamado anillo de matrices , isomorfo al anillo de endomorfismo del módulo R izquierdo R n . ^[ 58 ^] Si el anillo R es conmutativo , es decir, su multiplicación es conmutativa, entonces el anillo M( n , R ) es también un álgebra asociativa sobre R . El determinante de matrices cuadradas sobre un anillo conmutativo R todavía se puede definir utilizando la fórmula de Leibniz ; Una matriz de este tipo es invertible si y sólo si su determinante es invertible en R , generalizando la situación sobre un cuerpo F , donde cada elemento distinto de cero es invertible. ^[59] Las matrices sobre superanillos se denominan supermatrices . ^[60]

Las matrices no siempre tienen todas sus entradas en el mismo anillo  , o incluso en ningún anillo. Un caso especial pero común son las matrices de bloques , que pueden considerarse como matrices cuyas entradas son matrices. Las entradas no necesitan ser matrices cuadradas y, por lo tanto, no necesitan ser miembros de ningún anillo ; pero sus tamaños deben cumplir ciertas condiciones de compatibilidad.

Relación con los mapas lineales

Las aplicaciones lineales R ⁿ → R ^m son equivalentes a matrices de m por n , como se describió anteriormente. De manera más general, cualquier aplicación lineal f : V → W entre espacios vectoriales de dimensión finita se puede describir mediante una matriz A = ( a _ij ), después de elegir bases v ₁ , ..., v _n de V , y w ₁ , ..., w _m de W (por lo que n es la dimensión de V y m es la dimensión de W ), que es tal que

${\displaystyle f(\mathbf {v} _{j})=\sum _{i=1}^{m}a_{i,j}\mathbf {w} _{i}\qquad {\mbox{for}}\ j=1,\ldots ,n.}$

En otras palabras, la columna j de A expresa la imagen de v _j en términos de los vectores base w _I de W ; por lo tanto, esta relación determina de manera única las entradas de la matriz A . La matriz depende de la elección de las bases: diferentes elecciones de bases dan lugar a matrices diferentes, pero equivalentes . ^[61] Muchas de las nociones concretas anteriores pueden reinterpretarse a la luz de esto, por ejemplo, la matriz transpuesta A ^T describe la transpuesta de la función lineal dada por A , en relación con las bases duales . ^[62]

Estas propiedades se pueden replantear de forma más natural: la categoría de matrices con entradas en un campo con multiplicación como composición es equivalente a la categoría de espacios vectoriales de dimensión finita y mapas lineales sobre este campo. ^[63] ${\displaystyle k}$

De manera más general, el conjunto de matrices m × n se puede utilizar para representar las funciones R -lineales entre los módulos libres R ^m y R ⁿ para un anillo arbitrario R con unidad. Cuando n  = m es posible la composición de estas funciones, y esto da lugar al anillo matricial de matrices n × n que representa el anillo de endomorfismo de R ⁿ . 

Grupos matriciales

Un grupo es una estructura matemática que consiste en un conjunto de objetos junto con una operación binaria , es decir, una operación que combina dos objetos cualesquiera en un tercero, sujeto a ciertos requisitos. ^[64] Un grupo en el que los objetos son matrices y la operación del grupo es la multiplicación de matrices se llama grupo matricial . ^{[65] [66]} Dado que un grupo de cada elemento debe ser invertible, los grupos matriciales más generales son los grupos de todas las matrices invertibles de un tamaño dado, llamados grupos lineales generales .

Cualquier propiedad de matrices que se conserva bajo productos de matrices e inversas se puede utilizar para definir grupos de matrices adicionales. Por ejemplo, las matrices con un tamaño dado y con un determinante de 1 forman un subgrupo de (es decir, un grupo más pequeño contenido en) su grupo lineal general, llamado grupo lineal especial . ^[67] Matrices ortogonales , determinadas por la condición

MTM = yo ,^​​

forman el grupo ortogonal . ^[68] Toda matriz ortogonal tiene determinante 1 o −1. Las matrices ortogonales con determinante 1 forman un subgrupo llamado grupo ortogonal especial .

Todo grupo finito es isomorfo a un grupo matricial, como se puede ver al considerar la representación regular del grupo simétrico . ^[69] Los grupos generales se pueden estudiar utilizando grupos matriciales, que se entienden relativamente bien, utilizando la teoría de la representación . ^[70]

Matrices infinitas

También es posible considerar matrices con un número infinito de filas y/o columnas ^[71], aunque, al ser objetos infinitos, no se pueden escribir explícitamente. Lo único que importa es que para cada elemento del conjunto que indexa las filas y cada elemento del conjunto que indexa las columnas, existe una entrada bien definida (estos conjuntos de índices ni siquiera necesitan ser subconjuntos de los números naturales). Las operaciones básicas de suma, resta, multiplicación escalar y transposición aún se pueden definir sin problemas; sin embargo, la multiplicación de matrices puede implicar sumas infinitas para definir las entradas resultantes, y estas no están definidas en general.

Si R es un anillo cualquiera con unidad, entonces el anillo de endomorfismos de como módulo R derecho es isomorfo al anillo de matrices finitas de columna cuyas entradas están indexadas por , y cuyas columnas contienen cada una sólo un número finito de entradas distintas de cero. Los endomorfismos de M considerados como módulo R izquierdo dan como resultado un objeto análogo, las matrices finitas de fila cuyas filas tienen cada una sólo un número finito de entradas distintas de cero. ${\displaystyle M=\bigoplus _{i\in I}R}$ ${\displaystyle \mathrm {CFM} _{I}(R)}$ ${\displaystyle I\times I}$ ${\displaystyle \mathrm {RFM} _{I}(R)}$

Si se utilizan matrices infinitas para describir aplicaciones lineales, entonces sólo se pueden utilizar aquellas matrices cuyas columnas tengan sólo un número finito de entradas distintas de cero, por la siguiente razón. Para que una matriz A describa una aplicación lineal f : V → W , se deben haber elegido bases para ambos espacios; recuerde que por definición esto significa que cada vector en el espacio se puede escribir únicamente como una combinación lineal (finita) de vectores base, de modo que escrito como un vector (columna) ve de coeficientes , sólo un número finito de entradas v _I son distintas de cero. Ahora bien, las columnas de A describen las imágenes por f de vectores base individuales de V en la base de W , lo que sólo tiene sentido si estas columnas tienen sólo un número finito de entradas distintas de cero. Sin embargo, no hay ninguna restricción en las filas de A : en el producto A · v sólo hay un número finito de coeficientes distintos de cero de v involucrados, por lo que cada una de sus entradas, incluso si se da como una suma infinita de productos, implica sólo un número finito de términos distintos de cero y, por tanto, está bien definida. Además, esto equivale a formar una combinación lineal de las columnas de A que efectivamente involucra solo un número finito de ellas, por lo que el resultado solo tiene un número finito de entradas distintas de cero porque cada una de esas columnas lo hace. Los productos de dos matrices del tipo dado están bien definidos (siempre que los conjuntos de índice de columna y de índice de fila coincidan), son del mismo tipo y corresponden a la composición de aplicaciones lineales. 

Si R es un anillo normado , entonces la condición de finitud de filas o columnas puede ser relajada. Con la norma establecida, se pueden utilizar series absolutamente convergentes en lugar de sumas finitas. Por ejemplo, las matrices cuyas sumas de columnas son secuencias convergentes forman un anillo. Análogamente, las matrices cuyas sumas de filas son series convergentes también forman un anillo.

Las matrices infinitas también se pueden utilizar para describir operadores en espacios de Hilbert , donde surgen cuestiones de convergencia y continuidad , lo que a su vez da lugar a ciertas restricciones que deben imponerse. Sin embargo, el punto de vista explícito de las matrices tiende a ofuscar el asunto, ^[72] y se pueden utilizar en su lugar las herramientas abstractas y más poderosas del análisis funcional .

Matriz vacía

Una matriz vacía es una matriz en la que el número de filas o columnas (o ambas) es cero. ^{[73] [74]} Las matrices vacías ayudan a tratar con mapas que involucran el espacio vectorial cero . Por ejemplo, si A es una matriz de 3 por 0 y B es una matriz de 0 por 3, entonces AB es la matriz cero de 3 por 3 correspondiente al mapa nulo de un espacio tridimensional V a sí mismo, mientras que BA es una matriz de 0 por 0. No existe una notación común para las matrices vacías, pero la mayoría de los sistemas de álgebra computacional permiten crearlas y calcular con ellas. El determinante de la matriz de 0 por 0 es 1 de la siguiente manera con respecto al producto vacío que ocurre en la fórmula de Leibniz para el determinante como 1. Este valor también es consistente con el hecho de que el mapa identidad de cualquier espacio de dimensión finita a sí mismo tiene determinante  1, un hecho que a menudo se usa como parte de la caracterización de determinantes.

Aplicaciones

Existen numerosas aplicaciones de matrices, tanto en matemáticas como en otras ciencias. Algunas de ellas simplemente aprovechan la representación compacta de un conjunto de números en una matriz. Por ejemplo, en la teoría de juegos y la economía , la matriz de pagos codifica el pago para dos jugadores, dependiendo de cuál de un conjunto dado (finito) de estrategias elijan los jugadores. ^[75] La minería de texto y la compilación automatizada de tesauros utilizan matrices de términos de documento como tf-idf para rastrear frecuencias de ciertas palabras en varios documentos. ^[76]

Los números complejos se pueden representar mediante matrices reales particulares de 2 por 2 mediante

${\displaystyle a+ib\leftrightarrow {\begin{bmatrix}a&-b\\b&a\end{bmatrix}},}$

en las que la adición y la multiplicación de números complejos y matrices se corresponden entre sí. Por ejemplo, las matrices de rotación 2 por 2 representan la multiplicación por algún número complejo de valor absoluto 1, como se indicó anteriormente. Una interpretación similar es posible para los cuaterniones ^[77] y las álgebras de Clifford en general.

Las primeras técnicas de cifrado, como el cifrado Hill, también utilizaban matrices. Sin embargo, debido a la naturaleza lineal de las matrices, estos códigos son comparativamente fáciles de descifrar. ^[78] Los gráficos por computadora utilizan matrices para representar objetos; para calcular transformaciones de objetos utilizando matrices de rotación afín para realizar tareas como proyectar un objeto tridimensional en una pantalla bidimensional, correspondiente a una observación teórica de la cámara; y para aplicar convoluciones de imagen como nitidez, desenfoque, detección de bordes y más. ^[79] Las matrices sobre un anillo polinomial son importantes en el estudio de la teoría del control .

La química utiliza matrices de diversas maneras, en particular desde el uso de la teoría cuántica para analizar el enlace molecular y la espectroscopia . Algunos ejemplos son la matriz de superposición y la matriz de Fock, que se utilizan para resolver las ecuaciones de Roothaan y obtener los orbitales moleculares del método de Hartree-Fock .

Teoría de grafos

Un gráfico no dirigido con matriz de adyacencia: $${\displaystyle {\begin{bmatrix}1&1&0\\1&0&1\\0&1&0\end{bmatrix}}.}$$

La matriz de adyacencia de un grafo finito es una noción básica de la teoría de grafos . ^[80] Registra qué vértices del grafo están conectados por una arista. Las matrices que contienen solo dos valores diferentes (1 y 0 significan, por ejemplo, "sí" y "no", respectivamente) se denominan matrices lógicas . La matriz de distancia (o costo) contiene información sobre las distancias de las aristas. ^[81] Estos conceptos se pueden aplicar a sitios web conectados por hipervínculos o ciudades conectadas por carreteras, etc., en cuyo caso (a menos que la red de conexión sea extremadamente densa) las matrices tienden a ser dispersas , es decir, contienen pocas entradas distintas de cero. Por lo tanto, se pueden utilizar algoritmos matriciales específicamente diseñados en la teoría de redes .

Análisis y geometría

La matriz hessiana de una función diferenciable ƒ : R ⁿ → R consiste en las segundas derivadas de ƒ con respecto a las distintas direcciones de coordenadas, es decir, ^[82]

${\displaystyle H(f)=\left[{\frac {\partial ^{2}f}{\partial x_{i}\,\partial x_{j}}}\right].}$

En el punto de silla ( x  =  0, y  =  0) (rojo) de la función f ( x ,− y ) = x ² − y ² , la matriz hessiana es indefinida .    ${\displaystyle {\begin{bmatrix}2&0\\0&-2\end{bmatrix}}}$

Codifica información sobre el comportamiento de crecimiento local de la función: dado un punto crítico x  =  ( x ₁ ,  ..., x _n ), es decir, un punto donde las primeras derivadas parciales de ƒ se desvanecen, la función tiene un mínimo local si la matriz hessiana es definida positiva . La programación cuadrática se puede utilizar para encontrar mínimos o máximos globales de funciones cuadráticas estrechamente relacionadas con las asociadas a matrices (ver arriba). ^[83]  ${\displaystyle \partial f/\partial x_{i}}$

Otra matriz que se utiliza con frecuencia en situaciones geométricas es la matriz de Jacobi de una función diferenciable f : R ⁿ → R ^m . Si f ₁ , ..., f _m denotan los componentes de f , entonces la matriz de Jacobi se define como ^[84]

${\displaystyle J(f)=\left[{\frac {\partial f_{i}}{\partial x_{j}}}\right]_{1\leq i\leq m,1\leq j\leq n}.}$

Si n > m , y si el rango de la matriz de Jacobi alcanza su valor máximo m , f es localmente invertible en ese punto, por el teorema de la función implícita . ^[85]

Las ecuaciones diferenciales parciales se pueden clasificar considerando la matriz de coeficientes de los operadores diferenciales de orden superior de la ecuación. Para las ecuaciones diferenciales parciales elípticas esta matriz es definida positiva, lo que tiene una influencia decisiva en el conjunto de posibles soluciones de la ecuación en cuestión. ^[86]

El método de elementos finitos es un método numérico importante para resolver ecuaciones diferenciales parciales, ampliamente aplicado en la simulación de sistemas físicos complejos. Intenta aproximar la solución de alguna ecuación mediante funciones lineales por partes, donde las partes se eligen en relación con una cuadrícula suficientemente fina, que a su vez puede reformularse como una ecuación matricial. ^[87]

Teoría de la probabilidad y estadística

Dos cadenas de Markov diferentes. El gráfico muestra el número de partículas (de un total de 1000) en el estado "2". Ambos valores límite se pueden determinar a partir de las matrices de transición, que se indican en (rojo) y (negro). ${\displaystyle {\begin{bmatrix}0.7&0\\0.3&1\end{bmatrix}}}$ ${\displaystyle {\begin{bmatrix}0.7&0.2\\0.3&0.8\end{bmatrix}}}$

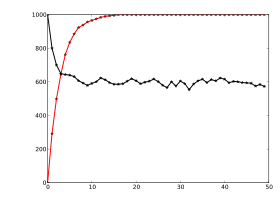
Las matrices estocásticas son matrices cuadradas cuyas filas son vectores de probabilidad , es decir, cuyas entradas no son negativas y suman uno. Las matrices estocásticas se utilizan para definir cadenas de Markov con un número finito de estados. ^{[88] Una fila de la matriz estocástica proporciona la distribución de probabilidad para la siguiente posición de alguna partícula que se encuentra actualmente en el estado que corresponde a la fila. Las propiedades de los} estados absorbentes similares a cadenas de Markov , es decir, estados que cualquier partícula alcanza eventualmente, se pueden leer a partir de los vectores propios de las matrices de transición. ^[89]

La estadística también utiliza matrices en muchas formas diferentes. ^[90] La estadística descriptiva se ocupa de describir conjuntos de datos, que a menudo se pueden representar como matrices de datos , que luego pueden someterse a técnicas de reducción de dimensionalidad . La matriz de covarianza codifica la varianza mutua de varias variables aleatorias . ^[91] Otra técnica que utiliza matrices son los mínimos cuadrados lineales , un método que aproxima un conjunto finito de pares ( x ₁ , y ₁ ), ( x ₂ , y ₂ ), ..., ( x _N , y _N ), mediante una función lineal

y _i ≈ ax _i + b , i = 1, ..., N

que puede formularse en términos de matrices, relacionadas con la descomposición en valores singulares de matrices. ^[92]

Las matrices aleatorias son matrices cuyas entradas son números aleatorios, sujetos a distribuciones de probabilidad adecuadas , como la distribución normal de matrices . Más allá de la teoría de la probabilidad, se aplican en dominios que van desde la teoría de números hasta la física . ^{[93] [94]}

Simetrías y transformaciones en física

Las transformaciones lineales y las simetrías asociadas desempeñan un papel clave en la física moderna. Por ejemplo, las partículas elementales en la teoría cuántica de campos se clasifican como representaciones del grupo de Lorentz de la relatividad especial y, más específicamente, por su comportamiento bajo el grupo de espín . Las representaciones concretas que involucran las matrices de Pauli y las matrices gamma más generales son una parte integral de la descripción física de los fermiones , que se comportan como espinores . ^[95] Para los tres quarks más ligeros , existe una representación teórica de grupos que involucra al grupo unitario especial SU(3); para sus cálculos, los físicos utilizan una representación matricial conveniente conocida como las matrices de Gell-Mann , que también se utilizan para el grupo de calibración SU(3) que forma la base de la descripción moderna de las interacciones nucleares fuertes, la cromodinámica cuántica . La matriz Cabibbo–Kobayashi–Maskawa , a su vez, expresa el hecho de que los estados básicos de los quarks que son importantes para las interacciones débiles no son los mismos que, sino que están relacionados linealmente con los estados básicos de los quarks que definen partículas con masas específicas y distintas . ^[96]

Combinaciones lineales de estados cuánticos

El primer modelo de mecánica cuántica ( Heisenberg , 1925) representó los operadores de la teoría mediante matrices de dimensión infinita que actúan sobre estados cuánticos. ^[97] Esto también se conoce como mecánica matricial . Un ejemplo particular es la matriz de densidad que caracteriza el estado "mixto" de un sistema cuántico como una combinación lineal de estados propios elementales, "puros" . ^[98]

Otra matriz sirve como herramienta clave para describir los experimentos de dispersión que forman la piedra angular de la física de partículas experimental: las reacciones de colisión como las que ocurren en los aceleradores de partículas , donde las partículas que no interactúan se dirigen unas hacia otras y chocan en una pequeña zona de interacción, con un nuevo conjunto de partículas que no interactúan como resultado, se pueden describir como el producto escalar de los estados de partículas salientes y una combinación lineal de los estados de partículas entrantes. La combinación lineal está dada por una matriz conocida como la matriz S , que codifica toda la información sobre las posibles interacciones entre partículas. ^[99]

Modos normales

Una aplicación general de las matrices en física es la descripción de sistemas armónicos acoplados linealmente. Las ecuaciones de movimiento de tales sistemas se pueden describir en forma matricial, con una matriz de masa que multiplica una velocidad generalizada para dar el término cinético, y una matriz de fuerza que multiplica un vector de desplazamiento para caracterizar las interacciones. La mejor manera de obtener soluciones es determinar los vectores propios del sistema , sus modos normales , diagonalizando la ecuación matricial. Técnicas como esta son cruciales cuando se trata de la dinámica interna de las moléculas : las vibraciones internas de sistemas que consisten en átomos componentes unidos mutuamente. ^[100] También son necesarias para describir vibraciones mecánicas y oscilaciones en circuitos eléctricos. ^[101]

Óptica geométrica

La óptica geométrica ofrece otras aplicaciones matriciales. En esta teoría aproximada, se descuida la naturaleza ondulatoria de la luz. El resultado es un modelo en el que los rayos de luz son, de hecho, rayos geométricos . Si la desviación de los rayos de luz por los elementos ópticos es pequeña, la acción de una lente o un elemento reflectante sobre un rayo de luz dado se puede expresar como la multiplicación de un vector de dos componentes por una matriz de dos por dos denominada análisis matricial de transferencia de rayos : los componentes del vector son la pendiente del rayo de luz y su distancia desde el eje óptico, mientras que la matriz codifica las propiedades del elemento óptico. Hay dos tipos de matrices, a saber, una matriz de refracción que describe la refracción en la superficie de una lente, y una matriz de traslación , que describe la traslación del plano de referencia a la siguiente superficie refractante, donde se aplica otra matriz de refracción. El sistema óptico, que consiste en una combinación de lentes y/o elementos reflectantes, se describe simplemente mediante la matriz resultante del producto de las matrices de los componentes. ^[102]

Electrónica

El análisis de malla tradicional y el análisis nodal en electrónica conducen a un sistema de ecuaciones lineales que pueden describirse con una matriz.

The behavior of many electronic components can be described using matrices. Let A be a 2-dimensional vector with the component's input voltage v₁ and input current I₁ as its elements, and let B be a 2-dimensional vector with the component's output voltage v₂ and output current I₂ as its elements. Then the behavior of the electronic component can be described by B = H · A, where H is a 2 x 2 matrix containing one impedance element (h₁₂), one admittance element (h₂₁), and two dimensionless elements (h₁₁ and h₂₂). Calculating a circuit now reduces to multiplying matrices.

History

Matrices have a long history of application in solving linear equations but they were known as arrays until the 1800s. The Chinese text The Nine Chapters on the Mathematical Art written in the 10th–2nd century BCE is the first example of the use of array methods to solve simultaneous equations,^[103] including the concept of determinants. In 1545 Italian mathematician Gerolamo Cardano introduced the method to Europe when he published Ars Magna.^[104] The Japanese mathematician Seki used the same array methods to solve simultaneous equations in 1683.^[105] The Dutch mathematician Jan de Witt represented transformations using arrays in his 1659 book Elements of Curves (1659).^[106] Between 1700 and 1710 Gottfried Wilhelm Leibniz publicized the use of arrays for recording information or solutions and experimented with over 50 different systems of arrays.^[104] Cramer presented his rule in 1750.

The term "matrix" (Latin for "womb", "dam" (non-human female animal kept for breeding), "source", "origin", "list", and "register", are derived from mater—mother^[107]) was coined by James Joseph Sylvester in 1850,^[108] who understood a matrix as an object giving rise to several determinants today called minors, that is to say, determinants of smaller matrices that derive from the original one by removing columns and rows. In an 1851 paper, Sylvester explains:^[109]

I have in previous papers defined a "Matrix" as a rectangular array of terms, out of which different systems of determinants may be engendered from the womb of a common parent.

Arthur Cayley published a treatise on geometric transformations using matrices that were not rotated versions of the coefficients being investigated as had previously been done. Instead, he defined operations such as addition, subtraction, multiplication, and division as transformations of those matrices and showed the associative and distributive properties held. Cayley investigated and demonstrated the non-commutative property of matrix multiplication as well as the commutative property of matrix addition.^[104] Early matrix theory had limited the use of arrays almost exclusively to determinants and Arthur Cayley's abstract matrix operations were revolutionary. He was instrumental in proposing a matrix concept independent of equation systems. In 1858 Cayley published his A memoir on the theory of matrices^[110][111] in which he proposed and demonstrated the Cayley–Hamilton theorem.^[104]

The English mathematician Cuthbert Edmund Cullis was the first to use modern bracket notation for matrices in 1913 and he simultaneously demonstrated the first significant use of the notation A = [a _I,j] to represent a matrix where a _I,j refers to the ith row and the jth column.^[104]

The modern study of determinants sprang from several sources.^[112] Number-theoretical problems led Gauss to relate coefficients of quadratic forms, that is, expressions such as x² + xy − 2y², and linear maps in three dimensions to matrices. Eisenstein further developed these notions, including the remark that, in modern parlance, matrix products are non-commutative. Cauchy was the first to prove general statements about determinants, using as the definition of the determinant of a matrix A = [a _i,j] the following: replace the powers a_j^k by a _jk in the polynomial

${\displaystyle a_{1}a_{2}\cdots a_{n}\prod _{i<j}(a_{j}-a_{i})\;}$,

where ${\displaystyle \textstyle \prod }$ denotes the product of the indicated terms. He also showed, in 1829, that the eigenvalues of symmetric matrices are real.^[113] Jacobi studied "functional determinants"—later called Jacobi determinants by Sylvester—which can be used to describe geometric transformations at a local (or infinitesimal) level, see above. Kronecker's Vorlesungen über die Theorie der Determinanten^[114] and Weierstrass' Zur Determinantentheorie,^[115] both published in 1903, first treated determinants axiomatically, as opposed to previous more concrete approaches such as the mentioned formula of Cauchy. At that point, determinants were firmly established.

Many theorems were first established for small matrices only, for example, the Cayley–Hamilton theorem was proved for 2×2 matrices by Cayley in the aforementioned memoir, and by Hamilton for 4×4 matrices. Frobenius, working on bilinear forms, generalized the theorem to all dimensions (1898). Also at the end of the 19th century, the Gauss–Jordan elimination (generalizing a special case now known as Gauss elimination) was established by Wilhelm Jordan. In the early 20th century, matrices attained a central role in linear algebra,^[116] partially due to their use in the classification of the hypercomplex number systems of the previous century.

The inception of matrix mechanics by Heisenberg, Born and Jordan led to studying matrices with infinitely many rows and columns.^[117] Later, von Neumann carried out the mathematical formulation of quantum mechanics, by further developing functional analytic notions such as linear operators on Hilbert spaces, which, very roughly speaking, correspond to Euclidean space, but with an infinity of independent directions.

Other historical usages of the word "matrix" in mathematics

The word has been used in unusual ways by at least two authors of historical importance.

Bertrand Russell and Alfred North Whitehead in their Principia Mathematica (1910–1913) use the word "matrix" in the context of their axiom of reducibility. They proposed this axiom as a means to reduce any function to one of lower type, successively, so that at the "bottom" (0 order) the function is identical to its extension:^[118]

Let us give the name of matrix to any function, of however many variables, that does not involve any apparent variables. Then, any possible function other than a matrix derives from a matrix using generalization, that is, by considering the proposition that the function in question is true with all possible values or with some value of one of the arguments, the other argument or arguments remaining undetermined.

For example, a function Φ(x, y) of two variables x and y can be reduced to a collection of functions of a single variable, for example, y, by "considering" the function for all possible values of "individuals" a_i substituted in place of a variable x. And then the resulting collection of functions of the single variable y, that is, ∀a_i: Φ(a_i, y), can be reduced to a "matrix" of values by "considering" the function for all possible values of "individuals" b_i substituted in place of variable y:

∀b_j∀a_i: Φ(a_i, b_j).

Alfred Tarski in his 1946 Introduction to Logic used the word "matrix" synonymously with the notion of truth table as used in mathematical logic.^[119]

See also

• Mathematics portal

• List of named matrices
• Algebraic multiplicity – Multiplicity of an eigenvalue as a root of the characteristic polynomial
• Geometric multiplicity – Dimension of the eigenspace associated with an eigenvalue
• Gram–Schmidt process – Orthonormalization of a set of vectors
• Irregular matrix
• Matrix calculus – Specialized notation for multivariable calculus
• Matrix function – Function that maps matrices to matricesPages displaying short descriptions of redirect targets
• Matrix multiplication algorithm
• Tensor — A generalization of matrices with any number of indices
• Bohemian matrices – Set of matrices
• Category of matrices — The algebraic structure formed by matrices and their multiplication

Notes

1. However, in the case of adjacency matrices, matrix multiplication or a variant of it allows the simultaneous computation of the number of paths between any two vertices, and of the shortest length of a path between two vertices.
2. Lang 2002
3. Fraleigh (1976, p. 209)
4. Nering (1970, p. 37)
5. Weisstein, Eric W. "Matrix". mathworld.wolfram.com. Retrieved 2020-08-19.
6. Oualline 2003, Ch. 5
7. Pop; Furdui (2017). Square Matrices of Order 2. Springer International Publishing. ISBN 978-3-319-54938-5.
8. Brown 1991, Definition I.2.1 (addition), Definition I.2.4 (scalar multiplication), and Definition I.2.33 (transpose)
9. Brown 1991, Theorem I.2.6
10. "How to Multiply Matrices". www.mathsisfun.com. Retrieved 2020-08-19.
11. Brown 1991, Definition I.2.20
12. Brown 1991, Theorem I.2.24
13. Horn & Johnson 1985, Ch. 4 and 5
14. Bronson (1970, p. 16)
15. Kreyszig (1972, p. 220)
16. Protter & Morrey (1970, p. 869)
17. Kreyszig (1972, pp. 241, 244)
18. Schneider, Hans; Barker, George Phillip (2012), Matrices and Linear Algebra, Dover Books on Mathematics, Courier Dover Corporation, p. 251, ISBN 978-0-486-13930-2.
19. Perlis, Sam (1991), Theory of Matrices, Dover books on advanced mathematics, Courier Dover Corporation, p. 103, ISBN 978-0-486-66810-9.
20. Anton, Howard (2010), Elementary Linear Algebra (10th ed.), John Wiley & Sons, p. 414, ISBN 978-0-470-45821-1.
21. Horn, Roger A.; Johnson, Charles R. (2012), Matrix Analysis (2nd ed.), Cambridge University Press, p. 17, ISBN 978-0-521-83940-2.
22. Brown 1991, I.2.21 and 22
23. Greub 1975, Section III.2
24. Brown 1991, Definition II.3.3
25. Greub 1975, Section III.1
26. Brown 1991, Theorem II.3.22
27. Horn & Johnson 1985, Theorem 2.5.6
28. Brown 1991, Definition I.2.28
29. Brown 1991, Definition I.5.13
30. Horn & Johnson 1985, Chapter 7
31. Horn & Johnson 1985, Theorem 7.2.1
32. Horn & Johnson 1985, Example 4.0.6, p. 169
33. "Matrix | mathematics". Encyclopedia Britannica. Retrieved 2020-08-19.
34. Brown 1991, Definition III.2.1
35. Brown 1991, Theorem III.2.12
36. Brown 1991, Corollary III.2.16
37. Mirsky 1990, Theorem 1.4.1
38. Brown 1991, Theorem III.3.18
39. Eigen means "own" in German and in Dutch.
40. Brown 1991, Definition III.4.1
41. Brown 1991, Definition III.4.9
42. Brown 1991, Corollary III.4.10
43. Householder 1975, Ch. 7
44. Bau III & Trefethen 1997
45. Golub & Van Loan 1996, Algorithm 1.3.1
46. Golub & Van Loan 1996, Chapters 9 and 10, esp. section 10.2
47. Golub & Van Loan 1996, Chapter 2.3
48. Grcar, Joseph F. (2011-01-01). "John von Neumann's Analysis of Gaussian Elimination and the Origins of Modern Numerical Analysis". SIAM Review. 53 (4): 607–682. doi:10.1137/080734716. ISSN 0036-1445.
49. For example, Mathematica, see Wolfram 2003, Ch. 3.7
50. Press, Flannery & Teukolsky et al. 1992
51. Stoer & Bulirsch 2002, Section 4.1
52. Horn & Johnson 1985, Theorem 2.5.4
53. Horn & Johnson 1985, Ch. 3.1, 3.2
54. Arnold & Cooke 1992, Sections 14.5, 7, 8
55. Bronson 1989, Ch. 15
56. Coburn 1955, Ch. V
57. Lang 2002, Chapter XIII
58. Lang 2002, XVII.1, p. 643
59. Lang 2002, Proposition XIII.4.16
60. Reichl 2004, Section L.2
61. Greub 1975, Section III.3
62. Greub 1975, Section III.3.13
63. Perrone (2024), pp. 99–100
64. See any standard reference in a group.
65. Additionally, the group must be closed in the general linear group.
66. Baker 2003, Def. 1.30
67. Baker 2003, Theorem 1.2
68. Artin 1991, Chapter 4.5
69. Rowen 2008, Example 19.2, p. 198
70. See any reference in representation theory or group representation.
71. See the item "Matrix" in Itõ, ed. 1987
72. "Not much of matrix theory carries over to infinite-dimensional spaces, and what does is not so useful, but it sometimes helps." Halmos 1982, p. 23, Chapter 5
73. "Empty Matrix: A matrix is empty if either its row or column dimension is zero", Glossary Archived 2009-04-29 at the Wayback Machine, O-Matrix v6 User Guide
74. "A matrix having at least one dimension equal to zero is called an empty matrix", MATLAB Data Structures Archived 2009-12-28 at the Wayback Machine
75. Fudenberg & Tirole 1983, Section 1.1.1
76. Manning 1999, Section 15.3.4
77. Ward 1997, Ch. 2.8
78. Stinson 2005, Ch. 1.1.5 and 1.2.4
79. Association for Computing Machinery 1979, Ch. 7
80. Godsil & Royle 2004, Ch. 8.1
81. Punnen 2002
82. Lang 1987a, Ch. XVI.6
83. Nocedal 2006, Ch. 16
84. Lang 1987a, Ch. XVI.1
85. Lang 1987a, Ch. XVI.5. For a more advanced, and more general statement see Lang 1969, Ch. VI.2
86. Gilbarg & Trudinger 2001
87. Šolin 2005, Ch. 2.5. See also stiffness method.
88. Latouche & Ramaswami 1999
89. Mehata & Srinivasan 1978, Ch. 2.8
90. Healy, Michael (1986), Matrices for Statistics, Oxford University Press, ISBN 978-0-19-850702-4
91. Krzanowski 1988, Ch. 2.2., p. 60
92. Krzanowski 1988, Ch. 4.1
93. Conrey 2007
94. Zabrodin, Brezin & Kazakov et al. 2006
95. Itzykson & Zuber 1980, Ch. 2
96. see Burgess & Moore 2007, section 1.6.3. (SU(3)), section 2.4.3.2. (Kobayashi–Maskawa matrix)
97. Schiff 1968, Ch. 6
98. Bohm 2001, sections II.4 and II.8
99. Weinberg 1995, Ch. 3
100. Wherrett 1987, part II
101. Riley, Hobson & Bence 1997, 7.17
102. Guenther 1990, Ch. 5
103. Shen, Crossley & Lun 1999 cited by Bretscher 2005, p. 1
104. Discrete Mathematics 4th Ed. Dossey, Otto, Spense, Vanden Eynden, Published by Addison Wesley, October 10, 2001 ISBN 978-0-321-07912-1, p. 564-565
105. Needham, Joseph; Wang Ling (1959). Science and Civilisation in China. Vol. III. Cambridge: Cambridge University Press. p. 117. ISBN 978-0-521-05801-8.
106. Discrete Mathematics 4th Ed. Dossey, Otto, Spense, Vanden Eynden, Published by Addison Wesley, October 10, 2001 ISBN 978-0-321-07912-1, p. 564
107. Merriam-Webster dictionary, Merriam-Webster, retrieved April 20, 2009
108. Although many sources state that J. J. Sylvester coined the mathematical term "matrix" in 1848, Sylvester published nothing in 1848. (For proof that Sylvester published nothing in 1848, see J. J. Sylvester with H. F. Baker, ed., The Collected Mathematical Papers of James Joseph Sylvester (Cambridge, England: Cambridge University Press, 1904), vol. 1.) His earliest use of the term "matrix" occurs in 1850 in J. J. Sylvester (1850) "Additions to the articles in the September number of this journal, "On a new class of theorems," and on Pascal's theorem," The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 37: 363-370. From page 369: "For this purpose, we must commence, not with a square, but with an oblong arrangement of terms consisting, suppose, of m lines and n columns. This does not in itself represent a determinant, but is, as it were, a Matrix out of which we may form various systems of determinants ... "
109. The Collected Mathematical Papers of James Joseph Sylvester: 1837–1853, Paper 37, p. 247
110. Phil.Trans. 1858, vol.148, pp.17-37 Math. Papers II 475-496
111. Dieudonné, ed. 1978, Vol. 1, Ch. III, p. 96
112. Knobloch 1994
113. Hawkins 1975
114. Kronecker 1897
115. Weierstrass 1915, pp. 271–286
116. Bôcher 2004
117. Mehra & Rechenberg 1987
118. Whitehead, Alfred North; and Russell, Bertrand (1913) Principia Mathematica to *56, Cambridge at the University Press, Cambridge UK (republished 1962) cf page 162ff.
119. Tarski, Alfred; (1946) Introduction to Logic and the Methodology of Deductive Sciences, Dover Publications, Inc, New York NY, ISBN 0-486-28462-X.

References

• Anton, Howard (1987), Elementary Linear Algebra (5th ed.), New York: Wiley, ISBN 0-471-84819-0
• Arnold, Vladimir I.; Cooke, Roger (1992), Ordinary differential equations, Berlin, DE; New York, NY: Springer-Verlag, ISBN 978-3-540-54813-3
• Artin, Michael (1991), Algebra, Prentice Hall, ISBN 978-0-89871-510-1
• Association for Computing Machinery (1979), Computer Graphics, Tata McGraw–Hill, ISBN 978-0-07-059376-3
• Baker, Andrew J. (2003), Matrix Groups: An Introduction to Lie Group Theory, Berlin, DE; New York, NY: Springer-Verlag, ISBN 978-1-85233-470-3
• Bau III, David; Trefethen, Lloyd N. (1997), Numerical linear algebra, Philadelphia, PA: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-361-9
• Beauregard, Raymond A.; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Co., ISBN 0-395-14017-X
• Bretscher, Otto (2005), Linear Algebra with Applications (3rd ed.), Prentice Hall
• Bronson, Richard (1970), Matrix Methods: An Introduction, New York: Academic Press, LCCN 70097490
• Bronson, Richard (1989), Schaum's outline of theory and problems of matrix operations, New York: McGraw–Hill, ISBN 978-0-07-007978-6
• Brown, William C. (1991), Matrices and vector spaces, New York, NY: Marcel Dekker, ISBN 978-0-8247-8419-5
• Coburn, Nathaniel (1955), Vector and tensor analysis, New York, NY: Macmillan, OCLC 1029828
• Conrey, J. Brian (2007), Ranks of elliptic curves and random matrix theory, Cambridge University Press, ISBN 978-0-521-69964-8
• Fraleigh, John B. (1976), A First Course In Abstract Algebra (2nd ed.), Reading: Addison-Wesley, ISBN 0-201-01984-1
• Fudenberg, Drew; Tirole, Jean (1983), Game Theory, MIT Press
• Gilbarg, David; Trudinger, Neil S. (2001), Elliptic partial differential equations of second order (2nd ed.), Berlin, DE; New York, NY: Springer-Verlag, ISBN 978-3-540-41160-4
• Godsil, Chris; Royle, Gordon (2004), Algebraic Graph Theory, Graduate Texts in Mathematics, vol. 207, Berlin, DE; New York, NY: Springer-Verlag, ISBN 978-0-387-95220-8
• Golub, Gene H.; Van Loan, Charles F. (1996), Matrix Computations (3rd ed.), Johns Hopkins, ISBN 978-0-8018-5414-9
• Greub, Werner Hildbert (1975), Linear algebra, Graduate Texts in Mathematics, Berlin, DE; New York, NY: Springer-Verlag, ISBN 978-0-387-90110-7
• Halmos, Paul Richard (1982), A Hilbert space problem book, Graduate Texts in Mathematics, vol. 19 (2nd ed.), Berlin, DE; New York, NY: Springer-Verlag, ISBN 978-0-387-90685-0, MR 0675952
• Horn, Roger A.; Johnson, Charles R. (1985), Matrix Analysis, Cambridge University Press, ISBN 978-0-521-38632-6
• Householder, Alston S. (1975), The theory of matrices in numerical analysis, New York, NY: Dover Publications, MR 0378371
• Kreyszig, Erwin (1972), Advanced Engineering Mathematics (3rd ed.), New York: Wiley, ISBN 0-471-50728-8.
• Krzanowski, Wojtek J. (1988), Principles of multivariate analysis, Oxford Statistical Science Series, vol. 3, The Clarendon Press Oxford University Press, ISBN 978-0-19-852211-9, MR 0969370
• Itô, Kiyosi, ed. (1987), Encyclopedic dictionary of mathematics. Vol. I-IV (2nd ed.), MIT Press, ISBN 978-0-262-09026-1, MR 0901762
• Lang, Serge (1969), Analysis II, Addison-Wesley
• Lang, Serge (1987a), Calculus of several variables (3rd ed.), Berlin, DE; New York, NY: Springer-Verlag, ISBN 978-0-387-96405-8
• Lang, Serge (1987b), Linear algebra, Berlin, DE; New York, NY: Springer-Verlag, ISBN 978-0-387-96412-6
• Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, vol. 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556
• Latouche, Guy; Ramaswami, Vaidyanathan (1999), Introduction to matrix analytic methods in stochastic modeling (1st ed.), Philadelphia, PA: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-425-8
• Manning, Christopher D.; Schütze, Hinrich (1999), Foundations of statistical natural language processing, MIT Press, ISBN 978-0-262-13360-9
• Mehata, K. M.; Srinivasan, S. K. (1978), Stochastic processes, New York, NY: McGraw–Hill, ISBN 978-0-07-096612-3
• Mirsky, Leonid (1990), An Introduction to Linear Algebra, Courier Dover Publications, ISBN 978-0-486-66434-7
• Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley, LCCN 76-91646
• Nocedal, Jorge; Wright, Stephen J. (2006), Numerical Optimization (2nd ed.), Berlin, DE; New York, NY: Springer-Verlag, p. 449, ISBN 978-0-387-30303-1
• Oualline, Steve (2003), Practical C++ programming, O'Reilly, ISBN 978-0-596-00419-4
• Perrone, Paolo (2024), Starting Category Theory, World Scientific, doi:10.1142/9789811286018_0005, ISBN 978-981-12-8600-1
• Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T. (1992), "LU Decomposition and Its Applications" (PDF), Numerical Recipes in FORTRAN: The Art of Scientific Computing (2nd ed.), Cambridge University Press, pp. 34–42, archived from the original on 2009-09-06{{citation}}: CS1 maint: unfit URL (link)
• Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, LCCN 76087042
• Punnen, Abraham P.; Gutin, Gregory (2002), The traveling salesman problem and its variations, Boston, MA: Kluwer Academic Publishers, ISBN 978-1-4020-0664-7
• Reichl, Linda E. (2004), The transition to chaos: conservative classical systems and quantum manifestations, Berlin, DE; New York, NY: Springer-Verlag, ISBN 978-0-387-98788-0
• Rowen, Louis Halle (2008), Graduate Algebra: noncommutative view, Providence, RI: American Mathematical Society, ISBN 978-0-8218-4153-2
• Šolin, Pavel (2005), Partial Differential Equations and the Finite Element Method, Wiley-Interscience, ISBN 978-0-471-76409-0
• Stinson, Douglas R. (2005), Cryptography, Discrete Mathematics and its Applications, Chapman & Hall/CRC, ISBN 978-1-58488-508-5
• Stoer, Josef; Bulirsch, Roland (2002), Introduction to Numerical Analysis (3rd ed.), Berlin, DE; New York, NY: Springer-Verlag, ISBN 978-0-387-95452-3
• Ward, J. P. (1997), Quaternions and Cayley numbers, Mathematics and its Applications, vol. 403, Dordrecht, NL: Kluwer Academic Publishers Group, doi:10.1007/978-94-011-5768-1, ISBN 978-0-7923-4513-8, MR 1458894
• Wolfram, Stephen (2003), The Mathematica Book (5th ed.), Champaign, IL: Wolfram Media, ISBN 978-1-57955-022-6

Physics references

• Bohm, Arno (2001), Quantum Mechanics: Foundations and Applications, Springer, ISBN 0-387-95330-2
• Burgess, Cliff; Moore, Guy (2007), The Standard Model. A Primer, Cambridge University Press, ISBN 978-0-521-86036-9
• Guenther, Robert D. (1990), Modern Optics, John Wiley, ISBN 0-471-60538-7
• Itzykson, Claude; Zuber, Jean-Bernard (1980), Quantum Field Theory, McGraw–Hill, ISBN 0-07-032071-3
• Riley, Kenneth F.; Hobson, Michael P.; Bence, Stephen J. (1997), Mathematical methods for physics and engineering, Cambridge University Press, ISBN 0-521-55506-X
• Schiff, Leonard I. (1968), Quantum Mechanics (3rd ed.), McGraw–Hill
• Weinberg, Steven (1995), The Quantum Theory of Fields. Volume I: Foundations, Cambridge University Press, ISBN 0-521-55001-7
• Wherrett, Brian S. (1987), Group Theory for Atoms, Molecules and Solids, Prentice–Hall International, ISBN 0-13-365461-3
• Zabrodin, Anton; Brezin, Édouard; Kazakov, Vladimir; Serban, Didina; Wiegmann, Paul (2006), Applications of Random Matrices in Physics (NATO Science Series II: Mathematics, Physics and Chemistry), Berlin, DE; New York, NY: Springer-Verlag, ISBN 978-1-4020-4530-1

Historical references

• A. Cayley A memoir on the theory of matrices. Phil. Trans. 148 1858 17–37; Math. Papers II 475–496
• Bôcher, Maxime (2004), Introduction to higher algebra, New York, NY: Dover Publications, ISBN 978-0-486-49570-5, reprint of the 1907 original edition
• Cayley, Arthur (1889), The collected mathematical papers of Arthur Cayley, vol. I (1841–1853), Cambridge University Press, pp. 123–126
• Dieudonné, Jean, ed. (1978), Abrégé d'histoire des mathématiques 1700-1900, Paris, FR: Hermann
• Hawkins, Thomas (1975), "Cauchy and the spectral theory of matrices", Historia Mathematica, 2: 1–29, doi:10.1016/0315-0860(75)90032-4, ISSN 0315-0860, MR 0469635
• Knobloch, Eberhard (1994), "From Gauss to Weierstrass: determinant theory and its historical evaluations", The intersection of history and mathematics, Science Networks Historical Studies, vol. 15, Basel, Boston, Berlin: Birkhäuser, pp. 51–66, MR 1308079
• Kronecker, Leopold (1897), Hensel, Kurt (ed.), Leopold Kronecker's Werke, Teubner
• Mehra, Jagdish; Rechenberg, Helmut (1987), The Historical Development of Quantum Theory (1st ed.), Berlin, DE; New York, NY: Springer-Verlag, ISBN 978-0-387-96284-9
• Shen, Kangshen; Crossley, John N.; Lun, Anthony Wah-Cheung (1999), Nine Chapters of the Mathematical Art, Companion and Commentary (2nd ed.), Oxford University Press, ISBN 978-0-19-853936-0
• Weierstrass, Karl (1915), Collected works, vol. 3

Further reading

• "Matrix", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• The Matrix Cookbook (PDF), retrieved 24 March 2014
• Brookes, Mike (2005), The Matrix Reference Manual, London: Imperial College, archived from the original on 16 December 2008, retrieved 10 Dec 2008

External links

• MacTutor: Matrices and determinants
• Matrices and Linear Algebra on the Earliest Uses Pages
• Earliest Uses of Symbols for Matrices and Vectors