Método Hartree-Fock

Método en física cuántica.

En física y química computacional , el método Hartree-Fock ( HF ) es un método de aproximación para la determinación de la función de onda y la energía de un sistema cuántico de muchos cuerpos en estado estacionario .

El método Hartree-Fock a menudo supone que la función de onda exacta de N -cuerpos del sistema puede aproximarse mediante un único determinante de Slater (en el caso de que las partículas sean fermiones ) o mediante un único permanente (en el caso de bosones ) de N. orbitales de espín . Al invocar el método variacional , se puede derivar un conjunto de N ecuaciones acopladas para los N orbitales de espín. Una solución de estas ecuaciones produce la función de onda de Hartree-Fock y la energía del sistema. La aproximación de Hartree-Fock es un ejemplo de la teoría del campo medio , ^[1] donde descuidar las fluctuaciones de orden superior en el parámetro de orden permite reemplazar los términos de interacción con términos cuadráticos, obteniendo hamiltonianos exactamente resolubles.

Especialmente en la literatura más antigua, el método Hartree-Fock también se denomina método de campo autoconsistente ( SCF ). Al derivar lo que ahora se llama ecuación de Hartree como una solución aproximada de la ecuación de Schrödinger , Hartree requirió que el campo final calculado a partir de la distribución de carga fuera "autoconsistente" con el campo inicial supuesto. Por tanto, la autoconsistencia era un requisito de la solución. Las soluciones de las ecuaciones no lineales de Hartree-Fock también se comportan como si cada partícula estuviera sujeta al campo medio creado por todas las demás partículas (consulte el operador de Fock a continuación) y, por lo tanto, la terminología continuó. Las ecuaciones se resuelven casi universalmente mediante un método iterativo , aunque el algoritmo de iteración de punto fijo no siempre converge. ^[2] Este esquema de solución no es el único posible y no es una característica esencial del método Hartree-Fock.

El método Hartree-Fock encuentra su aplicación típica en la solución de la ecuación de Schrödinger para átomos, moléculas, nanoestructuras ^[3] y sólidos, pero también ha encontrado un uso generalizado en la física nuclear . (Consulte el método Hartree-Fock-Bogoliubov para una discusión sobre su aplicación en la teoría de la estructura nuclear ). En la teoría de la estructura atómica , los cálculos pueden ser para un espectro con muchos niveles de energía excitados y, en consecuencia, el método Hartree-Fock para átomos supone que la función de onda es una función de estado de configuración única con números cuánticos bien definidos y que el nivel de energía no es necesariamente el estado fundamental .

Tanto para átomos como para moléculas, la solución de Hartree-Fock es el punto de partida central para la mayoría de los métodos que describen con mayor precisión el sistema de muchos electrones.

El resto de este artículo se centrará en aplicaciones de la teoría de estructuras electrónicas adecuadas para moléculas con el átomo como caso especial. La discusión aquí es sólo para el método restringido de Hartree-Fock, donde el átomo o molécula es un sistema de capa cerrada con todos los orbitales (atómicos o moleculares) doblemente ocupados. Los sistemas de capa abierta , donde algunos de los electrones no están apareados, pueden abordarse mediante el método de capa abierta restringido o el método de Hartree-Fock no restringido .

Breve historia

Primeros métodos semiempíricos

El origen del método Hartree-Fock se remonta a finales de la década de 1920, poco después del descubrimiento de la ecuación de Schrödinger en 1926. Los métodos de Douglas Hartree se guiaron por algunos métodos semiempíricos anteriores de principios de la década de 1920 (por E. Fues , RB Lindsay y él mismo) ambientado en la antigua teoría cuántica de Bohr.

En el modelo del átomo de Bohr, la energía de un estado con número cuántico principal n se da en unidades atómicas como . A partir de los espectros atómicos se observó que los niveles de energía de los átomos de muchos electrones se describen bien aplicando una versión modificada de la fórmula de Bohr. Al introducir el defecto cuántico d como parámetro empírico, los niveles de energía de un átomo genérico se aproximaron bien mediante la fórmula , en el sentido de que se podrían reproducir bastante bien los niveles de transiciones observados en la región de rayos X (por ejemplo, ver la discusión empírica y la derivación en la ley de Moseley ). La existencia de un defecto cuántico distinto de cero se atribuyó a la repulsión electrón-electrón, que claramente no existe en el átomo de hidrógeno aislado. Esta repulsión resultó en un blindaje parcial de la carga nuclear desnuda. Estos primeros investigadores introdujeron posteriormente otros potenciales que contenían parámetros empíricos adicionales con la esperanza de reproducir mejor los datos experimentales. ${\displaystyle E=-1/n^{2}}$ ${\displaystyle E=-1/(n+d)^{2}}$

método hartree

En 1927, DR Hartree introdujo un procedimiento, al que llamó método de campo autoconsistente, para calcular funciones de onda y energías aproximadas para átomos e iones. ^[4] Hartree intentó eliminar los parámetros empíricos y resolver la ecuación de Schrödinger de muchos cuerpos independiente del tiempo a partir de principios físicos fundamentales, es decir, ab initio . Su primer método de solución propuesto se conoció como método de Hartree o producto de Hartree . Sin embargo, muchos de los contemporáneos de Hartree no entendieron el razonamiento físico detrás del método Hartree: a muchas personas les parecía que contenía elementos empíricos y su conexión con la solución de la ecuación de Schrödinger de muchos cuerpos no estaba clara. Sin embargo, en 1928 JC Slater y JA Gaunt demostraron de forma independiente que el método Hartree podía formularse sobre una base teórica más sólida aplicando el principio variacional a un ansatz (función de onda de prueba) como producto de funciones de una sola partícula. ^{[5] [6]}

En 1930, Slater y VA Fock señalaron de forma independiente que el método Hartree no respetaba el principio de antisimetría de la función de onda. ^{[7] [8]} El método Hartree utilizó el principio de exclusión de Pauli en su formulación anterior, prohibiendo la presencia de dos electrones en el mismo estado cuántico. Sin embargo, se demostró que esto era fundamentalmente incompleto al descuidar la estadística cuántica .

Hartree-Fock

Una solución a la falta de antisimetría en el método de Hartree llegó cuando se demostró que un determinante de Slater , un determinante de orbitales de una partícula utilizado por primera vez por Heisenberg y Dirac en 1926, satisface trivialmente la propiedad antisimétrica de la solución exacta y, por tanto, es un ansatz adecuado para aplicar el principio variacional . El método Hartree original puede verse entonces como una aproximación al método Hartree-Fock al ignorar el intercambio . El método original de Fock se basaba en gran medida en la teoría de grupos y era demasiado abstracto para que los físicos contemporáneos lo comprendieran e implementaran. En 1935, Hartree reformuló el método para que fuera más adecuado a los efectos del cálculo. ^[9]

El método Hartree-Fock, a pesar de su imagen físicamente más precisa, se utilizó poco hasta la llegada de las computadoras electrónicas en la década de 1950 debido a las demandas computacionales mucho mayores que los primeros métodos de Hartree y los modelos empíricos. ^[10] Inicialmente, tanto el método Hartree como el método Hartree-Fock se aplicaron exclusivamente a átomos, donde la simetría esférica del sistema permitió simplificar enormemente el problema. Estos métodos aproximados se usaron (y se usan) a menudo junto con la aproximación del campo central para imponer la condición de que los electrones en la misma capa tengan la misma parte radial y restringir la solución variacional a una función propia de espín . Aun así, calcular una solución a mano utilizando las ecuaciones de Hartree-Fock para un átomo de tamaño mediano era laborioso; Las moléculas pequeñas requerían recursos computacionales mucho más allá de los que estaban disponibles antes de 1950.

Algoritmo de Hartree-Fock

El método Hartree-Fock se utiliza normalmente para resolver la ecuación de Schrödinger independiente del tiempo para un átomo o molécula multielectrónico como se describe en la aproximación de Born-Oppenheimer . Dado que no se conocen soluciones analíticas para sistemas de muchos electrones (existen soluciones para sistemas de un solo electrón, como los átomos de hidrógeno y el catión de hidrógeno diatómico), el problema se resuelve numéricamente. Debido a las no linealidades introducidas por la aproximación de Hartree-Fock, las ecuaciones se resuelven utilizando un método no lineal como la iteración , lo que da origen al nombre de "método de campo autoconsistente".

Aproximaciones

El método Hartree-Fock realiza cinco simplificaciones importantes para abordar esta tarea:

• Se supone inherentemente la aproximación de Born-Oppenheimer . La función de onda molecular completa es en realidad función de las coordenadas de cada uno de los núcleos, además de las de los electrones.
• Normalmente, los efectos relativistas se ignoran por completo. Se supone que el operador de momento es completamente no relativista.
• Se supone que la solución variacional es una combinación lineal de un número finito de funciones básicas , que generalmente (pero no siempre) se eligen como ortogonales . Se supone que el conjunto de bases finitas es aproximadamente completo .
• Se supone que cada función propia de energía se puede describir mediante un único determinante de Slater , un producto antisimetrizado de funciones de onda de un electrón (es decir, orbitales ).
• La aproximación del campo medio está implícita. Se desprecian los efectos que surgen de las desviaciones de este supuesto. Estos efectos a menudo se utilizan colectivamente como definición del término correlación electrónica . Sin embargo, la etiqueta "correlación electrónica" estrictamente hablando abarca tanto la correlación de Coulomb como la correlación de Fermi, y esta última es un efecto del intercambio de electrones, que se tiene plenamente en cuenta en el método Hartree-Fock. ^{[11] [12]} Dicho en esta terminología, el método sólo ignora la correlación de Coulomb. Sin embargo, este es un defecto importante que explica (entre otros) la incapacidad de Hartree-Fock para capturar la dispersión de Londres . ^[13]

La relajación de las dos últimas aproximaciones da lugar a muchos de los llamados métodos post-Hartree-Fock .

Optimización variacional de orbitales.

Diagrama de flujo algorítmico que ilustra el método Hartree-Fock

El teorema variacional establece que para un operador hamiltoniano independiente del tiempo, cualquier función de onda de prueba tendrá un valor esperado de energía mayor o igual a la verdadera función de onda del estado fundamental correspondiente al hamiltoniano dado. Debido a esto, la energía de Hartree-Fock es un límite superior de la verdadera energía del estado fundamental de una molécula determinada. En el contexto del método Hartree-Fock, la mejor solución posible está en el límite de Hartree-Fock ; es decir, el límite de la energía de Hartree-Fock cuando el conjunto de bases se acerca a su integridad . (El otro es el límite de IC completo , donde las dos últimas aproximaciones de la teoría de Hartree-Fock descritas anteriormente se deshacen por completo. Sólo cuando se alcanzan ambos límites se obtiene la solución exacta, hasta la aproximación de Born-Oppenheimer, obtenido.) La energía de Hartree-Fock es la energía mínima para un solo determinante de Slater.

El punto de partida del método Hartree-Fock es un conjunto de funciones de onda aproximadas de un electrón conocidas como orbitales de espín . Para un cálculo de orbitales atómicos , estos suelen ser los orbitales de un átomo similar al hidrógeno (un átomo con un solo electrón, pero con la carga nuclear adecuada). Para un cálculo cristalino o de orbital molecular , las funciones de onda iniciales aproximadas de un electrón suelen ser una combinación lineal de orbitales atómicos (LCAO).

Los orbitales anteriores sólo representan la presencia de otros electrones de manera promedio. En el método Hartree-Fock, el efecto de otros electrones se tiene en cuenta en el contexto de la teoría del campo medio . Los orbitales se optimizan exigiéndoles que minimicen la energía del determinante de Slater respectivo. Las condiciones de variación resultantes en los orbitales conducen a un nuevo operador de un electrón, el operador de Fock . Como mínimo, los orbitales ocupados son soluciones propias del operador de Fock mediante una transformación unitaria entre ellos. El operador de Fock es un operador hamiltoniano eficaz de un electrón que es la suma de dos términos. El primero es una suma de operadores de energía cinética para cada electrón, la energía de repulsión internuclear y una suma de términos de atracción de Coulómbico nuclear-electrónicos . El segundo son los términos de repulsión de Coulombic entre electrones en una descripción de la teoría del campo medio; una energía de repulsión neta para cada electrón del sistema, que se calcula tratando a todos los demás electrones dentro de la molécula como una distribución suave de carga negativa. Ésta es la principal simplificación inherente al método Hartree-Fock y equivale a la quinta simplificación de la lista anterior.

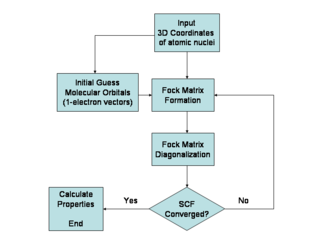
Dado que el operador de Fock depende de los orbitales utilizados para construir la matriz de Fock correspondiente , las funciones propias del operador de Fock son a su vez nuevos orbitales, que pueden usarse para construir un nuevo operador de Fock. De esta manera, los orbitales de Hartree-Fock se optimizan iterativamente hasta que el cambio en la energía electrónica total cae por debajo de un umbral predefinido. De esta forma se calcula un conjunto de orbitales de un electrón autoconsistentes. La función de onda electrónica de Hartree-Fock es entonces el determinante de Slater construido a partir de estos orbitales. Siguiendo los postulados básicos de la mecánica cuántica, la función de onda de Hartree-Fock se puede utilizar para calcular cualquier propiedad química o física deseada dentro del marco del método de Hartree-Fock y las aproximaciones empleadas.

formulación matemática

Derivación

Para derivar Hartree-Fock minimizamos la energía funcional para N electrones

${\displaystyle \delta E[\phi _{k}^{*}(x_{k})]=\delta \left\langle \psi ^{HF}|H^{e}|\psi ^{HF}\right\rangle -\delta \left[\sum _{i=1}^{N}\sum _{j=1}^{N}\lambda _{ij}\left(\left\langle \phi _{i},\phi _{j}\right\rangle -\delta _{ij}\right)\right]{\stackrel {!}{=}}\,0,}$

donde está el hamiltoniano molecular en la aproximación de Born-Oppenheimer, es la función de onda Hartree-Fock del determinante de Slater y el segundo término es la suma sobre un multiplicador de Lagrange y la restricción de que los orbitales de espín del determinante de Slater ${\displaystyle H^{e}}$ ${\displaystyle \psi ^{HF}}$ ${\displaystyle \lambda _{ij}}$ ${\displaystyle \phi _{i}(x_{i})}$

${\displaystyle {\begin{aligned}\psi (\mathbf {x} _{1},\mathbf {x} _{2},\ldots ,\mathbf {x} _{N})&={\frac {1}{\sqrt {N!}}}{\begin{vmatrix}\phi _{1}(\mathbf {x} _{1})&\phi _{2}(\mathbf {x} _{1})&\cdots &\phi _{N}(\mathbf {x} _{1})\\\phi _{1}(\mathbf {x} _{2})&\phi _{2}(\mathbf {x} _{2})&\cdots &\phi _{N}(\mathbf {x} _{2})\\\vdots &\vdots &\ddots &\vdots \\\phi _{1}(\mathbf {x} _{N})&\phi _{2}(\mathbf {x} _{N})&\cdots &\phi _{N}(\mathbf {x} _{N})\end{vmatrix}},\end{aligned}}}$

son ortonormales. Como podemos elegir la base de , elegimos una base en la que la matriz multiplicadora de Lagrange se vuelve diagonal, es decir . Realizando la variación obtenemos ${\displaystyle \phi _{i}(x_{i})}$ ${\displaystyle \lambda _{ij}}$ ${\displaystyle \lambda _{ij}=\epsilon _{i}\delta _{ij}}$

${\displaystyle {\begin{aligned}\delta E[\phi _{k}^{*}(x_{k})]&=\sum _{i=1}^{N}\int {\text{d}}\mathbf {x} _{i}\,h^{1}(\mathbf {x} _{i})\phi _{i}(\mathbf {x} _{i})\delta (\mathbf {x} _{i}-\mathbf {x} _{k})\delta _{ik}\\&+\sum _{i=1}^{N}\sum _{j=1}^{N}\int \mathrm {d} \mathbf {x} _{i}\int {\text{d}}\mathbf {x} _{j}\phi _{j}^{*}(\mathbf {x} _{j}){\frac {1}{|\mathbf {r} _{i}-\mathbf {r} _{j}|}}\phi _{i}(\mathbf {x} _{i})\phi _{j}(\mathbf {x} _{j})\delta (\mathbf {x} _{i}-\mathbf {x} _{k})\delta _{ik}\\&-\sum _{i=1}^{N}\sum _{j=1}^{N}\int {\text{d}}\mathbf {x} _{i}\int {\text{d}}\mathbf {x} _{j}\phi _{j}^{*}(\mathbf {x} _{j}){\frac {1}{|\mathbf {r} _{i}-\mathbf {r} _{j}|}}\phi _{i}(\mathbf {x} _{j})\phi _{j}(\mathbf {x} _{i})\delta (\mathbf {x} _{i}-\mathbf {x} _{k})\delta _{ik}\\&+\sum _{i=1}^{N}\epsilon _{i}\int {\text{d}}\mathbf {x} _{i}\,\phi _{i}(\mathbf {x} _{i})\delta (\mathbf {x} _{i}-\mathbf {x} _{k})\delta _{ik}\\\\&=h^{1}(\mathbf {x} _{k})\phi _{k}(\mathbf {x} _{k})\\&+\sum _{j=1}^{N}\int {\text{d}}\mathbf {x} _{j}\phi _{j}^{*}(\mathbf {x} _{j}){\frac {1}{|\mathbf {r} _{k}-\mathbf {r} _{j}|}}\phi _{k}(\mathbf {x} _{k})\phi _{j}(\mathbf {x} _{j})\\&-\sum _{j=1}^{N}\int {\text{d}}\mathbf {x} _{j}\phi _{j}^{*}(\mathbf {x} _{j}){\frac {1}{|\mathbf {r} _{k}-\mathbf {r} _{j}|}}\phi _{k}(\mathbf {x} _{j})\phi _{j}(\mathbf {x} _{k})\\&+\epsilon _{k}\phi _{k}(\mathbf {x} _{k}).\\\end{aligned}}}$

El factor 1/2 en el hamiltoniano molecular desaparece antes de las integrales dobles debido a la simetría y la regla del producto. Encontramos la ecuación de Fock.

${\displaystyle F(\mathbf {x} _{k})\phi _{k}=\epsilon _{k}\phi _{k}=h^{1}(\mathbf {x} _{k})+J(\mathbf {x} _{k})-K(\mathbf {x} _{k}),}$

donde el operador de Coulomb y el operador de intercambio se definen de la siguiente manera ${\displaystyle J(\mathbf {x} _{k})}$ ${\displaystyle K(\mathbf {x} _{k})}$

${\displaystyle {\begin{aligned}J(\mathbf {x_{k}} )&=\int \mathrm {d} \mathbf {x} _{j}{\frac {\rho (\mathbf {x} _{j})}{|\mathbf {r} _{k}-\mathbf {r} _{j}|}},\\K(\mathbf {x_{k}} )\phi _{k}(\mathbf {x} _{k})&=\sum _{j=1}^{N}\phi _{j}(\mathbf {x} _{k})\int {\text{d}}\mathbf {x} _{j}{\frac {\phi _{j}^{*}(\mathbf {x} _{j})\phi _{k}(\mathbf {x} _{j})}{|\mathbf {r} _{k}-\mathbf {r} _{j}|}}.\\\end{aligned}}}$

El operador de cambio no tiene un análogo clásico y sólo puede definirse como un operador integral.

El operador Fock

Debido a que el término de repulsión electrón-electrón del hamiltoniano molecular involucra las coordenadas de dos electrones diferentes, es necesario reformularlo de manera aproximada. Según esta aproximación (descrita en el algoritmo de Hartree-Fock ), todos los términos del hamiltoniano exacto, excepto el término de repulsión nuclear-nuclear, se reexpresan como la suma de los operadores de un electrón que se detallan a continuación, para átomos o moléculas de capa cerrada ( con dos electrones en cada orbital espacial). ^[14] El "(1)" que sigue a cada símbolo de operador simplemente indica que el operador es de naturaleza 1 electrón.

${\displaystyle {\hat {F}}[\{\phi _{j}\}](1)={\hat {H}}^{\text{core}}(1)+\sum _{j=1}^{N/2}[2{\hat {J}}_{j}(1)-{\hat {K}}_{j}(1)],}$

dónde

${\displaystyle {\hat {F}}[\{\phi _{j}\}](1)}$

es el operador de Fock de un electrón generado por los orbitales , y ${\displaystyle \phi _{j}}$

${\displaystyle {\hat {H}}^{\text{core}}(1)=-{\frac {1}{2}}\nabla _{1}^{2}-\sum _{\alpha }{\frac {Z_{\alpha }}{r_{1\alpha }}}}$

es el hamiltoniano de núcleo de un electrón que incluye energía cinética más atracción a todos los núcleos (el "núcleo") de la molécula, pero omite la interacción con otros electrones. ^[15] También

${\displaystyle {\hat {J}}_{j}(1)}$

es el operador de Coulomb , que define la energía de repulsión electrón-electrón debida a cada uno de los dos electrones en el j -ésimo orbital. ^[14] Finalmente,

${\displaystyle {\hat {K}}_{j}(1)}$

es el operador de intercambio , que define la energía de intercambio de electrones debido a la antisimetría de la función de onda de N -electrones totales. ^[14] Este operador de "intercambio de energía" es simplemente un artefacto del determinante de Slater. Encontrar las funciones de onda de un electrón de Hartree-Fock ahora equivale a resolver la ecuación de función propia ${\displaystyle {\hat {K}}}$

${\displaystyle {\hat {F}}(1)\phi _{i}(1)=\epsilon _{i}\phi _{i}(1),}$

donde hay un conjunto de funciones de onda de un electrón llamadas orbitales moleculares de Hartree-Fock. ${\displaystyle \phi _{i}(1)}$

energía total

Para un átomo o molécula con una configuración electrónica de capa cerrada , la energía total según el método Hartree-Fock es

${\displaystyle E_{HF}=2\sum _{i=1}^{N/2}{\hat {H}}_{ii}^{\text{core}}+\sum _{i=1}^{N/2}\sum _{j=1}^{N/2}[2{\hat {J}}_{ij}-{\hat {K}}_{ij}]+V_{nucl}.}$^[15]

${\displaystyle {\hat {J}}_{ij}}$y son elementos de la matriz de los operadores de Coulomb y de intercambio respectivamente, y es la repulsión electrostática total entre todos los núcleos de la molécula. ${\displaystyle {\hat {K}}_{ij}}$ ${\displaystyle V_{nucl}}$

Combinación lineal de orbitales atómicos.

Normalmente, en los cálculos modernos de Hartree-Fock, las funciones de onda de un electrón se aproximan mediante una combinación lineal de orbitales atómicos . Estos orbitales atómicos se denominan orbitales de tipo Slater . Además, es muy común que los "orbitales atómicos" en uso en realidad estén compuestos por una combinación lineal de uno o más orbitales de tipo gaussiano , en lugar de orbitales de tipo Slater, con el fin de ahorrar grandes cantidades de tiempo de cálculo.

En la práctica se utilizan varios conjuntos de bases , la mayoría de los cuales están compuestos por funciones gaussianas. En algunas aplicaciones, se realiza un método de ortogonalización como el proceso de Gram-Schmidt para producir un conjunto de funciones de base ortogonales. En principio, esto puede ahorrar tiempo de cálculo cuando la computadora resuelve las ecuaciones de Roothaan-Hall al convertir la matriz de superposición de manera efectiva en una matriz de identidad . Sin embargo, en la mayoría de los programas informáticos modernos para cálculos moleculares de Hartree-Fock, este procedimiento no se sigue debido al alto costo numérico de la ortogonalización y a la llegada de algoritmos más eficientes, a menudo escasos, para resolver el problema de valores propios generalizados , de los cuales el Roothaan-Hall las ecuaciones son un ejemplo.

Estabilidad numérica

La estabilidad numérica puede ser un problema con este procedimiento y existen varias formas de combatir esta inestabilidad. Uno de los más básicos y de aplicación general se llama mezcla F o amortiguación. Con la mezcla F, una vez que se calcula la función de onda de un solo electrón, no se utiliza directamente. En su lugar, se utiliza alguna combinación de esa función de onda calculada y las funciones de onda anteriores para ese electrón, siendo la más común una combinación lineal simple de la función de onda calculada e inmediatamente anterior. Una astuta estratagema empleada por Hartree en los cálculos atómicos fue aumentar la carga nuclear, acercando así todos los electrones. A medida que el sistema se estabilizó, se redujo gradualmente a la carga correcta. En los cálculos moleculares a veces se utiliza un enfoque similar: primero se calcula la función de onda para un ion positivo y luego se utilizan estos orbitales como punto de partida para la molécula neutra. Los programas informáticos moleculares modernos de Hartree-Fock utilizan una variedad de métodos para garantizar la convergencia de las ecuaciones de Roothaan-Hall.

Debilidades, extensiones y alternativas.

De las cinco simplificaciones descritas en la sección "Algoritmo de Hartree-Fock", la quinta suele ser la más importante. El descuido de la correlación electrónica puede provocar grandes desviaciones de los resultados experimentales. Se han ideado varios enfoques para esta debilidad, denominados colectivamente métodos post-Hartree-Fock , para incluir la correlación de electrones con la función de onda multielectrónica. Uno de estos enfoques, la teoría de la perturbación de Møller-Plesset , trata la correlación como una perturbación del operador de Fock. Otros amplían la verdadera función de onda multielectrónica en términos de una combinación lineal de determinantes de Slater, como el campo autoconsistente multiconfiguracional , la interacción de configuración , la interacción de configuración cuadrática y el espacio activo completo SCF (CASSCF) . Otros más (como el Monte Carlo cuántico variacional ) modifican la función de onda de Hartree-Fock multiplicándola por una función de correlación (factor "Jastrow"), un término que es explícitamente una función de múltiples electrones que no se pueden descomponer en una sola partícula independiente. funciones.

Una alternativa a los cálculos de Hartree-Fock utilizada en algunos casos es la teoría del funcional de densidad , que trata tanto las energías de intercambio como las de correlación, aunque de forma aproximada. De hecho, es común utilizar cálculos que son un híbrido de los dos métodos; el popular esquema B3LYP es uno de esos métodos funcionales híbridos . Otra opción es utilizar métodos modernos de enlace de valencia .

Paquetes de programas

Para obtener una lista de paquetes de software conocidos por manejar cálculos de Hartree-Fock, particularmente para moléculas y sólidos, consulte la lista de software de química cuántica y física del estado sólido .

Ver también

Referencias

1. Bruus, Henrik; Flensberg, Karsten (2014). Teoría cuántica de muchos cuerpos en física de la materia condensada: una introducción (PDF) (Edición corregida). Oxford Nueva York: Oxford University Press. ISBN 9780198566335.
2. Froese Fischer, Charlotte (1987). "Programa general Hartree-Fock". Comunicaciones de Física Informática . 43 (3): 355–365. Código bibliográfico : 1987CoPhC..43..355F. doi :10.1016/0010-4655(87)90053-1.
3. Abdulsattar, Mudar A. (2012). "Espectros Raman e infrarrojos de nanocristales de superred de SiGe: un estudio de la teoría funcional de la densidad". J. Aplica. Física. 111 (4): 044306–044306–4. Código Bib : 2012JAP...111d4306A. doi : 10.1063/1.3686610 .
4. Hartree, DR (1928). "La mecánica ondulatoria de un átomo con un campo central que no es de Coulomb". Matemáticas. Proc. Camb. Filos. Soc. 24 (1): 111. Código bibliográfico : 1928PCPS...24..111H. doi :10.1017/S0305004100011920. S2CID  121520012.
5. Pizarrero, JC (1928). "El campo autoconsistente y la estructura de los átomos". Física. Apocalipsis 32 (3): 339–348. Código bibliográfico : 1928PhRv...32..339S. doi : 10.1103/PhysRev.32.339.
6. Gaunt, JA (1928). "Una teoría de los campos atómicos de Hartree". Matemáticas. Proc. Camb. Filos. Soc. 24 (2): 328–342. Código Bib : 1928PCPS...24..328G. doi :10.1017/S0305004100015851. S2CID  119685329.
7. Pizarrero, JC (1930). "Nota sobre el método de Hartree". Física. Apocalipsis 35 (2): 210–211. Código bibliográfico : 1930PhRv...35..210S. doi :10.1103/PhysRev.35.210.2.
8. Fock, VA (1930). "Näherungsmethode zur Lösung des quantenmechanischen Mehrkörperproblems". Z. Phys. (en alemán). 61 (1): 126-148. Código Bib : 1930ZPhy...61..126F. doi :10.1007/BF01340294. S2CID  125419115. Fock, VA (1930). ""Campo autoconsistente" mit Austausch für Natrium". Z. Phys. (en alemán). 62 (11): 795–805. Bibcode :1930ZPhy...62..795F. doi :10.1007/BF01330439. S2CID  120921212.
9. Hartree, DR; Hartree, W. (1935). "Campo autoconsistente, con intercambio, por berilio". Proc. R. Soc. Londres. A . 150 (869): 9. Código bibliográfico : 1935RSPSA.150....9H. doi : 10.1098/rspa.1935.0085 .
10. Pizarrero, JC (1951). "Una simplificación del método Hartree-Fock". Revisión física . 81 (3): 385–390. Código bibliográfico : 1951PhRv...81..385S. doi : 10.1103/PhysRev.81.385.
11. Hinchliffe, Alan (2000). Modelado de estructuras moleculares (2ª ed.). Baffins Lane, Chichester, West Sussex PO19 1UD, Inglaterra: John Wiley & Sons Ltd. p. 186.ISBN​ 0-471-48993-X.{{cite book}}: CS1 maint: location (link)
12. Szabo, A.; Ostlund, NS (1996). Química cuántica moderna . Mineola, Nueva York: Dover Publishing. ISBN 0-486-69186-1.
13. AJ Stone (1996), La teoría de las fuerzas intermoleculares , Oxford: Clarendon Press.
14. Levine, Ira N. (1991). Química cuántica (4ª ed.). Acantilados de Englewood, Nueva Jersey: Prentice Hall. pag. 403. ISBN 0-205-12770-3 . 
15. Levine, Ira N. (1991). Química cuántica (4ª ed.). Acantilados de Englewood, Nueva Jersey: Prentice Hall. pag. 402-3. ISBN 0-205-12770-3 . 

Fuentes

• Levine, Ira N. (1991). Química cuántica (4ª ed.). Acantilados de Englewood, Nueva Jersey: Prentice Hall. págs. 455–544. ISBN 0-205-12770-3.
• Cramer, Christopher J. (2002). Fundamentos de la química computacional . Chichester: John Wiley & Sons, Ltd. págs. ISBN 0-471-48552-7.
• Szabo, A.; Ostlund, NS (1996). Química cuántica moderna . Mineola, Nueva York: Dover Publishing. ISBN 0-486-69186-1.

enlaces externos

• La mecánica ondulatoria de un átomo con un campo central no de Coulomb. Parte II. Algunos resultados y discusión por DR Hartree , Mathematical Proceedings of the Cambridge Philosophical Society, volumen 24, 111-132, enero de 1928
• Introducción a la teoría de orbitales moleculares de Hartree-Fock por C. David Sherrill (junio de 2000)
• Teoría del campo medio: Hartree-Fock y BCS en E. Pavarini, E. Koch, J. van den Brink y G. Sawatzky: Materiales cuánticos: experimentos y teoría, Jülich 2016, ISBN 978-3-95806-159-0