Comprender la estructura del núcleo atómico es uno de los desafíos centrales de la física nuclear .
El modelo de cúmulos describe el núcleo como una colección de grupos de protones y neutrones (por ejemplo, partículas alfa ) de tipo molecular con uno o más neutrones de valencia que ocupan orbitales moleculares. [1] [2] [3] [4]
El modelo de gota líquida es uno de los primeros modelos de estructura nuclear , propuesto por Carl Friedrich von Weizsäcker en 1935. [5] Describe el núcleo como un fluido semiclásico formado por neutrones y protones , con una fuerza electrostática repulsiva interna proporcional al número de protones. La naturaleza mecánica cuántica de estas partículas aparece a través del principio de exclusión de Pauli , que establece que no pueden existir dos nucleones del mismo tipo en el mismo estado . Por tanto, el fluido es en realidad lo que se conoce como líquido de Fermi . En este modelo, la energía de enlace de un núcleo con protones y neutrones viene dada por
donde es el número total de nucleones ( número másico ). Los términos proporcionales a y representan el volumen y la energía superficial de la gota de líquido, el término proporcional a representa la energía electrostática, el término proporcional a representa el principio de exclusión de Pauli y el último término es el término de apareamiento, que reduce la energía para números pares de protones o neutrones. Los coeficientes y la fuerza del término de apareamiento pueden estimarse teóricamente o ajustarse a los datos. Este modelo simple reproduce las características principales de la energía de enlace de los núcleos.
La suposición de que el núcleo es una gota de líquido de Fermi todavía se utiliza ampliamente en la forma del Modelo de Gotas de Rango Finito (FRDM), debido a la posible buena reproducción de la energía de enlace nuclear en todo el diagrama, con la precisión necesaria para las predicciones de núcleos desconocidos. [6]
La expresión "modelo de capas" es ambigua, ya que se refiere a dos elementos diferentes. Anteriormente se utilizaba para describir la existencia de capas de nucleones según un enfoque más cercano a lo que ahora se denomina teoría del campo medio. En la actualidad, se refiere a un formalismo análogo al formalismo de interacción de configuración utilizado en química cuántica .
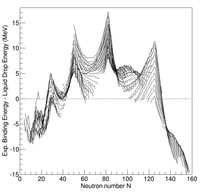
Las mediciones sistemáticas de la energía de enlace de los núcleos atómicos muestran desviaciones sistemáticas con respecto a las estimadas a partir del modelo de la gota líquida. En particular, algunos núcleos que tienen ciertos valores para el número de protones y/o neutrones están unidos más fuertemente que lo previsto por el modelo de la gota líquida. Estos núcleos se denominan " mágicos simples/doblemente mágicos ". Esta observación llevó a los científicos a suponer la existencia de una estructura de capas de nucleones (protones y neutrones) dentro del núcleo, como la de los electrones dentro de los átomos.
En efecto, los nucleones son objetos cuánticos . En sentido estricto, no se debería hablar de energías de nucleones individuales, porque todos ellos están correlacionados entre sí. Sin embargo, como aproximación, se puede imaginar un núcleo medio, dentro del cual los nucleones se propagan individualmente. Debido a su carácter cuántico, sólo pueden ocupar niveles discretos de energía . Estos niveles no están distribuidos de manera uniforme; algunos intervalos de energía están abarrotados y otros están vacíos, lo que genera una brecha en las posibles energías. Una capa es un conjunto de niveles separados de los demás por un amplio espacio vacío.
Los niveles de energía se obtienen resolviendo la ecuación de Schrödinger para un único nucleón que se mueve en el potencial medio generado por todos los demás nucleones. Cada nivel puede estar ocupado por un nucleón o vacío. Algunos niveles admiten varios estados cuánticos diferentes con la misma energía; se dice que son degenerados . Esto ocurre en particular si el núcleo medio presenta una cierta simetría , como una forma esférica.
El concepto de capas permite entender por qué algunos núcleos están más fuertemente unidos que otros. Esto se debe a que dos nucleones del mismo tipo no pueden estar en el mismo estado ( principio de exclusión de Pauli ). Werner Heisenberg extendió el principio de exclusión de Pauli a los nucleones, mediante la introducción del concepto de isoespín. [7] Se cree que los nucleones están compuestos de dos tipos de partículas, el neutrón y el protón, que se diferencian por su propiedad intrínseca, asociada a su número cuántico de isoespín. Este concepto permite explicar el estado ligado del deuterio , en el que el protón y el neutrón pueden acoplar su espín e isoespín de dos maneras diferentes. Por lo tanto, el estado de menor energía del núcleo es aquel en el que los nucleones llenan todos los niveles de energía desde abajo hasta algún nivel. Los núcleos que exhiben un número impar de protones o neutrones están menos ligados que los núcleos con un número par. Un núcleo con capas completas es excepcionalmente estable, como se explicará.
Al igual que sucede con los electrones en el modelo de capas electrónicas , los protones de la capa más externa están relativamente poco unidos al núcleo si solo hay unos pocos protones en esa capa, porque están más alejados del centro del núcleo. Por lo tanto, los núcleos que tienen una capa externa de protones completa estarán más fuertemente unidos y tendrán una energía de enlace más alta que otros núcleos con un número total similar de protones. Esto también es cierto para los neutrones.
Además, la energía necesaria para excitar el núcleo (es decir, mover un nucleón a un nivel superior, previamente desocupado) es excepcionalmente alta en tales núcleos. Siempre que este nivel desocupado sea el siguiente después de una capa llena, la única forma de excitar el núcleo es elevar un nucleón a través del espacio , gastando así una gran cantidad de energía. De lo contrario, si el nivel de energía ocupado más alto se encuentra en una capa parcialmente llena, se requiere mucha menos energía para elevar un nucleón a un estado superior en la misma capa.
Se espera que se produzca cierta evolución de la estructura de capas observada en los núcleos estables a partir del valle de estabilidad . Por ejemplo, las observaciones de isótopos inestables han mostrado un desplazamiento e incluso una reordenación de los niveles de partículas individuales que componen la estructura de capas. [8] Esto a veces se observa como la creación de una isla de inversión o en la reducción de las brechas de energía de excitación por encima de los números mágicos tradicionales.
Para dar un marco conceptual preciso al modelo de shell se plantean algunas hipótesis básicas:
El proceso general utilizado en los cálculos del modelo de capas es el siguiente. Primero se define un hamiltoniano para el núcleo. Por lo general, para fines prácticos de cálculo, solo se tienen en cuenta en esta definición los términos de uno y dos cuerpos. La interacción es una teoría efectiva : contiene parámetros libres que deben ajustarse a los datos experimentales.
El siguiente paso consiste en definir una base de estados de partícula única, es decir, un conjunto de funciones de onda que describen todos los estados posibles de los nucleones. La mayoría de las veces, esta base se obtiene mediante un cálculo de Hartree-Fock . Con este conjunto de estados de partícula única, se construyen los determinantes de Slater , es decir, funciones de onda para Z variables de protones o N variables de neutrones, que son productos antisimetrizados de funciones de onda de partícula única (antisimetrizado significa que bajo intercambio de variables para cualquier par de nucleones, la función de onda solo cambia de signo).
En principio, el número de estados cuánticos disponibles para un único nucleón a una energía finita es finito, digamos n . El número de nucleones en el núcleo debe ser menor que el número de estados disponibles, de lo contrario el núcleo no puede contener todos sus nucleones. Por lo tanto, existen varias formas de elegir Z (o N ) estados entre los n posibles. En matemáticas combinatorias , el número de opciones de Z objetos entre n es el coeficiente binomial CZn
Si n es mucho mayor que Z (o N ), este aumenta aproximadamente como n Z. En la práctica, este número se vuelve tan grande que todo cálculo es imposible para A = N + Z mayor que 8.
Para obviar esta dificultad, el espacio de posibles estados de partículas individuales se divide en núcleo y valencia, por analogía con la química (ver electrón de núcleo y electrón de valencia ). El núcleo es un conjunto de partículas individuales que se supone que son inactivas, en el sentido de que son los estados de energía más bajos bien ligados, y que no hay necesidad de reexaminar su situación. No aparecen en los determinantes de Slater, al contrario de los estados en el espacio de valencia, que es el espacio de todos los estados de partículas individuales que no están en el núcleo , pero posiblemente se consideren en la elección de la construcción de la función de onda de ( Z -) N -cuerpos. El conjunto de todos los posibles determinantes de Slater en el espacio de valencia define una base para los estados de ( Z -) N -cuerpos.
El último paso consiste en calcular la matriz del hamiltoniano dentro de esta base y diagonalizarla. A pesar de la reducción de la dimensión de la base debido a la fijación del núcleo, las matrices a diagonalizar alcanzan fácilmente dimensiones del orden de 10 9 y exigen técnicas de diagonalización específicas.
Los cálculos del modelo de capas se ajustan en general de manera excelente a los datos experimentales. Sin embargo, dependen en gran medida de dos factores principales:
La interacción entre nucleones , que es consecuencia de interacciones fuertes y une a los nucleones dentro del núcleo, exhibe el comportamiento peculiar de tener un rango finito: se desvanece cuando la distancia entre dos nucleones se vuelve demasiado grande; es atractiva en un rango medio y repulsiva en un rango muy pequeño. Esta última propiedad se correlaciona con el principio de exclusión de Pauli según el cual dos fermiones (los nucleones son fermiones) no pueden estar en el mismo estado cuántico. Esto da como resultado un camino libre medio muy grande predicho para un nucleón dentro del núcleo. [9]
La idea principal del enfoque de partículas independientes es que un nucleón se mueve dentro de un cierto pozo de potencial (que lo mantiene unido al núcleo) independientemente de los otros nucleones. Esto equivale a reemplazar un problema de N cuerpos ( N partículas que interactúan) por N problemas de un solo cuerpo. Esta simplificación esencial del problema es la piedra angular de las teorías de campo medio. Estas también se utilizan ampliamente en física atómica , donde los electrones se mueven en un campo medio debido al núcleo central y la propia nube de electrones.
El modelo de partículas independientes y las teorías de campo medio (veremos que existen varias variantes) tienen un gran éxito en la descripción de las propiedades del núcleo a partir de una interacción efectiva o un potencial efectivo, por lo que son una parte básica de la teoría del núcleo atómico. También hay que destacar que son bastante modulares, en el sentido de que es bastante fácil extender el modelo para introducir efectos como el apareamiento nuclear o movimientos colectivos del nucleón como la rotación o la vibración , añadiendo los términos de energía correspondientes en el formalismo. Esto implica que en muchas representaciones, el campo medio es sólo un punto de partida para una descripción más completa que introduce correlaciones que reproducen propiedades como las excitaciones colectivas y la transferencia de nucleones. [10] [11]
Una gran parte de las dificultades prácticas que se presentan en las teorías de campos medios es la definición (o cálculo) del potencial del propio campo medio. Se pueden distinguir, a grandes rasgos, dos enfoques:
En el caso de los métodos Hartree-Fock, el problema no es encontrar la función matemática que describa mejor el potencial nuclear, sino la que describa mejor la interacción nucleón-nucleón. De hecho, a diferencia de la física atómica , donde la interacción es conocida (es la interacción de Coulomb ), la interacción nucleón-nucleón dentro del núcleo no se conoce analíticamente.
Existen dos razones principales para este hecho. En primer lugar, la interacción fuerte actúa esencialmente entre los quarks que forman los nucleones. La interacción nucleón-nucleón en el vacío es una mera consecuencia de la interacción quark-quark. Si bien esta última se entiende bien en el marco del Modelo Estándar a altas energías, es mucho más complicada a bajas energías debido al confinamiento de color y la libertad asintótica . Por lo tanto, aún no existe una teoría fundamental que permita deducir la interacción nucleón-nucleón a partir de la interacción quark-quark. Además, incluso si se resolviera este problema, seguiría habiendo una gran diferencia entre el caso ideal (y conceptualmente más simple) de dos nucleones interactuando en el vacío y el de estos nucleones interactuando en la materia nuclear. Para ir más allá, fue necesario inventar el concepto de interacción efectiva. Esta última es básicamente una función matemática con varios parámetros arbitrarios, que se ajustan para que coincidan con los datos experimentales.
La mayoría de las interacciones modernas son de rango cero, por lo que actúan solo cuando los dos nucleones están en contacto, como lo introdujo Tony Skyrme . [12] En un artículo seminal [13] de Dominique Vautherin y David M. Brink se demostró que una fuerza de Skyrme que depende de la densidad puede reproducir propiedades básicas de los núcleos atómicos. Otra interacción comúnmente utilizada es la fuerza de Gogny de rango finito, [14]
En el enfoque de Hartree-Fock del problema de n cuerpos , el punto de partida es un hamiltoniano que contiene n términos de energía cinética y términos potenciales. Como se mencionó anteriormente, una de las hipótesis de la teoría del campo medio es que solo se debe tener en cuenta la interacción de dos cuerpos. El término potencial del hamiltoniano representa todas las interacciones posibles de dos cuerpos en el conjunto de n fermiones . Es la primera hipótesis.
El segundo paso consiste en suponer que la función de onda del sistema puede escribirse como determinante de Slater de los orbitales de espín de una partícula . Esta afirmación es la traducción matemática del modelo de partícula independiente. Ésta es la segunda hipótesis.
Ahora queda determinar los componentes de este determinante de Slater, es decir, las funciones de onda individuales de los nucleones. Para ello, se supone que la función de onda total (el determinante de Slater) es tal que la energía es mínima. Ésta es la tercera hipótesis.
Técnicamente, esto significa que hay que calcular el valor medio del hamiltoniano de dos cuerpos (conocido) sobre el determinante de Slater (desconocido) e imponer que su variación matemática se anule. Esto conduce a un conjunto de ecuaciones en las que las incógnitas son las funciones de onda individuales: las ecuaciones de Hartree-Fock. Al resolver estas ecuaciones se obtienen las funciones de onda y los niveles de energía individuales de los nucleones y, por lo tanto, la energía total del núcleo y su función de onda.
Esta breve descripción del método Hartree-Fock explica por qué también se lo denomina método variacional . Al comienzo del cálculo, la energía total es una "función de las funciones de onda individuales" (un denominado funcional), y luego se hace todo lo posible para optimizar la elección de estas funciones de onda de modo que la funcional tenga un mínimo, ojalá absoluto y no solo local. Para ser más precisos, debe mencionarse que la energía es una funcional de la densidad , definida como la suma de las funciones de onda al cuadrado individuales. El método Hartree-Fock también se utiliza en física atómica y física de la materia condensada como teoría del funcional de la densidad, DFT.
El proceso de resolución de las ecuaciones de Hartree-Fock sólo puede ser iterativo, ya que se trata de una ecuación de Schrödinger en la que el potencial depende de la densidad , es decir, precisamente de las funciones de onda que se quieren determinar. En la práctica, el algoritmo se inicia con un conjunto de funciones de onda individuales bastante razonables (en general, las funciones propias de un oscilador armónico ). Estas permiten calcular la densidad y, a partir de ella, el potencial de Hartree-Fock. Una vez hecho esto, se resuelve de nuevo la ecuación de Schrödinger, y así sucesivamente. El cálculo se detiene (se alcanza la convergencia) cuando la diferencia entre las funciones de onda, o niveles de energía, para dos iteraciones sucesivas es inferior a un valor fijo. Entonces, el potencial de campo medio está completamente determinado y las ecuaciones de Hartree-Fock se convierten en ecuaciones de Schrödinger estándar. El hamiltoniano correspondiente se denomina entonces hamiltoniano de Hartree-Fock.
Los modelos relativistas del núcleo , que surgieron en los años 1970 con los trabajos de John Dirk Walecka sobre hadrodinámica cuántica , fueron perfeccionados hacia finales de los años 1980 por P. Ring y colaboradores. El punto de partida de estos enfoques es la teoría cuántica de campos relativista . En este contexto, las interacciones entre nucleones se producen mediante el intercambio de partículas virtuales llamadas mesones . La idea es, en un primer paso, construir un lagrangiano que contenga estos términos de interacción. En segundo lugar, mediante una aplicación del principio de mínima acción , se obtiene un conjunto de ecuaciones de movimiento. Las partículas reales (aquí los nucleones) obedecen a la ecuación de Dirac , mientras que las virtuales (aquí los mesones) obedecen a las ecuaciones de Klein-Gordon .
En vista de la naturaleza no perturbativa de la interacción fuerte, y también porque la forma potencial exacta de esta interacción entre grupos de nucleones es relativamente poco conocida, el uso de tal enfoque en el caso de núcleos atómicos requiere aproximaciones drásticas. La simplificación principal consiste en reemplazar en las ecuaciones todos los términos de cuerpo (que son operadores en el sentido matemático) por su valor medio (que son funciones ). De esta manera, se obtiene un sistema de ecuaciones integro-diferenciales acopladas , que se pueden resolver numéricamente, si no analíticamente.
El modelo de bosones interactuantes (IBM) es un modelo de física nuclear en el que los nucleones se representan como pares, cada uno de ellos actuando como una partícula bosónica, con espín integral de 0, 2 o 4. Esto hace que los cálculos sean factibles para núcleos más grandes. Hay varias ramas de este modelo: en una de ellas (IBM-1) se pueden agrupar todos los tipos de nucleones en pares, en otras (por ejemplo, IBM-2) se consideran los protones y neutrones en pares por separado.
Uno de los puntos focales de toda la física es la simetría . La interacción nucleón-nucleón y todas las interacciones efectivas utilizadas en la práctica tienen ciertas simetrías. Son invariantes por traslación (cambio del marco de referencia de modo que las direcciones no se alteren), por rotación (giro del marco de referencia alrededor de algún eje) o por paridad (cambio del sentido de los ejes) en el sentido de que la interacción no cambia bajo ninguna de estas operaciones. Sin embargo, en el enfoque de Hartree-Fock, pueden aparecer soluciones que no son invariantes bajo tal simetría. Se habla entonces de ruptura espontánea de la simetría .
Cualitativamente, estas rupturas espontáneas de simetría pueden explicarse de la siguiente manera: en la teoría del campo medio, el núcleo se describe como un conjunto de partículas independientes. La mayoría de las correlaciones adicionales entre nucleones que no entran en el campo medio se desprecian. Sin embargo, pueden aparecer por una ruptura de la simetría del hamiltoniano del campo medio, que es solo aproximada. Si la densidad utilizada para iniciar las iteraciones del proceso Hartree-Fock rompe ciertas simetrías, el hamiltoniano Hartree-Fock final puede romper estas simetrías, si es ventajoso mantenerlas rotas desde el punto de vista de la energía total.
También puede converger hacia una solución simétrica. En cualquier caso, si la solución final rompe la simetría, por ejemplo, la simetría rotacional, de modo que el núcleo no parece esférico sino elíptico, todas las configuraciones deducidas de este núcleo deformado por una rotación son igualmente buenas soluciones para el problema de Hartree-Fock. El estado fundamental del núcleo es entonces degenerado .
Un fenómeno similar ocurre con el apareamiento nuclear, que viola la conservación del número de bariones (ver más abajo).
La extensión más común de la teoría del campo medio es el apareamiento nuclear. Los núcleos con un número par de nucleones están sistemáticamente más ligados que aquellos con un número impar. Esto implica que cada nucleón se une a otro para formar un par, por lo que el sistema no puede describirse como partículas independientes sujetas a un campo medio común. Cuando el núcleo tiene un número par de protones y neutrones, cada uno de ellos encuentra un compañero. Para excitar un sistema de este tipo, se debe utilizar al menos una energía tal que rompa un par. Por el contrario, en el caso de un número impar de protones o neutrones, existe un nucleón desapareado, que necesita menos energía para ser excitado.
Este fenómeno es estrechamente análogo al de la superconductividad de tipo 1 en la física del estado sólido. La primera descripción teórica del apareamiento nuclear fue propuesta a finales de la década de 1950 por Aage Bohr , Ben Mottelson y David Pines (lo que contribuyó a la recepción del Premio Nobel de Física en 1975 por Bohr y Mottelson). [15] Era cercana a la teoría BCS de Bardeen, Cooper y Schrieffer, que explica la superconductividad del metal. Teóricamente, el fenómeno de apareamiento descrito por la teoría BCS se combina con la teoría del campo medio: los nucleones están sujetos tanto al potencial de campo medio como a la interacción de apareamiento.
El método Hartree–Fock–Bogolyubov (HFB) es un enfoque más sofisticado, [16] que permite considerar las interacciones de emparejamiento y de campo medio de manera uniforme y en igualdad de condiciones. El HFB es ahora el estándar de facto en el tratamiento de campo medio de los sistemas nucleares.
La peculiaridad de los métodos de campo medio es el cálculo de la propiedad nuclear mediante la ruptura explícita de la simetría . El cálculo del campo medio con métodos autoconsistentes (por ejemplo, Hartree-Fock) rompe la simetría rotacional, y el cálculo de la propiedad de emparejamiento rompe el número de partículas.
Se han desarrollado varias técnicas para restaurar la simetría mediante la proyección de buenos números cuánticos. [17]
Los métodos de campo medio (que eventualmente consideran la restauración de la simetría) son una buena aproximación para el estado fundamental del sistema, incluso postulando un sistema de partículas independientes. Las correcciones de orden superior consideran el hecho de que las partículas interactúan entre sí mediante la correlación. Estas correlaciones se pueden introducir teniendo en cuenta el acoplamiento de los grados de libertad de las partículas independientes y la excitación colectiva de baja energía de los sistemas con un número par de protones y neutrones.
De esta manera, los estados excitados pueden reproducirse mediante aproximación de fase aleatoria (RPA), y eventualmente también calculando consistentemente correcciones al estado fundamental (por ejemplo, mediante la teoría de campos nucleares [11] ).