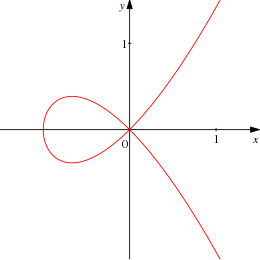Curva cúbica plana

En matemáticas, una curva cúbica plana es una curva algebraica bidimensional C definida por una ecuación cúbica[1]​ aplicada sobre un sistema de coordenadas homogéneas x:y:z para el plano proyectivo; o la versión no homogénea para el espacio afín, determinada mediante el establecimiento de la condición de que z = 1 en dicha ecuación.

Una curva cúbica puede tener un punto singular, en cuyo caso tiene una parametrización en términos de una recta proyectiva.

Los puntos reales de una cúbica proyectiva no singular se localizan en uno o dos 'óvalos'.

Uno de estos óvalos cruza cada recta proyectiva real y, por lo tanto, nunca está delimitado cuando la cúbica se dibuja en el plano euclidiano, y aparece como una o tres ramas infinitas, que contienen los tres puntos de inflexión reales.

Al igual que con las secciones cónicas, una recta corta este óvalo en, como máximo, dos puntos.

Existen muchas curvas cúbicas que no tienen este punto, por ejemplo, cuando K es el campo de los números racionales.

Supóngase que ABC es un triángulo con longitudes de sus lados a = | BC |, b = | CA |, c = | AB |.

Los ejemplos que se muestran a continuación utilizan dos tipos de coordenadas homogéneas: trilineales y baricéntricas.

Así: Las cúbicas listadas a continuación se pueden definir en términos del conjugado isogonal, denotado por X*, de un punto X que no está en una recta lateral de ABC.

Sea LA el reflejo de la línea XA sobre la bisectriz del ángulo interno del ángulo A; definiéndose LB y LC de forma análoga.

Para gráficos y propiedades, véase K004 en Cúbicas en el Plano Triangular.

Para gráficos y propiedades, véase K005 en Cúbicas en el Plano Triangular.

Para el punto arbitrario X, sean XA, XB, XC las intersecciones de las rectas XA', XB', XC' con las rectas laterales BC, CA, AB, respectivamente.

Para cada valor de x obtendremos un polinomio cúbico en y, por lo que obtendremos 3 resultados, descartando los valores imaginarios o complejos, que estarían en el infinito.