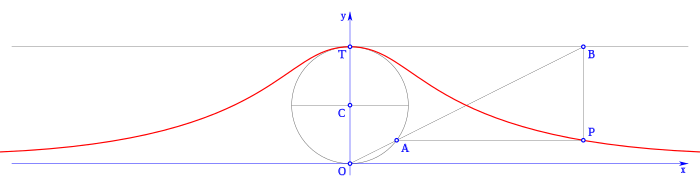
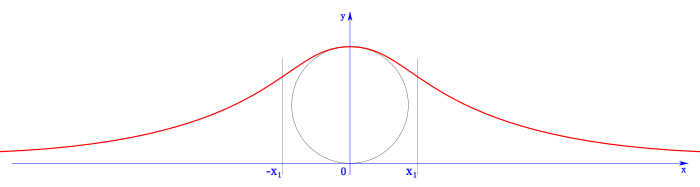
Curva de Agnesi

La asíntota de esta curva es la línea tangente a la circunferencia que pasa por el punto O.Esta curva fue estudiada por Pierre de Fermat en 1630, por Luigi Guido Grandi en 1703 y por Maria Gaetana Agnesi en 1748.Grandi llamó a la curva versoria, del latín vertere, que significa virar o girar; versiera en italiano es un término naval que identifica el cabo o cuerda que hace girar la vela.Los estudios de Agnesi sobre esta curva fueron traducidos al inglés por el profesor de la Universidad de Cambridge John Colson, quien al tener escaso conocimiento del italiano confundió versiera con avversiera, que en italiano significa 'diablesa', 'demonia'.Por eso tradujo el término al inglés como witch (hechicera, bruja), y esta anécdota ha hecho que haya quien guste de llamar "bruja" a esta curva.[2]​[3]​ La curva de Agnesi puede representarse analíticamente como función en el plano xy, tanto en su forma cartesiana y= f(x) como paramétricamente: x= f(t), y= g(t).Para deducir la fórmula cartesiana, se va a tomar el punto O como origen de coordenadas, se localiza T en el lado positivo del eje y, y como radio de la circunferencia se fija el valor a.es el ángulo entre OD y OB, o lo que es lo mismo entre OE y OA, medido en sentido trigonométrico, entonces la curva se define por las ecuaciones: Partiendo, al igual que en la ecuación cartesiana, de: Primero, se despeja la x respecto de, partiendo de: Sabiendo que: se obtien: Elevando esta expresión al cuadrado, resulta: Operando con la expresión: Sabiendo que: se obtiene: Estas ecuaciones dependen del ánguloTambién existe una forma paramétrica más sencilla, eliminando las funciones trigonométricas.Se parte de las ecuaciones: y sabiendo que: se toma el inverso: por la relación del coseno respecto al seno: aplicando la raíz al denominador: operando la fracción: y si se denomina t a: se tiene que: eliminando la raíz: operando: lo que resulta: Con estos resultados y las ecuaciones originales, se obtiene: Con lo que las ecuaciones paramétricas toman la forma: donde t es un parámetro real.El signo de t es el mismo que el de x, así si t es negativo x será negativo, y si t es positivo x será también positivo.Independientemente del valor de t, y siempre tomará valores positivos, para t igual a cero, x valdrá cero é y valdrá 2a.La curva bruja de Agnesi está definida por la función: en el plano cartesiano xy, y donde el parámetro a es el radio de la circunferencia.También puede representarse según el parámetro d, diámetro de la circunferencia, donde d= 2a: Estas dos expresiones son equivalentes, siendo la expresada según el diámetro d, más sencilla al carecer de coeficientes.Las dos se pueden ver al consultar bibliografía, y tienen por representación gráfica: Para estudiar la función de la curva versiera de Agnesi, aquí se toma su expresión cartesiana explícita: donde d es el diámetro de la circunferencia.Se pueden ver las siguientes propiedades: esto es: cuando x tiende a infinito la función se hace cero: y cuando x tiende a menos infinito también se hace cero: Partiendo de la función, se calcula su derivada: Esta derivada solo vale cero cuando x vale cero, por lo tanto puede presentar un extremo relativo para x = 0.Derivando nuevamente se obtiene la segunda derivada de la función: La segunda derivada valdrá cero cuando: Esto es: despejando la x, se obtiene: Lo que resulta: Para los valores: La función presenta puntos de inflexión.