Función continua
Si la función no es continua, se dice que es discontinua.
es aquella cuya gráfica puede dibujarse sin levantar el lápiz del papel (más formalmente su grafo es un conjunto conexo).
Formalmente, una función es continua si se puede conseguir que sus valores varíen arbitrariamente poco a costa de hacer suficientemente pequeñas las distancias entre los argumentos considerados.
Este artículo describe principalmente la continuidad de funciones reales de una variable real, aunque más abajo se describen también las generalizaciones a varias variables, espacios métricos y espacios topológicos.
es continua si la curva que la representa, es decir el conjunto de los puntos
La definición de continuidad en un punto es la siguiente:[2] si: tal que para toda x perteneciente al dominio de la función La anterior definición se puede leer intuitivamente como sigue.
Como todos los puntos del dominio de una sucesión son puntos aislados del mismo, se concluye que toda sucesión es una función continua.
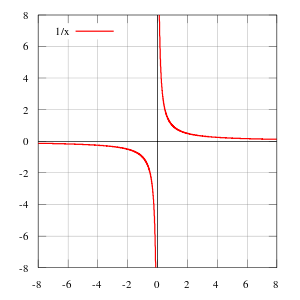
Por ejemplo, la función f(x)=1/x es continua en todos los puntos de su dominio (obsérvese que cero no está en el dominio de la función).
Esto no constituye un problema porque ambas versiones de la definición son equivalentes.
es continua por la primera definición y queremos ver que lo es por la segunda, para cada
Esto implicaría que, dada una función, si no está definida en un punto, ésta no es continua en él, llegando a una situación como la siguiente: La función
Esta definición, no satisfactoria, de continuidad está muy extendida, pero hay que recordar el requisito indispensable para poder hablar de continuidad de que el punto en el que se estudia la continuidad pertenezca al dominio.
Si no está en el dominio, pero es punto de acumulación del mismo, podemos hablar de si puede o no extenderse con continuidad a dicho punto, pero no podemos decir que la función es discontinua en dicho punto (la función extendida sí podría ser discontinua, puesto que al incorporar dicho punto al dominio, tiene sentido plantearse el estudio de la continuidad en él).
Por definición de los límites, esto significa que para todo intervalo abierto J, centrado en y1, existe un intervalo abierto I, centrado en x1, tal que
Si f no es continua en un punto, el teorema cae en falta.
En la gráfica se ve la función seno que es periódica, acotada y continua en todo el dominio real, dado su carácter periódico, con ver uno solo de los ciclos es suficiente para comprobar la continuidad, porque el resto de los ciclos son exactamente iguales.
Esta función no es continua en los enteros, pues los límites a la izquierda y a la derecha son diferentes, pero es continua en los segmentos abiertos (n, n+1) donde es constante.
Estos son algunos de los teoremas más importantes sobre funciones continuas.
pero no derivables en ningún punto (las funciones del movimiento browniano verifican esto con probabilidad 1).
A esta condición se le llama continuidad secuencial en el punto
Hasta ahora hemos definido la continuidad de una función en un punto.
Otra noción, más abstracta, de continuidad es la continuidad entre espacios topológicos, en los que en general no hay definido un concepto de distancia, que se usa en la definición en espacios métricos y, en particular, para funciones reales de variable real, donde se usa la distancia inducida por el valor absoluto.
que harían el papel de los conjuntos abiertos métricos si
Así, para replicar las propiedades de los conjuntos abiertos, a estos subconjuntos se les piden tres propiedades que los abiertos métricos cumplen inmediatamente: que el vacío y el total
Una propiedad fundamental de la continuidad entre espacios métricos es que es equivalente a que la antiimagen de todo abierto (métrico) sea abierta (ver demostración aquí).
En general, como hemos dicho antes, la definición generaliza la continuidad entre dos espacios métricos cualesquiera.
La antiimagen de este abierto por la identidad es él mismo, y no será abierto del espacio de salida, provocando que la aplicación no sea continua.
El término función continua en la parte de la teoría de conjuntos que se refiere a los números ordinales tiene un sentido diferente al referido a las funciones sobre espacios topológicos.
Concretamente una función F definida sobre la clase de los números ordinales
es continua si para cada ordinal límite se cumple la siguiente propiedad: