Hipótesis de Riemann
Leonhard Euler (que murió 43 años antes de que Riemann naciera) demostró que esta serie equivale al producto de Euler: donde el producto infinito se extiende sobre el conjunto de todos los números primos p, y de nuevo converge para los complejos s cuya parte real sea mayor que 1.
La convergencia del producto de Euler muestra que ζ(s) no tiene ceros en esta región, puesto que ninguno de los factores tiene ceros.
Para preservar el sentido de esta hipótesis es necesario prolongar analíticamente la función zeta de Riemann ζ(s) de forma que tenga sentido para cualquier valor de s. En particular se puede expresar mediante la siguiente ecuación funcional: válida para todos los números complejos excepto para s = 1, donde la función tiene un polo.
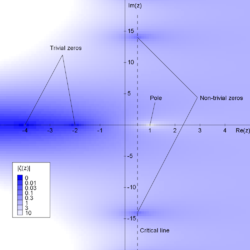
Esta posee ciertos valores, llamados ceros "triviales", para los cuales la función zeta se anula.
Así mismo, existen otros valores complejos s, que cumplen la condición 0 < Re(s) < 1, para los cuales la función zeta también se anula, son los llamados ceros "no triviales".
La conjetura de Riemann hace referencia a estos ceros no triviales afirmando: La parte real de todo cero no trivial de la función zeta de Riemann es 1/2 Por lo tanto los ceros no triviales deberían encontrarse en la línea crítica s = 1/2 + i t, donde t es un número real e i es la unidad imaginaria.
(Si s es un entero par positivo este argumento no se aplica porque los ceros de la función seno son anulados por los polos de la función gamma, ya que toma argumentos enteros negativos).
El valor ζ(0) = -1/2 no viene determinado por la ecuación funcional, sino que es el valor límite de ζ(s) a medida que s se aproxima a cero.
La ecuación funcional también implica que la función zeta no tiene ceros con parte real negativa aparte de los ceros triviales, por lo que todos los ceros no triviales se encuentran en la franja crítica donde s tiene parte real entre 0 y 1.
Riemann mencionó la conjetura en 1859, que sería llamada la hipótesis de Riemann, en su tesis de doctorado Sobre los números primos menores que una magnitud dada, al desarrollar una fórmula explícita para calcular la cantidad de primos menores que x.
Él sabía que los ceros no triviales de la función zeta están distribuidos en torno a la recta s = 1/2 + i t, y sabía también que todos los ceros no triviales debían estar en el rango 0 ≤ Re(s) ≤ 1.
[5] En 1896, Hadamard y de la Vallée-Poussin probaron independientemente, que ningún cero podía estar sobre la recta Re(s) = 1.
Junto con las otras propiedades de los ceros no triviales demostradas por Riemann, esto mostró que todos los ceros no triviales deben estar en el interior de la banda crítica 0 < Re(s) < 1.
Este fue un paso fundamental para las primeras demostraciones del teorema de los números primos.
Cuando se le preguntó qué haría si se despertara habiendo dormido quinientos años, remarcablemente Hilbert contestó que su primera pregunta sería si la hipótesis de Riemann había sido probada.
En 1914, Hardy demostró que existe un número infinito de ceros sobre la recta crítica Re(s) = 1/2.
Sin embargo, todavía era posible que un número infinito (y posiblemente la mayoría) de los ceros no triviales se encontraran en algún otro lugar sobre la banda crítica.
La mayor parte de la comunidad matemática piensa que la conjetura es correcta, aunque otros grandes matemáticos como J. E. Littlewood y Atle Selberg se han mostrado escépticos, si bien el escepticismo de Selberg fue disminuyendo desde sus días de juventud.
[6] La motivación original de Riemann para estudiar la función zeta y sus ceros fue su aparición en su fórmula explícita para la número de primos π(x) menor o igual que un número dado x, que publicó en su artículo de 1859 «Sobre el número de primos menores que una magnitud dada».
La función li que aparece en el primer término es la función integral logarítmica (no compensada) dada por el valor principal de Cauchy de la integral divergente Los términos li(xρ) que involucran los ceros de la función zeta necesitan cierto cuidado en su definición ya que li tiene puntos de ramificación en 0 y 1, y se definen (para x > 1) por continuación analítica en la variable compleja ρ en la región Re(ρ) > 0, es decir, deben considerarse como Ei(ρ log x).
Riemann sabía que los ceros no triviales de la función zeta se distribuían simétricamente alrededor de la recta s = 1/2 + it, y sabía que todos sus ceros no triviales debían encontrarse en el intervalo 0 ≤ Re(s) ≤ 1.
Comprobó que algunos de los ceros estaban en la recta crítica con parte real 1/2 y sugirió que todos lo estaban; ésta es la hipótesis de Riemann.
La función zeta de Riemann tiene una profunda conexión con los números primos y Helge von Koch demostró en 1901 que la hipótesis de Riemann es equivalente al considerable refinamiento del teorema de los números primos: Existe una constante C > 0 tal que para todo x suficientemente grande, donde π(x) es la función contadora de primos y ln(x) es el logaritmo natural de x. Lowell Schoenfeld mostró que se puede tomar C = 1/(8 π) para todo x ≥ 2657.
(zeta) se encuentran en la recta vertical que pasa por
Esta función tiene una profunda conexión con los números primos, donde los ceros de la función zeta y los números primos satisfacen ciertas propiedades de dualidad, conocidas como fórmulas explícitas, que muestran, usando análisis de Fourier, que estos ceros pueden interpretarse como frecuencias armónicas en la distribución de los números primos.
Para valores de x pequeños se había demostrado
No obstante, en 1914 Littlewood empleó la hipótesis de Riemann para mostrar que la desigualdad
se invierte para valores suficientemente grandes de x.
y en 1955, sin usar la hipótesis, mostró que la desigualdad se invierte para algunos
Edwards 1974, Patterson 1988, Borwein/Choi/Rooney/Weirathmueller 2008, Mazur/Stein 2015, Broughan 2017, and Nahin 2021 give mathematical introductions.