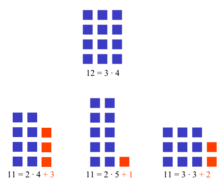
Número primo

Algunos arqueólogos interpretan este hecho como la prueba del conocimiento de los números primos.Hoy en día, empero, los mayores números primos que se encuentran con la ayuda de ordenadores emplean otros algoritmos más rápidos y complejos.Es posible que mucho antes se conociera un caso especial de dicho teorema en China.Se cree que no existen números perfectos impares, pero todavía es una cuestión abierta.Ejemplos de estos algoritmos son el test APRT-CL (desarrollado en 1979 por Adleman, Pomerance y Rumely, con mejoras introducidas por Cohen y Lenstra en 1984), donde se usan los factores de pm-1, donde el exponente m depende del tamaño del número cuya primalidad se desea verificar, el test de primalidad por curvas elípticas (desarrollado en 1986 por S. Goldwasser, J. Kilian y mejorado por A.Desde 1951, el mayor número primo conocido siempre ha sido descubierto con la ayuda de ordenadores.La cuestión acerca de si el número 1 debe o no considerarse primo está basada en la convención.[14]​ Actualmente, la comunidad matemática se inclina por no considerar al 1 en la lista de los números primos.A partir de esta unicidad en la factorización en factores primos se desarrollan otros conceptos muy utilizados en matemáticas, tales como el mínimo común múltiplo, el máximo común divisor y la coprimalidad de dos o más números.Por ejemplo, para conocer el valor de la función φ sobre n=450=2·32·52 basta con calcular Existen infinitos números primos.Euclides realizó la primera demostración alrededor del año 300 a. C. en el libro IX de su obra Elementos.Si se toma como conjunto el de los n primeros números primos, entoncesUn resultado aún más fuerte, y que implica directamente la infinitud de los números primos, fue descubierto por Euler en el siglo xviii.[26]​ Otro resultado es el teorema de Dirichlet, que dice así: En toda progresión aritmética an = a + n·q, donde los enteros positivos a, q ≥ 1 son primos entre sí, existen infinitos términos que son primos.Esto supone que, en una progresión geométrica de primer término entero mayor que 3 y razón igual a 2, entre cada término de la progresión y el siguiente, se tiene al menos un número primo.Consiguió demostrar que, si existía el límite del cociente de aquellas expresiones, este debía ser 1.Por otra parte, en 1901 Von Koch mostró que si la hipótesis de Riemann era cierta, se tenía la siguiente estimación, más precisa:[28]​ Una forma equivalente al teorema de los números primos es que pn, el n-ésimo número primo, queda bien aproximado por nln(n).Por otra parte, la diferencia entre primos consecutivos puede ser tan grande como se quiera.es un número natural arbitrario, entonces el intervalo puede hacerse tan grande como se desee.Por otra parte, a menudo basta con tener una respuesta más rápida con una alta probabilidad (aunque no segura) de ser cierta.Estos tests suelen tomar un número aleatorio llamado "testigo" e introducirlo en una fórmula junto con el número potencialmente primo n. Después de varias iteraciones, se resuelve que n es "definitivamente compuesto" o bien "probablemente primo".Algunos de estos tests no son perfectos: puede haber números compuestos que el test considere "probablemente primos" independientemente del testigo utilizado.Esos números reciben el nombre de pseudoprimos absolutos para ese test.Sin embargo, ambas fórmulas se basan en el cálculo de un factorial, lo que las hace computacionalmente inviables.Cabe subrayar que ningún polinomio, aun en varias variables, devuelve solo valores primos.La segunda igualdad es una consecuencia del teorema fundamental de la aritmética, y muestra que la función zeta está íntimamente relacionada con los números primos.En concreto, la presunción más simple es que los números primos no deberían tener irregularidades significativas en su distribución sin una buena razón.[47]​ Muchas conjeturas tratan sobre si hay infinitos números primos de una determinada forma.La conjetura de Legendre establece que, para cada n natural, existe un número primo entre n2 y (n+1)2., y se dice que dos valoraciones son equivalentes si generan la misma topología.