Número de Fermat

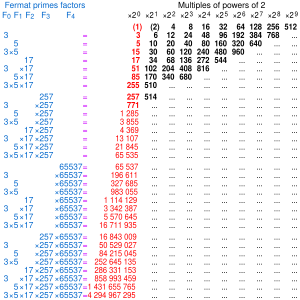
Pierre de Fermat conjeturó que todos los números naturales de la forma con n natural eran números primos (después de todo, los cinco primeros términos, 3 (n=0), 5 (n=1), 17 (n=2), 257 (n=3) y 65537 (n=4) lo son), pero Leonhard Euler probó que no era así en 1732.

El resultado se conoce como Teorema de Gauss-Wantzel: Un entero positivo n tiene la forma anterior si y solo si su totiente φ(n) es una potencia de 2.

Ahora, se multiplica este valor por un número A, que es mayor que la raíz cuadrada de P y es una raíz primitiva módulo P (es decir, no es un residuo cuadrático).

Este método produce solo valores pseudoaleatorios, ya que después de P − 1 repeticiones, la secuencia se repite.

Un multiplicador mal elegido puede hacer que la secuencia se repita antes de P − 1.