Horizonte
Esta línea es en realidad una circunferencia en la superficie de la Tierra centrada en el observador.
Las medidas obtenidas in situ serán en principio referidas al horizonte aparente, y habrá que corregirlas por la refracción atmósférica y por la paralaje geocéntrica para obtener la altura referida al horizonte astronómico.
La palabra horizonte deriva del griego ὁρίζων κύκλος (horízōn kýklos; "límite de la rueda"[1] o "círculo separador"), donde ὁρίζων es del verbo ὁρίζω (horízō) "dividir, separar", que a su vez deriva de ὅρος (hóros) "límite".
Para los observadores cerca del nivel del mar, la diferencia entre este horizonte geométrico (que asume un plano de tierra infinito perfectamente plano) y el horizonte verdadero (que asume una superficie esférica de la Tierra) es imperceptible a simple vista.
Suponiendo a la Tierra como una esfera perfecta (en vez de un esferoide oblato), y sin contar el efecto de la refracción atmosférica, entonces la distancia al horizonte se puede calcular fácilmente.
, y tomando el radio medio de la Tierra como 6371 km, la distancia al horizonte es:[7]
, como sucede con la mayoría de los satélites, la aproximación ya no es válida y se requiere la fórmula exacta.
[10] La parábola muestra un error del 21% de frente al cálculo pitagórico a esta distancia 3,960 millas.
sobre el nivel del mar, y otra persona está en un faro
Entonces, veinte pisos o 70 metros del edificio están ocultos para él por la curvatura de la Tierra.
son casi iguales cuando la altura del objeto es insignificante en comparación con el radio (es decir,
El ángulo cenital máximo visible se produce cuando el rayo es tangente a la superficie de la Tierra; del triángulo OCG en la figura de la derecha, dónde
Si la Tierra fuera un mundo sin aire como la Luna, la luz viajaría horizontalmente y los cálculos anteriores serían precisos.
Esto hace que el aire refracte la luz en diferentes grados, afectando la apariencia del horizonte.
Con condiciones atmosféricas estándares o normalizadas, la diferencia es de aproximadamente el 8%.
Esto cambia el factor de 3,57, en las fórmulas métricas usadas arriba, a aproximadamente 3,86.
En casos extremos, por lo general en primavera, cuando el aire caliente supera el agua fría, la refracción puede permitir que la luz siga la superficie de la Tierra durante cientos de kilómetros.
Las condiciones opuestas ocurren, por ejemplo, en desiertos, donde la superficie es muy caliente, tan caliente, el aire de baja densidad está por debajo del aire más fresco.
Los valores calculados para los efectos de la refracción en condiciones inusuales son por lo tanto aproximados.
[5] Sin embargo, se han hecho intentos para calcularlas con mayor precisión que la aproximación simple descrita anteriormente.
Por lo general el aire es más denso en la superficie, por lo que desde la altura de un observador
Se denomina como "constante de refracción" la relación del radio terrestre
[5][10] Entonces mediante la ecuación anterior de la distancia exacta del horizonte se obtiene que:[10][14]
Un enfoque mucho más simple por Andrew T. Young (2013),[5] que provee esencialmente los mismos resultados que la aproximación de primero orden presentada arriba, utiliza el modelo geométrico pero utiliza un radio de
Para unidades inglesas existe una vieja regla data por R. Langton Cole (1913), donde:[5][21]
Sin embargo, la curvatura aparente es menor que la debida a la refracción de la luz por la atmósfera y el oscurecimiento del horizonte por las altas capas de nubes que reducen la altitud sobre la superficie visual.
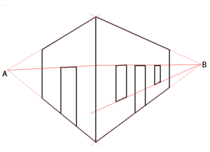
El horizonte es una característica clave del plano pictórico en la ciencia de la perspectiva gráfica.
En su libro Geometry of an Art (2007), Kirsti Andersen describió la evolución del dibujo en perspectiva y la ciencia hasta 1800, señalando que los puntos de fuga no tienen por qué estar en el horizonte.
Stillwell también se aventuró en los fundamentos de las matemáticas en una sección titulada "¿Cuáles son las leyes del álgebra?"
Stillwell afirma A partir de la tercera se toma en cuenta la altura del observador.