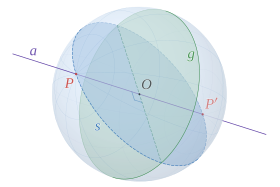
Gran círculo

El más corto de los dos arcos ortodrómicos entre dos puntos distintos de la esfera se denomina arco menor, y es el camino superficial más corto entre ellos.Su longitud de arco es la distancia ortodrómica entre los puntos (la distancia intrínseca en una esfera), y es proporcional a la medida del ángulo central formado por los dos puntos y el centro de la esfera.En la geometría riemanniana este concepto sirve para ilustrar cómo hay espacios donde hay puntos (los antipodales) que admiten más de una geodésica contrastando lo que sucede en espacios euclídeos, en los que por dos puntos elegidos arbitrariamente solo pasa una única geodésica.Si tres puntos de la superficie esférica son unidos por arcos de círculo máximo menores a 180°, la figura obtenida se denomina triángulo esférico.Los lados del polígono así formado se expresan por conveniencia como ángulos cuyo vértice es el centro de la esfera y no por su longitud.< 540° En geografía y cartografía, los círculos máximos que pasan por los polos determinan las líneas de longitud (meridianos).La duración del vuelo a menudo se puede estimar mediante un gran círculo entre dos aeropuertos.Al mismo tiempo, para las aeronaves que se mueven hacia el oeste entre continentes en el hemisferio norte , la ruta óptima se encuentra al norte del gran círculo, respectivamente, para el movimiento hacia el este, las rutas óptimas serán ligeramente hacia el sur.La ruta correspondiente al segmento recto en el mapa será más larga.El hecho es que en tales proyecciones, los círculos grandes no corresponden a líneas rectas.Para demostrar que el arco menor de un círculo máximo es la trayectoria más corta que conecta dos puntos en la superficie de una esfera, se puede utilizar cálculo variacional a la misma.[3]​ Si se considera la clase de todas las trayectorias regulares desde un puntoSe utilizan coordenadas esféricas de forma tal queToda curva sobre la esfera que no interseca alguno de los polos, excepto posiblemente los puntos finales, se puede parametrizar mediante si se le permite aLos círculos máximos también se utilizan como aproximaciones bastante precisas de las geodésicas en la superficie de la Tierra para la navegación aérea o marítima (aunque la Tierra no es una esfera perfecta), así como en los cuerpos celestes esferoidales.Otro gran círculo es el que divide los hemisferios terrestre y acuático.Un pequeño arco de círculo grande entre dos puntos es el camino superficial más corto entre ellos.En este sentido, el arco pequeño es análogo a las "líneas rectas" de la geometría euclídea.