Paralelismo (matemática)
En geometría, el paralelismo es una relación que se establece entre cualquier variedad lineal de dimensión mayor o igual a 1 (rectas, planos, hiperplanos, entre otros).
En geometría afín, expresando una variedad lineal como V = p + E, con p punto y E espacio vectorial, se dice que A = a + F es paralela a B = b + G si y solo si F está contenido en G o G está contenido en F, donde A y B son subvariedades lineales de la misma variedad lineal V y F y G son subespacios vectoriales del mismo espacio vectorial E.
), esto se traduce de la siguiente manera: dos rectas son paralelas si contienen un mismo vector director.
Obsérvese que, en un espacio afín tridimensional, una recta y un plano pueden ser paralelos, y también que la coincidencia de variedades lineales es un caso particular de paralelismo.
Dadas las rectas paralelas l y m en el espacio euclídeo, las siguientes propiedades son equivalentes: Dado que se trata de propiedades equivalentes, cualquiera de ellas podría tomarse como definición de rectas paralelas en el espacio euclídeo, pero la primera y la tercera propiedad implican medición, y por tanto, son "más complicadas" que la segunda.
Simplicio también menciona la definición de Posidonio así como su modificación por el filósofo Aganis.
Wilson (1868, p. 12) Augustus De Morgan revisó este texto y lo declaró un fracaso, principalmente sobre la base de esta definición y la forma en que Wilson la utilizó para demostrar cosas sobre las líneas paralelas.
La principal dificultad, como señaló Dodgson, era que para utilizarlas de este modo era necesario añadir axiomas adicionales al sistema.
El mismo símbolo se utiliza para una función binaria en ingeniería eléctrica (el operador paralelo).
), así como del operador lógico o (||) en varios lenguajes de programación.
Estas mismas propiedades se pueden comprobar en el conjunto de planos paralelos en el espacio.
Resolver los sistemas lineales y para obtener las coordenadas de los puntos.
Las soluciones de los sistemas lineales son los puntos y Estas fórmulas siguen dando las coordenadas correctas de los puntos aunque las rectas paralelas sean horizontales (es decir, m = 0).
Una recta m y un plano q en el espacio tridimensional, la recta no situada en ese plano, son paralelos si y sólo si no se intersecan.
Equivalentemente, son paralelas si y sólo si la distancia desde un punto P en la recta m al punto más cercano en el plano q es independiente de la posición de P en la recta m. De forma similar al hecho de que las rectas paralelas deben estar situadas en el mismo plano, los planos paralelos deben estar situados en el mismo espacio tridimensional y no contener ningún punto en común.
Esto nunca se cumple si los dos planos no están en el mismo espacio tridimensional.
En física puede interpretarse como el camino que sigue una partícula si no se le aplica ninguna fuerza.
En geometría general las tres propiedades anteriores dan tres tipos diferentes de curvas, curvas equidistantes, geodésicas paralelas y geodésicas que comparten una perpendicular común, respectivamente.
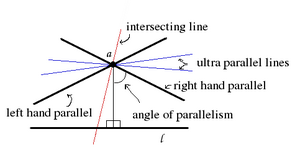
Como en la ilustración a través de un punto a que no está en la línea l hay dos paralelas límite, una por cada dirección punto ideal de la línea l. Separan las líneas que se intersecan con la línea l y las que son ultra paralelas a la línea l. Las rectas ultra paralelas tienen una única perpendicular común (teorema de la ultraparalela), y divergen a ambos lados de esta perpendicular común.
Sin embargo, en el caso l = n, las rectas superpuestas no se consideran paralelas en geometría euclídea.