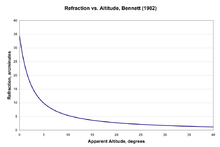
Refracción atmosférica
El aire turbulento puede hacer que los objetos distantes parezcan centellear o brillar.
La refracción atmosférica se considera al medir la posición de los objetos celestes y terrestres.
A veces el Efecto Nueva Zembla, "la refracción horizontal puede superar los dos grados".
Es menor que la astronómica y apenas perceptible a simple vista, unos pocos segundos de arco o menos, pero " es enorme en comparación con los errores de medición en la topografía".
El efecto de la refracción R sobre la altura de un astro hace que la altura aparente sea mayor que la real, eleva al astro, de modo que se dará la relación: hreal = haparente - R. Una fórmula rápida para una altitud superior a unos 20 grados asumiendo una refracción "estándar" es:[3]
Esto puede hacer que los objetos astronómicos aparezcan dispersos en un espectro en imágenes de alta resolución.
Asimismo, los navegantes no apuntan con un sextante una estrella por debajo de los 20° sobre el horizonte.
Si no se pueden evitar las observaciones de objetos cerca del horizonte, es posible equipar un telescopio óptico con sistemas de control para compensar el cambio causado por la refracción.
La refracción atmosférica se vuelve más severa cuando los gradientes de temperatura son fuertes, y la refracción no es uniforme cuando la atmósfera es heterogénea, como cuando ocurre turbulencia en el aire.
Si la atmósfera desapareciera repentinamente en este momento, uno no podría ver el sol, ya que estaría completamente debajo del horizonte.
En el caso de la Luna, se necesitan correcciones adicionales para el paralaje horizontal de la Luna y su semidiámetro aparente; ambos varían con la distancia Tierra-Luna.
Los cálculos más precisos pueden ser útiles para determinar los cambios diarios en los tiempos de subida y puesta que ocurrirían con el valor estándar de refracción[note 1] si se entiende que los cambios reales pueden diferir debido a variaciones impredecibles en la refracción.
[6] Young[10][14] distinguió varias regiones en las que se aplicaban diferentes métodos para calcular la refracción astronómica.
Como señala The Nautical Almanac, "los valores reales de... la refracción a bajas altitudes pueden, en condiciones atmosféricas extremas, diferir considerablemente de los valores medios utilizados en las tablas".
George Comstock desarrolló una primera aproximación simple de esta forma, que incorporaba directamente la temperatura y la presión en el observador:[21] donde R es la refracción en segundos de arco, b es la presión atmosférica en milímetros de mercurio y t es la temperatura en Celsius.
Se ha supuesto en la fórmula que las condiciones de presión atmosférica y temperatura son los estándares y que la longitud de onda corresponde a la más sensible para el ojo humano.
Durante mucho tiempo, los grandes telescopios profesionales han tenido un corrector de ajuste variable en la trayectoria del haz, con el que se pueden corregir los efectos de la dispersión atmosférica en función de la altitud y se puede mantener la resolución del telescopio incluso cuando se registra en todo el rango espectral accesible.
Desde hace un tiempo también existen correctores más o menos complejos para telescopios de aficionados, los llamados “Compensadores de Dispersión Atmosférica” o “Atmospheric Dispersion Compensator” en inglés, abreviado ADC.
Los componentes más lentos de estas fluctuaciones son visibles como parpadeo (también llamado centelleo).
Estos efectos no son visibles a simple vista, pero pueden verse fácilmente incluso con telescopios pequeños.
[38] Como aproximación común, la refracción terrestre se considera como una curvatura constante del rayo de luz o línea de visión, en la que se puede considerar que el rayo describe una trayectoria circular.
La versión más grande del coeficiente k, que mide la relación entre el radio de la Tierra y el radio de la línea de visión, viene dada por:[39] donde la temperatura T se da en kelvins, la presión P en milibares y la altura h en metros.
Aunque la línea recta desde su ojo hasta una montaña distante puede estar bloqueada por una colina más cercana, el rayo puede curvarse lo suficiente como para hacer visible el pico distante.
Según este modelo, el rayo puede considerarse una línea recta en una Tierra de radio aumentado.
La curvatura del rayo refractado en segundos de arco por metro se puede calcular usando la relación[41] donde 1/σ es la curvatura del rayo en segundos de arco por metro, P es la presión en milibares, T es la temperatura en kelvins y β es el ángulo del rayo con la horizontal.