Geoide

Se denomina geoide (griego γεια gueia, ‘tierra’, y ειδος eidos, ‘forma’, ‘apariencia’ —por lo que significaría ‘forma que tiene la Tierra’—) al cuerpo definido por la superficie equipotencial del campo de gravedad terrestre.

Esta superficie se extiende a través de los continentes (como con hipotéticos canales muy estrechos).

[1]​ Solo se puede conocer a través de extensas mediciones y cálculos gravitacionales.

A pesar de ser un concepto importante durante casi 200 años en la historia de la geodesia y la geofísica, se ha definido con alta precisión solo desde los avances en la geodesia satelital a fines del siglo XX.

Esta noción de la Tierra como geoide fue predicha por Isaac Newton en sus Principia durante el año 1687.

Para ello Newton se valió de un sencillo experimento: hacer girar velozmente un cuerpo viscoso en un fluido líquido.

En geografía y disciplinas afines o derivadas (geodesia, cartografía, topografía, etc.) actualmente un geoide es la superficie física definida mediante el potencial gravitatorio, de modo que sobre él hay en todos los puntos la misma atracción terrestre.

Gráficamente se puede definir como la superficie de los mares en calma prolongada bajo los continentes.

Si las masas de tierra continental estuvieran atravesadas por una serie de túneles o canales, el nivel del mar en esos canales también coincidiría casi con el geoide.

Eso significa que cuando se viaja en barco, uno no nota las ondulaciones del geoide ; la vertical local (plomada) siempre es perpendicular al geoide y el horizonte local es tangencial a este.

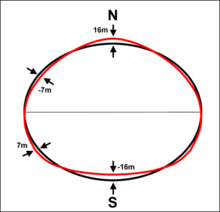
Un esferoide oblato se usa típicamente como la tierra idealizada, pero incluso si la tierra fuera esférica y no rotara, la fuerza de la gravedad no sería la misma en todas partes porque la densidad varía en todo el planeta.

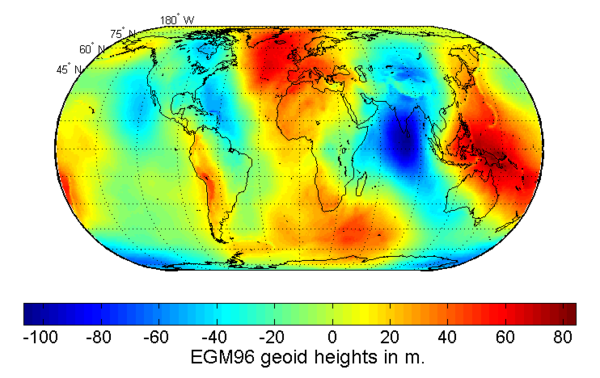
Los receptores GPS modernos tienen una cuadrícula implementada en su software mediante la cual obtienen, a partir de la posición actual, la altura del geoide (por ejemplo, el geoide EGM-96) sobre el Sistema Geodésico Mundial (WGS) elipsoide.

Cuando la altura no es cero en un barco, la discrepancia se debe a otros factores, como las mareas oceánicas, la presión atmosférica (efectos meteorológicos), la topografía local de la superficie del mar y las incertidumbres de medición.

[4]​ Esta relación puede entenderse recordando que el potencial de gravedad se define de modo que tenga valores negativos y sea inversamente proporcional a la distancia del cuerpo.

Como consecuencia, la superficie equipotencial que define el geoide se encontrará desplazada lejos del exceso de masa.

[5]​ La mayor desviación absoluta se puede encontrar en el "bajo geoide del Océano Índico".

Cálculos sintéticos muestran que la firma geoidal de una corteza engrosada (por ejemplo, en cinturones orogénicos producidos por colisión continental) es positiva, al contrario de lo que cabría esperar si el engrosamiento afecta a toda la litosfera.

[12]​[13]​[14]​[15]​ Las ondulaciones del geoide muestran incertidumbres que se pueden estimar utilizando varios métodos, por ejemplo, colocación de mínimos cuadrados (LSC), lógica difusa, redes neutrales artificiales, funciones de base radial (RBF) y técnicas geoestadísticas.

El enfoque geoestadístico se ha definido como la técnica más mejorada en la predicción de la ondulación del geoide.

[16]​ Misiones satelitales recientes, como Gravity field and steady-state Ocean Circulation Explorer (GOCE) y Gravity Recovery and Climate Experiment (GRACE), han permitido el estudio de señales de geoide variables en el tiempo.

Los armónicos esféricos se utilizan a menudo para aproximar la forma del geoide.

son los coeficientes numéricos del modelo basados en los datos medidos.Tenga en cuenta que la ecuación anterior describe el potencial gravitatorio de la Tierra

El geoide es una superficie equipotencial particular,[18]​ y es algo complicado de calcular.

Por tanto, hay (2n+1) coeficientes para cada valor de n. Usando estos hechos y la fórmula,

, se deduce que el número total de coeficientes está dado por

Para definir el geoide, se adopta arbitrariamente el valor de potencial cuyo geoide asociado se aproxima más a la superficie de los océanos (la superficie media del mar, prescindiendo del oleaje, las mareas, las corrientes y la rotación terrestre, coincide casi exactamente con una superficie equipotencial).

La forma del geoide no coincide necesariamente con la topografía terrestre, modelada por fuerzas endógenas (tectónica de placas) y exógenas (agentes geomorfológicos).

Algunos geofísicos consideran al esferoide como modelo geométrico de la tierra y no solo a este sino también a la esfera, por ello el esferoide tiene meridiana principal y ecuador.

Por consiguiente el geoide se utiliza principalmente para referenciar las cotas de nivel.

Tal conocimiento es aún imposible sin una cierta aproximación que deja importante margen de error, resultando así poco operativa desde el punto de vista matemático la definición del geoide.