Espacio tridimensional

Modelo geométrico del espacio físico.

Una representación de un sistema de coordenadas cartesiano tridimensional con el eje x apuntando hacia el observador.

En geometría , un espacio tridimensional ( espacio 3D , espacio tridimensional o, raramente, espacio tridimensional ) es un espacio matemático en el que se requieren tres valores ( coordenadas ) para determinar la posición de un punto . Lo más común es que sea el espacio euclidiano tridimensional , es decir, el espacio euclidiano de dimensión tres, el que modela el espacio físico . Los espacios tridimensionales más generales se denominan 3 variedades . El término también puede referirse coloquialmente a un subconjunto del espacio, una región tridimensional (o dominio 3D ), ^[1] una figura sólida .

Técnicamente, una tupla de n números puede entenderse como las coordenadas cartesianas de una ubicación en un espacio euclidiano de n dimensiones. El conjunto de estas n -tuplas se denota comúnmente y puede identificarse como el par formado por un espacio euclidiano de n dimensiones y un sistema de coordenadas cartesiano . Cuando n = 3 , este espacio se llama ${\displaystyle \mathbb {R} ^{n},}$espacio euclidiano tridimensional (o simplemente "espacio euclidiano" cuando el contexto es claro). ^[2] En la física clásica , sirve como modelo del universo físico , en el que existe toda la materia conocida . Cuando se considera la teoría de la relatividad , se puede considerar un subespacio local del espacio-tiempo . ^[3] Si bien este espacio sigue siendo la forma más convincente y útil de modelar el mundo tal como se experimenta, ^[4] es solo un ejemplo de una gran variedad de espacios en tres dimensiones llamados 3 variedades . En este ejemplo clásico, cuando los tres valores se refieren a mediciones en diferentes direcciones ( coordenadas ), se pueden elegir tres direcciones cualesquiera, siempre que estas direcciones no se encuentren en el mismo plano . Además, si estas direcciones son perpendiculares por pares , los tres valores a menudo se etiquetan con los términos ancho /ancho , alto /profundidad y largo .

Historia

Los libros XI a XIII de los Elementos de Euclides trataban de la geometría tridimensional. El Libro XI desarrolla nociones de ortogonalidad y paralelismo de líneas y planos, y define sólidos, incluidos paralelepípedos, pirámides, prismas, esferas, octaedros, icosaedros y dodecaedros. El libro XII desarrolla nociones de semejanza de sólidos. El Libro XIII describe la construcción de los cinco sólidos platónicos regulares en una esfera.

En el siglo XVII, el espacio tridimensional se describía con coordenadas cartesianas , con el advenimiento de la geometría analítica desarrollada por René Descartes en su obra La Géométrie y Pierre de Fermat en el manuscrito Ad locos planos et solidos isagoge (Introducción a los lugares planos y sólidos). ), que no fue publicado durante la vida de Fermat. Sin embargo, sólo la obra de Fermat trataba del espacio tridimensional.

En el siglo XIX, los desarrollos de la geometría del espacio tridimensional llegaron con el desarrollo de los cuaterniones por parte de William Rowan Hamilton . De hecho, fue Hamilton quien acuñó los términos escalar y vector , y fueron definidos por primera vez dentro de su marco geométrico para los cuaterniones . El espacio tridimensional podría entonces describirse mediante cuaterniones que tuvieran un componente escalar evanescente, es decir ,. Si bien Hamilton no lo estudió explícitamente, esto introdujo indirectamente nociones de base, aquí dadas por los elementos cuaternión , así como el producto escalar y el producto cruz , que corresponden a (el negativo de) la parte escalar y la parte vectorial del producto de dos cuaterniones vectoriales. ${\displaystyle q=a+ui+vj+wk}$ ${\displaystyle a=0}$ ${\displaystyle i,j,k}$

No fue hasta Josiah Willard Gibbs que estos dos productos se identificaron por derecho propio, y la notación moderna para el producto punto y cruz se introdujo en sus notas didácticas en el aula, que también se encuentran en el libro de texto de 1901 Análisis vectorial escrito por Edwin Bidwell Wilson con base en sobre las conferencias de Gibbs.

También durante el siglo XIX se produjeron avances en el formalismo abstracto de los espacios vectoriales, con el trabajo de Hermann Grassmann y Giuseppe Peano , este último fue el primero en dar la definición moderna de espacios vectoriales como una estructura algebraica.

En geometría euclidiana

Sistemas coordinados

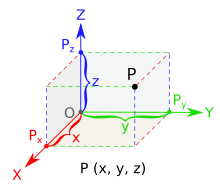
En matemáticas, la geometría analítica (también llamada geometría cartesiana) describe cada punto del espacio tridimensional mediante tres coordenadas. Se dan tres ejes de coordenadas , cada uno perpendicular a los otros dos en el origen , el punto en el que se cruzan. Por lo general, están etiquetados como x , y y z . En relación con estos ejes, la posición de cualquier punto en el espacio tridimensional está dada por un triple ordenado de números reales , cada número da la distancia de ese punto desde el origen medida a lo largo del eje dado, que es igual a la distancia de ese punto del plano determinado por los otros dos ejes. ^[5]

Otros métodos populares para describir la ubicación de un punto en el espacio tridimensional incluyen coordenadas cilíndricas y coordenadas esféricas , aunque existe un número infinito de métodos posibles. Para más información, véase Espacio euclidiano .

A continuación se muestran imágenes de los sistemas mencionados anteriormente.

• 
  sistema de coordenadas Cartesianas
• 
  Sistema de coordenadas cilíndrico
• 
  Sistema de coordenadas esféricas

lineas y planos

Dos puntos distintos siempre determinan una línea (recta) . Tres puntos distintos son colineales o determinan un plano único . Por otro lado, cuatro puntos distintos pueden ser colineales, coplanares o determinar todo el espacio.

Dos líneas distintas pueden cruzarse, ser paralelas o estar sesgadas . Dos líneas paralelas, o dos líneas que se cruzan , se encuentran en un plano único, por lo que las líneas oblicuas son líneas que no se encuentran ni se encuentran en un plano común.

Dos planos distintos pueden encontrarse en una línea común o ser paralelos (es decir, no encontrarse). Tres planos distintos, de los cuales ningún par es paralelo, pueden encontrarse en una línea común, encontrarse en un único punto común o no tener ningún punto en común. En el último caso, las tres líneas de intersección de cada par de planos son mutuamente paralelas.

Una línea puede estar en un plano determinado, intersecar ese plano en un único punto o ser paralela al plano. En el último caso, habrá rectas en el plano paralelas a la recta dada.

Un hiperplano es un subespacio de una dimensión menor que la dimensión del espacio completo. Los hiperplanos de un espacio tridimensional son los subespacios bidimensionales, es decir, los planos. En términos de coordenadas cartesianas, los puntos de un hiperplano satisfacen una única ecuación lineal , por lo que los planos en este espacio tridimensional se describen mediante ecuaciones lineales. Una línea puede describirse mediante un par de ecuaciones lineales independientes, cada una de las cuales representa un plano que tiene esta línea como intersección común.

El teorema de Varignon establece que los puntos medios de cualquier cuadrilátero en ℝ ³ forman un paralelogramo y, por tanto, son coplanares.

Esferas y bolas

Una proyección en perspectiva de una esfera en dos dimensiones.

Una esfera en el espacio tridimensional (también llamada 2 esferas porque es un objeto bidimensional) consta del conjunto de todos los puntos en el espacio tridimensional a una distancia fija r de un punto central P. El sólido encerrado por la esfera se llama bola (o, más precisamente, 3 bolas ).

El volumen de la pelota está dado por

$${\displaystyle V={\frac {4}{3}}\pi r^{3},}$$

$${\displaystyle A=4\pi r^{2}.}$$

3 esferasR ⁴P ( x , y , z , w )x ² + y ² + z ² + w ² = 1

Esta 3 esferas es un ejemplo de una variedad 3: un espacio que "parece localmente" como un espacio tridimensional. En términos topológicos precisos, cada punto de la 3-esfera tiene una vecindad que es homeomorfa a un subconjunto abierto del espacio 3-D.

Politopos

En tres dimensiones, existen nueve politopos regulares: los cinco sólidos platónicos convexos y los cuatro poliedros no convexos de Kepler-Poinsot .

Superficies de revolución

Una superficie generada al hacer girar una curva plana alrededor de una línea fija en su plano como eje se llama superficie de revolución . La curva plana se llama generatriz de la superficie. Una sección de la superficie, hecha al intersectar la superficie con un plano que es perpendicular (ortogonal) al eje, es un círculo.

Ejemplos simples ocurren cuando la generatriz es una línea. Si la línea generatriz cruza la línea del eje, la superficie de revolución es un cono circular recto con el vértice (ápice) como punto de intersección. Sin embargo, si la generatriz y el eje son paralelos, entonces la superficie de revolución es un cilindro circular .

Superficies cuádricas

En analogía con las secciones cónicas , el conjunto de puntos cuyas coordenadas cartesianas satisfacen la ecuación general de segundo grado, a saber,

$${\displaystyle Ax^{2}+By^{2}+Cz^{2}+Fxy+Gyz+Hxz+Jx+Ky+Lz+M=0,}$$

A , B , C , F , G , H , J , K , LMA , B , C , F , GHsuperficie cuádrica^[6]

Hay seis tipos de superficies cuádricas no degeneradas :

1. elipsoide
2. Hiperboloide de una hoja.
3. Hiperboloide de dos hojas.
4. Cono elíptico
5. paraboloide elíptico
6. paraboloide hiperbólico

Las superficies cuádricas degeneradas son el conjunto vacío, un solo punto, una sola recta, un solo plano, un par de planos o un cilindro cuadrático (superficie formada por una sección cónica no degenerada en un plano π y todas las rectas de R ³ a través de esa cónica que son normales a π ). ^[6] Los conos elípticos a veces también se consideran superficies cuádricas degeneradas.

Tanto el hiperboloide de una hoja como el paraboloide hiperbólico son superficies regladas , lo que significa que pueden estar formadas por una familia de líneas rectas. De hecho, cada uno tiene dos familias de líneas generadoras, los miembros de cada familia están separados y cada miembro de una familia se cruza, con una sola excepción, cada miembro de la otra familia. ^[7] Cada familia se llama regulus .

En álgebra lineal

Otra forma de ver el espacio tridimensional se encuentra en el álgebra lineal , donde la idea de independencia es crucial. El espacio tiene tres dimensiones porque el largo de una caja es independiente de su ancho o ancho. En el lenguaje técnico del álgebra lineal, el espacio es tridimensional porque cada punto del espacio puede describirse mediante una combinación lineal de tres vectores independientes .

Producto escalar, ángulo y longitud

Un vector se puede representar como una flecha. La magnitud del vector es su longitud y su dirección es la dirección que apunta la flecha. Un vector en ℝ ³ se puede representar mediante un triple ordenado de números reales. Estos números se llaman componentes del vector.

El producto escalar de dos vectores A = [ A ₁ , A ₂ , A ₃ ] y B = [ B ₁ , B ₂ , B ₃ ] se define como: ^[8]

${\displaystyle \mathbf {A} \cdot \mathbf {B} =A_{1}B_{1}+A_{2}B_{2}+A_{3}B_{3}=\sum _{i=1}^{3}A_{i}B_{i}.}$

La magnitud de un vector A se denota por || Un || . El producto escalar de un vector A = [ A ₁ , A ₂ , A ₃ ] consigo mismo es

${\displaystyle \mathbf {A} \cdot \mathbf {A} =\|\mathbf {A} \|^{2}=A_{1}^{2}+A_{2}^{2}+A_{3}^{2},}$

lo que da

${\displaystyle \|\mathbf {A} \|={\sqrt {\mathbf {A} \cdot \mathbf {A} }}={\sqrt {A_{1}^{2}+A_{2}^{2}+A_{3}^{2}}},}$

la fórmula para la longitud euclidiana del vector.

Sin referencia a los componentes de los vectores, el producto escalar de dos vectores euclidianos A y B distintos de cero viene dado por ^[9]

${\displaystyle \mathbf {A} \cdot \mathbf {B} =\|\mathbf {A} \|\,\|\mathbf {B} \|\cos \theta ,}$

donde θ es el ángulo entre A y B.

Producto cruzado

El producto vectorial o producto vectorial es una operación binaria sobre dos vectores en un espacio tridimensional y se denota con el símbolo ×. El producto vectorial A × B de los vectores A y B es un vector perpendicular a ambos y, por tanto, normal al plano que los contiene. Tiene muchas aplicaciones en matemáticas, física e ingeniería .

En lenguaje de funciones, el producto cruzado es una función . ${\displaystyle \times :\mathbb {R} ^{3}\times \mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}}$

Los componentes del producto vectorial son , y también se pueden escribir en componentes, utilizando la convención de suma de Einstein, como dónde está el símbolo de Levi-Civita . Tiene la propiedad de que . ${\displaystyle \mathbf {A} \times \mathbf {B} =[A_{2}B_{3}-B_{2}A_{3},A_{3}B_{1}-B_{3}A_{1},A_{1}B_{2}-B_{1}A_{2}]}$ ${\displaystyle (\mathbf {A} \times \mathbf {B} )_{i}=\varepsilon _{ijk}A_{j}B_{k}}$ ${\displaystyle \varepsilon _{ijk}}$ ${\displaystyle \mathbf {A} \times \mathbf {B} =-\mathbf {B} \times \mathbf {A} }$

Su magnitud está relacionada con el ángulo entre y por la identidad ${\displaystyle \theta }$ ${\displaystyle \mathbf {A} }$ ${\displaystyle \mathbf {B} }$

$${\displaystyle \left\|\mathbf {A} \times \mathbf {B} \right\|=\left\|\mathbf {A} \right\|\cdot \left\|\mathbf {B} \right\|\cdot \left|\sin \theta \right|.}$$

El espacio y el producto forman un álgebra sobre un campo , que no es conmutativo ni asociativo , sino que es un álgebra de Lie cuyo producto vectorial es el corchete de Lie. Específicamente, el espacio junto con el producto, es isomorfo al álgebra de Lie de rotaciones tridimensionales, denotado . Para satisfacer los axiomas de un álgebra de Lie, en lugar de asociatividad, el producto cruz satisface la identidad de Jacobi . Para tres vectores cualesquiera y ${\displaystyle (\mathbb {R} ^{3},\times )}$ ${\displaystyle {\mathfrak {so}}(3)}$ ${\displaystyle \mathbf {A} ,\mathbf {B} }$ ${\displaystyle \mathbf {C} }$

$${\displaystyle \mathbf {A} \times (\mathbf {B} \times \mathbf {C} )+\mathbf {B} \times (\mathbf {C} \times \mathbf {A} )+\mathbf {C} \times (\mathbf {A} \times \mathbf {B} )=0}$$

Se puede en n dimensiones tomar el producto de n − 1 vectores para producir un vector perpendicular a todos ellos. Pero si el producto se limita a productos binarios no triviales con resultados vectoriales, existe sólo en tres y siete dimensiones . ^[10]

El producto cruzado con respecto a un sistema de coordenadas diestro

Descripción abstracta

Puede resultar útil describir el espacio tridimensional como un espacio vectorial tridimensional sobre números reales. Esto difiere de una manera sutil. Por definición, existe una base para . Esto corresponde a un isomorfismo entre y : la construcción del isomorfismo se encuentra aquí . Sin embargo, no existe una base "preferida" o "canónica" para . ${\displaystyle V}$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle {\mathcal {B}}=\{e_{1},e_{2},e_{3}\}}$ ${\displaystyle V}$ ${\displaystyle V}$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle V}$

Por otro lado, existe una base preferida para , que se debe a su descripción como producto cartesiano de copias de , es decir, . Esto permite la definición de proyecciones canónicas, , donde . Por ejemplo, . Esto permite entonces la definición de la base estándar definida por ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} ^{3}=\mathbb {R} \times \mathbb {R} \times \mathbb {R} }$ ${\displaystyle \pi _{i}:\mathbb {R} ^{3}\rightarrow \mathbb {R} }$ ${\displaystyle 1\leq i\leq 3}$ ${\displaystyle \pi _{1}(x_{1},x_{2},x_{3})=x}$ ${\displaystyle {\mathcal {B}}_{\text{Standard}}=\{E_{1},E_{2},E_{3}\}}$

$${\displaystyle \pi _{i}(E_{j})=\delta _{ij}}$$

delta del Kronecker ${\displaystyle \delta _{ij}}$

$${\displaystyle E_{1}={\begin{pmatrix}1\\0\\0\end{pmatrix}},E_{2}={\begin{pmatrix}0\\1\\0\end{pmatrix}},E_{3}={\begin{pmatrix}0\\0\\1\end{pmatrix}}.}$$

Por lo tanto, puede verse como el espacio vectorial abstracto, junto con la estructura adicional de una elección de base. Por el contrario, se puede obtener comenzando y "olvidando" la estructura del producto cartesiano o, de manera equivalente, la elección estándar de base. ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle V}$ ${\displaystyle \mathbb {R} ^{3}}$

A diferencia de un espacio vectorial general , el espacio a veces se denomina espacio de coordenadas. ^[11] ${\displaystyle V}$ ${\displaystyle \mathbb {R} ^{3}}$

Físicamente, es conceptualmente deseable utilizar el formalismo abstracto para asumir la menor estructura posible si no está dada por los parámetros de un problema particular. Por ejemplo, en un problema de simetría rotacional, trabajar con la descripción más concreta del espacio tridimensional supone una elección de base, correspondiente a un conjunto de ejes. Pero en simetría rotacional, no hay ninguna razón por la que se prefiera un conjunto de ejes al mismo conjunto de ejes que se ha girado arbitrariamente. Dicho de otra manera, una elección preferida de ejes rompe la simetría rotacional del espacio físico. ${\displaystyle \mathbb {R} ^{3}}$

Computacionalmente, es necesario trabajar con la descripción más concreta para poder realizar cálculos concretos. ${\displaystyle \mathbb {R} ^{3}}$

Descripción afín

Una descripción aún más abstracta consiste en modelar el espacio físico como un espacio afín tridimensional sobre los números reales. Esto es único hasta el isomorfismo afín. A veces se le denomina espacio euclidiano tridimensional. Así como la descripción del espacio vectorial proviene de "olvidar la base preferida" de , la descripción del espacio afín proviene de "olvidar el origen" del espacio vectorial. Los espacios euclidianos a veces se denominan espacios afines euclidianos para distinguirlos de los espacios vectoriales euclidianos. ^[12] ${\displaystyle E(3)}$ ${\displaystyle \mathbb {R} ^{3}}$

Esto es físicamente atractivo ya que pone de manifiesto la invariancia de traducción del espacio físico. Un origen preferido rompe la invariancia traslacional.

Espacio interior del producto

La discusión anterior no involucra el producto escalar . El producto escalar es un ejemplo de producto interno . El espacio físico se puede modelar como un espacio vectorial que además tiene la estructura de un producto interno. El producto interior define nociones de longitud y ángulo (y por tanto, en particular, la noción de ortogonalidad). Para cualquier producto interno, existen bases bajo las cuales el producto interno concuerda con el producto escalar, pero nuevamente, hay muchas bases posibles diferentes, ninguna de las cuales es la preferida. Se diferencian entre sí por una rotación, un elemento del grupo de rotaciones SO(3) .

en calculo

Degradado, divergencia y rizo.

En un sistema de coordenadas rectangular, el gradiente de una función (diferenciable) viene dado por ${\displaystyle f:\mathbb {R} ^{3}\rightarrow \mathbb {R} }$

${\displaystyle \nabla f={\frac {\partial f}{\partial x}}\mathbf {i} +{\frac {\partial f}{\partial y}}\mathbf {j} +{\frac {\partial f}{\partial z}}\mathbf {k} }$

y en notación índice se escribe

$${\displaystyle (\nabla f)_{i}=\partial _{i}f.}$$

La divergencia de un campo vectorial (diferenciable) F = U i + V j + W k , es decir, una función , es igual a la función escalar : ${\displaystyle \mathbf {F} :\mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}}$

${\displaystyle \operatorname {div} \,\mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {\partial U}{\partial x}}+{\frac {\partial V}{\partial y}}+{\frac {\partial W}{\partial z}}.}$

En notación de índice, con la convención de suma de Einstein, esto es

$${\displaystyle \nabla \cdot \mathbf {F} =\partial _{i}F_{i}.}$$

Expandido en coordenadas cartesianas (ver Del en coordenadas cilíndricas y esféricas para representaciones de coordenadas esféricas y cilíndricas ), el rizo ∇ × F es, para F, compuesto por [ F _x , F _y , F _z ]:

${\displaystyle {\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\\\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\\\F_{x}&F_{y}&F_{z}\end{vmatrix}}}$

donde i , j y k son los vectores unitarios para los ejes x , y y z , respectivamente. Esto se expande de la siguiente manera: ^[13]

${\displaystyle \left({\frac {\partial F_{z}}{\partial y}}-{\frac {\partial F_{y}}{\partial z}}\right)\mathbf {i} +\left({\frac {\partial F_{x}}{\partial z}}-{\frac {\partial F_{z}}{\partial x}}\right)\mathbf {j} +\left({\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{x}}{\partial y}}\right)\mathbf {k} .}$

En notación de índice, con la convención de suma de Einstein, esto es

$${\displaystyle (\nabla \times \mathbf {F} )_{i}=\epsilon _{ijk}\partial _{j}F_{k},}$$

símbolo de Levi-Civita ${\displaystyle \epsilon _{ijk}}$

Integrales de línea, superficie y volumen

Para algún campo escalar f  : U ⊆ R ⁿ → R , la integral de línea a lo largo de una curva suave por tramos C ⊂ U se define como

${\displaystyle \int \limits _{C}f\,ds=\int _{a}^{b}f(\mathbf {r} (t))|\mathbf {r} '(t)|\,dt.}$

donde r : [a, b] → C es una parametrización biyectiva arbitraria de la curva C tal que r ( a ) y r ( b ) dan los puntos finales de C y . ${\displaystyle a<b}$

Para un campo vectorial F  : U ⊆ R ⁿ → R ⁿ , la integral de línea a lo largo de una curva suave por tramos C ⊂ U , en la dirección de r , se define como

${\displaystyle \int \limits _{C}\mathbf {F} (\mathbf {r} )\cdot \,d\mathbf {r} =\int _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,dt.}$

donde · es el producto escalar y r : [a, b] → C es una parametrización biyectiva de la curva C tal que r ( a ) y r ( b ) dan los puntos finales de C.

Una integral de superficie es una generalización de integrales múltiples para la integración sobre superficies . Puede considerarse como la integral doble análoga de la integral de línea. Para encontrar una fórmula explícita para la integral de superficie, necesitamos parametrizar la superficie de interés, S , considerando un sistema de coordenadas curvilíneas en S , como la latitud y la longitud en una esfera . Sea tal parametrización x ( s , t ), donde ( s , t ) varía en alguna región T del plano . Entonces, la integral de superficie está dada por

${\displaystyle \iint _{S}f\,\mathrm {d} S=\iint _{T}f(\mathbf {x} (s,t))\left\|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right\|\mathrm {d} s\,\mathrm {d} t}$

donde la expresión entre barras del lado derecho es la magnitud del producto cruzado de las derivadas parciales de x ( s , t ), y se conoce como elemento de superficie . Dado un campo vectorial v en S , que es una función que asigna a cada x en S un vector v ( x ), la integral de superficie se puede definir componente por componente de acuerdo con la definición de la integral de superficie de un campo escalar; el resultado es un vector.

Una integral de volumen es una integral sobre un dominio o región tridimensional . Cuando el integrando es trivial (unidad), la integral de volumen es simplemente el volumen de la región . ^{[14] [1]} También puede significar una integral triple dentro de una región D en R ³ de una función y generalmente se escribe como: ${\displaystyle f(x,y,z),}$

${\displaystyle \iiint \limits _{D}f(x,y,z)\,dx\,dy\,dz.}$

Teorema fundamental de las integrales de línea

El teorema fundamental de las integrales de línea dice que una integral de línea a través de un campo gradiente se puede evaluar evaluando el campo escalar original en los puntos finales de la curva.

Dejar . Entonces ${\displaystyle \varphi :U\subseteq \mathbb {R} ^{n}\to \mathbb {R} }$

${\displaystyle \varphi \left(\mathbf {q} \right)-\varphi \left(\mathbf {p} \right)=\int _{\gamma [\mathbf {p} ,\,\mathbf {q} ]}\nabla \varphi (\mathbf {r} )\cdot d\mathbf {r} .}$

teorema de stokes

El teorema de Stokes relaciona la integral de superficie de la curvatura de un campo vectorial F sobre una superficie Σ en el espacio tridimensional euclidiano con la integral de línea del campo vectorial sobre su límite ∂Σ:

${\displaystyle \iint _{\Sigma }\nabla \times \mathbf {F} \cdot \mathrm {d} \mathbf {\Sigma } =\oint _{\partial \Sigma }\mathbf {F} \cdot \mathrm {d} \mathbf {r} .}$

Teorema de divergencia

Supongamos que V es un subconjunto de (en el caso de n = 3, V representa un volumen en el espacio 3D) que es compacto y tiene un límite suave por partes S (también indicado con ∂ V = S ). Si F es un campo vectorial continuamente diferenciable definido en una vecindad de V , entonces el teorema de la divergencia dice: ^[15] ${\displaystyle \mathbb {R} ^{n}}$  

${\displaystyle \iiint _{V}\left(\mathbf {\nabla } \cdot \mathbf {F} \right)\,dV=}$ ${\displaystyle \scriptstyle S}$ ${\displaystyle (\mathbf {F} \cdot \mathbf {n} )\,dS.}$

El lado izquierdo es una integral de volumen sobre el volumen V , el lado derecho es la integral de superficie sobre el límite del volumen V. La variedad cerrada ∂ V es generalmente el límite de V orientado por normales que apuntan hacia afuera , y n es el campo normal unitario que apunta hacia afuera del límite ∂ V. ( d S puede usarse como abreviatura de n dS ).

En topología

El logo del globo terráqueo de Wikipedia en 3-D

El espacio tridimensional tiene una serie de propiedades topológicas que lo distinguen de espacios de otros números de dimensión. Por ejemplo, se requieren al menos tres dimensiones para hacer un nudo en un trozo de cuerda. ^[dieciséis]

En geometría diferencial, los espacios tridimensionales genéricos son 3 variedades , que se parecen localmente . ${\displaystyle {\mathbb {R} }^{3}}$

En geometría finita

Muchas ideas de dimensión se pueden probar con geometría finita . El ejemplo más simple es PG(3,2) , que tiene planos de Fano como subespacios bidimensionales. Es un ejemplo de la geometría de Galois , un estudio de la geometría proyectiva utilizando campos finitos . Así, para cualquier campo de Galois GF( q ), existe un espacio proyectivo PG(3, q ) de tres dimensiones. Por ejemplo, tres líneas sesgadas cualesquiera en PG(3, q ) están contenidas exactamente en un regulus . ^[17]

Ver también

• rotación 3D
  • Formalismos de rotación en tres dimensiones.
• Análisis dimensional
• Distancia desde un punto a un plano
• Espacio de cuatro dimensiones
• Líneas sesgadas § Distancia
• Gráfico tridimensional
• Geometria solida

Notas

1. "IEC 60050 - Detalles del IEV número 102-04-39:" dominio tridimensional"". Vocabulario Electrotécnico Internacional (en japonés) . Consultado el 19 de septiembre de 2023 .
2. "Espacio euclidiano - Enciclopedia de Matemáticas". encyclopediaofmath.org . Consultado el 12 de agosto de 2020 .
3. "Detalles del IEV número 113-01-02:" espacio"". Vocabulario Electrotécnico Internacional (en japonés) . Consultado el 7 de noviembre de 2023 .
4. "Espacio euclidiano | geometría". Enciclopedia Británica . Consultado el 12 de agosto de 2020 .
5. Hughes-Hallett, Deborah ; McCallum, William G .; Gleason, Andrew M. (2013). Cálculo: simple y multivariable (6 ed.). John wiley. ISBN 978-0470-88861-2.
6. Brannan, Esplen y Gray 1999, págs.
7. Brannan, Esplen y Gray 1999, págs. 41–42
8. Antón 1994, pag. 133
9. Antón 1994, pag. 131
10. Massey, WS (1983). "Productos cruzados de vectores en espacios euclidianos de dimensiones superiores". El Mensual Matemático Estadounidense . 90 (10): 697–701. doi :10.2307/2323537. JSTOR  2323537. Si se requieren solo tres propiedades básicas del producto vectorial... resulta que un producto vectorial de vectores existe solo en el espacio euclidiano de 3 y 7 dimensiones.
11. Lang 1987, cap. I.1
12. Berger 1987, Capítulo 9.
13. Arfken, pág. 43.
14. "IEC 60050 - Detalles del IEV número 102-04-40:" volumen"". Vocabulario Electrotécnico Internacional (en japonés) . Consultado el 19 de septiembre de 2023 .
15. Señor Spiegel; S. Lipschutz; D. Spellman (2009). Análisis vectorial . Esquemas de Schaum (2ª ed.). Estados Unidos: McGraw Hill. ISBN 978-0-07-161545-7.
16. Rolfsen, Dale (1976). Nudos y Enlaces . Berkeley, California: Publicar o perecer. ISBN 0-914098-16-0.
17. Albrecht Beutelspacher y Ute Rosenbaum (1998) Geometría proyectiva , página 72, Cambridge University Press ISBN 0-521-48277-1 

Referencias

• Anton, Howard (1994), Álgebra lineal elemental (7ª ed.), John Wiley & Sons, ISBN 978-0-471-58742-2
• Arfken, George B. y Hans J. Weber. Métodos matemáticos para físicos , Academic Press; 6ª edición (21 de junio de 2005). ISBN 978-0-12-059876-2 . 
• Berger, Marcel (1987), Geometría I , Berlín: Springer, ISBN 3-540-11658-3
• Brannan, David A.; Esplén, Matthew F.; Gray, Jeremy J. (1999), Geometría , Cambridge University Press, ISBN 978-0-521-59787-6
• Lang, Serge (1987), Álgebra lineal (3.ª ed.), Springer, doi :10.1007/978-1-4757-1949-9, ISBN 978-1-4757-1949-9

enlaces externos

• La definición del diccionario de tridimensional en Wikcionario.
• Weisstein, Eric W. "Geometría cuatridimensional". MundoMatemático .
• Álgebra lineal elemental - Capítulo 8: Geometría tridimensional Keith Matthews de la Universidad de Queensland , 1991